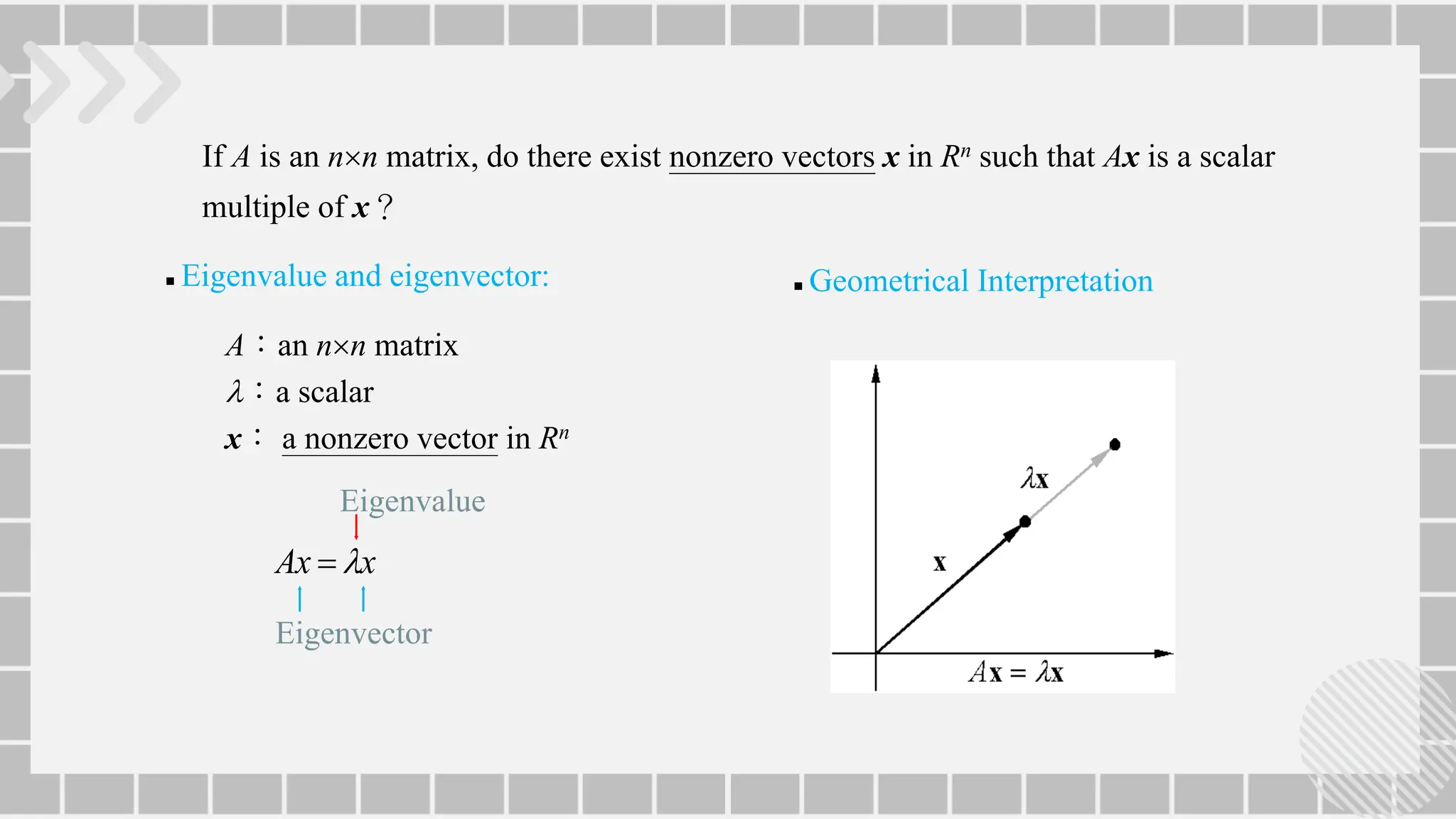
The document discusses eigenvalues and eigenvectors of linear transformations. It defines eigenvalues as scalars that scale eigenvectors by when a linear transformation is applied. Eigenvectors are non-zero vectors that change only in scale and not direction when a linear transformation is applied. The document provides theorems and examples for finding the eigenvalues and eigenvectors of matrices, including finding their characteristic equations and solving homogeneous systems. It determines the dimension of eigenspaces corresponds to eigenvalues.

1. Institute for Excellence in Higher
Education,Bhopal
Sessions:- 2022-2023
Topic:- Eigen values and Eigen vectors of
linear transformation
Submitted To:
Dr.Manoj Ughade Sir
(Professor in Department
of Mathematics,IEHE)
Submitted By:-
Atul(420509) and
Dilpreet Sandhu (420513)
B.Sc(H) Physics III year

2. ACKNOWLEDGEMENT
We (Atul and Dilpreet Sandhu) would like to express my special thanks of gratitude to our teacher (PROF. Manoj
Ughade Sir) who gave me the golden opportunity to do this wonderful assignment on the topic (Eigen values and
Eigen vectors of linear transformation ), which also helped me in doing a lot of Research and I came to know about so
many new things. I am really thankful to him.
Secondly, I would also like to thank my parents and friends who helped me a lot in finalizing this project within the
limited time frame.

3. CERTIFICATE
This is to certify that Atul and Dilpreet Sandhu, a student of B.Sc.(Physics Honours,VI sem) acquaring roll
number – 420509 and 420513 respectively, has successfully completed the assignment of “Mathematics”
on the topic “Eigen values and Eigen vectors of linear transformation” under the guidance of Manoj
Ughade Sir(PROF.of Mathematics department in INSTITUTE FOR EXCELLENCE IN HIGHER
EDUCATION ,BHOPAL).
TEACHER SIGN.
SUBMITTED BY
Atul(420509) and Dilpreet Sandhu(420513)
Date:. 31/03/2023

4. EIGENVALUES &
EIGENVECTORS OF LINEAR
TRANSFORMATIONS.
Eigenvalues and eigenvectors are important concepts in linear algebra that arise when studying linear
transformations.
EIGEN VALUES:-
An eigenvalue of a linear transformation is a scalar that represents how the transformation scales a given
eigenvector. In other words, when the linear transformation is applied to an eigenvector, the resulting vector
is a scalar multiple of the original vector, with the scalar being the eigenvalue.
EIGEN VECTORS:-
An eigenvector of a linear transformation is a non-zero vector that, when multiplied by the transformation,
yields a scalar multiple of itself. In other words, the transformation only changes the scale of the
eigenvector, not its direction.

5. If A is an nn matrix, do there exist nonzero vectors x in Rn such that Ax is a scalar
multiple of x？
 Geometrical Interpretation
 Eigenvalue and eigenvector:
A：an nn matrix
：a scalar
x： a nonzero vector in Rn
x
Ax 

Eigenvalue
Eigenvector

6. •Ex 1: (Verifying eigenvalues and eigenvectors)








1
0
0
2
A 






0
1
1
x 






1
0
2
x
1
1 2
0
1
2
0
2
0
1
1
0
0
2
x
Ax 




























Eigenvalue
Eigenvector
2
2 )
1
(
1
0
1
1
0
1
0
1
0
0
2
x
Ax 































Eigenvalue
Eigenvector

7.  Thm 1: (The eigenspace of A corresponding to )
If A is an nn matrix with an eigenvalue , then the set of all eigenvectors of  together with
the zero vector is a subspace of Rn. This subspace is called the eigenspace of  .
Pf:
x1 and x2 are eigenvectors corresponding to 
)
,
.
.
( 2
2
1
1 x
Ax
x
Ax
e
i 
 

)
to
ing
correspond
r
eigenvecto
an
is
.
.
(
)
(
)
(
)
1
(
2
1
2
1
2
1
2
1
2
1
λ
x
x
e
i
x
x
x
x
Ax
Ax
x
x
A







 


)
to
ing
correspond
r
eigenvecto
an
is
.
.
(
)
(
)
(
)
(
)
(
)
2
(
1
1
1
1
1



cx
e
i
cx
x
c
Ax
c
cx
A 



8.  Mathematical defination for Eigenvalues and eigenvectors of linear
transformations:
.
of
eigenspace
the
called
is
vector)
zero
(with the
of
rs
eigenvecto
all
setof
the
and
,
to
ing
correspond
of
r
eigenvecto
an
called
is
vector
The
.
)
(
such that
vector
nonzero
a
is
there
if
:
n
nsformatio
linear tra
a
of
eigenvalue
an
called
is
number
A





T
T
V
V
T
x
x
x
x 


9. Thm 2: (Finding eigenvalues and eigenvectors of a matrix AMnn )
Let A is an nn matrix.
(2) The eigenvectors of A corresponding to  are the nonzero
solutions of
(1) An eigenvalue of A is a scalar  such that 0
)
I
det( 
 A

0
)
I
( 
 x
A

If has nonzero solutions iff .
0
)
I
( 
 x
A
 0
)
I
det( 
 A

0
)
I
( 


 x
A
x
Ax 

 Note:
(homogeneous system)
 Characteristic polynomial of AMnn:
0
1
1
1
)
I
(
)
I
det( c
c
c
A
A n
n
n







 
 



 
 Characteristic equation of A:
0
)
I
det( 
 A


10. Ex 2 :(Finding eigenvalues and eigenvectors)









5
1
12
2
A
0
)
2
)(
1
(
2
3
5
1
12
2
)
I
det(
2


















 A
Sol: Characteristic equation:
2
,
1 


 
2
,
1
:
s
Eigenvalue 2
1 


 


11. 1
)
1
( 1 


0
,
1
4
4
0
0
4
1
~
4
1
12
3
0
0
4
1
12
3
)
I
(
2
1
2
1
1



























 
































t
t
t
t
x
x
x
x
x
A


2
)
2
( 2 


0
,
1
3
3
0
0
3
1
~
3
1
12
4
0
0
3
1
12
4
)
I
(
2
1
2
1
2



























 
































t
t
t
t
x
x
x
x
x
A


:
Check x
Ax i



12. Ex 3: (Finding eigenvalues and eigenvectors)
Find the eigenvalues and corresponding eigenvectors for the
matrix A. What is the dimension of the eigenspace of each
eigenvalue?









2
0
0
0
2
0
0
1
2
A
Sol: Characteristic equation:
0
)
2
(
2
0
0
0
2
0
0
1
2
I 3








 



 A
Eigenvalue: 2



13. The eigenspace of A corresponding to :
2
































 


0
0
0
0
0
0
0
0
0
0
1
0
)
I
(
3
2
1
x
x
x
x
A

0
,
,
1
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
~
0
0
0
0
0
0
0
1
0
3
2
1
































































 
t
s
t
s
t
s
x
x
x

2
to
ing
correspond
A
of
eigenspace
the
:
,
1
0
0
0
0
1


































R
t
s
t
s
Thus, the dimension of its eigenspace is 2.

14. Notes:
(1) If an eigenvalue 1 occurs as a multiple root (k times) for
the characteristic polynominal, then 1 has multiplicity k.
(2) The multiplicity of an eigenvalue is greater than or equal to
the dimension of its eigenspace.

15. Ex 4：Find the eigenvalues of the matrix A and find a basis
for each of the corresponding eigenspaces.














3
0
0
1
0
2
0
1
10
5
1
0
0
0
0
1
A
Sol: Characteristic equation:
0
)
3
)(
2
(
)
1
(
3
0
0
1
0
2
0
1
10
5
1
0
0
0
0
1
I
2





















 A
3
,
2
,
1
:
s
Eigenvalue 3
2
1 

 



16. 1
)
1
( 1 














































0
0
0
0
2
0
0
1
0
1
0
1
10
5
0
0
0
0
0
0
)
I
(
4
3
2
1
1
x
x
x
x
x
A

0
,
,
1
2
0
2
0
0
1
0
2
2
0
0
0
0
0
0
0
0
2
1
0
0
2
0
0
1
~
2
0
0
1
0
1
0
1
10
5
0
0
0
0
0
0
4
3
2
1



















































































t
s
t
s
t
t
s
t
x
x
x
x
1
2
0
2
,
0
0
1
0






































 is a basis for the eigenspace of A
corresponding to
1



17. 2
)
2
( 2 













































0
0
0
0
1
0
0
1
0
0
0
1
10
5
1
0
0
0
0
1
)
I
(
4
3
2
1
2
x
x
x
x
x
A

0
,
0
1
5
0
0
5
0
0
0
0
0
1
0
0
0
0
5
1
0
0
0
0
1
~
1
0
0
1
0
0
0
1
10
5
1
0
0
0
0
1
4
3
2
1





































































t
t
t
t
x
x
x
x
0
1
5
0


























 is a basis for the eigenspace of A
corresponding to
2



18. 3
)
3
( 3 












































0
0
0
0
0
0
0
1
0
1
0
1
10
5
2
0
0
0
0
2
)
I
(
4
3
2
1
3
x
x
x
x
x
A

0
,
1
0
5
0
0
5
0
0
0
0
0
0
1
0
0
5
0
1
0
0
0
0
1
~
0
0
0
1
0
1
0
1
10
5
2
0
0
0
0
2
4
3
2
1





































































t
t
t
t
x
x
x
x
1
0
5
0



























 is a basis for the eigenspace of A
corresponding to
3



19. Thm 3: (Eigenvalues of triangular matrices)
If A is an nn triangular matrix, then its eigenvalues are the
entries on its main diagonal.
Ex 5: (Finding eigenvalues for diagonal and triangular matrices)













3
3
5
0
1
1
0
0
2
)
( A
a















3
0
0
0
0
0
4
0
0
0
0
0
0
0
0
0
0
0
2
0
0
0
0
0
1
)
( A
b
Sol:
)
3
)(
1
)(
2
(
3
3
5
0
1
1
0
0
2
I
)
( 









 





 A
a
3
,
1
,
2 3
2
1 


 


3
,
4
,
0
,
2
,
1
)
( 5
4
3
2
1 





 




b

20. Ex 6: (Finding eigenvalues and eigenspaces)
.
2
0
0
0
1
3
0
3
1
s
eigenspace
ing
correspond
and
s
eigenvalue
the
Find












A
Sol:
)
4
(
)
2
(
2
0
0
0
1
3
0
3
1
2









 




 A
I
2
,
4
:
s
eigenvalue 2
1 

 

2
for
Basis
)}
1
,
0
,
0
(
),
0
,
1
,
1
{(
4
for
Basis
)}
0
,
1
,
1
{(
follows.
as
are
s
eigenvalue
two
for these
s
eigenspace
The
2
2
1
1








B
B

21. Eigenvalues and eigenvectors have many applications in various fields, including mathematics, physics,
engineering, computer science, and more. Here are some specific examples:
Image and signal processing: Eigenvectors and eigenvalues are used in image and signal processing
techniques, such as Principal Component Analysis (PCA), which is used to reduce the dimensionality of data
sets while retaining as much variance as possible. In this application, the eigenvectors of the covariance
matrix of a set of data points are used as a basis for a new coordinate system that captures the most
important features of the data.
Quantum mechanics: Eigenvectors and eigenvalues are used to represent the state of a quantum system. In
quantum mechanics, the wave function of a particle is an eigenvector of the Hamiltonian operator, and the
corresponding eigenvalue represents the energy of the system.
Structural engineering: Eigenvectors and eigenvalues are used in the analysis of structures, such as bridges
and buildings, to determine their natural frequencies and modes of vibration. This information can be used to
design structures that can withstand external forces, such as wind and earthquakes.
These are just a few examples of the many applications of eigenvectors and eigenvalues. They are powerful
tools that can be used to solve a wide range of problems in various fields.
Applications

22. REFERENCES
ocw.mit.edu
“Matrices & Tensors in Physics” By AW Joshi
REFERENCES 2

23. THANK YOU
Presentation by
Dilpreet Sandhu(420513)
And
Atul(420509).