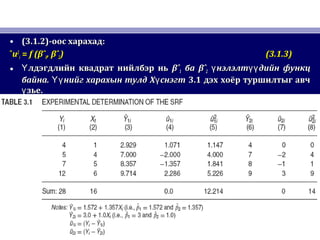
Econ ch 3

1. Бүлэг # 3: ХОС РЕГРЕССИЙН
ЗАГВАР: ҮНЭЛЭЛТИЙН АСУУДАЛ

2. ЭНГИЙН ХАМГИЙН БАГА КВАДРАТЫН АРГА
• Энэ аргыг ойлгохын тулд эхлээдЭнэ аргыг ойлгохын тулд эхлээд хамгийн бага квадратынхамгийн бага квадратын
зарчмыгзарчмыг авч зье.үавч зье.ү
• Хоёр хувьсагчийнХоёр хувьсагчийн PRF:PRF:
YYii == ββ11 + β+ β22XXii + u+ uii (2.4.2)(2.4.2)
• ЭнэЭнэ PRFPRF нь шууд ажиглагдахг йүнь шууд ажиглагдахг йү .. Бид нийгүүБид нийгүү SRFSRF-ээс нэлнэү-ээс нэлнэү ::
YYii == βˆβˆ11 + βˆ+ βˆ22XXii +uˆ+uˆii (2.6.2)(2.6.2)
== YˆYˆii +uˆ+uˆii (2.6.3)(2.6.3)
• ЭндЭнд YˆYˆii ньнь YYii –ийн нэлсэнү–ийн нэлсэнү ((н хц лт дундажө өн хц лт дундажө ө )) утгаутга..
• ГэвчГэвч SRFSRF хэрхэн тодорхойлогдох вэ?хэрхэн тодорхойлогдох вэ? ЭхлээдЭхлээд, (2.6.3), (2.6.3)-г хувиргавал-г хувиргавал
uˆuˆii = Y= Yii − Yˆ− Yˆii
== YYii −− βˆβˆ11 − βˆ− βˆ22XXii (3.1.1)(3.1.1)
• ОдооОдоо YY баба XX-ийн-ийн г гдс нө ө өг гдс нө ө ө nn хос ажиглалтыг ашигланхос ажиглалтыг ашиглан SRFSRF-г бодит-г бодит
-т аль болох д х хҮ ө ө-т аль болох д х хҮ ө ө аргаар тодорхойлж чаднааргаар тодорхойлж чадна.. Т гсг лд ньө өТ гсг лд ньө ө ,, бидбид
дараах шалгуурыг тавьж болнодараах шалгуурыг тавьж болно::
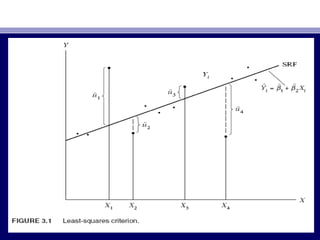
• лдэгдлийн нийлбэрҮлдэгдлийн нийлбэрҮ ˆˆuuii = (Y= (Yii − Yˆ− Yˆii)) аль болох бага байхаараль болох бага байхаар SRFSRF-г-г

3. • Гэвч энэ нь тийм ч сайн шалгуур биш юмГэвч энэ нь тийм ч сайн шалгуур биш юм.. Хэрэв бидХэрэв бид ˆˆuuii –г–г
минимумчилах шалгуур тавивал Зурагминимумчилах шалгуур тавивал Зураг 3.13.1-т харуулсан-т харуулсан
лдэгдэлүлдэгдэлү ˆˆuu22 баба ˆuˆu33 болон лдэгдэлүболон лдэгдэлү ˆuˆu11 баба ˆuˆu44 ньнь (ˆ(ˆuu11 + ˆu+ ˆu22 + ˆu+ ˆu33 + ˆu+ ˆu44))
нийлбэрт ижил жин авнанийлбэрт ижил жин авна.. р д нд ньҮ үр д нд ньҮ ү хэдийхэдий ˆˆuuii SRFSRF-ийн орчимд-ийн орчимд
рг н х рээтэй тархсан байсан чө ө үрг н х рээтэй тархсан байсан чө ө ү ˆˆuuii –ийн алгебр нийлбэр маш–ийн алгебр нийлбэр маш
багабага ((бараг тэгбараг тэг)) болно.болно.
• нийг харахын тулдҮүнийг харахын тулдҮү ,, ЗурагЗураг 3.13.1-т-т ˆuˆu11, ˆu, ˆu22, ˆu, ˆu33,, баба ˆuˆu44 нь харгалзаннь харгалзан
10, −2, +2,10, −2, +2, баба −10−10 утгууд авсан гэе.утгууд авсан гэе. ХэдийХэдий ˆˆuu11 баба ˆuˆu44 ньнь ˆˆuu22 баба ˆuˆu33 –аас–аас
ил рг н х рээнд тархсан байгаа ч эдгээр лдэгдлийнүү ө ө ү үил рг н х рээнд тархсан байгаа ч эдгээр лдэгдлийнүү ө ө ү ү
нийлбэр нь тэг гарч байна.нийлбэр нь тэг гарч байна.
• БидБид хамгийн бага квадратын шалгуурыгхамгийн бага квадратын шалгуурыг ашигласнаар энэашигласнаар энэ
асуудлаас зугтаж чадна.асуудлаас зугтаж чадна. SRFSRF нь дараах н хц лдө өнь дараах н хц лдө ө
ˆˆuu22
ii = (Y= (Yii − Yˆ− Yˆii))22
= (= (YYii −− βˆβˆ11 − βˆ− βˆ22XXii))22
(3.1.2)(3.1.2)
• аль болох хамгийн бага байхаль болох хамгийн бага байх,, эндэнд ˆuˆu22
ii нь лдэгдлийн квадратүнь лдэгдлийн квадратү ..

5. • ˆuˆuii –г квадрат зэрэг дэвш лснээр уг арга нь Зураг 3.1 дэхүү–г квадрат зэрэг дэвш лснээр уг арга нь Зураг 3.1 дэхүү
лдэгдэлүлдэгдэлү ˆˆuu11 баба ˆuˆu44-д-д ˆuˆu22 баба ˆuˆu33 –аас ил жин гн .үү ө ө–аас ил жин гн .үү ө ө
• Хамгийн бага квадрат аргын ндэслэл д нь энэ аргаарү үүХамгийн бага квадрат аргын ндэслэл д нь энэ аргаарү үү
олдсон нэлэлт дү үүолдсон нэлэлт дү үү зарим чухал статистик шинжзарим чухал статистик шинж
чанаруудтайчанаруудтай байдгийг бид удахг й знэ.ү үбайдгийг бид удахг й знэ.ү ү

6. • (3.1.2)(3.1.2)-оос харахад-оос харахад::
ˆˆuu22
ii == f (βˆf (βˆ11, βˆ, βˆ22)) (3.1.3)(3.1.3)
• лдэгдлийн квадрат нийлбэр ньҮлдэгдлийн квадрат нийлбэр ньҮ βˆβˆ11 баба βˆβˆ22 нэлэлт дийн функцү үүнэлэлт дийн функцү үү
байна. нийг харахын тулд Х снэгтҮү үбайна. нийг харахын тулд Х снэгтҮү ү 3.13.1 дэх хоёр туршилтыг авчдэх хоёр туршилтыг авч
зье.үзье.ү

7. • Хоёр туршилтынХоёр туршилтын βˆβˆ утгууд нь р байгаа тул бид нэлсэнөө үутгууд нь р байгаа тул бид нэлсэнөө ү
лдэгдлийн р утгууд олж авна.ү өөлдэгдлийн р утгууд олж авна.ү өө
• Одоо бидОдоо бид βˆβˆ -ийн ямар олонлогийг сонгох вэ-ийн ямар олонлогийг сонгох вэ?? Мэдээж эхнийМэдээж эхний
туршилтынтуршилтын βˆβˆ ньнь ““хамгийн сайнхамгийн сайн”” утгууд байнаутгууд байна.. БидБид
туршилтыг дуусгажтуршилтыг дуусгаж ˆˆuu22
ii –ийн боломжит хамгийн бага утга–ийн боломжит хамгийн бага утга
г хө өг хө ө βˆβˆ утгуудыг сонгох хэрэгтэй.утгуудыг сонгох хэрэгтэй.
• Гэвч цаг хугацаа болон х ч х д лм р хязгаартай тул бидү ө ө өГэвч цаг хугацаа болон х ч х д лм р хязгаартай тул бидү ө ө ө
туршилтын алдааны процессийн зарим асуудлыг авч зэхүтуршилтын алдааны процессийн зарим асуудлыг авч зэхү
хэрэгтэй.хэрэгтэй. Аз болоходАз болоход хамгийн бага квадрат арга ньхамгийн бага квадрат арга нь ˆˆuu22
ii-ийн-ийн
боломжит хамгийн бага утгыг гд гө өболомжит хамгийн бага утгыг гд гө ө ββ11 баба ββ22 –ийн–ийн ганцганц
нэлэлтээр хангадаг.үнэлэлтээр хангадаг.ү

8. ˆˆuu22
ii = (= (YYii −− βˆβˆ11 − βˆ− βˆ22XXii))22
(3.1.2)(3.1.2)

9. • Уламжлал ашигланУламжлал ашиглан ββ11 баба ββ22 –г нэлэх дараах тэгшитгэл дийг олжү үү–г нэлэх дараах тэгшитгэл дийг олжү үү
авнаавна::
YYii XXii == βˆβˆ11XXii ++ βˆβˆ22XX22
ii (3.1.4)(3.1.4)
YYii = n= nβˆβˆ11 + βˆ+ βˆ22XXii (3.1.5)(3.1.5)
• ЭндЭнд nn нь т врийн хэмжээүүнь т врийн хэмжээүү .. Уг систем тэгшитгэлийг нормальУг систем тэгшитгэлийг нормаль
тэгшитгэл д гэдэг.үүтэгшитгэл д гэдэг.үү Нормаль тэгшитгэл дийг нэгэн зэрэгүүНормаль тэгшитгэл дийг нэгэн зэрэгүү
шийдвэлшийдвэл,, дараах томъёо олдонодараах томъёо олдоно::

10. • ЭндЭнд X¯X¯ баба Y¯Y¯ ньнь XX баба YY т врийн дундаж б г дүү ө өөт врийн дундаж б г дүү ө өө xxii = (X= (Xii − X¯ )− X¯ ) баба
yyii = (Y= (Yii − Y¯)− Y¯) гэж тодорхойлж болно. Иймд бид цаашидгэж тодорхойлж болно. Иймд бид цаашид
жижиг сэг нь дунджаас хазайх хазайлтыг илэрхийлнэ гэжүжижиг сэг нь дунджаас хазайх хазайлтыг илэрхийлнэ гэжү
знэ.үзнэ.ү

11. • (3.1.7)(3.1.7) дахь с лийн алхам ньүүдахь с лийн алхам ньүү (3.1.4)(3.1.4)- с энгийн алгебр хувиргалтөө- с энгийн алгебр хувиргалтөө
хийх замаар шууд олдоно. Дашрамд дурдахад энгийн алгебрхийх замаар шууд олдоно. Дашрамд дурдахад энгийн алгебр
адилтгал ашиглах замаарадилтгал ашиглах замаар ββ22 –г нэлэхү–г нэлэхү томъёотомъёо (3.1.6)(3.1.6)-ийн-ийн
альтернатив хувилбар ньальтернатив хувилбар нь::
• мн олдсон нэлэлт дийгӨ ө ү үүмн олдсон нэлэлт дийгӨ ө ү үү хамгийн бага квадратын нэлэлтүхамгийн бага квадратын нэлэлтү
гэдэггэдэг..

12. • OLSOLS аргаар олдсон нэлэлт дийн дараах тоон шинж чанаруудыгү үүаргаар олдсон нэлэлт дийн дараах тоон шинж чанаруудыгү үү
тэмдэглэетэмдэглэе::
• I. OLSI. OLS нэлэлт д нь ажиглалтынү үүнэлэлт д нь ажиглалтынү үү ((жишээ ньжишээ нь,, т вэрүүт вэрүү )) нэгж дээрүүнэгж дээрүү
((жишээ ньжишээ нь,, XX баба Y)Y) илэрхийлэгддэгилэрхийлэгддэг.. ИймээсИймээс,, амархан тооцдогамархан тооцдог..
• II.II. Эдгээр нь цэгэн нэлэлт дү үүЭдгээр нь цэгэн нэлэлт дү үү ;; энэ нь г гдс н т врийн хувьдө ө ө үүэнэ нь г гдс н т врийн хувьдө ө ө үү
нэлэлт б р холбогдох эх олонлогийн параметрийн ганц утгаарү үнэлэлт б р холбогдох эх олонлогийн параметрийн ганц утгаарү ү
((интервал бишинтервал биш,, цэгэнцэгэн)) хангадаг.хангадаг.
• III. OLSIII. OLS нэлэлт нь т вэр г гдл с олдох тул т врийнү үү ө ө өө үүнэлэлт нь т вэр г гдл с олдох тул т врийнү үү ө ө өө үү
регрессийн шулуунрегрессийн шулуун ((ЗурагЗураг 3.1)3.1) хялбархан олдонохялбархан олдоно..
• Олдсон регрессийн шулуунОлдсон регрессийн шулуун дараах шинж чанаруудтай байнадараах шинж чанаруудтай байна::
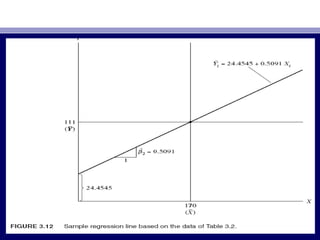
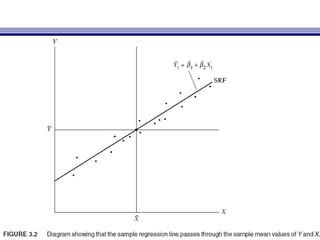
– 1.1. ба Х т врийн дунджийг дайран нг рн .Ү үү ө ө өба Х т врийн дунджийг дайран нг рн .Ү үү ө ө ө Энэ ньЭнэ нь (3.1.7)(3.1.7)-с-с
харахад ойлгомжтой бахарахад ойлгомжтой ба Y¯ = βˆY¯ = βˆ11 + βˆ+ βˆ22X¯X¯ ,, ЗурагЗураг 3.23.2-т диаграммаар-т диаграммаар
харуулсан болнохаруулсан болно..

14. – 2.2. нэлсэнҮнэлсэнҮ YˆYˆii -ийн дундаж утга нь-ийн дундаж утга нь бодитбодит YY-ийн-ийн дундаждундаж
утгатай тэнцүүутгатай тэнцүү::
YˆYˆii == βˆβˆ11 + βˆ+ βˆ22XXii
= (= (Y¯ − βˆY¯ − βˆ22X¯ ) + βˆX¯ ) + βˆ22XiXi
== Y¯ +Y¯ + βˆβˆ22((XXii − X¯)− X¯) (3.1.9)(3.1.9)
• С лийн тэгшитгэлийн хоёр талаас нийлбэр авч т врийн хэмжээүү үүС лийн тэгшитгэлийн хоёр талаас нийлбэр авч т врийн хэмжээүү үү
nn-д-д харьцуулвалхарьцуулвал
Y¯ˆ = Y¯Y¯ˆ = Y¯ (3.1.10)(3.1.10)
• эндэнд ((XXii − X¯ ) = 0− X¯ ) = 0 н хцлийг ашигласанөн хцлийг ашигласанө
– 3.3. лдэгдэл дундаж утгаҮлдэгдэл дундаж утгаҮ ¯¯ ˆˆuuii нь тэгнь тэг.. ХавсралтХавсралт 3A,3A, 3A.13A.1 хэсгээсхэсгээс,,
эхний тэгшитгэл ньэхний тэгшитгэл нь::
−−2(2(YYii −− βˆβˆ11 − βˆ− βˆ22XXii) = 0) = 0
• ЭндЭнд uˆuˆii = Y= Yii − βˆ− βˆ11 − βˆ− βˆ22XXii тул мн х тэгшитгэл ньө өтул мн х тэгшитгэл ньө ө
−−2 ˆ2 ˆuuii = 0,= 0, иймдиймд ¯ˆu = 0¯ˆu = 0

15. • мн х шинж чанарын р д нд т врийн регресс ньӨ ө ү ү үүмн х шинж чанарын р д нд т врийн регресс ньӨ ө ү ү үү
YYii == βˆβˆ11 + βˆ+ βˆ22XXii +uˆ+uˆii (2.6.2)(2.6.2)
• YY баба XX-г тэдгээрийн дунджаас хазайх хазайлтаар илэрхийлвэл-г тэдгээрийн дунджаас хазайх хазайлтаар илэрхийлвэл
альтернатив хэлбэрээр илэрхийлж болно.альтернатив хэлбэрээр илэрхийлж болно. нийг харахын тулдҮүнийг харахын тулдҮү
(2.6.2)(2.6.2)-ийн хоёр талаас нийлбэр авахад-ийн хоёр талаас нийлбэр авахад::
YYii = n= nβˆβˆ11 + βˆ+ βˆ22XXii +uˆ+uˆii
== nnβˆβˆ11 + βˆ+ βˆ22XXii эндэнд uˆuˆii = 0= 0 (3.1.11)(3.1.11)
• ТэгшитгэлТэгшитгэл (3.1.11)(3.1.11)-г-г nn-д харьцуулбал-д харьцуулбал
Y¯ = βˆY¯ = βˆ11 + βˆ+ βˆ22X¯X¯ (3.1.12)(3.1.12)
• (3.1.7)(3.1.7)-тай адил-тай адил.. ТэгшитгэлТэгшитгэл (2.6.2)(2.6.2)-оос-оос (3.1.12)(3.1.12)-г хасвал-г хасвал
YYii − Y¯ = βˆ− Y¯ = βˆ22(X(Xii − X¯ ) + uˆ− X¯ ) + uˆii
• ЭсвэлЭсвэл
yyii == βˆβˆ22xxii +uˆ+uˆii (3.1.13)(3.1.13)

16. • ТэгшитгэлТэгшитгэл (3.1.13)(3.1.13) ньнь хазайлтаар илэрхийлэгдсэн байнахазайлтаар илэрхийлэгдсэн байна..
Тогтмол параметрТогтмол параметр βˆβˆ11 энд алга байгааг тэмдэглэе. Гэвчэнд алга байгааг тэмдэглэе. Гэвч
тогтмол параметр нь ямагттогтмол параметр нь ямагт (3.1.7)(3.1.7)-р нэлэгдэнэү-р нэлэгдэнэү ,,
т врийн регрессийн шулуун ба Х т врийн дунджийгүү Ү үүт врийн регрессийн шулуун ба Х т врийн дунджийгүү Ү үү
дайрна.дайрна.
• Хазайлтаар илэрхийлсэн тэгшитгэлийн давуу тал ньХазайлтаар илэрхийлсэн тэгшитгэлийн давуу тал нь
тооцооллыг хялбар болгодогтооцооллыг хялбар болгодог.. Хазайлтаар илэрхийлсэнХазайлтаар илэрхийлсэн
хэлбэрээрхэлбэрээр SRFSRF нь дараах байдлаар бичигдэнэнь дараах байдлаар бичигдэнэ::
yˆyˆii == βˆβˆ22xxii (3.1.14)(3.1.14)
• Жинхэнэ хэмжилтийн нэгж ньЖинхэнэ хэмжилтийн нэгж нь (2.6.1)(2.6.1)-д харуулснаар-д харуулснаар
YˆYˆii = βˆ= βˆ11 + βˆ+ βˆ22XXii ..

17. – 4.4. лдэгдэлҮлдэгдэлҮ ˆˆuuii ньнь нэлсэнүнэлсэнү YYii-тэй корреляци хамааралг йү-тэй корреляци хамааралг йү ..
Дараах байдлаар баталнаДараах байдлаар батална:: хазайлтаар илэрхийлсэнхазайлтаар илэрхийлсэн
тэгшитгэлээртэгшитгэлээр::
– Энд дараах н хцлийг ашигласанөЭнд дараах н хцлийг ашигласанө
– 5.5. лдэгдэлҮлдэгдэлҮ ˆˆuuii ньнь XXii-тэй корреляци хамааралг йү-тэй корреляци хамааралг йү ;; ТэгшитгэлТэгшитгэл (2)(2)
ХавсралтХавсралт 3A, 3A.13A, 3A.1 хэсэг дэх н хцл р тайлбарлагданаө өөхэсэг дэх н хцл р тайлбарлагданаө өө ..

18. СОНГОДОГ ШУГАМАН РЕГРЕССИЙН ЗАГВАР:
ХАМГИЙН БАГА КВАДРАТЫН АРГЫН УРЬДЧИЛСАН Н ХЦЛ ДӨ ҮҮ
• Регрессийн шинжилгээнд бидний зорилго бол з вх нө өРегрессийн шинжилгээнд бидний зорилго бол з вх нө ө βˆβˆ11 баба
βˆβˆ22 –г олох бус харин жинхэнэ–г олох бус харин жинхэнэ ββ11 баба ββ22 –ийн талаар д гнэлтү–ийн талаар д гнэлтү
гаргах юмгаргах юм.. Жишээ ньЖишээ нь,, бидбид βˆβˆ11 баба βˆβˆ22 нь тэдгээрийн эхнь тэдгээрийн эх
олонлогийн утгатай хэр ойр,олонлогийн утгатай хэр ойр, YˆYˆii нь жинхэнэнь жинхэнэ E(Y | XE(Y | Xii)) утгатайутгатай
хэр ойр байгааг мэдэхийг х сдэг.үхэр ойр байгааг мэдэхийг х сдэг.ү
• PRFPRF-г харвал-г харвал:: YYii = β= β11 + β+ β22XXii + u+ uii .. ЭндЭнд YYii ньнь XXii баба uuii –аас хоёулангаас–аас хоёулангаас
нь хамаарч байна.нь хамаарч байна. XXii хувьсагчид болон алдааны утгынхувьсагчид болон алдааны утгын
талаарх урьдчилсан н хц л нь регрессийн нэлэлтийнө ө үталаарх урьдчилсан н хц л нь регрессийн нэлэлтийнө ө ү
х чин т г лд р тайлбарт маш чухал юм.ү ө ө өх чин т г лд р тайлбарт маш чухал юм.ү ө ө ө
• Гауссын стандарт буюуГауссын стандарт буюу сонгодог шугаман регрессийн загварсонгодог шугаман регрессийн загвар
((CLRMCLRM)) ньнь 1010 урьдчилсан н хц лтэйө өурьдчилсан н хц лтэйө ө ..

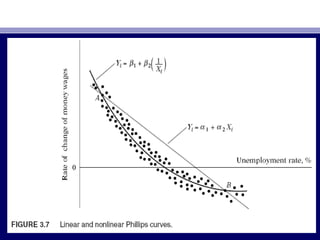
19. • Хамааран хувьсагчХамааран хувьсагч YY болон тайлбарлагч хувьсагчболон тайлбарлагч хувьсагч XX шугаман бишшугаман биш
байж болно гэдгийг санаарайбайж болно гэдгийг санаарай..

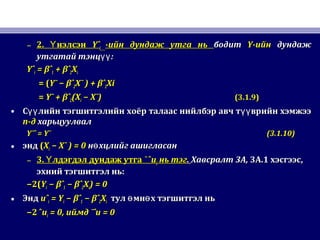
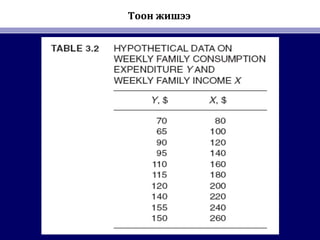
20. • Х снэгтүХ снэгтү 2.12.1-г хар-г хар.. Орлого Х-ийнОрлого Х-ийн $80$80 бэхлэгдсэн утганд бидбэхлэгдсэн утганд бид
санамсарг й нэг гэр б лийг сонгоход долоо хоногийнү үсанамсарг й нэг гэр б лийг сонгоход долоо хоногийнү ү
хэрэглээний зардалхэрэглээний зардал YY ньнь $60$60 байсанбайсан.. М нөМ нө X $80X $80 байхад рөөбайхад рөө
нэг гэр б лийг санамсарг й сонгоходү үнэг гэр б лийг санамсарг й сонгоходү ү YY утга ньутга нь $75$75 байвбайв..
Эдгээр т вэр тус б рийн хувьдүү үЭдгээр т вэр тус б рийн хувьдүү ү ((жишээ ньжишээ нь,, давталттайдавталттай
т вэрүүт вэрүү )) Х-ийн утгаХ-ийн утга $80$80 т вшинд бэхлэгдсэн байнаүт вшинд бэхлэгдсэн байнаү .. БидБид
х снэгт 2.1-т харуулсан б х Х утгын хувьд энэ процессыгү үх снэгт 2.1-т харуулсан б х Х утгын хувьд энэ процессыгү ү
давтаж чадна.давтаж чадна.
• Энэ нь бидний регрессийн шинжилгээ бол Х тайлбарлагчЭнэ нь бидний регрессийн шинжилгээ бол Х тайлбарлагч
хувьсагчдын г гдс н утгуудын н хц л дэхө ө ө ө өхувьсагчдын г гдс н утгуудын н хц л дэхө ө ө ө ө н хц лтө өн хц лтө ө
регрессийн шинжилгээрегрессийн шинжилгээ гэсэн г юм.үгэсэн г юм.ү

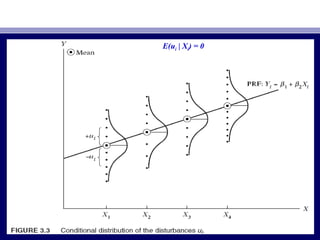
22. • ЗурагЗураг 3.33.3-д харуулснаар г гдс н Х-д харгалзах эх олонлогө ө ө Ү-д харуулснаар г гдс н Х-д харгалзах эх олонлогө ө ө Ү
б рийн хувьд зарим утга дунджаас дээг р, зарим ньү Ү үүб рийн хувьд зарим утга дунджаас дээг р, зарим ньү Ү үү
доогуур гэх мэтчилэн дундаж утгын ойролцоо тархсандоогуур гэх мэтчилэн дундаж утгын ойролцоо тархсан
байдагбайдаг.. г гдс н Х б рт харгалзах эдгээр хазайлтуудынӨ ө ө үг гдс н Х б рт харгалзах эдгээр хазайлтуудынӨ ө ө ү
дундаж утга нь тэг байнадундаж утга нь тэг байна..
• Урьдчилсан н хц лө өУрьдчилсан н хц лө ө E(uE(uii | X| Xii) = 0) = 0 ньнь E(YE(Yii | X| Xii) = β) = β11 + β+ β22XXii болохыгболохыг
баталдаг.баталдаг.

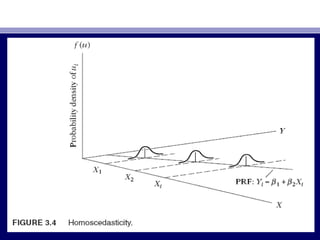
23. E(ui | Xi) = 0

24. • (3.2.2)(3.2.2) нь гомоскедастик буюунь гомоскедастик буюу ижилижил (homo)(homo) тархалттархалт (scedasticity)(scedasticity)
буюубуюу ижил дисперстэйижил дисперстэй байх урьдчилсан н хцлийг илэрхийлдэг.өбайх урьдчилсан н хцлийг илэрхийлдэг.ө
р рӨө өөр рӨө өө (3.2.2)(3.2.2) нь янз б рийн Х утгуудад харгалзах эх олонлог ньү Үнь янз б рийн Х утгуудад харгалзах эх олонлог ньү Ү
ижил дисперстэй байна гэсэн утгатай юм.ижил дисперстэй байна гэсэн утгатай юм.
• ЭнгийнээрЭнгийнээр,, регрессийн шулуунырегрессийн шулууны (( ба Х-ийн хоорондох дундажҮ ба Х-ийн хоорондох дундажҮ
хамаарлын шулуунхамаарлын шулуун)) орчим дахь хэлбэлзэл нь Х утгуудын хувьдорчим дахь хэлбэлзэл нь Х утгуудын хувьд
ижил байхижил байх;; Х-ийн рчл лт д сч, буурахг й байх.өө ө ө ө үХ-ийн рчл лт д сч, буурахг й байх.өө ө ө ө ү

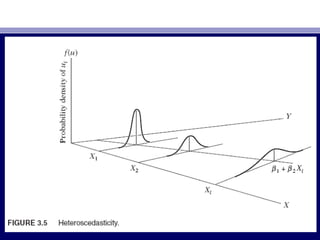
27. • ЗурагЗураг 3.53.5-д эх олонлогийн н хц лт дисперс нь Х-ээсҮ ө ө-д эх олонлогийн н хц лт дисперс нь Х-ээсҮ ө ө
хамаарч р р байна. Энэ н хцлийгөө өө өхамаарч р р байна. Энэ н хцлийгөө өө ө гетероскедастикгетероскедастик
буюу ижил бус тархалттай буюу дисперстэй гэдэг. нийгҮүбуюу ижил бус тархалттай буюу дисперстэй гэдэг. нийгҮү
(3.2.2)(3.2.2) н хц лд бичвэлө өн хц лд бичвэлө ө
• var (uvar (uii | X| Xii) =) = σσ22
ii (3.2.3)(3.2.3)
• ЗурагЗураг 3.53.5 var (var (u| Xu| X11) < var (u| X) < var (u| X22), . . . , < var (u| X), . . . , < var (u| Xii)) болохыгболохыг
харуулж байнахаруулж байна.. ИймээсИймээс X = XX = X11 н хц лд эх олонлогоос авсанө ө Үн хц лд эх олонлогоос авсанө ө Ү
ажиглалт ньажиглалт нь X = XX = X22, X = X, X = X33,, гэх мэт утганд харгалзах эхгэх мэт утганд харгалзах эх
олонлогоос олдсон утгуудаас илҮ үүолонлогоос олдсон утгуудаас илҮ үү PRFPRF-д ойрхон байх-д ойрхон байх
магадлалтай юм. Товчхондоо янз б рийн Х-тэй харгалзахүмагадлалтай юм. Товчхондоо янз б рийн Х-тэй харгалзахү
б х утгуудү Үб х утгуудү Ү ижил найдвартай бишижил найдвартай биш,, найдвартай байдал ньнайдвартай байдал нь
утгууд дунджийнхаа орчимҮ утгууд дунджийнхаа орчимҮ ((PRFPRF дээрх цэг дүүдээрх цэг дүү )) хэр ойрхэр ойр
эсвэл хол тархсан байгаагаар хэмжигдэнэ.эсвэл хол тархсан байгаагаар хэмжигдэнэ.

28. • З рө үүЗ рө үү uuii баба uujj нь корреляци хамааралг йүнь корреляци хамааралг йү ,, жишээ ньжишээ нь,, сериалсериал
корреляци байхг йүкорреляци байхг йү .. Энэ нь г гдс нө ө өЭнэ нь г гдс нө ө ө XXii хувьдхувьд аливаа хоёр утгынҮаливаа хоёр утгынҮ
дунджаасаа хазайх хазайлт нь ямар нэг хэв загварг й байнаүдунджаасаа хазайх хазайлт нь ямар нэг хэв загварг й байнаү ..
ЗурагЗураг 3.6a3.6a-д-д uu нь эерэг корреляци хамааралтай байна. Зурагнь эерэг корреляци хамааралтай байна. Зураг 3.6b3.6b-д-д
uu нь с р г корреляци хамааралтай байнаө өнь с р г корреляци хамааралтай байнаө ө .. Хэрэв з р н дө үү үүХэрэв з р н дө үү үү
системт хэв загвартай байвалсистемт хэв загвартай байвал ((зурагзураг 3.63.6aa болонболон b)b) авто буюуавто буюу
сериал корреляцитай байнасериал корреляцитай байна.. ЗурагЗураг 3.63.6cc-д-д uu нь системтнь системт
хамааралг й буюу тэг корреляцитай байгааг харуулж байна.үхамааралг й буюу тэг корреляцитай байгааг харуулж байна.ү

30. • БиднийБидний PRF (PRF (YYtt = β= β11 + β+ β22XXtt + u+ utt))-ийн хувьд-ийн хувьд uutt баба uut−1t−1 нь эерэгнь эерэг
корреляци хамааралтай гэе. Тэгвэлкорреляци хамааралтай гэе. Тэгвэл YYtt нь з вх нө өнь з вх нө ө XXtt-ээс-ээс
хамаарахг й м н басү өхамаарахг й м н басү ө uut−1t−1-ээс хамаарна.-ээс хамаарна. uut−1t−1 ньнь uutt-ийн зарим-ийн зарим
хэсгийг тодорхойлдог.хэсгийг тодорхойлдог.

31. • З рө үүЗ рө үү uu болонболон тайлбарлагч хувьсагчтайлбарлагч хувьсагч XX ньнь корреляци хамааралг йүкорреляци хамааралг йү ..
PRFPRF ньнь XX баба uu (which may represent(which may represent the influence of all the omittedthe influence of all the omitted
variables)variables) ньнь YY-т тус тусдаа-т тус тусдаа ((нэмэлтнэмэлт)) н л лн гэж знэ.ө өө ө үн л лн гэж знэ.ө өө ө ү Гэвч хэрэвГэвч хэрэв
XX баба uu ньнь корреляци хамааралтайкорреляци хамааралтай бол тэдгээрийн -т з лэх тусҮ ү үүбол тэдгээрийн -т з лэх тусҮ ү үү
тусын н л г нэлэх боломжг й юм. Иймд хэрэвө өө ү үтусын н л г нэлэх боломжг й юм. Иймд хэрэвө өө ү ү XX баба uu нь эерэгнь эерэг
хамааралтай эсвэл с р г хамааралтай болө өхамааралтай эсвэл с р г хамааралтай болө ө XX баба uu-ийн -тҮ-ийн -тҮ
з лэх н л гү үү ө өөз лэх н л гү үү ө өө тусгаарлахад хэц .үүтусгаарлахад хэц .үү

32. • Х снэгтүХ снэгтү 3.13.1-ийн жишээнд бидэнд ба Х-ийн з вх н эхний ганцҮ ө ө-ийн жишээнд бидэнд ба Х-ийн з вх н эхний ганцҮ ө ө
хос ажиглалт байгаа гэж т с льеө өөхос ажиглалт байгаа гэж т с льеө өө (4(4 баба 1).1). Энэ ганц ажиглалтаасЭнэ ганц ажиглалтаас
л мэдэгдэхүл мэдэгдэхү ββ11 баба ββ22 –г нэлэх боломжг йү ү–г нэлэх боломжг йү ү .. Бидэнд хамгийн багадааБидэнд хамгийн багадаа
хоёр хос ажиглалт хэрэгтэй.хоёр хос ажиглалт хэрэгтэй.

33. • Энэ урьдач н хц л нь харагдаж байгаа шигээ энгийн биш юмө өЭнэ урьдач н хц л нь харагдаж байгаа шигээ энгийн биш юмө ө ..
ТэгшитгэлТэгшитгэл (3.1.6)(3.1.6)-г хар-г хар.. Хэрэв б хүХэрэв б хү XX утгууд ижил болутгууд ижил бол XXii = X¯= X¯ болохболох
ба энэ ед тэгшитгэлийн хуваарь тэг болох баүба энэ ед тэгшитгэлийн хуваарь тэг болох баү β2β2 баба β1β1-г нэлэхү-г нэлэхү
боломжг й болноүболомжг й болноү .. 2-р б лгийн рхийн хэрэглээний зардлынү ө2-р б лгийн рхийн хэрэглээний зардлынү ө
жишээг харвал хэрэв рхийн орлого маш бага хэлбэлзэлтэй болөжишээг харвал хэрэв рхийн орлого маш бага хэлбэлзэлтэй болө
бид хэрэглээний зардлын хэлзэлзлийн ихэнх хэсгийг тайлбарлахбид хэрэглээний зардлын хэлзэлзлийн ихэнх хэсгийг тайлбарлах
боломжг й болно.үболомжг й болно.ү

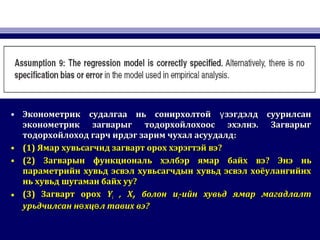
34. • Эконометрик судалгаа нь сонирхолтой зэгдэлд суурилсанүЭконометрик судалгаа нь сонирхолтой зэгдэлд суурилсанү
эконометрик загварыг тодорхойлохоос эхэлнэ. Загварыгэконометрик загварыг тодорхойлохоос эхэлнэ. Загварыг
тодорхойлоход гарч ирдэг зарим чухал асуудалдтодорхойлоход гарч ирдэг зарим чухал асуудалд::
• (1)(1) Ямар хувьсагчид загварт орох хэрэгтэй вэЯмар хувьсагчид загварт орох хэрэгтэй вэ??
• (2)(2) Загварын функциональ хэлбэр ямар байх вэЗагварын функциональ хэлбэр ямар байх вэ?? Энэ ньЭнэ нь
параметрийн хувьд эсвэл хувьсагчдын хувьд эсвэл хоёулангийнхпараметрийн хувьд эсвэл хувьсагчдын хувьд эсвэл хоёулангийнх
нь хувьд шугаман байх уунь хувьд шугаман байх уу??
• (3)(3) Загварт орохЗагварт орох YYii , X, Xii,, болонболон uuii-ийн хувьд ямар магадлалт-ийн хувьд ямар магадлалт
урьдчилсан н хц л тавих вэө өурьдчилсан н хц л тавих вэө ө ??

35. • Нэрлэсэн цалингийн рчл лтийн хувь болон ажилг йдлийнөө ө үНэрлэсэн цалингийн рчл лтийн хувь болон ажилг йдлийнөө ө ү
т вшингийн хоорондох хамаарлыг илэрхийлэх дараах хоёрүт вшингийн хоорондох хамаарлыг илэрхийлэх дараах хоёрү
загварыг авч зье:үзагварыг авч зье:ү
• YYii == αα11 + α+ α22XXii + u+ uii (3.2.7)(3.2.7)
• YYii == ββ11 + β+ β22 ((11/X/Xii ) + u) + uii (3.2.8)(3.2.8)
• ЭндЭнд YYii == нэрлэсэн цалингийн рчл лтийн хувьөө өнэрлэсэн цалингийн рчл лтийн хувьөө ө ,, баба XXii ==
ажилг йдлийн т вшинү үажилг йдлийн т вшинү ү .. Регрессийн загварРегрессийн загвар (3.2.7)(3.2.7) нь параметрнь параметр
болон хувьсагчдын хувьд шугаман болболон хувьсагчдын хувьд шугаман бол (3.2.8)(3.2.8) нь параметрийннь параметрийн
хувьд шугаман, хувьсагчхувьд шугаман, хувьсагч XX-ийн хувьд шугаман бус байна-ийн хувьд шугаман бус байна.. ОдооОдоо
зурагзураг 3.73.7-г авч зьеү-г авч зьеү ..
• Хэрэв загварХэрэв загвар (3.2.8)(3.2.8) ньнь ““з вөз вө ”” загвар бол зураг 3.7 дахь скаттерзагвар бол зураг 3.7 дахь скаттер
цэг дэд загварүүцэг дэд загварүү (3.2.7)(3.2.7)-г нийц лэх нь буруу нэлэлтэд х ргэнэ.үү ү ү-г нийц лэх нь буруу нэлэлтэд х ргэнэ.үү ү ү
• Харамсалтай нь практикт тусгай судалгаанд суурилсан онолынХарамсалтай нь практикт тусгай судалгаанд суурилсан онолын
хувьд з в хувьсагчид загварт орсон эсэх, загварын з вө өхувьд з в хувьсагчид загварт орсон эсэх, загварын з вө ө
функциональ хэлбэр м н эсэх, загварт орж буй хувьсагчдынөфункциональ хэлбэр м н эсэх, загварт орж буй хувьсагчдынө
талаар з в магадлалт таамаглал дэвш лсэн эсэх б х асуултадө үү үталаар з в магадлалт таамаглал дэвш лсэн эсэх б х асуултадө үү ү
хангалттай сайн хариулж чадахг й байж болно.үхангалттай сайн хариулж чадахг й байж болно.ү

37. • Бид уг урьдчилсан н хцлийг б лэгө үБид уг урьдчилсан н хцлийг б лэгө ү 77-д олон хэмжээст регрессийн-д олон хэмжээст регрессийн
загварын сэдвээр авч знэ.үзагварын сэдвээр авч знэ.ү

38. НАРИЙВЧЛАЛ БУЮУ ХАМГИЙН БАГА КВАДРАТ
НЭЛЭЛТИЙН СТАНДАРТ АЛДААҮ
• Хамгийн бага квадрат нэлэлт ньүХамгийн бага квадрат нэлэлт ньү т вэр г гдлийн функц юмүү ө өт вэр г гдлийн функц юмүү ө ө ..
Гэвч т врээс т вэрт г гд л рчл гдв л нэлэлт басүү үү ө ө ө өө ө ө үГэвч т врээс т вэрт г гд л рчл гдв л нэлэлт басүү үү ө ө ө өө ө ө ү
рчл гд н . Иймээсөө ө ө өрчл гд н . Иймээсөө ө ө ө βˆβˆ11 баба βˆβˆ22 нэлэлт дийн нарийвчлал буюуү үүнэлэлт дийн нарийвчлал буюуү үү
““найдвартай байдалнайдвартай байдал”” нь чухал юм. Статистикт нэлэлтийнүнь чухал юм. Статистикт нэлэлтийнү
нарийвчлалнарийвчлал стандарт алдаагаарстандарт алдаагаар (se)(se) хэмжигддэг:хэмжигддэг:

39. • σσ22
нь урьдчилсан н хц л 4-ийн дагууө өнь урьдчилсан н хц л 4-ийн дагууө ө uuii –ийн тогтмол дисперс юм.–ийн тогтмол дисперс юм.
• σσ22
дараах томъёогоор тооцогдонодараах томъёогоор тооцогдоно::
• эндэнд ˆˆσσ22
нь жинхэнэ буюунь жинхэнэ буюу л мэдэгдэхүл мэдэгдэхү σσ22
-ийн-ийн OLSOLS нэлэлт ба эндүнэлэлт ба эндү n−2n−2
нь ч л ний зэрэгө өөнь ч л ний зэрэгө өө (df),(df), нь лдэгдлийн квадрат нийлбэрүнь лдэгдлийн квадрат нийлбэрү ((RSSRSS).).
ИймдИймд мэдэгдэж байвалмэдэгдэж байвал ˆˆσσ22
хялбар тооцогдонохялбар тооцогдоно..
• ТэгшитгэлТэгшитгэл (3.3.6)(3.3.6)-г тэгшитгэл-г тэгшитгэл (3.1.2)(3.1.2)-той харьцуулахад ажиглалт-той харьцуулахад ажиглалт
тус б рийн хувьдүтус б рийн хувьдү ˆˆuuii –г тооцох шаардлагаг й тул ашиглахадү–г тооцох шаардлагаг й тул ашиглахадү
хялбар юм.хялбар юм.

40. • ЭндЭнд
• -г тооцох альтернатив илэрхийлэл нь-г тооцох альтернатив илэрхийлэл нь
• Дашрамд хэлэхэдДашрамд хэлэхэд ˆˆσσ22
–ийн эерэг квадрат язгуурыг–ийн эерэг квадрат язгуурыг
• нэлэлтийн стандарт алдааүнэлэлтийн стандарт алдааү буюу регрессийн стандарт алдаабуюу регрессийн стандарт алдаа (se)(se)
гэдэггэдэг.. Энэ нь энгийнээр нэлэгдсэн регрессийн шулууны хувьдү ҮЭнэ нь энгийнээр нэлэгдсэн регрессийн шулууны хувьдү Ү
утгуудын стандарт хазайлт б г д регрессийн шулууны “нийцтэйө өөутгуудын стандарт хазайлт б г д регрессийн шулууны “нийцтэйө өө
байдлын” р д нгийн хэмжигдэх н болж ашиглагддаг.ү ү үүбайдлын” р д нгийн хэмжигдэх н болж ашиглагддаг.ү ү үү

41. • βˆβˆ11 баба βˆβˆ22 –ийн дисперсийн дараах м н чанаруудыг тэмдэглэеө–ийн дисперсийн дараах м н чанаруудыг тэмдэглэеө
((м н т нчлэн стандарт алдаагө үүм н т нчлэн стандарт алдаагө үү ))..
• 1.1. βˆβˆ22 –ийн дисперс нь–ийн дисперс нь σσ22
-тай шууд пропорциональ,-тай шууд пропорциональ, xx22
ii-тай урвуу-тай урвуу
пропорциональ хамааралтай. Энд г гдс нө ө өпропорциональ хамааралтай. Энд г гдс нө ө ө σσ22
-ийн хувьд-ийн хувьд XX
утгуудын хэлбэлзэл их байх ньутгуудын хэлбэлзэл их байх нь βˆβˆ22-ийн дисперс бага байх, улмаар-ийн дисперс бага байх, улмаар
ββ22 ил нарийвчлалтай нэлэгдэнэ гэсэн гүү ү үил нарийвчлалтай нэлэгдэнэ гэсэн гүү ү ү ..
• 2.2. βˆβˆ11 –ийн дисперс нь–ийн дисперс нь σσ22
болонболон XX22
ii –тай шууд пропорциональ,–тай шууд пропорциональ, xx22
ii
болон т врийн хэмжээүүболон т врийн хэмжээүү nn--тай урвуу пропорциональтай урвуу пропорциональ
хамааралтай.хамааралтай.

42. • 3.3. βˆβˆ11 баба βˆβˆ22 нэлэлт д нь з вх н т врээс т вэртү үү ө ө үү үүнэлэлт д нь з вх н т врээс т вэртү үү ө ө үү үү
рчл гдд гг йөө ө ө үрчл гдд гг йөө ө ө ү ба г гдс н т вэртө ө ө үүба г гдс н т вэртө ө ө үү бие биенээсээ хамааралтайбие биенээсээ хамааралтай
байж болохбайж болох ба уг хамаарлыг тэдгээрийн хоорондын ковариациарба уг хамаарлыг тэдгээрийн хоорондын ковариациар
хэмждэг.хэмждэг.
• var (var (βˆβˆ22)) ньнь ргэлж эерэгүргэлж эерэгү байх тулбайх тул βˆβˆ11 баба βˆβˆ22 –ийн хоорондох–ийн хоорондох
ковариацийн чанар ньковариацийн чанар нь X¯X¯ -ийн тэмдгээс хамаарна-ийн тэмдгээс хамаарна.. ХэрэвХэрэв X¯X¯ нь эерэгнь эерэг
бол ковариаци с р г болохыг томъёо харуулж байна. Иймд хэрэвө өбол ковариаци с р г болохыг томъёо харуулж байна. Иймд хэрэвө ө
нцгийн коэффициентөнцгийн коэффициентө ββ22 нь ил нэлэгдвэлүү үнь ил нэлэгдвэлүү ү ((жишээ ньжишээ нь,, налалтналалт
нь огцом байнань огцом байна)) болбол тогтмол коэффициенттогтмол коэффициент ββ11 дутуу нэлэгдэнэүдутуу нэлэгдэнэү
((жишээ ньжишээ нь,, тогтмол коэффициент маш бага байнатогтмол коэффициент маш бага байна).).

43. ХАМГИЙН БАГА КВАДРАТ НЭЛЭЛТИЙН ШИНЖ ЧАНАР:Ү
ГАУСС-МАРКОВЫН ТЕОРЕМ
• Уг теоремийг ойлгохын тулд бид нэлэлтийн хамгийн сайнүУг теоремийг ойлгохын тулд бид нэлэлтийн хамгийн сайнү
шугаман хазайлтг й шинж чанарыг авч зэх хэрэгтэйү үшугаман хазайлтг й шинж чанарыг авч зэх хэрэгтэйү ү . OLS. OLS
нэлэлтүнэлэлтү βˆβˆ22 нь дараах н хцлийг хангасан едө үнь дараах н хцлийг хангасан едө ү ββ22 –ийн хамгийн сайн–ийн хамгийн сайн
шугаман хазайлтг й нэлэлтү үшугаман хазайлтг й нэлэлтү ү (BLUE)(BLUE) болноболно::
• 1.1. Регрессийн загвар дахь хамааран хувьсагч буюу санамсарг йүРегрессийн загвар дахь хамааран хувьсагч буюу санамсарг йү
хувьсагч -ийн хувьдҮхувьсагч -ийн хувьдҮ шугаман функцшугаман функц байна.байна.
• 2.2. Дундаж буюу х лээгдэж буй утгаүДундаж буюу х лээгдэж буй утгаү E(βˆE(βˆ22)) нь жинхэнэ утгань жинхэнэ утга ββ22-тай-тай
тэнц буюуүүтэнц буюуүү хазайлтг й байна.үхазайлтг й байна.ү
• 3.3. Б х шугаман хазайлтг й нэлэлт дийн ангидү ү ү үүБ х шугаман хазайлтг й нэлэлт дийн ангидү ү ү үү хамгийн багахамгийн бага
дисперстэй байхдисперстэй байх ба хамгийн бага дисперстэй хазайлтг й нэлэлтү үба хамгийн бага дисперстэй хазайлтг й нэлэлтү ү
нь р ашигтай нэлэлт болноү үнь р ашигтай нэлэлт болноү ү ..

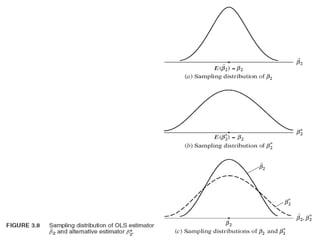
44. • Энэ б гдийг зурагүЭнэ б гдийг зурагү 3.83.8-ийн тусламжтайгаар тайлбарлаж болно-ийн тусламжтайгаар тайлбарлаж болно..
ЗурагЗураг 3.8(3.8(a)a)-д давталттай т врийн туршилтадүү-д давталттай т врийн туршилтадүү βˆβˆ22-ийн авах-ийн авах
утгуудын тархалт болохутгуудын тархалт болох OLSOLS нэлэлтүнэлэлтү βˆβˆ22 –ийн т вэр тархалтыгүү–ийн т вэр тархалтыгүү
харуулсанхаруулсан.. Тохиромжтой байхын тулд бидТохиромжтой байхын тулд бид βˆβˆ22 тэгш хэмтэйтэгш хэмтэй
тархсан гэж зсэнүтархсан гэж зсэнү .. Зурагт харуулснаарЗурагт харуулснаар βˆβˆ22 утгуудын дундажутгуудын дундаж E(βˆE(βˆ22))
нь жинхэнэнь жинхэнэ ββ22-той тэнц байна. Энэ н хц лдүү ө ө-той тэнц байна. Энэ н хц лдүү ө ө βˆβˆ22 ньнь ββ22-ийн-ийн
хазайлтг й нэлэлт болно. Зурагү үхазайлтг й нэлэлт болно. Зурагү ү 3.8(b)3.8(b)-д-д р аргаөөр аргаөө ((жишээ нь,жишээ нь,
OLSOLS-с рөө-с рөө )) ашиглан олсонашиглан олсон ββ22-ийн альтернатив нэлэлт болохү-ийн альтернатив нэлэлт болохү β∗β∗22 ––
ийн т вэр тархалтыг харуулсан.үүийн т вэр тархалтыг харуулсан.үү

46. • Тохиромжтой байхын тулдТохиромжтой байхын тулд βˆβˆ22 –ийн адил–ийн адил β*β*22 нь хазайлтг й гэжүнь хазайлтг й гэжү
звэл дундаж буюу х лээгдэж буй утга ньү үзвэл дундаж буюу х лээгдэж буй утга ньү ү ββ22-той тэнц байна.үү-той тэнц байна.үү βˆβˆ22
баба β*β*22 хоёул шугаман нэлэлт д гэвэл тэдү үүхоёул шугаман нэлэлт д гэвэл тэдү үү YY-ийн шугаман функц-ийн шугаман функц
байнабайна. βˆ. βˆ22 баба β*β*22-ын аль нэлэлтийг сонгох вэү-ын аль нэлэлтийг сонгох вэү ?? Энэ асуултадЭнэ асуултад
хариулахын тулд хоёр зургийг зурагхариулахын тулд хоёр зургийг зураг 3.8(3.8(c)c)-д давхарлан тавьж-д давхарлан тавьж
з льеү үүз льеү үү .. Энд хэдийгээрЭнд хэдийгээр βˆβˆ22 баба β*β*22 нь хазайлтг й боловчүнь хазайлтг й боловчү β*β*22-ийн-ийн
тархалт ньтархалт нь βˆβˆ22 –ийн тархалтаас ил дундаж утгынхаа орчимүү–ийн тархалтаас ил дундаж утгынхаа орчимүү
сарнимал буюу рг н тархсан байнаө өсарнимал буюу рг н тархсан байнаө ө .. р р хэлбэлӨө өөр р хэлбэлӨө өө , β*, β*22-ийн-ийн
дисперс ньдисперс нь βˆβˆ22-ийн дисперсээс их байна.-ийн дисперсээс их байна.
• Одоо г гдс н хоёр нэлэлт хоёулаа шугаман ба хазайлтг й тулө ө ө ү үОдоо г гдс н хоёр нэлэлт хоёулаа шугаман ба хазайлтг й тулө ө ө ү ү
альтернатив нэлэлтээс илү үүальтернатив нэлэлтээс илү үү ββ22 –д д х х магадлалтай багаө ө–д д х х магадлалтай багаө ө
дисперстэй нэлэлтийг нь сонгоно.үдисперстэй нэлэлтийг нь сонгоно.ү ТовчхондооТовчхондоо BLUEBLUE нэлэлтийгүнэлэлтийгү
сонгоно.сонгоно.

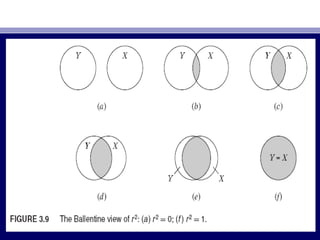
47. ДЕТЕРМИНАЦИЙН КОЭФФИЦИЕНТ r2
:
“НИЙЦТЭЙ” БАЙДЛЫН ХЭМЖИГДЭХ НҮҮ
• Т врийн регрессийн шулуун г гд лд хэр “сайн” нийцтэйүү ө ө өТ врийн регрессийн шулуун г гд лд хэр “сайн” нийцтэйүү ө ө ө
байгааг илэрхийлдэгбайгааг илэрхийлдэг нийцтэй байдлын хэмжигдэх нийгүүнийцтэй байдлын хэмжигдэх нийгүү авчавч
зье. Детерминацийн коэффициентүзье. Детерминацийн коэффициентү rr22
((хос регрессийн тохиолдолдхос регрессийн тохиолдолд))
эсвэлэсвэл RR22
((олон х чин з йлийн регрессү үолон х чин з йлийн регрессү ү )) ньнь т врийн регрессийнүүт врийн регрессийнүү
шулуун г гд лд хэр нийцтэй байгааг илэрхийлдэг р д нгийнө ө ө ү үшулуун г гд лд хэр нийцтэй байгааг илэрхийлдэг р д нгийнө ө ө ү ү
хэмжигдэх н.үүхэмжигдэх н.үү
• rr22
-ийн хьюристик тайлбарыг зураг 3.9 дэх Венний диаграммаар-ийн хьюристик тайлбарыг зураг 3.9 дэх Венний диаграммаар
авч зье.үавч зье.ү
• Энэ зурагтЭнэ зурагт YY дугуй нь хамааран хувьсагч -ийн хэлбэлзлийгҮдугуй нь хамааран хувьсагч -ийн хэлбэлзлийгҮ
илэрхийлэх болилэрхийлэх бол XX дугуй нь тайлбарлагч хувьсагч Х-ийн хэлбэлзлийгдугуй нь тайлбарлагч хувьсагч Х-ийн хэлбэлзлийг
илэрхийлнэ. Хоёр дугуйн давхцал нь Х-ийн хэлзэлзлээрилэрхийлнэ. Хоёр дугуйн давхцал нь Х-ийн хэлзэлзлээр
тайлбарлагдаж буй -ийн хэлбэлзлийг илэрхийлнэ.Үтайлбарлагдаж буй -ийн хэлбэлзлийг илэрхийлнэ.Ү

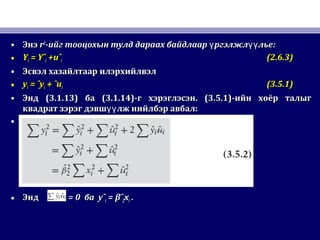
49. • ЭнэЭнэ rr22
-ийг тооцохын тулд дараах байдлаар ргэлжл льеү үү-ийг тооцохын тулд дараах байдлаар ргэлжл льеү үү ::
• YYii = Yˆ= Yˆii +uˆ+uˆii (2.6.3)(2.6.3)
• Эсвэл хазайлтаар илэрхийлвэлЭсвэл хазайлтаар илэрхийлвэл
• yyii = ˆy= ˆyii + ˆu+ ˆuii (3.5.1)(3.5.1)
• ЭндЭнд (3.1.13)(3.1.13) баба (3.1.14)(3.1.14)-г хэрэглэсэн-г хэрэглэсэн. (3.5.1). (3.5.1)-ийн хоёр талыг-ийн хоёр талыг
квадрат зэрэг дэвш лж нийлбэр авбал:үүквадрат зэрэг дэвш лж нийлбэр авбал:үү
•
• ЭндЭнд = 0= 0 баба yˆyˆii = βˆ= βˆ22xxii ..

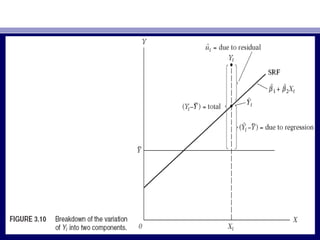
50. • (3.5.2)(3.5.2)-ийн квадрат нийлбэр д ньүү-ийн квадрат нийлбэр д ньүү дараах байдлаардараах байдлаар
тодорхойлогдонотодорхойлогдоно:: == бодит -ийн дунджаасааҮбодит -ийн дунджаасааҮ
хазайх нийт хазайлтхазайх нийт хазайлт,, Б тэн квадрат нийлбэр гэж нэрлэдэгүБ тэн квадрат нийлбэр гэж нэрлэдэгү ((TSSTSS).).
• == нэлэгдсэн утгуудынү Үнэлэгдсэн утгуудынү Ү
дунджаасаа хазайх хазайлтдунджаасаа хазайх хазайлт(¯ˆ(¯ˆY = Y¯),Y = Y¯), регрессээр тайлбарлагдажрегрессээр тайлбарлагдаж
буй квадрат нийлбэрбуй квадрат нийлбэр,, буюу энгийнээрбуюу энгийнээр регрессийн квадратрегрессийн квадрат
нийлбэрнийлбэр (ESS).(ESS). == утгуудын регрессийн шулуунаарҮ утгуудын регрессийн шулуунаарҮ
тайлбарлагдахг й хэлбэлзэл буюу энгийнээрүтайлбарлагдахг й хэлбэлзэл буюу энгийнээрү лдэгдлийн квадратүлдэгдлийн квадратү
нийлбэрнийлбэр (RSS).(RSS). ИймдИймд, (3.5.2), (3.5.2) ньнь
• TSS = ESS + RSSTSS = ESS + RSS (3.5.3)(3.5.3)
• Ажиглалтын утгуудын дунджаасаа хазайх нийт хэлбэлзэл ньҮАжиглалтын утгуудын дунджаасаа хазайх нийт хэлбэлзэл ньҮ
хоёр хэсэгт хуваагданахоёр хэсэгт хуваагдана,, нэг нь регрессийн шулуунд хамаарах болнэг нь регрессийн шулуунд хамаарах бол
н г нь б х бодит ажиглалтууд шулуун дээр байршихг й тулө өө ү Ү үн г нь б х бодит ажиглалтууд шулуун дээр байршихг й тулө өө ү Ү ү
санамсарг й х чин з йлтэй холбоотойү ү үсанамсарг й х чин з йлтэй холбоотойү ү ү .. Геометрийн хувьдГеометрийн хувьд,, ЗурагЗураг
3.103.10-г авч зье.ү-г авч зье.ү

53. • rr22
буюу т врийн детерминацийн коэффициент нь регрессийнүүбуюу т врийн детерминацийн коэффициент нь регрессийнүү
шулууны нийцтэй байдлыг хэмжихэд хамгийн нийтлэгшулууны нийцтэй байдлыг хэмжихэд хамгийн нийтлэг
ашиглагддаг хэмжигдэх н юмүүашиглагддаг хэмжигдэх н юмүү .. rr22
ньнь регрессийн загварааррегрессийн загвараар
тайлбарлагдаж байгаа -ийн нийт хэлбэлзлийн хувийг хэмждэг.Үтайлбарлагдаж байгаа -ийн нийт хэлбэлзлийн хувийг хэмждэг.Ү
• rr22
–ийн хёор шинж чанарыг тэмдэглэвэл–ийн хёор шинж чанарыг тэмдэглэвэл::
• 1.1. С р г утга авахг йө ө үС р г утга авахг йө ө ү ..
• 22. 0 ≤. 0 ≤ rr22
≤ 1≤ 1 завсарт утгаа авназавсарт утгаа авна.. rr22
ньнь 11 утга авбал т гс нийцтэйөутга авбал т гс нийцтэйө
байдлыг илэрхийлнэбайдлыг илэрхийлнэ, i, i б рийн хувьдүб рийн хувьдү YˆYˆii = Y= Yii .. Н г талаасө өөН г талаасө өө , r, r22
нь тэгнь тэг
бол хамааран болон тайлбарлагч хувьсагч хоорондообол хамааран болон тайлбарлагч хувьсагч хоорондоо
хамааралг йг илэрхийлнэүхамааралг йг илэрхийлнэү ((жишээ ньжишээ нь,, βˆβˆ22 = 0).= 0). Энэ тохиолдолдЭнэ тохиолдолд
(3.1.9)(3.1.9) ньнь YˆYˆii = βˆ= βˆ11 = Y¯= Y¯ болохыг харуулдаг буюу ямар нэг утгынҮболохыг харуулдаг буюу ямар нэг утгынҮ
хамгийн сайн нэлэлт нь т ний дундаж утга байнаү үүхамгийн сайн нэлэлт нь т ний дундаж утга байнаү үү .. ЭнэЭнэ
н хц лд регрессийн шулуун Х тэнхлэгийн хувьд хэвтээ болно.ө өн хц лд регрессийн шулуун Х тэнхлэгийн хувьд хэвтээ болно.ө ө
• ХэдийгээрХэдийгээр rr22
(3.5.5)(3.5.5)-д г гдс н тодорхойлолтоос шууд тооцогдожө ө ө-д г гдс н тодорхойлолтоос шууд тооцогдожө ө ө
болох ч дараах томъёогоор ил хурдан олдоноүүболох ч дараах томъёогоор ил хурдан олдоноүү ::

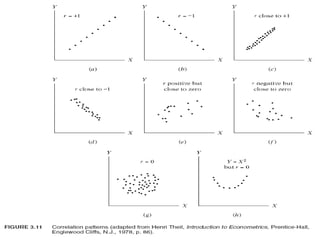
57. • rr –ийн зарим шинж чанарууд нь–ийн зарим шинж чанарууд нь ((ЗурагЗураг 3.113.11-г хар-г хар):):
• 1.1. Эерэг ба с р г утга авч болноө өЭерэг ба с р г утга авч болноө ө ,,
• 2.2. −1−1 баба +1+1 хооронд утгаа авнахооронд утгаа авна; −1 ≤; −1 ≤ r ≤ 1.r ≤ 1.
• 3.3. Тэгш хэмтэй байнаТэгш хэмтэй байна;; XX баба Y(rY(rXYXY)) хоорондын корреляцийнхоорондын корреляцийн
коэффициент нькоэффициент нь YY баба X(rX(rYXYX)) хоорондынхтой адил байнахоорондынхтой адил байна..
• 4.4. Эх хувьсагчид болон хэмжээсийн хувьд бие даасан байнаЭх хувьсагчид болон хэмжээсийн хувьд бие даасан байна;; хэрэвхэрэв
X*X*ii = aX= aXii + C+ C баба Y*Y*ii = bY= bYii + d,+ d, эндэнд a > 0, b > 0,a > 0, b > 0, болонболон cc баба dd нь тогтмолнь тогтмол, X*, X*
баба Y*Y* хоорондоххоорондох rr нь эх хувьсагчид болох Х ба -ийн хоорондохҮнь эх хувьсагчид болох Х ба -ийн хоорондохҮ rr--
тай адил байна.тай адил байна.
• 5.5. ХэрэвХэрэв XX баба YY ньнь статистик хамааралг й болүстатистик хамааралг й болү тэдгээрийнтэдгээрийн
хоорондын корреляцийн коэффициент тэг байнахоорондын корреляцийн коэффициент тэг байна;; гэвч хэрэвгэвч хэрэв r = 0r = 0
нь хоёр хавьсагч хамааралг йг илэрхийлэхг йү үнь хоёр хавьсагч хамааралг йг илэрхийлэхг йү ү ..
• 6.6. Энэ нь з вх н шугаман хамаарлыг хэмждэгө өЭнэ нь з вх н шугаман хамаарлыг хэмждэгө ө ;; шугаман бусшугаман бус
хамаарлыг илэрхийлэхг йүхамаарлыг илэрхийлэхг йү ..
• 7.7. Хэдийгээр энэ нь хоёр хувьсагчийн шугаман хамаарлынХэдийгээр энэ нь хоёр хувьсагчийн шугаман хамаарлын
хэмжигдэх н боловчүүхэмжигдэх н боловчүү ямар нэг учир шалтгааны н л гө өөямар нэг учир шалтгааны н л гө өө
илэрхийлэхг йүилэрхийлэхг йү ..

59. • Регрессийн х рээнд авч звэлү үРегрессийн х рээнд авч звэлү ү rr22
ньнь rr-с ил утга учиртайүү-с ил утга учиртайүү
хэмжигдэх н б г д тайлбарлагч хувьсагчдаар тайлбарлагдахүү ө өөхэмжигдэх н б г д тайлбарлагч хувьсагчдаар тайлбарлагдахүү ө өө
хамааран хувьсагчийн хэлбэлзлийн хувь буюу нэг хувьсагчийнхамааран хувьсагчийн хэлбэлзлийн хувь буюу нэг хувьсагчийн
хэлбэлзэл нь н г хувьсагчийн хэлбэлзлийг тодорхойлдогө өөхэлбэлзэл нь н г хувьсагчийн хэлбэлзлийг тодорхойлдогө өө
ер нхий хэмжигдэх н юмө үүер нхий хэмжигдэх н юмө үү .. нээс гадна олон хэмжээстҮүнээс гадна олон хэмжээстҮү
регрессийн загвартрегрессийн загварт r (= R)r (= R)-ийн тайлбар эргэлзээтэй утга-ийн тайлбар эргэлзээтэй утга
илэрхийлдгийг бид харах болно.илэрхийлдгийг бид харах болно. ДашрамдДашрамд,, мн тодорхойлсонө өмн тодорхойлсонө ө rr22
ньнь
бодитбодит YYii болон нэлэгдсэнүболон нэлэгдсэнү YˆYˆii хоорондын корреляцийнхоорондын корреляцийн
коэффициентийг квадрат зэрэг дэш лэн тооцож болдог.үүкоэффициентийг квадрат зэрэг дэш лэн тооцож болдог.үү
(3.5.13)(3.5.13)-г ашиглан бид дараах байдлаар бичиж болно-г ашиглан бид дараах байдлаар бичиж болно

60. • эндэнд YYii == бодитбодит Y, YˆY, Yˆii == нэлсэнүнэлсэнү Y,Y, баба Y¯ = Y¯ˆ = YY¯ = Y¯ˆ = Y-ийн дундаж-ийн дундаж..
Баталгааг дасгалБаталгааг дасгал 3.153.15-с хар-с хар. (3.5.14). (3.5.14) илэрхийлэл нэлсэн утгуудү Үилэрхийлэл нэлсэн утгуудү Ү
тэдгээрийн бодит утгуудтай хэр ойр байгаа буюу нийцтэйтэдгээрийн бодит утгуудтай хэр ойр байгаа буюу нийцтэй
байдлын хэмжигдэх н болохүүбайдлын хэмжигдэх н болохүү rr22
–ийн тодорхойлолтыг–ийн тодорхойлолтыг
з втг д г.ө ө өз втг д г.ө ө ө

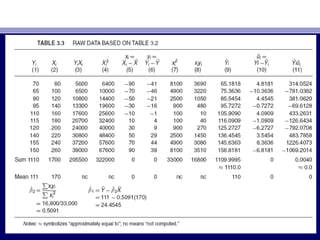
61. Тоон жишээ

62. • βˆβˆ11 = 24.4545= 24.4545 var (var (βˆβˆ11) = 41.1370) = 41.1370 баба se (se (βˆβˆ11) = 6.4138) = 6.4138
• βˆβˆ22 = 0.5091= 0.5091 var (var (βˆβˆ22) = 0.0013) = 0.0013 баба se (se (βˆβˆ22) = 0.0357) = 0.0357
• cov (cov (βˆβˆ11, βˆ, βˆ22) = −0.2172) = −0.2172 σˆσˆ22
= 42.1591= 42.1591 (3.6.1)(3.6.1)
• rr22
= 0.9621= 0.9621 r = 0.9809r = 0.9809 df = 8df = 8
• нэлэгдсэн регрессийн шулуун ньҮнэлэгдсэн регрессийн шулуун ньҮ
• YˆYˆii = 24.4545 + 0.5091X= 24.4545 + 0.5091Xii (3.6.2)(3.6.2)
• Геометрийн хувьд зурагГеометрийн хувьд зураг 3.123.12-т харуулсан-т харуулсан..
• Б лэгүБ лэгү 22-ийн дагуу-ийн дагуу SRF [SRF [ТэгшитгэлТэгшитгэл (3.6.2)](3.6.2)] ба т нтэй холбоотойүүба т нтэй холбоотойүү
регрессийн шулуун нь дараах байдлаар тайлбарлагддагрегрессийн шулуун нь дараах байдлаар тайлбарлагддаг::
Регрессийн шулуун дээрх цэг б р нь г гдс н Х утгад харгалзах -ү ө ө ө ҮРегрессийн шулуун дээрх цэг б р нь г гдс н Х утгад харгалзах -ү ө ө ө Ү
ийн дундаж утгын нэлэлт,үийн дундаж утгын нэлэлт,ү YˆYˆii ньнь E(Y | XE(Y | Xii))-ийн нэлэлтү-ийн нэлэлтү . βˆ. βˆ22 = 0.5091= 0.5091
утгаутга нь шулууны налалтыг хэмждэг ба Х долоо хоногтнь шулууны налалтыг хэмждэг ба Х долоо хоногт $80$80--$260$260
хоорондхооронд $1$1-р с х д дундаж хэрэглээний зардал 51 центээр снө ө ө ө ө-р с х д дундаж хэрэглээний зардал 51 центээр снө ө ө ө ө..
βˆβˆ11 = 24.4545= 24.4545 утга нь шулууны тогтмол коэффициент б г дө өөутга нь шулууны тогтмол коэффициент б г дө өө
долоо хоногийн орлого тэг байхад долоо хоногийн хэрэглээнийдолоо хоногийн орлого тэг байхад долоо хоногийн хэрэглээний
зардлын дундаж т вшинг илэрхийлнэ.үзардлын дундаж т вшинг илэрхийлнэ.ү

65. • Хэдийгээр энэ нь тогтмол коэффициентийн механик тайлбарХэдийгээр энэ нь тогтмол коэффициентийн механик тайлбар
боловчболовч.. Регрессийн шинжилгээнд тогтмол параметрийн гчилсэнүРегрессийн шинжилгээнд тогтмол параметрийн гчилсэнү
тайлбар нь ргэлж утга илэрхийлэхг й байж болох ба хэдий энэү үтайлбар нь ргэлж утга илэрхийлэхг й байж болох ба хэдий энэү ү
жишээнд орлогог й гэр б лү үжишээнд орлогог й гэр б лү ү ((ажилг йүажилг йү ,, ажлаас халагдсан гэх мэтажлаас халагдсан гэх мэт
шалтгаанааршалтгаанаар)) зээл авах, зардал нь орлогоосоо давах зэргээрзээл авах, зардал нь орлогоосоо давах зэргээр
хэрэглээний зардлын минимум т вшинг илэрхийлж болох юм.үхэрэглээний зардлын минимум т вшинг илэрхийлж болох юм.ү
Гэвч ер нхийд тогтмол параметрийг тайлбарлах нийтлэгө өөГэвч ер нхийд тогтмол параметрийг тайлбарлах нийтлэгө өө
мэдрэмжийг ашиглавал ажиглалтын Х утгуудын т врийнүүмэдрэмжийг ашиглавал ажиглалтын Х утгуудын т врийнүү
х рээнд ихэвчлэн тэг утга байхг й байдагү үх рээнд ихэвчлэн тэг утга байхг й байдагү ү .. Магадг йүМагадг йү тогтмолтогтмол
параметрийн хамгийн сайн тайлбар нь регрессийн загвартпараметрийн хамгийн сайн тайлбар нь регрессийн загварт
орхигдсон б х хувьсагчдын -т з лэх дундаж н л гү Ү ү үү ө өөорхигдсон б х хувьсагчдын -т з лэх дундаж н л гү Ү ү үү ө өө
илэрхийлнэ гэж зэж болох юм.үилэрхийлнэ гэж зэж болох юм.ү rr22
ньнь 0.96210.9621 бол орлогоорбол орлогоор
тайлбарлагдах долоо хоногийн хэрэглээний зардлын хэлбэлзэлтайлбарлагдах долоо хоногийн хэрэглээний зардлын хэлбэлзэл 9696
хувь гэж знэүхувь гэж знэү .. rr22
11-р д х х тусам т врийн регрессийн шулуунүү ө ө үү-р д х х тусам т врийн регрессийн шулуунүү ө ө үү
г гд лд маш сайн нийцтэй байгааг илэрхийлнэө ө өг гд лд маш сайн нийцтэй байгааг илэрхийлнэө ө ө .. КорреляцийнКорреляцийн
коэффициенткоэффициент 0.98090.9809 нь хэрэглээний зардал болон орлого ньнь хэрэглээний зардал болон орлого нь
х чтэй эерэг хамааралтайг харуулна. Регрессийнүх чтэй эерэг хамааралтайг харуулна. Регрессийнү
коэффициентийн нэлэгдсэн стандарт алдааг Б лэгү үкоэффициентийн нэлэгдсэн стандарт алдааг Б лэгү ү 55-д авч знэү-д авч знэү ..

66. • 3.1-3.33.1-3.3 дэх тоон жишээг хардэх тоон жишээг хар