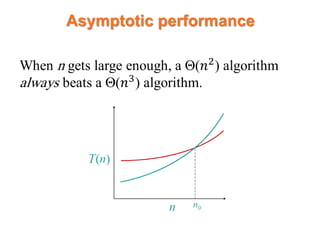
This course introduces students to analyzing and designing computer algorithms. The course objectives are to analyze asymptotic performance, demonstrate familiarity with major algorithms and data structures, apply algorithm design paradigms and analysis methods, and synthesize efficient algorithms for engineering problems. Topics covered include foundations of algorithms, accuracy, efficiency, comparing efficiencies, and understanding various algorithm variants and their design and analysis.