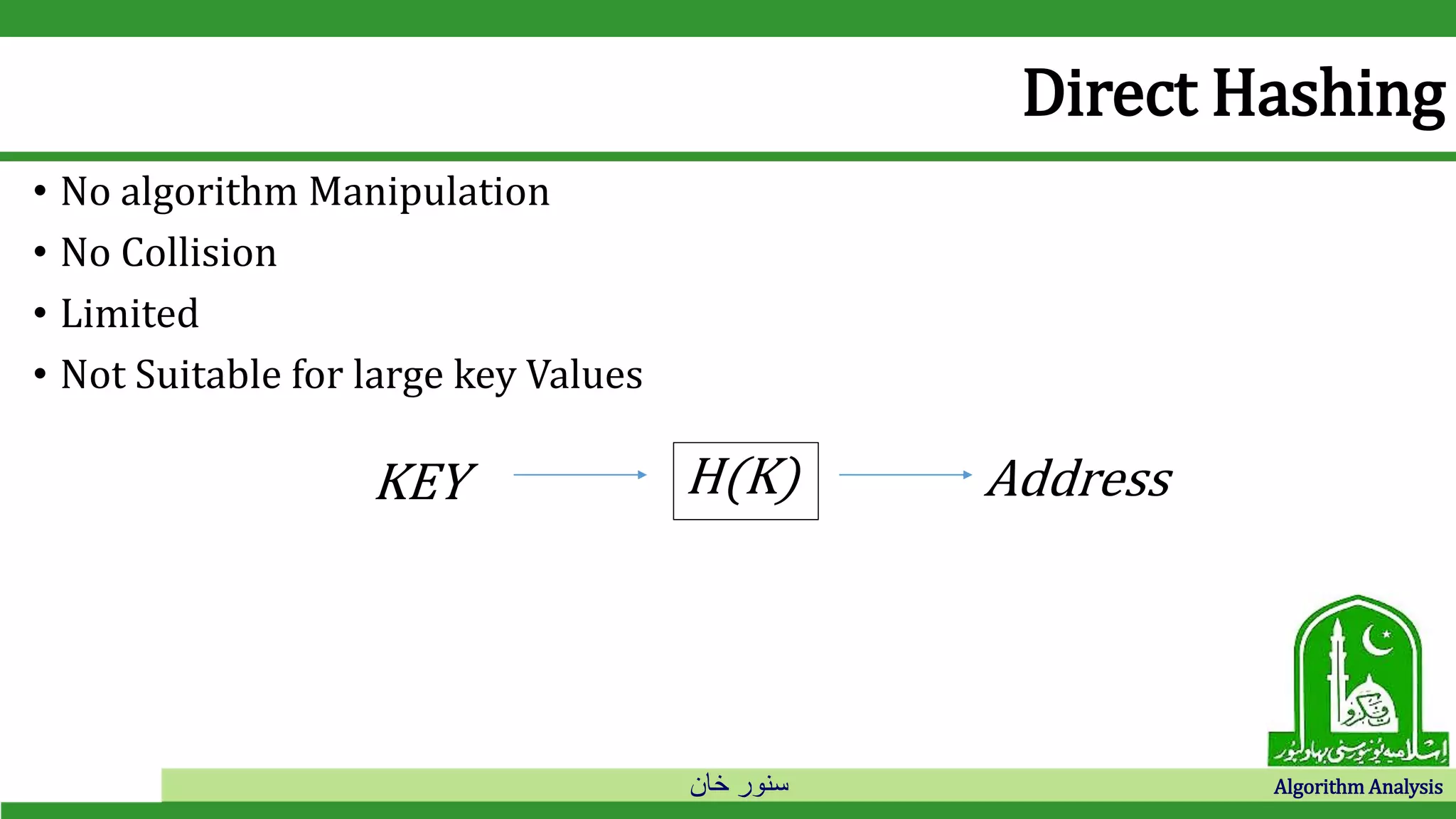
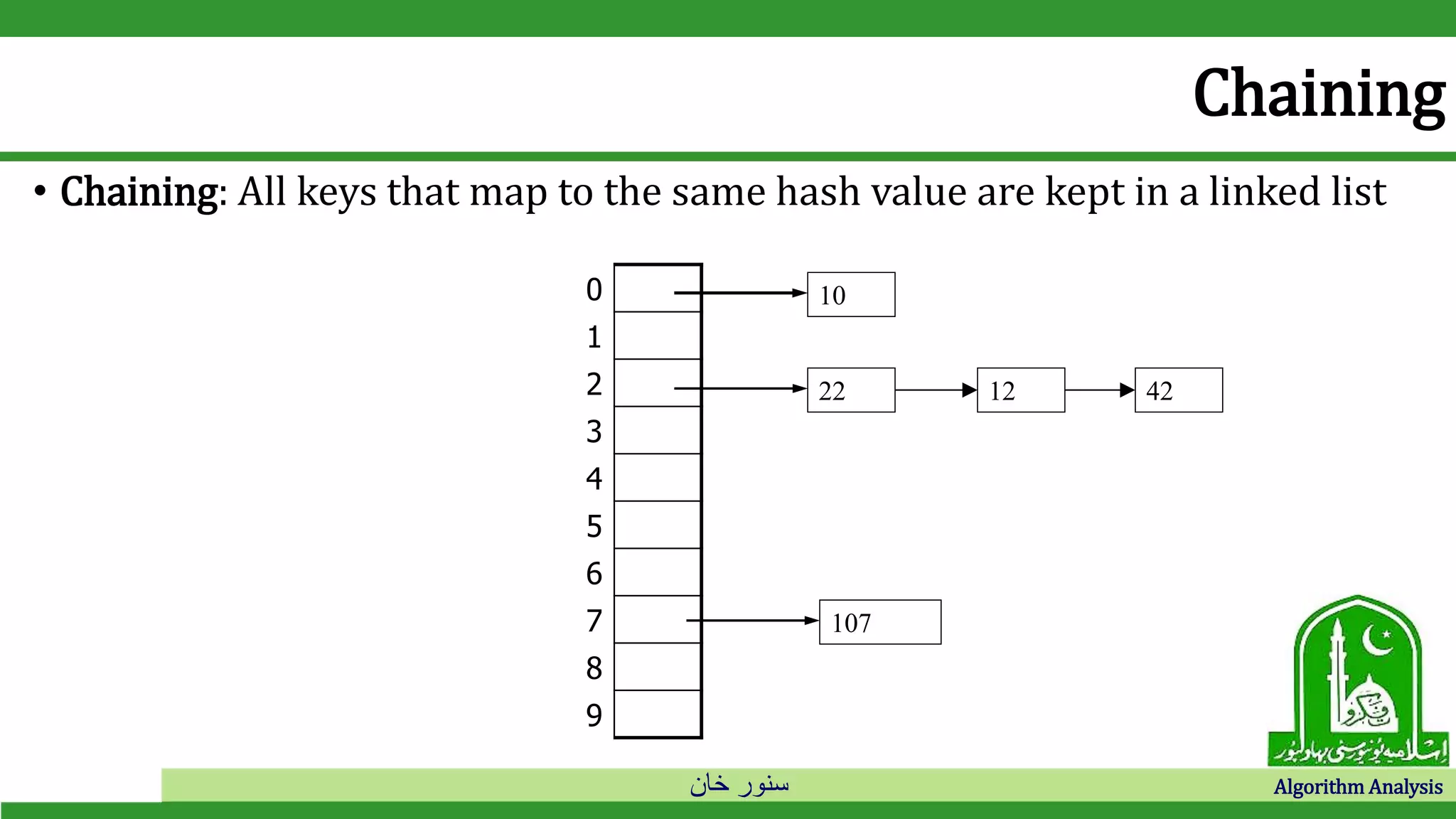
The document discusses hash tables and collision resolution techniques for hash tables. It defines hash tables as an implementation of dictionaries that use hash functions to map keys to array slots. Collisions occur when multiple keys hash to the same slot. Open addressing techniques like linear probing and quadratic probing search the array sequentially for empty slots when collisions occur. Separate chaining creates an array of linked lists so items can be inserted into lists when collisions occur.






![خان سنور Algorithm Analysis
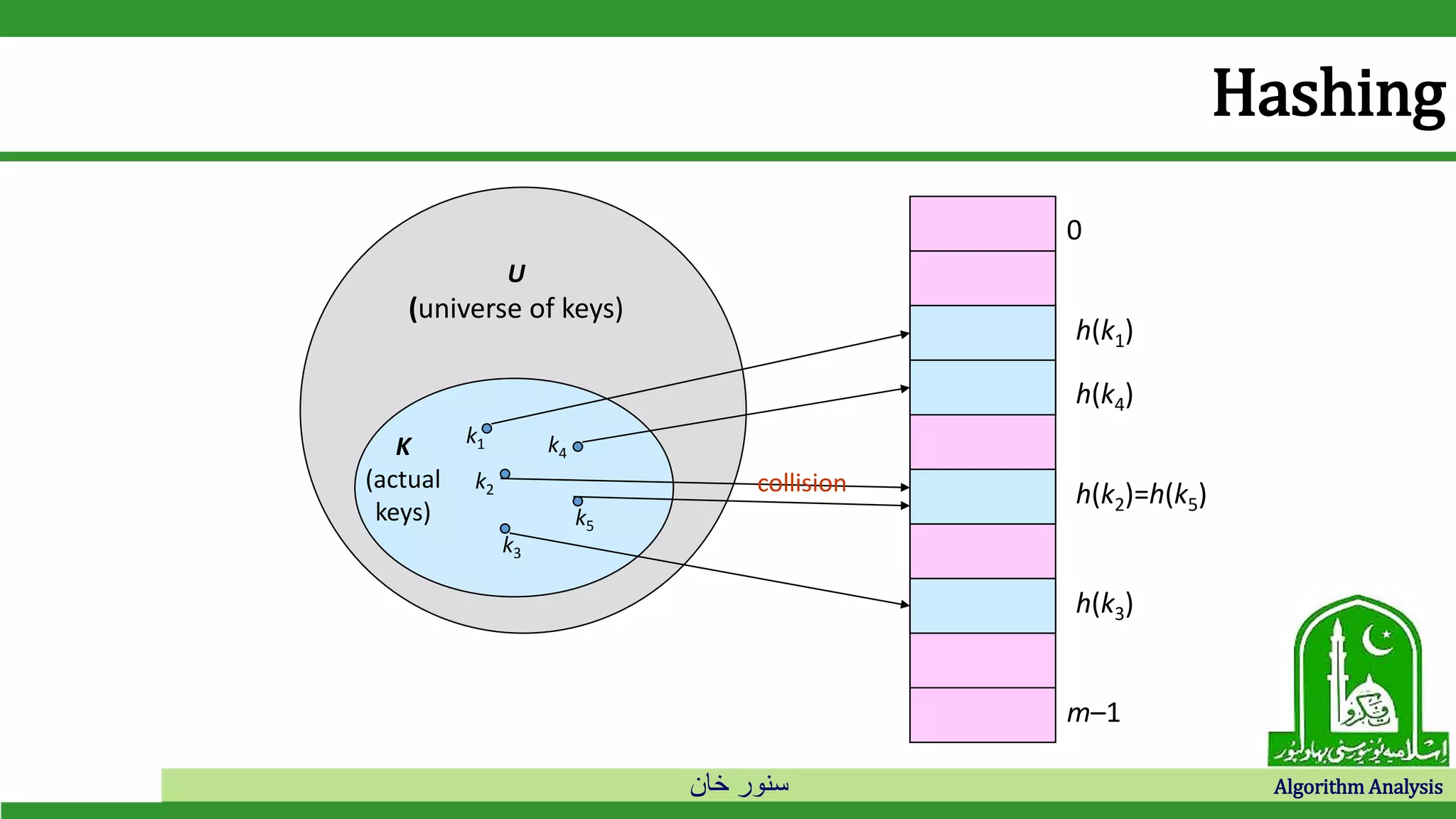
Hashing
• Hash function h: Mapping from U to the slots of a hash table T[0..m–1].
h : U {0,1,…, m–1}
• With arrays, key k maps to slot A[k].
• With hash tables, key k maps or “hashes” to slot T[h[k]].
• h[k] is the hash value of key k.](https://image.slidesharecdn.com/hashtables-190528012409/75/Hash-tables-7-2048.jpg)

![خان سنور Algorithm Analysis
What is a Hash Table ?
• The simplest kind of hash
table is an array of records.
• This example has 701
records.
[ 0 ] [ 1 ] [ 2 ] [ 3 ] [ 4 ] [ 5 ]
An array of records
. . .
[ 700]](https://image.slidesharecdn.com/hashtables-190528012409/75/Hash-tables-10-2048.jpg)
![خان سنور Algorithm Analysis
What is a Hash Table ?
• Each record has a special
field, called its key.
• In this example, the key is
a long integer field called
Number.
[ 0 ] [ 1 ] [ 2 ] [ 3 ] [ 4 ] [ 5 ]
. . .
[ 700]
[ 4 ]
Number 506643548](https://image.slidesharecdn.com/hashtables-190528012409/75/Hash-tables-11-2048.jpg)
![خان سنور Algorithm Analysis
What is a Hash Table ?
• The number might be a
person's identification
number, and the rest of the
record has information
about the person.
[ 0 ] [ 1 ] [ 2 ] [ 3 ] [ 4 ] [ 5 ]
. . .
[ 700]
[ 4 ]
Number 506643548](https://image.slidesharecdn.com/hashtables-190528012409/75/Hash-tables-12-2048.jpg)
![خان سنور Algorithm Analysis
What is a Hash Table ?
• When a hash table is in use,
some spots contain valid
records, and other spots are
"empty".
[ 0 ] [ 1 ] [ 2 ] [ 3 ] [ 4 ] [ 5 ] [ 700]
Number 506643548Number 233667136Number 281942902
Number 155778322
. . .](https://image.slidesharecdn.com/hashtables-190528012409/75/Hash-tables-13-2048.jpg)
![خان سنور Algorithm Analysis
Inserting a New Record
• In order to insert a new
record, the key must
somehow be converted to an
array index.
• The index is called the hash
value of the key.
[ 0 ] [ 1 ] [ 2 ] [ 3 ] [ 4 ] [ 5 ] [ 700]
Number 506643548Number 233667136Number 281942902
Number 155778322
. . .
Number 580625685](https://image.slidesharecdn.com/hashtables-190528012409/75/Hash-tables-14-2048.jpg)
![خان سنور Algorithm Analysis
Inserting a New Record
• Typical way create a hash
value:
[ 0 ] [ 1 ] [ 2 ] [ 3 ] [ 4 ] [ 5 ] [ 700]
Number 506643548Number 233667136Number 281942902
Number 155778322
. . .
Number 580625685
(Number mod 701)
What is (580625685 mod 701) ?](https://image.slidesharecdn.com/hashtables-190528012409/75/Hash-tables-15-2048.jpg)
![خان سنور Algorithm Analysis
Inserting a New Record
• Typical way to create a hash
value:
[ 0 ] [ 1 ] [ 2 ] [ 3 ] [ 4 ] [ 5 ] [ 700]
Number 506643548Number 233667136Number 281942902
Number 155778322
. . .
Number 580625685
(Number mod 701)
What is (580625685 mod 701) ?
3](https://image.slidesharecdn.com/hashtables-190528012409/75/Hash-tables-16-2048.jpg)
![خان سنور Algorithm Analysis
Inserting a New Record
• The hash value is used for
the location of the new
record.
Number 580625685
[ 0 ] [ 1 ] [ 2 ] [ 3 ] [ 4 ] [ 5 ] [ 700]
Number 506643548Number 233667136Number 281942902
Number 155778322
. . .
[3]](https://image.slidesharecdn.com/hashtables-190528012409/75/Hash-tables-17-2048.jpg)
































![خان سنور Algorithm Analysis52
• Average case analysis of search, with linear probing:
• Number of lookups worse than chaining
• Complicated to analyze; done by Knuth [1962]
• unsuccessful:
• successful:
Analysis of hash table search
2
)1(
1
1
2
1
1
1
1
2
1](https://image.slidesharecdn.com/hashtables-190528012409/75/Hash-tables-52-2048.jpg)


![خان سنور Algorithm Analysis
Exam Related Questions
11.1-2
A bit vector is simply an array of bits(0sand 1s). A bit vector of length m takes much
less space than an array of m pointers. Describe how to use a bit vector to represent a
dynamic set of distinct elements with no satellite data. Dictionary operations should
run in O.1/ time.
Answer
Start with a bit vector b which contains a 1 in position k if k is in the dynamic set, and
a 0 otherwise. To search, we return true if b[x]==1. To insert x, set b[x]=1. To delete
x, set b[x]=0. Each of the set takes O(1)time.](https://image.slidesharecdn.com/hashtables-190528012409/75/Hash-tables-55-2048.jpg)



![خان سنور Algorithm Analysis
Exam Related Questions
11.4-2
Write pseudo code for HASH-DELETE as outlined in the text, and modify HASH-
INSERT to handle the special value DELETED.
Answer
i = HASH SEARCH(T;k)
T[i]= DELETED
We modify INSERT by changing line 4 to: if T[j]== NIL or T[j]== DELETED.
Algorithm1 HASH-DELETE(T,k)](https://image.slidesharecdn.com/hashtables-190528012409/75/Hash-tables-59-2048.jpg)