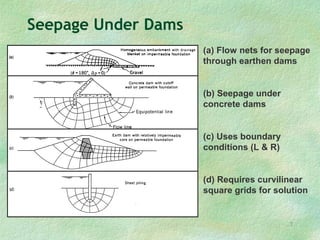
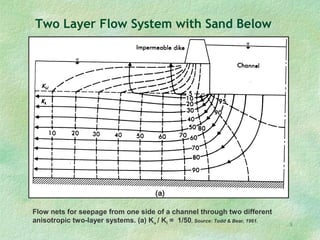
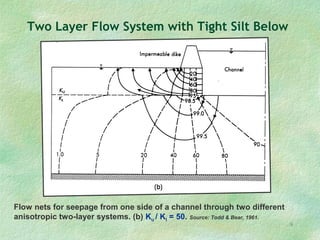
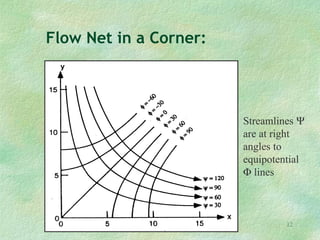
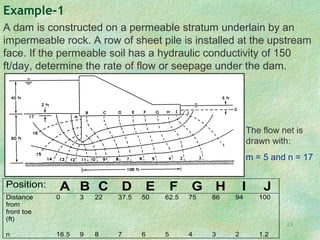
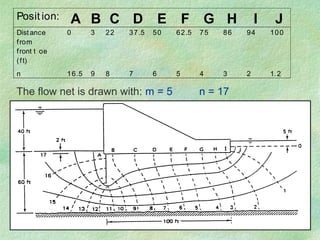
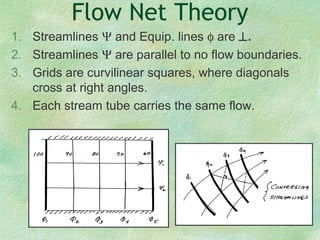
Flow net theory describes the graphical representation of groundwater flow through porous media. Flow nets show streamlines perpendicular to equipotential lines forming curvilinear square grids. They can model flow under dams, through layered soils, and with different boundary conditions. Examples calculate seepage rates from flow net parameters like hydraulic conductivity, head loss, number of streamlines and equipotential lines.

1. Flow Nets
• Flow Net Theory
• Flow Net in Isotropic Soil
• Drawing Method
• Seepage Under Dams
• Effects of Boundary Condition on Shape of Flow Nets
• Examples

2. 2
Flow Net Theory
1. Streamlines Ψ and Equip. lines φ are ⊥.
2. Streamlines Ψ are parallel to no flow boundaries.
3. Grids are curvilinear squares, where diagonals
cross at right angles.
4. Each stream tube carries the same flow.

3. 3
Flow Net in Isotropic Soil
 Portion of a flow net is shown below
 The equation for flow nets originates from Darcy’s Law.
 Flow Net solution is equivalent to solving the governing
equations of flow for a uniform isotropic aquifer with well-
defined boundary conditions.
Φ
Ψ
Stream tube

4. 4
 Flow through a channel between equipotential lines φ1 and φ2
per unit width is:
∆q = K(dm x 1)(∆h1/dl)
 Flow through equipotential lines 2 and 3 is:
∆q = K(dm x 1)(∆h2/dl)
 The flow net has square grids, so the head drop is the same in
each potential drop: ∆h1 = ∆h2
 If there are n such drops, then: ∆h = (H/n)
where H is the total head loss between the first and last
equipotential lines.

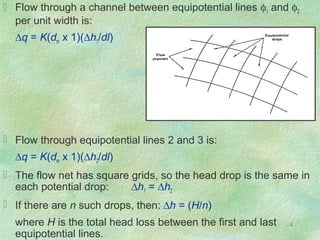
5. 5
 Substitution yields: ∆q = K(dm/dl)(H/n)
 This equation is for one flow channel. If there are m such
channels in the net, then total flow per unit width is:
q = (m/n)K(dm/dl)H
 Since the flow net is drawn with squares, then dm ≈ dl, and:
q = (m/n)KH [L2
T-1
]
where:
q = rate of flow or seepage per unit width
m= number of flow channels
n= number of equipotential drops
h = total head loss in flow system
K = hydraulic conductivity

6. 6
Drawing Method:
1. Draw to a convenient scale the cross sections of the structure, water
elevations, and aquifer profiles.
2. Establish boundary conditions and draw one or two flow lines Ψ and
equipotential lines Φ near the boundaries.
3. Sketch intermediate flow lines and equipotential lines by smooth
curves adhering to right-angle intersections and square grids. Where
flow direction is a straight line, flow lines are an equal distance apart
and parallel.
4. Continue sketching until a problem develops. Each problem will
indicate changes to be made in the entire net. Successive trials will
result in a reasonably consistent flow net.
5. In most cases, 5 to 10 flow lines are usually sufficient. Depending on
the no. of flow lines selected, the number of equipotential lines will
automatically be fixed by geometry and grid layout.
6. Equivalent to solving the governing equations of GW flow in 2-
dimensions.

7. 7
Seepage Under Dams
(a) Flow nets for seepage
through earthen dams
(b) Seepage under
concrete dams
(c) Uses boundary
conditions (L & R)
(d) Requires curvilinear
square grids for solution

8. 8
Two Layer Flow System with Sand Below
Flow nets for seepage from one side of a channel through two different
anisotropic two-layer systems. (a) Ku / Kl = 1/50, Source: Todd & Bear, 1961.

9. 9
Two Layer Flow System with Tight Silt Below
Flow nets for seepage from one side of a channel through two different
anisotropic two-layer systems. (b) Ku / Kl = 50. Source: Todd & Bear, 1961.

10. 10
Effects of Boundary Condition on Shape
of Flow Nets

11. 11
Radial Flow:
Contour map of the piezometric surface near Savannah, Georgia,
1957, showing closed contours resulting from heavy local
groundwater pumping (after USGS Water-Supply Paper 1611).

12. 12
Flow Net in a Corner:
Streamlines Ψ
are at right
angles to
equipotential
Φ lines

13. 13
Example-1
A dam is constructed on a permeable stratum underlain by an
impermeable rock. A row of sheet pile is installed at the upstream
face. If the permeable soil has a hydraulic conductivity of 150
ft/day, determine the rate of flow or seepage under the dam.
Position: A B C D E F G H I J
Distance
from
front toe
(ft)
0 3 22 37.5 50 62.5 75 86 94 100
n 16.5 9 8 7 6 5 4 3 2 1.2
The flow net is
drawn with:
m = 5 and n = 17

14. 14
Posit ion: A B C D E F G H I J
Dist ance
from
front t oe
(ft)
0 3 22 37.5 50 62.5 75 86 94 100
n 16.5 9 8 7 6 5 4 3 2 1.2
The flow net is drawn with: m = 5 n = 17

15. 15
The solution:
Solve for the flow per unit width:
q = (m/n) K h
= (5/17)(150)(35)
= 1544 ft3
/day per ft

16. 16
Example-2
There is an earthen dam 13 meters across and 7.5 meters high.
The Impounded water is 6.2 meters deep, while the tail water is
2.2 meters deep. The dam is 72 meters long. If the hydraulic
conductivity is 6.1 x 10-4
cm/sec, what is the seepage through the
dam if n = 21 and m = 6.
The solution:
K = 6.1 x 10-4
cm/sec = 0.527 m/day
From the flow net, the total head loss, H = 6.2 -2.2 = 4.0 meters.
There are 6 flow channels (m) and 21 head drops along each flow
path (n).
Q = (K.H.m/n) x dam length
= (0.527 m/day x 4m x 6/21) x (dam length)
= 0.60 m3
/day per m of dam = 0.6 x 72m
= 43.4 m3
/day for the entire 72-meter length of the