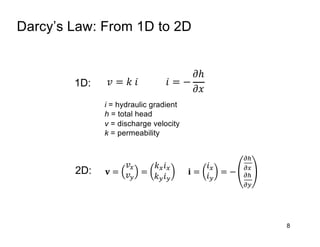
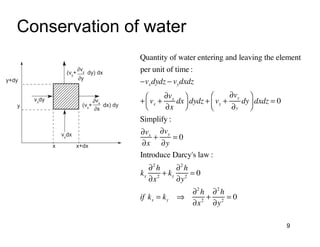
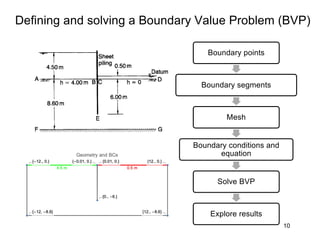
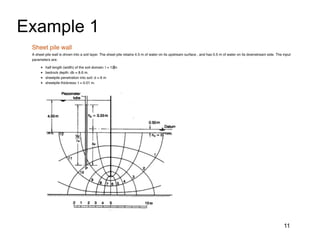
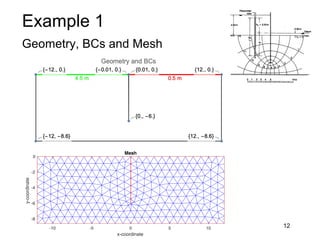
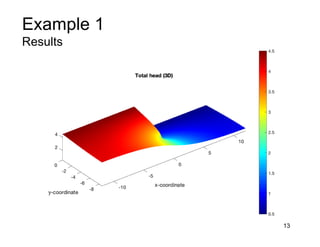
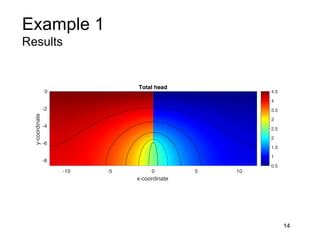
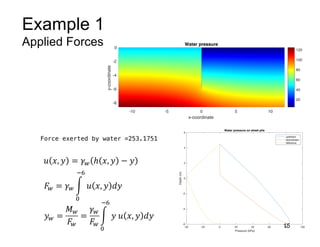
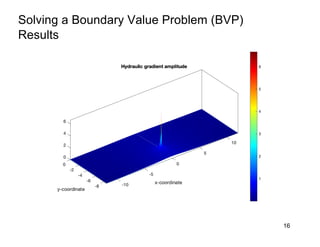
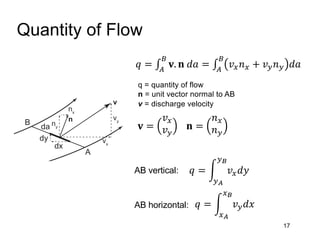
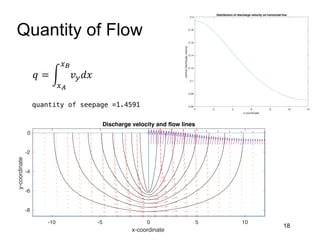
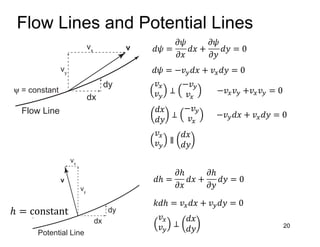
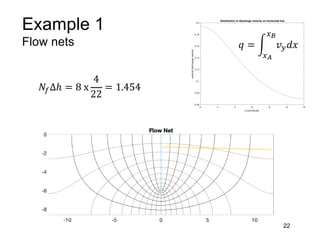
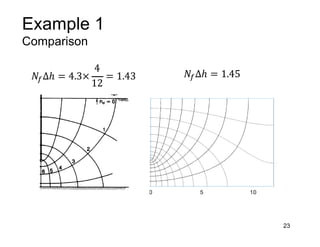
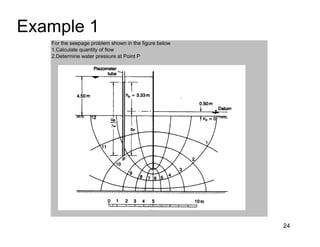
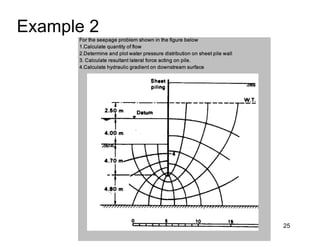
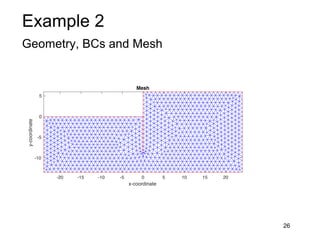
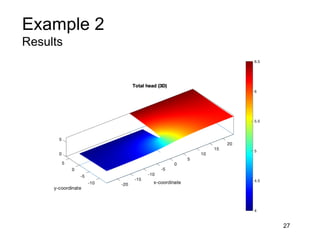
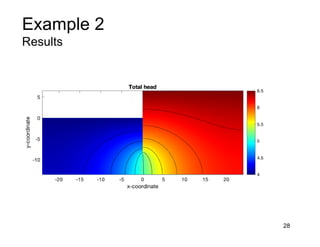
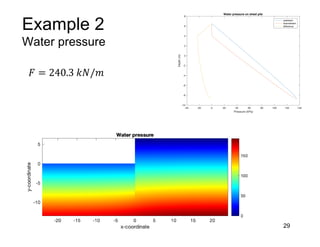
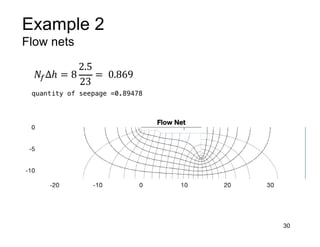
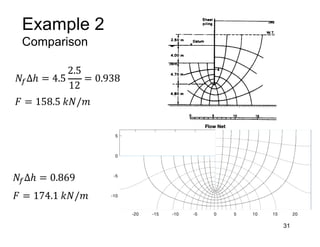
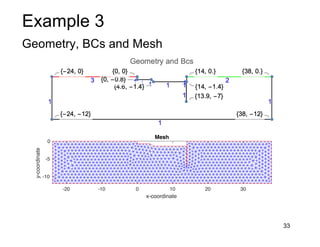
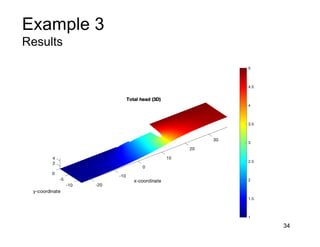
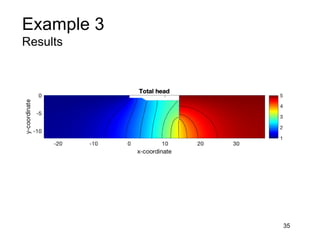
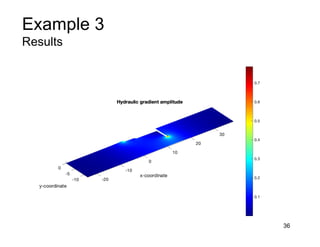
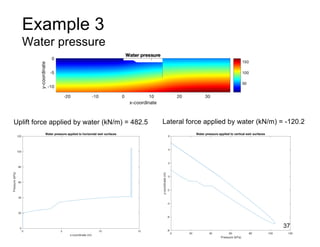
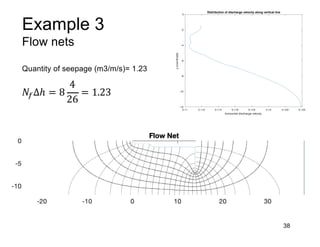
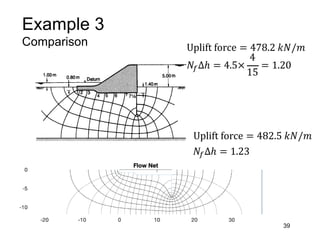
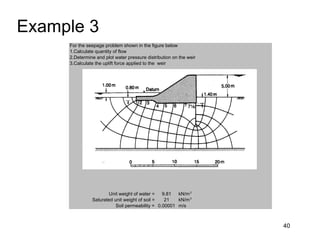
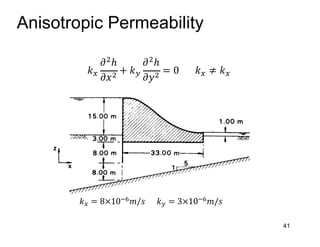
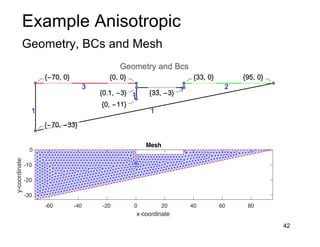
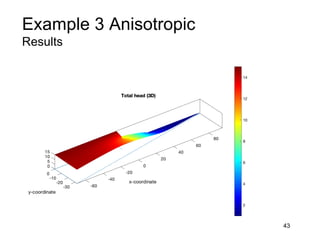
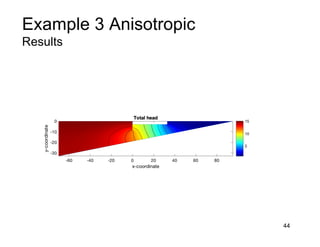
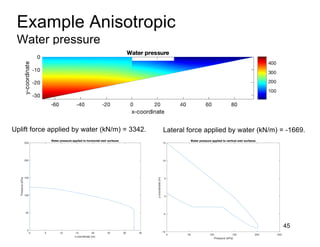
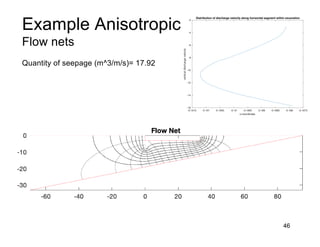
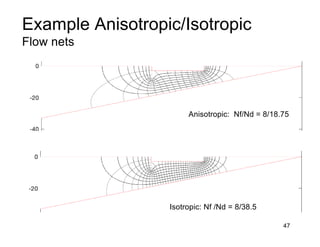
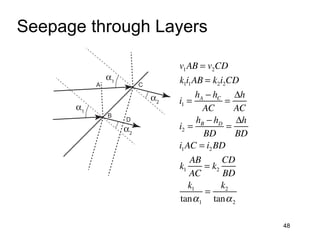
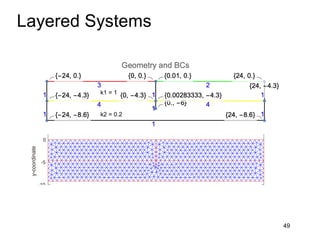
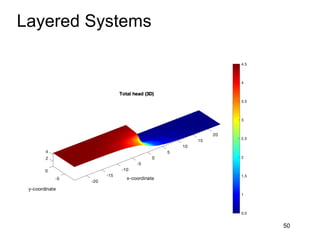
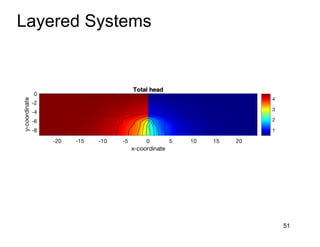
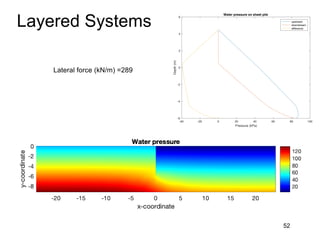
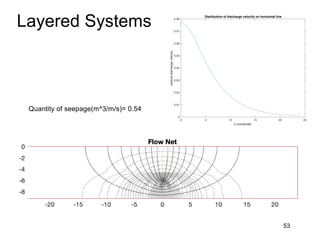
This document provides an overview and examples of seepage analysis through soils. It begins by defining key concepts like Darcy's law, which describes water flow through porous media. It then discusses how to formulate seepage as a boundary value problem by defining geometry, boundary conditions, and the governing equation. The document provides examples of using finite element methods to solve example problems, producing results like flow nets, water pressures, and forces. It also covers topics like anisotropic permeability and comparing isotropic and anisotropic cases.

1. CE 470
Foundations and
Earth Retaining Systems
Seepage
Jean-Pierre Bardet
University of Miami

2. 2
Learning Objectives
1. Identify examples of real seepage problems
2. Define the equation governing how water
seeps through soils
3. Formulate seepage as a boundary value
problem
4. Overview finite elements methods for solving
seepage boundary value problems
5. Apply computational results, i.e., flow nets, to
obtain engineering quantities:
• quantity of seepage
• pressure and forces, and
• hydraulic gradients

3. Sheet Pile Walls

4. Sheet Pile Walls

5. Sheet Pile Walls

6. Sheet Pile Walls

7. Weirs

8. Darcy’s Law: From 1D to 2D
8
𝐯 =
𝑣!
𝑣"
=
𝑘!𝑖!
𝑘"𝑖"
𝐢 =
𝑖!
𝑖"
= −
#$
#!
#$
#"
𝑣 = 𝑘 𝑖 𝑖 = −
𝜕ℎ
𝜕𝑥
1D:
2D:
i = hydraulic gradient
h = total head
v = discharge velocity
k = permeability

9. Conservation of water
9
Quantity of water entering and leaving the element
per unit of time :
−vxdydz − vydxdz
+ vx +
∂vx
∂x
dx
⎛
⎝
⎜
⎞
⎠
⎟ dydz + vy +
∂vy
∂y
dy
⎛
⎝
⎜
⎞
⎠
⎟ dxdz = 0
Simplify :
∂vx
∂x
+
∂vy
∂y
= 0
Introduce Darcy's law :
kx
∂2
h
∂x2
+ ky
∂2
h
∂y2
= 0
if kx = ky ⇒
∂2
h
∂x2
+
∂2
h
∂y2
= 0
x x+dx
y+dy
y
(vy
+ dy) dx
∂vy
∂y
(vx
+ dx) dy
∂vx
∂x
vy
dx
vx
dy

10. Defining and solving a Boundary Value Problem (BVP)
10
Boundary points
Boundary segments
Mesh
Boundary conditions and
equation
Solve BVP
Explore results

11. Example 1
11

12. Example 1
Geometry, BCs and Mesh
12
-10 -5 0 5 10
x-coordinate
-8
-6
-4
-2
0
y-coordinate
Mesh

13. Example 1
Results
13

14. Example 1
Results
14
-10 -5 0 5 10
x-coordinate
-8
-6
-4
-2
0
y-coordinate
Total head
0.5
1
1.5
2
2.5
3
3.5
4
4.5

15. -40 -20 0 20 40 60 80 100
Pressure (kPa)
-6
-4
-2
0
2
4
6
Depth
(m)
Water pressure on sheet pile
upstream
downstream
difference
Example 1
Applied Forces
15
𝑢 𝑥, 𝑦 = 𝛾% ℎ 𝑥, 𝑦 − 𝑦
𝐹
% = 𝛾% /
&
'(
𝑢 𝑥, 𝑦 𝑑𝑦
𝑦% =
𝑀%
𝐹
%
=
𝛾%
𝐹
%
/
&
'(
𝑦 𝑢 𝑥, 𝑦 𝑑𝑦
-10 -5 0 5 10
x-coordinate
-8
-6
-4
-2
0
y-coordinate
Water pressure
20
40
60
80
100
120

16. Solving a Boundary Value Problem (BVP)
Results
16

17. Quantity of Flow
17
vy
vx
v
ψ = ψA
Flow Line
A
B ny
nx
n
da
dx
dy
𝑞 = ∫
!
"
𝐯. 𝐧 𝑑𝑎 = ∫
!
"
𝑣#𝑛# + 𝑣$𝑛$ 𝑑𝑎
q = quantity of flow
n = unit vector normal to AB
v = discharge velocity
𝐯 =
𝑣#
𝑣$
𝐧 =
𝑛#
𝑛$
𝑞 = 2
$)
$*
𝑣#𝑑𝑦
𝑞 = 2
#)
#*
𝑣$𝑑𝑥
AB vertical:
AB horizontal:

18. Quantity of Flow
18
-10 -5 0 5 10
x-coordinate
-8
-6
-4
-2
0
y-coordinate
Discharge velocity and flow lines
0 2 4 6 8 10 12
x-coordinate
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
vertical
discharge
velocty
Distribution of discharge velocity on horizontal line
𝑞 = 2
#)
#*
𝑣$𝑑𝑥

19. Flow Net – Flow Function
19
𝑘#
𝜕%
ℎ
𝜕𝑥%
+ 𝑘$
𝜕%
ℎ
𝜕𝑦%
= 0 𝑘# ≠ 𝑘#
𝑣# = −𝑘#
𝜕ℎ
𝜕𝑥
= −
𝜕𝜓
𝜕𝑦
𝑣$= −𝑘$
𝜕ℎ
𝜕𝑦
=
𝜕𝜓
𝜕𝑥
𝑑𝜓 =
𝜕𝜓
𝜕𝑥
𝑑𝑥 +
𝜕𝜓
𝜕𝑦
𝑑𝑦 = 𝑣$𝑑𝑥 − 𝑣#𝑑𝑦 = 0
𝑘#
𝜕%𝜓
𝜕𝑥%
+ 𝑘$
𝜕%𝜓
𝜕𝑥%
= 0
𝜕%𝜓
𝜕𝑥%
= −𝑘$
𝜕%ℎ
𝜕𝑥𝜕𝑦
𝜕%𝜓
𝜕𝑦%
= 𝑘#
𝜕%ℎ
𝜕𝑥𝜕𝑦

20. Flow Lines and Potential Lines
20
𝑑𝜓 =
𝜕𝜓
𝜕𝑥
𝑑𝑥 +
𝜕𝜓
𝜕𝑦
𝑑𝑦 = 0
dx
vy
vx
dy
Flow Line
v
ψ = constant
𝑑𝜓 = −𝑣"𝑑𝑥 + 𝑣!𝑑𝑦 = 0
𝑣!
𝑣"
⊥
−𝑣"
𝑣!
−𝑣!𝑣" +𝑣!𝑣" = 0
𝑑𝑥
𝑑𝑦
⊥
−𝑣"
𝑣!
−𝑣"𝑑𝑥 + 𝑣!𝑑𝑦 = 0
𝑣!
𝑣"
∥
𝑑𝑥
𝑑𝑦
dx
vy
vx
dy
Potential Line
v
φ = constant
ℎ = constant
𝑑ℎ =
𝜕ℎ
𝜕𝑥
𝑑𝑥 +
𝜕ℎ
𝜕𝑦
𝑑𝑦 = 0
𝑘𝑑ℎ = 𝑣!𝑑𝑥 + 𝑣"𝑑𝑦 = 0
𝑣!
𝑣"
⊥
𝑑𝑥
𝑑𝑦

21. Increments of Flow Function and Total Head
21
ℎ − ∆ℎ
ℎ
𝜓
"
=
𝜓
!
+
∆𝜓
𝑥
𝜓
!
𝑦
𝑣$
∆𝑞 = 2
#)
#* 𝜕𝜓
𝜕𝑥
𝑑𝑥 = 𝜓" − 𝜓! = ∆𝜓
𝑥! 𝑥"
∆𝑞 = 2
#)
#*
−𝑘
𝜕ℎ
𝜕𝑦
𝑑𝑥 = 𝑘
∆ℎ
𝑦& −𝑦!
𝑥" − 𝑥! = 𝑘∆ℎ
𝑦!
𝑦&
square: 𝑦&−𝑦!= 𝑥" − 𝑥!
∆𝑞 = 2
#)
#*
𝑣$𝑑𝑥
𝑣$ = −𝑘
𝜕ℎ
𝜕𝑦
= 𝑘
∆ℎ
𝑦& −𝑦!
∆𝑞 = ∆𝜓 = 𝑘∆ℎ

22. Example 1
Flow nets
22
𝑁'∆ℎ = 8 x
4
22
= 1.454
0 2 4 6 8 10 12
x-coordinate
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
vertical
discharge
velocty
Distribution of discharge velocity on horizontal line
𝑞 = 2
#)
#*
𝑣$𝑑𝑥

23. Example 1
Comparison
23
𝑁'∆ℎ = 1.45
own in the figure below
at Point P
𝑁'∆ℎ = 4.3×
4
12
= 1.43

24. Example 1
24
For the seepage problem shown in the figure below
1.Calculate quantity of flow
2.Determine water pressure at Point P

25. Example 2
25

26. Example 2
Geometry, BCs and Mesh
26
-20 -15 -10 -5 0 5 10 15 20
x-coordinate
-10
-5
0
5
y-coordinate
Mesh

27. Example 2
Results
27

28. Example 2
Results
28

29. Example 2
Water pressure
29
𝐹 = 240.3 𝑘𝑁/𝑚
-40 -20 0 20 40 60 80 100 120 140
Pressure (kPa)
-10
-8
-6
-4
-2
0
2
4
6
8
Depth
(m)
Water pressure on sheet pile
upstream
downstream
difference

30. Example 2
Flow nets
30
𝑁'∆ℎ = 8
2.5
23
= 0.869

31. Example 2
Comparison
31
𝑁'∆ℎ = 0.869
𝑁'∆ℎ = 4.5
2.5
12
= 0.938
𝐹 = 158.5 𝑘𝑁/𝑚
𝐹 = 174.1 𝑘𝑁/𝑚

32. Example 3
32

33. Example 3
Geometry, BCs and Mesh
33
-20 -10 0 10 20 30
x-coordinate
-10
-5
0
y-coordinate
Mesh

34. Example 3
Results
34

35. Example 3
Results
35

36. Example 3
Results
36

37. 0 20 40 60 80 100 120
Pressure (kPa)
-8
-6
-4
-2
0
2
4
6
y-coordinate
(m)
Water pressure applied to vertical weir surfaces
Example 3
Water pressure
37
Uplift force applied by water (kN/m) = 482.5 Lateral force applied by water (kN/m) = -120.2
0 5 10 15
x-coordinate (m)
0
20
40
60
80
100
120
Pressure
(kPa)
Water pressure applied to horizontal weir surfaces

38. Example 3
Flow nets
38
Quantity of seepage (m3/m/s)= 1.23
𝑁'∆ℎ = 8
4
26
= 1.23
0.11 0.112 0.114 0.116 0.118 0.12 0.122 0.124
horizontal discharge velocty
-12
-10
-8
-6
-4
-2
0
y-coordinate
Distribution of discharge velocity along vertical line

39. Example 3
Comparison
39
𝑁'∆ℎ = 4.5×
4
15
= 1.20
For the seepage problem shown in the figure below
1.Calculate quantity of flow
2.Determine and plot water pressure distribution on the weir
3.Calculate the uplift force applied to the weir
Unit weight of water = 9.81 kN/m3
Saturated unit weight of soil = 21 kN/m3
Soil permeability = 0.00001 m/s
𝑁'∆ℎ = 1.23
Uplift force = 478.2 𝑘𝑁/𝑚
Uplift force = 482.5 𝑘𝑁/𝑚

40. Example 3
40
For the seepage problem shown in the figure below
1.Calculate quantity of flow
2.Determine and plot water pressure distribution on the weir
3.Calculate the uplift force applied to the weir
Unit weight of water = 9.81 kN/m3
Saturated unit weight of soil = 21 kN/m3
Soil permeability = 0.00001 m/s

41. Anisotropic Permeability
41
𝑘#
𝜕%ℎ
𝜕𝑥%
+ 𝑘$
𝜕%ℎ
𝜕𝑦%
= 0 𝑘# ≠ 𝑘#
𝑘! = 8×10'(𝑚/𝑠 𝑘" = 3×10'(𝑚/𝑠

42. Example Anisotropic
Geometry, BCs and Mesh
42
-60 -40 -20 0 20 40 60 80
x-coordinate
-30
-20
-10
0
y-coordinate
Mesh

43. Example 3 Anisotropic
Results
43

44. Example 3 Anisotropic
Results
44

45. Example Anisotropic
Water pressure
45
Uplift force applied by water (kN/m) = 3342. Lateral force applied by water (kN/m) = -1669.
0 5 10 15 20 25 30 35
x-coordinate (m)
0
50
100
150
200
250
Pressure
(kPa)
Water pressure applied to horizontal weir surfaces
0 50 100 150 200 250
Pressure (kPa)
-10
-5
0
5
10
15
y-coordinate
(m)
Water pressure applied to vertical weir surfaces

46. Example Anisotropic
Flow nets
46
Quantity of seepage (m^3/m/s)= 17.92
-0.1915 -0.191 -0.1905 -0.19 -0.1895 -0.189 -0.1885 -0.188 -0.1875
x-coordinate
-16
-14
-12
-10
-8
-6
-4
-2
vertical
discharge
velocty
Distribution of discharge velocity along horizontal segment within excavation

47. Example Anisotropic/Isotropic
Flow nets
47
Anisotropic: Nf/Nd = 8/18.75
Isotropic: Nf /Nd = 8/38.5

48. Seepage through Layers
48
α1
α2
α1
α2
A
B
C
D
v1AB = v2CD
k1i1AB = k2i2CD
i1 =
hA − hC
AC
=
Δh
AC
i2 =
hB − hD
BD
=
Δh
BD
i1AC = i2BD
k1
AB
AC
= k2
CD
BD
k1
tanα1
=
k2
tanα2

49. Layered Systems
49
k1 = 1
k2 = 0.2
-20
-15
-10
-5
0
5
10
y-coordinate
Mesh

50. Layered Systems
50

51. Layered Systems
51

52. Layered Systems
52
Lateral force (kN/m) =289
-40 -20 0 20 40 60 80 100
Pressure (kPa)
-6
-4
-2
0
2
4
6
Depth
(m)
Water pressure on sheet pile
upstream
downstream
difference

53. Layered Systems
53
Quantity of seepage(m^3/m/s)= 0.54
0 5 10 15 20 25
x-coordinate
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
vertical
discharge
velocty
Distribution of discharge velocity on horizontal line

54. 54
Main Points
1. Cofferdams and weirs are examples of hydraulic
structures.
2. Seepage problems are formulated as boundary value
problems, which are solved with numerical methods
such as finite elements
3. The numerical results are represented using flow nets,
which are made of flow lines and equipotential lines
intersecting at 90 degrees and forming curvilinear
squares (isotropic & homogenous cases)
4. Flow nets are convenient to use for isotropic
permeability but more challenging for anisotropic
permeability and layered systems.

55. 55
Main Points
5. Flow nets, which used to be sketched by hand,
are now obtained by computations.
6. Flow nets are used to
• Quantity of seepage and hydraulic gradient
• Pressure distribution and resulting forces
7. The quantity of flow is q = k Nf Δh where
• k = permeability
• Nf = number of flow channels
• Δh = total head increment between to
potential lines
8. In most cases, Δh = Total head drop/Nd where
Nd = number of equipotential intervals