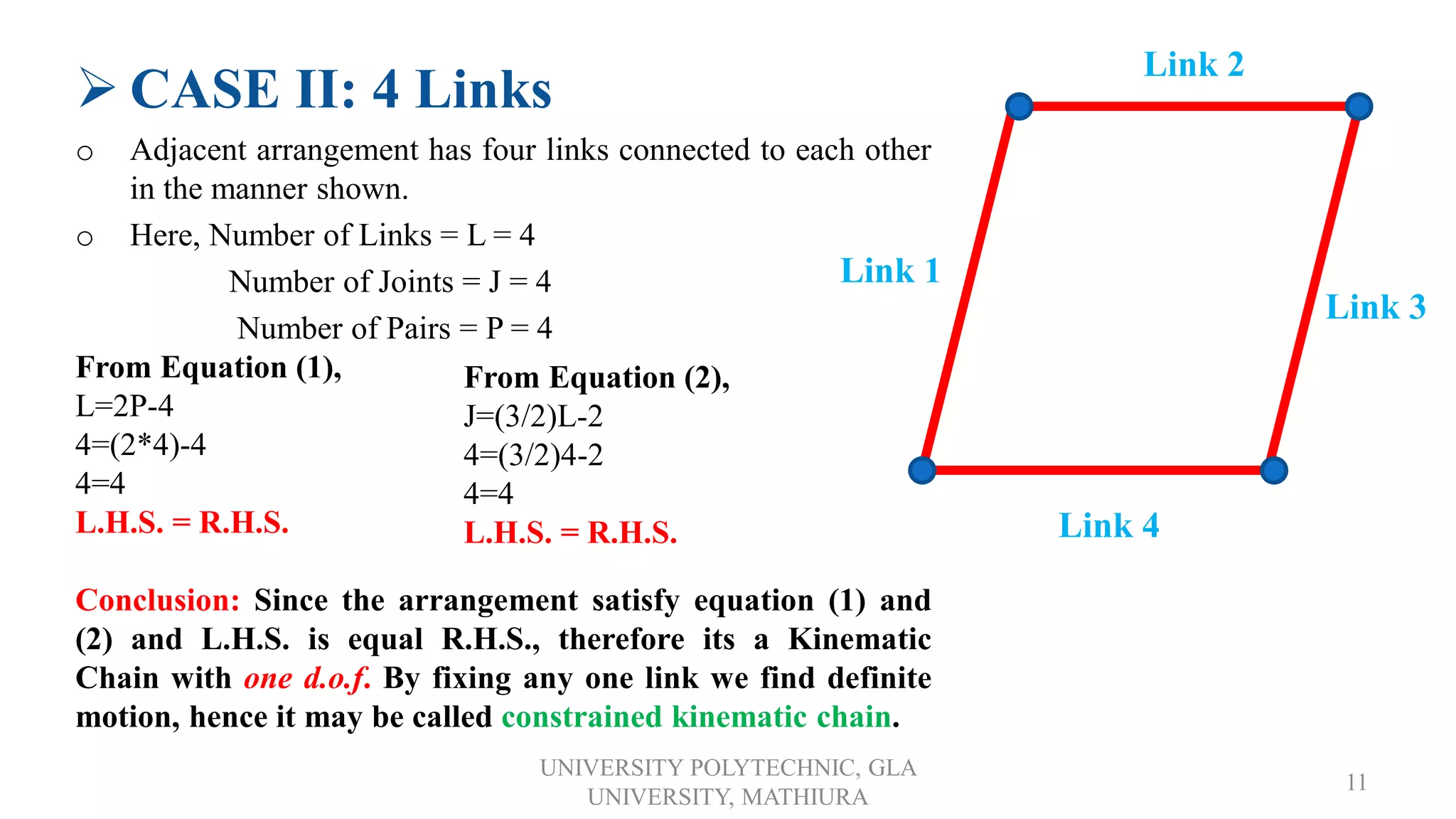
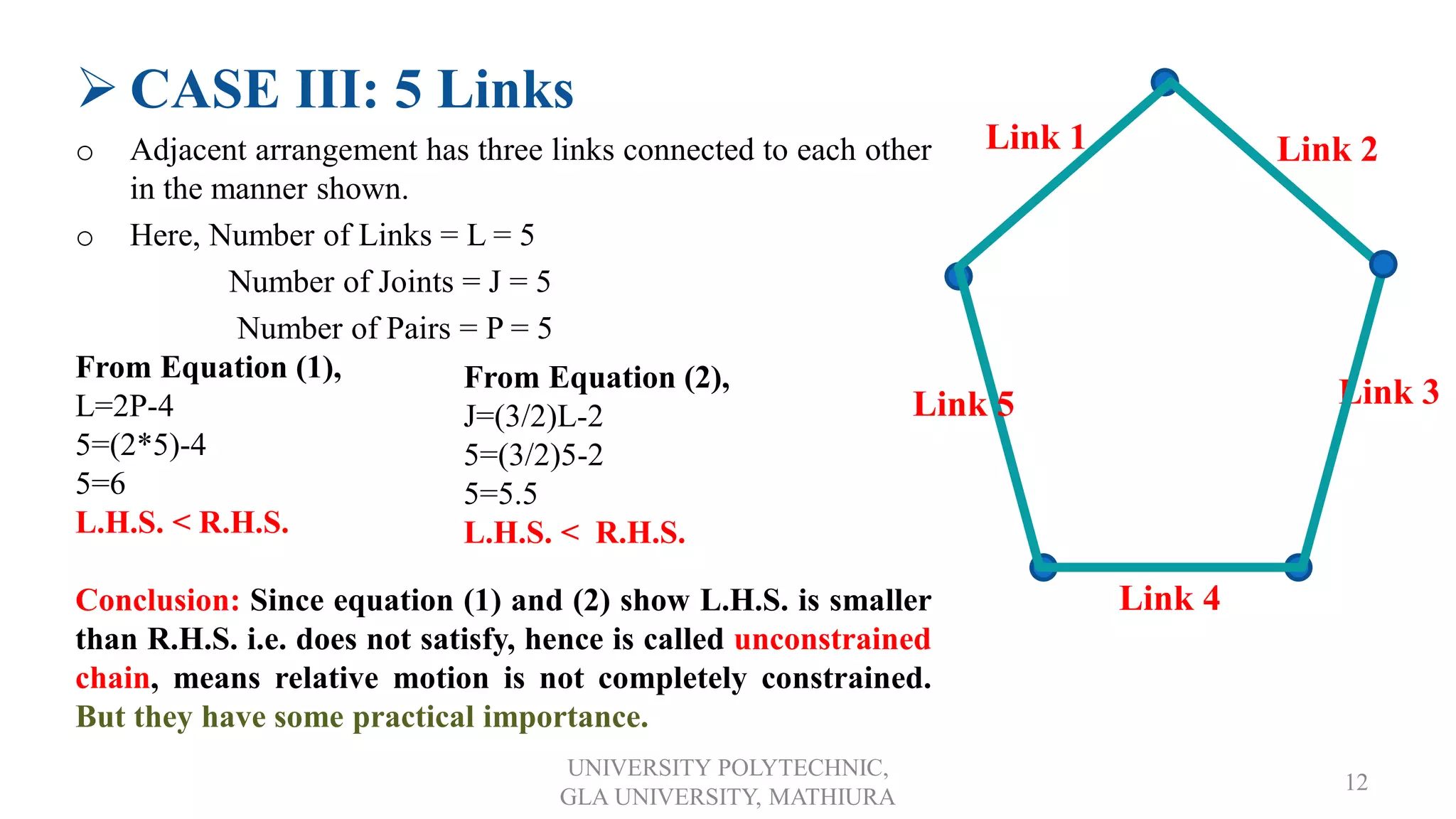
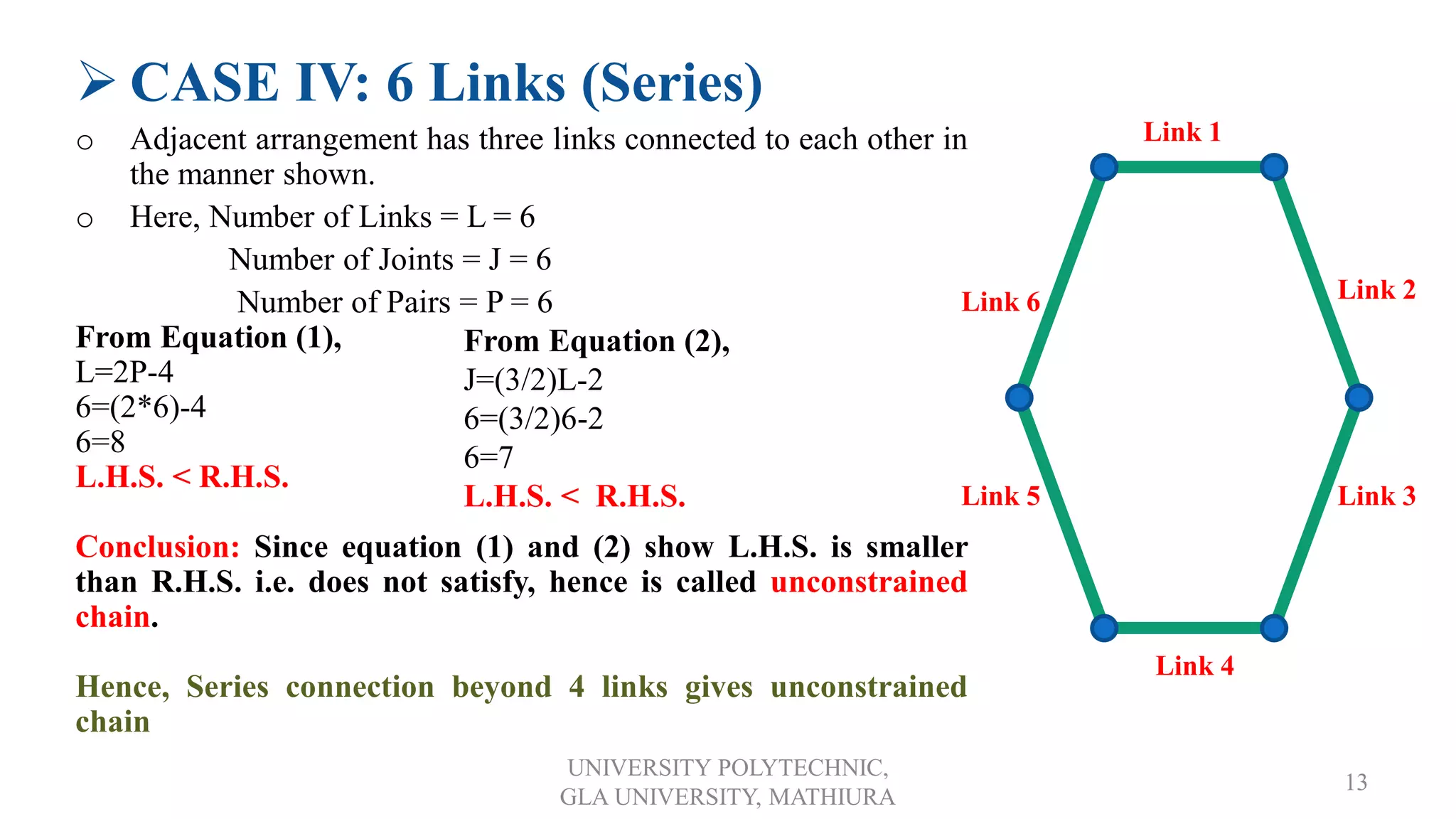
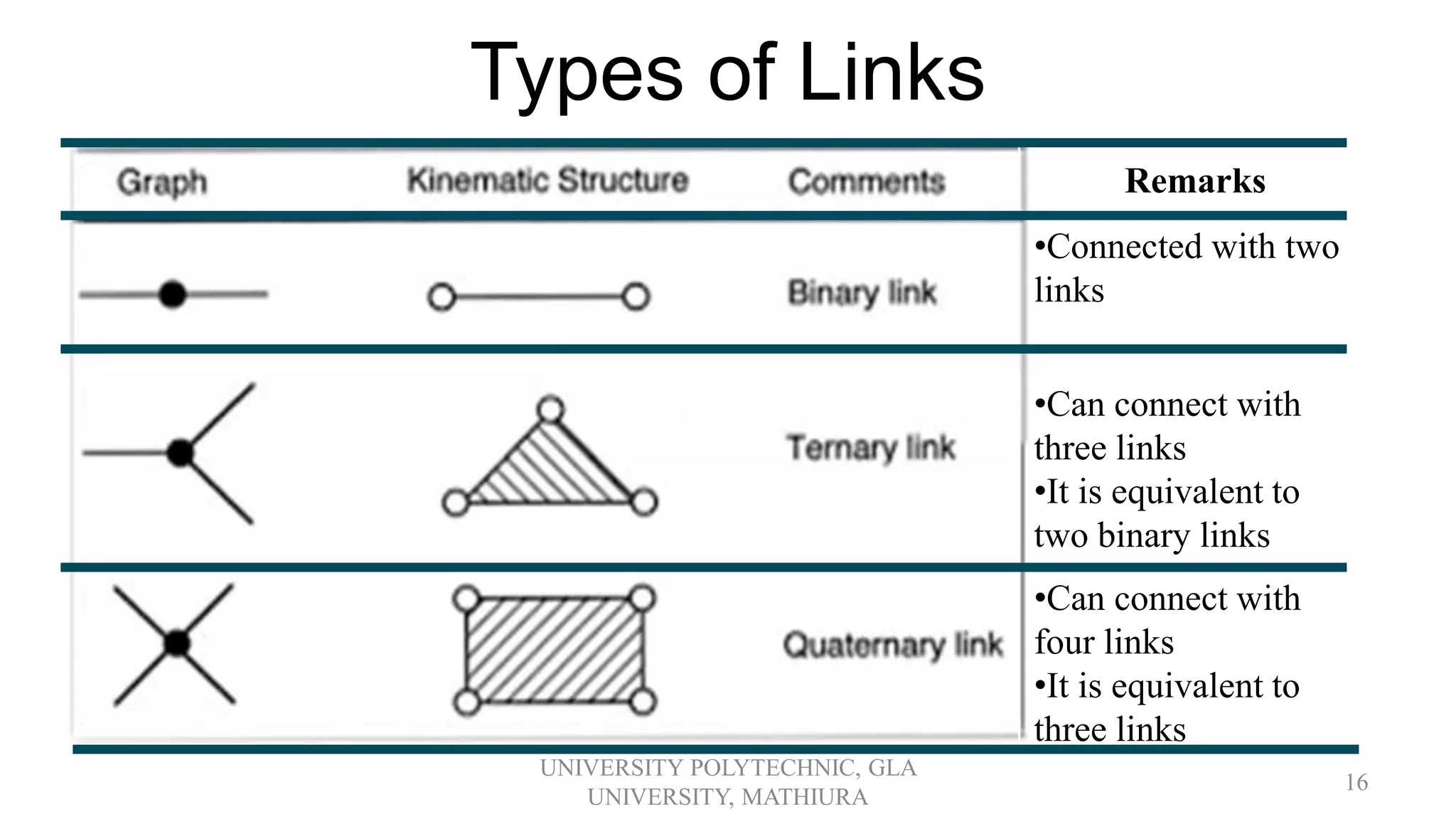
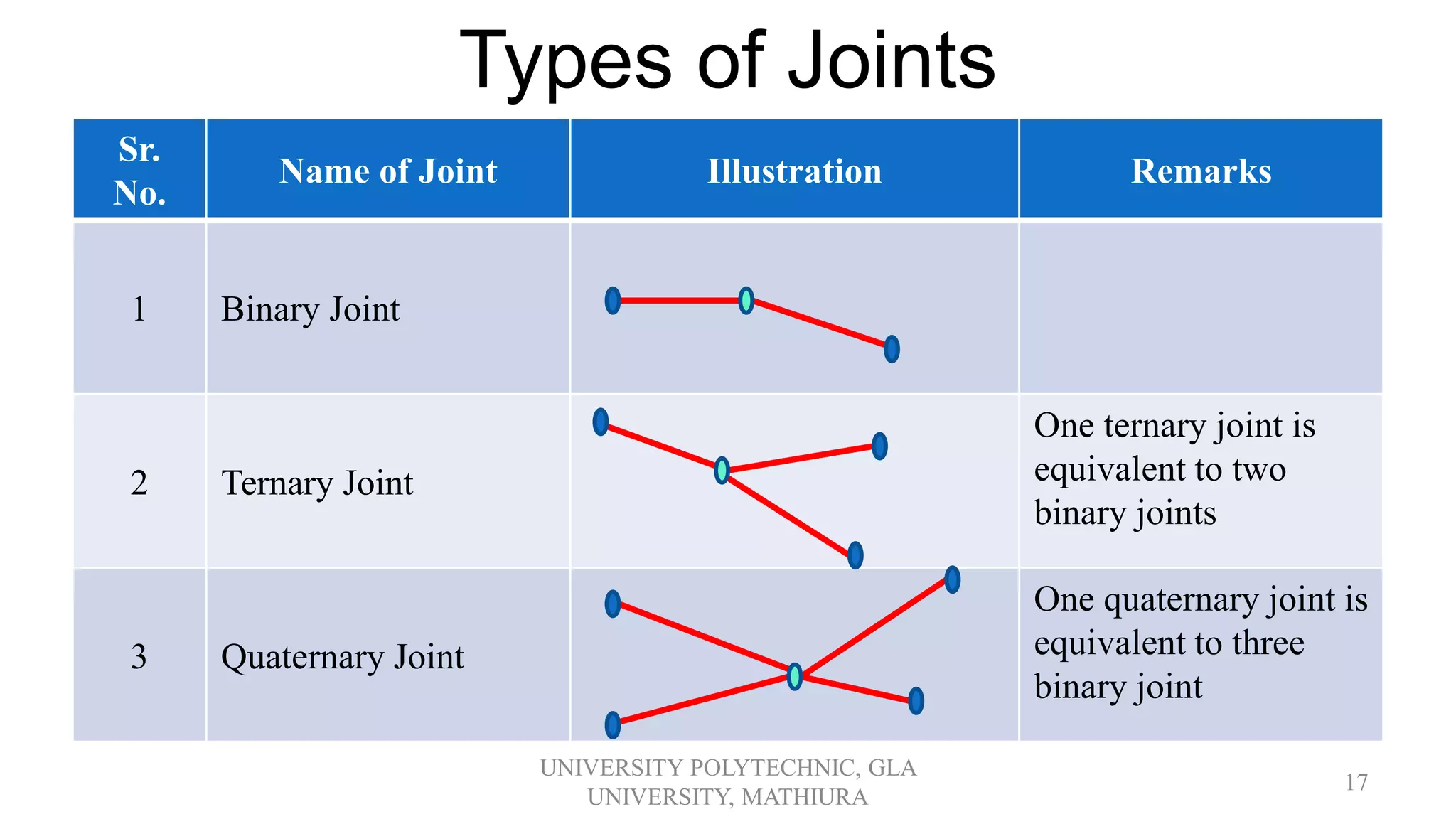
This document provides an overview of kinematic chains and concepts related to their motion analysis including: 1. It defines constrained motion and classifies it as completely, incompletely, and successfully constrained. 2. It introduces kinematic chains, distinguishing between open and closed chains. Formulas are provided to analyze chains using the number of links, joints, and pairs. 3. Common criteria for analyzing kinematic chains are described, including Kutzbach's criterion for determining degrees of freedom and Grubler's criterion for minimum links required for single degree of freedom chains.

1. THEORY OF MACHINES
(DME 5201)
UNIVERSITY POLYTECHNIC
GLA UNIVERSITY,
MATHURA
LECTURE 3-4

2. MODULE -1_Lecture 3- 4 : Contents
UNIVERSITY POLYTECHNIC
GLA UNIVERSITY, MATHIURA
2
• Constrained Motion
• Types of joints (otb connectivity)
• Kinematic chain and conditions
• Kutzback criteria
• Grubler’s criteria
• Degree of freedom

3. Constrained Motion
• Constrained motion results when an object is forced to move
in a restricted way.
– For example a fan rotates on its axis, it is not allowed to translate
– Wheel of car is made to rotate only
– Piston is made to slide inside cylinder
• Constrained motion can be classified as-
1. Completely constrained motion
2. Incompletely constrained motion
3. Successfully constrained motion
UNIVERSITY POLYTECHNIC,
GLA UNIVERSITY, MATHIURA
3

4. 1. Completely Constrained Motion
 When the motion between a pair is limited to
a definite direction irrespective of the
direction of force applied, then the motion is
said to be a completely constrained motion.
• Example-
1. The triangular bar can translate only
2. The round bar can rotate only and translation is
restricted by using collars
UNIVERSITY POLYTECHNIC,
GLA UNIVERSITY, MATHIURA
4

5. 2. Incompletely Constrained Motion
 When the motion between a pair can take
place in more than one direction, then the
motion is called an incompletely constrained
motion.
• Example-
1. The round bar can rotate as well as translate
inside round hole
UNIVERSITY POLYTECHNIC,
GLA UNIVERSITY, MATHIURA
5

6. 3. Successfully Constrained Motion
 A kinematic pair is said to be partially or
successfully constrained if the relative motion
between its links occurs in a definite direction,
not by itself, but by some other means.
Example-
1. Footstep bearing
2. Piston
UNIVERSITY POLYTECHNIC,
GLA UNIVERSITY, MATHIURA
6

7. Kinematic Chain
UNIVERSITY POLYTECHNIC,
GLA UNIVERSITY, MATHIURA
7

8.  In mechanical engineering, a kinematic
chain is an assembly of rigid bodies
connected by joints to provide constrained
(or desired) motion.
Kinematic chains can be classified as:
• Open Kinematic Chain: There are bodies in the chain
with only one associated kinematic joint
• Closed Kinematic Chain: Each body in the chain has at
least two associated kinematic joints
 The above concept is enough to study some
criterions and nature of kinematic chains.
 K’Chains will be continued in lecture 5 and
onwards.
UNIVERSITY POLYTECHNIC,
GLA UNIVERSITY, MATHIURA
8

9. Finding out Nature of Kinematic Chain
Consider,
L= Number of links
J= Number of Joints
P= Number of Pairs
 If each link is assumed to form two pairs with two adjacent links, then ,
L=2P- 4 …...……………..(1)
 Relationship between number of links and joints can be given as,
J= (3/2)L - 2 ………………(2)
 Now these two equations (1) and (2) will be applied to find our nature
of kinematic chains.
UNIVERSITY POLYTECHNIC,
GLA UNIVERSITY, MATHIURA
9

10.  CASE I: 3 Links
o Adjacent arrangement has three links connected to each other
in the manner shown.
o Here, Number of Links = L = 3
Number of Joints = J = 3
Number of Pairs = P = 3
From Equation (1),
L=2P-4
3=(2*3)-4
3=2
L.H.S. > R.H.S.
Conclusion: Since the arrangement does not satisfy equation
(1) and (2) and L.H.S. is greater than R.H.S. therefore its not
a Kinematic Chain and hence no relative motion is possible.
These chains are called Locked Chains and form structure.
UNIVERSITY POLYTECHNIC,
GLA UNIVERSITY, MATHIURA
10
Link 1
Link 3
Link 2
From Equation (2),
J=(3/2)L-2
3=(3/2)3-2
3=2.5
L.H.S. > R.H.S.

11. UNIVERSITY POLYTECHNIC, GLA
UNIVERSITY, MATHIURA
11
 CASE II: 4 Links
o Adjacent arrangement has four links connected to each other
in the manner shown.
o Here, Number of Links = L = 4
Number of Joints = J = 4
Number of Pairs = P = 4
From Equation (1),
L=2P-4
4=(2*4)-4
4=4
L.H.S. = R.H.S.
Conclusion: Since the arrangement satisfy equation (1) and
(2) and L.H.S. is equal R.H.S., therefore its a Kinematic
Chain with one d.o.f. By fixing any one link we find definite
motion, hence it may be called constrained kinematic chain.
Link 1
Link 3
Link 4
Link 2
From Equation (2),
J=(3/2)L-2
4=(3/2)4-2
4=4
L.H.S. = R.H.S.

12. UNIVERSITY POLYTECHNIC,
GLA UNIVERSITY, MATHIURA
12
 CASE III: 5 Links
o Adjacent arrangement has three links connected to each other
in the manner shown.
o Here, Number of Links = L = 5
Number of Joints = J = 5
Number of Pairs = P = 5
From Equation (1),
L=2P-4
5=(2*5)-4
5=6
L.H.S. < R.H.S.
Conclusion: Since equation (1) and (2) show L.H.S. is smaller
than R.H.S. i.e. does not satisfy, hence is called unconstrained
chain, means relative motion is not completely constrained.
But they have some practical importance.
Link 1
Link 3
Link 4
Link 2
From Equation (2),
J=(3/2)L-2
5=(3/2)5-2
5=5.5
L.H.S. < R.H.S.
Link 5

13. UNIVERSITY POLYTECHNIC,
GLA UNIVERSITY, MATHIURA
13
 CASE IV: 6 Links (Series)
o Adjacent arrangement has three links connected to each other in
the manner shown.
o Here, Number of Links = L = 6
Number of Joints = J = 6
Number of Pairs = P = 6
From Equation (1),
L=2P-4
6=(2*6)-4
6=8
L.H.S. < R.H.S.
Conclusion: Since equation (1) and (2) show L.H.S. is smaller
than R.H.S. i.e. does not satisfy, hence is called unconstrained
chain.
Hence, Series connection beyond 4 links gives unconstrained
chain
Link 1
Link 3Link 5
Link 2
From Equation (2),
J=(3/2)L-2
6=(3/2)6-2
6=7
L.H.S. < R.H.S.
Link 4
Link 6

14. UNIVERSITY POLYTECHNIC,
GLA UNIVERSITY, MATHIURA
14
 CASE V: 6 Links
o Adjacent arrangement has three links connected to each other
in the manner shown.
o Here, Number of Links = L = 6
Number of Joints = J = 7
Number of Pairs = P = 5
From Equation (1),
L=2P-4
6=(2*5)-4
6=6
L.H.S. = R.H.S.
Conclusion: Since equation (1) and (2) are satisfied, hence it is
a kinematic chain.
From Equation (2),
J=(3/2)L-2
7=(3/2)6-2
7=7
L.H.S. = R.H.S.
1 3
6
5
2
4
NOTE- The chain having more than four links are known as Compound K’Chain.

15. TYPES OF LINKS AND JOINTS
(On the basis of connectivity)
UNIVERSITY POLYTECHNIC, GLA
UNIVERSITY, MATHIURA
15

16. Types of Links
UNIVERSITY POLYTECHNIC, GLA
UNIVERSITY, MATHIURA
16
Remarks
•Connected with two
links
•Can connect with
three links
•It is equivalent to
two binary links
•Can connect with
four links
•It is equivalent to
three links

17. Types of Joints
Sr.
No.
Name of Joint Illustration Remarks
1 Binary Joint
2 Ternary Joint
One ternary joint is
equivalent to two
binary joints
3 Quaternary Joint
One quaternary joint is
equivalent to three
binary joint
UNIVERSITY POLYTECHNIC, GLA
UNIVERSITY, MATHIURA
17

18. UNIVERSITY POLYTECHNIC, GLA
UNIVERSITY, MATHIURA
18
If there are n number of
links connected at one
junction, then at that
junction,
No. of Binary Joints = n-1

19. Klein’s Equation
• To determine the nature of chain following equation is used, which was
given by A.W. Klein,
Where, j = number of binary joints
h = number of higher pairs
L= number of links
 If L.H.S = R.H.S, kinematic or constrained chain
 If L.H.S > R.H.S, chain is locked chain
UNIVERSITY POLYTECHNIC, GLA
UNIVERSITY, MATHIURA
19

20. Number of Degree of Freedom and Kutzbach Criterion
• Degree of freedom can be defined as how many possible moves
can a mechanism or kinematic chain may have.
• If a mechanism has L number of links, J is number of binary joints
or lower pairs and h is number of higher pairs, then according to
Kutzbach criterion, d.o.f. can be given by for plane mechanisms-
n= 3 (L-1) – 2 J - h
UNIVERSITY POLYTECHNIC, GLA
UNIVERSITY, MATHIURA
20

21. Grubler’s Criteria
• It is derived from Kutzbach criteria where d.o.f. is taken as one and total higher pairs as
zero.
From Kutzbach criteria, n= 3 (L-1) – 2 J – h
Putting n=1,
1= 3 ( L-1) – 2 J
Case1: For, L=1, J=0  LHS > RHS
Case 2: For, L=2, J=1 LHS = RHS
Case 3: For, L=3, J=3  LHS > RHS
Case 4: For, L=4, J=4  LHS = RHS
 Simplest possible mechanism is possible with least four links.
 Single d.o.f. is not possible for mechanisms having odd number of links.
UNIVERSITY POLYTECHNIC, GLA
UNIVERSITY, MATHIURA
21

22. Grashoff’s Law
• The Grashof's law states that for a four-bar linkage system, the sum of the
shortest and longest link of a planar quadrilateral linkage is less than or
equal to the sum of the remaining two links, then the shortest link can
rotate fully with respect to a neighboring
UNIVERSITY POLYTECHNIC, GLA
UNIVERSITY, MATHIURA
22