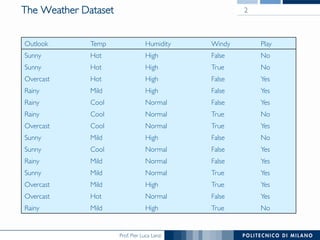
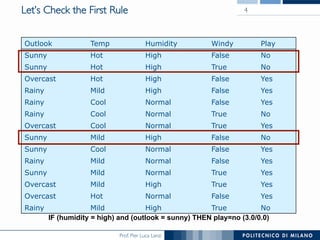
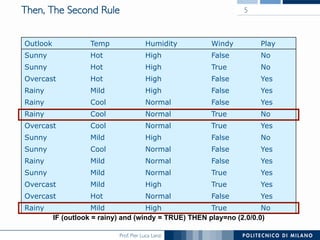
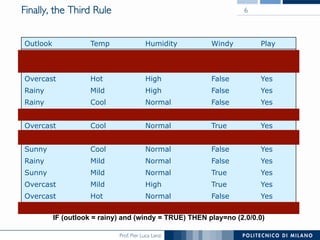
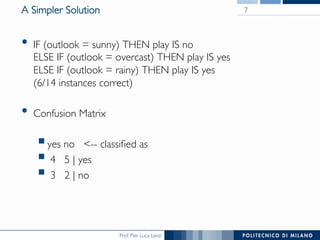
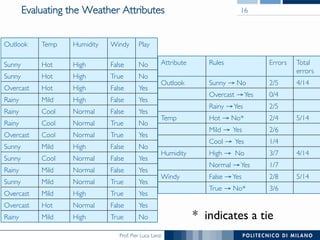
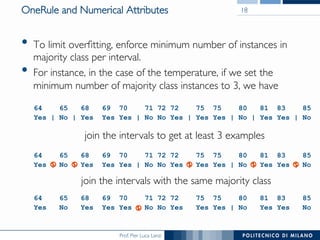
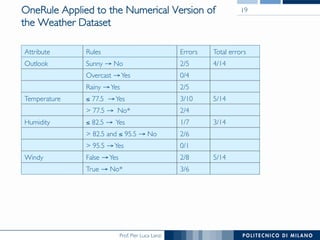
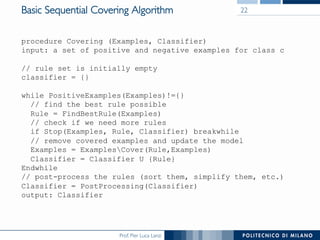
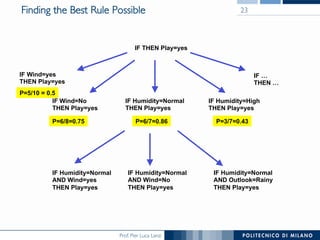
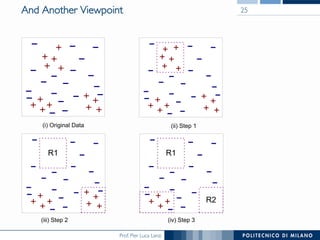
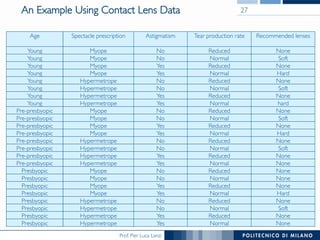
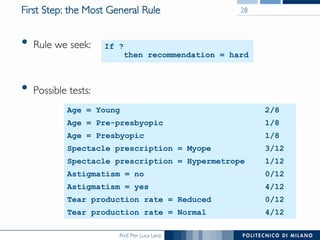
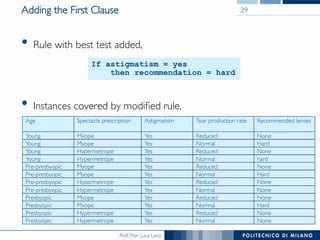
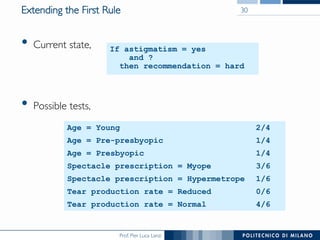
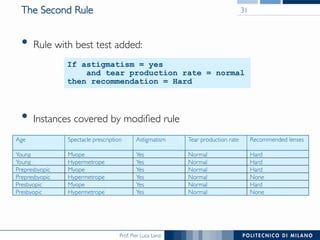
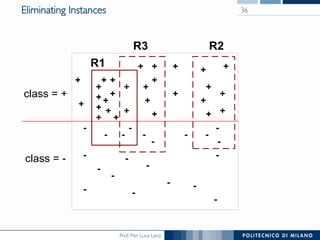
The document discusses rule induction in data and text mining, focusing on classification rules and their development from datasets like weather data. It presents several examples of classification rules based on conditions such as humidity and outlook, and details methodologies like sequential covering and one-rule learning for rule creation. The document also addresses concepts such as rule accuracy, conflict resolution, and handling numeric attributes while forming these rules.