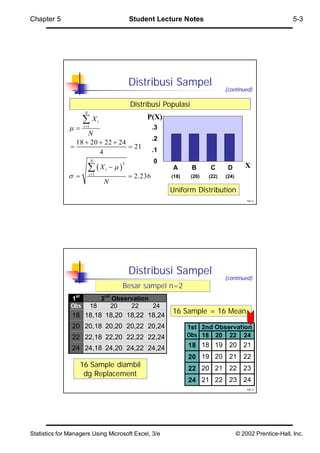
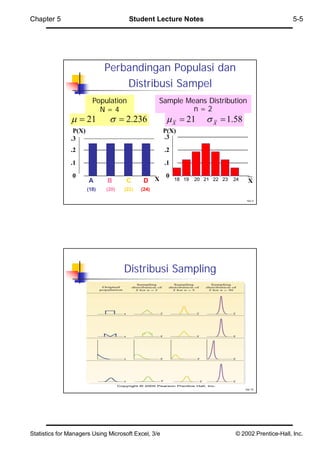
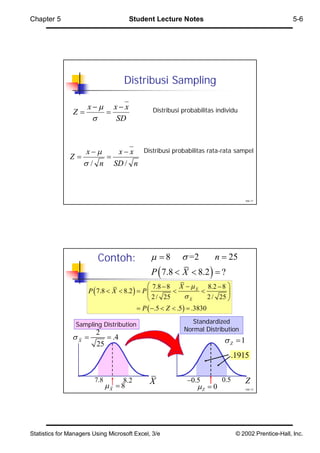
Bab 5 membahas distribusi sampel dan distribusi probabilitas individu dan proporsi sampel. Distribusi sampel adalah distribusi dari rata-rata atau proporsi yang diambil berulang kali dari populasi. Distribusi sampel cenderung mendekati distribusi normal berdasarkan teorema batas pusat meskipun distribusi populasi tidak normal. Rata-rata distribusi sampel sama dengan rata-rata populasi dan variansinya berkurang sebanding dengan ukuran sampel. Bab ini juga menj