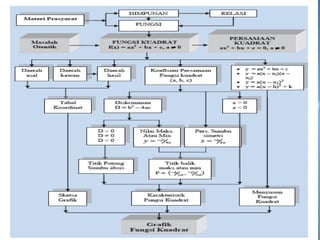
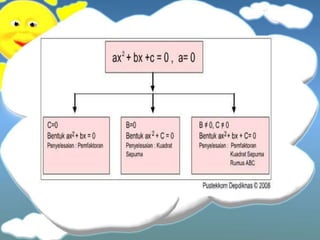
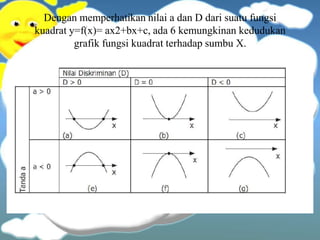
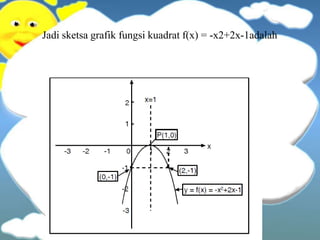
This document discusses quadratic equations and functions. It explains how to solve quadratic equations by factoring, completing the square, and using the quadratic formula. It also discusses using the discriminant to determine the number and type of roots. Properties of quadratic functions such as the sum and product of roots are covered. Methods for constructing quadratic equations and functions given certain properties are provided. Finally, it briefly discusses sketching the graph of a quadratic function.

1. KELAS IX GENAP
TAHUN PELAJARAN
2021/2022

4. 1. Menyelesaikan Persamaan
kuadrat
Persamaan kuadrat dapat diselesaikan dengan beberapa cara, yaitu
dengan:
a) memfaktorkan,
b) melengkapkan kuadrat sempurna,
c) menggunakan rumus.

6. ax2 + bx + c = 0 dapat dinyatakan menjadi a (x – x1) (x – x2)
= 0.
Nilai x1 dan x2 disebut akar-akar (penyelesaian) persamaan
kuadrat.
Contoh 1 :
Selesaikan x2 – 4 x + 3 = 0
Jawab: x2 – 4 x + 3 = 0
(x – 3) (x – 1) = 0
x – 3 = 0 atau x – 1 = 0
x = 3 atau x = 1
Jadi, penyelesaian dari x2 – 4 x + 3 = 0 adalah 3 dan 1.

8. c) Menggunakan rumus abc
Selain menggunakan cara pemfaktoran, untuk
menentukanakar-akarpersamaan kuadrat 𝑎𝑥2 + 𝑏𝑥 + 𝑐 =
0 adalah dengan menggunakan rumus kuadrat atau sering
disebut rumus abc. Rumus kuadrat dapat diturunkan dengan
cara melengkapkan kuadrat sempurna sebagai berikut:
𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0
• Kedua ruas ditambah –c, maka menjadi:
𝑎𝑥2 + 𝑏𝑥 = −𝑐

9. Kedua ruas dibagi dengan a dimana a
+ =
𝑎𝑥2 𝑏𝑥 −𝑐
𝑎 𝑎 𝑎
↔ 𝑥2 +
𝑏𝑥
=
−𝑐
𝑎 𝑎
Lengkapkan kuadrat pada ruas kiri, dengan
cara menambah
𝑏 2
pada kedua ruas,
2𝑎
maka di peroleh :
𝑏𝑥
𝑎
𝑥2 + +
𝑏
2𝑎
2
=
−𝑐
𝑎
+
𝑏
2𝑎
2
Nyatakan ruas kiri dalam bentuk kuadrat
sempurna yaitu :
𝑥 +
𝑏
2𝑎
2
𝑐
= − +
𝑏2
𝑎 4𝑎2
𝑏
𝑥 +
2𝑎
2
4𝑎𝑐 𝑏2
= − +
4𝑎2 4𝑎2
𝑏
𝑥 +
2𝑎
2
=
𝑏2 − 4𝑎𝑐
𝑥 + = ±
4𝑎2
𝑏2 − 4𝑎𝑐
𝑥 +
𝑏
2𝑎
𝑏
2𝑎
= ±
4𝑎2
𝑏2 − 4𝑎𝑐
4𝑎2
𝑏2 − 4𝑎𝑐
𝑏
𝑥 + = ±
2𝑎
𝑏
𝑥 = − ±
2𝑎
𝑏2 − 4𝑎𝑐
𝑥 =
2𝑎 2𝑎
−𝑏 ± 𝑏2 − 4𝑎𝑐
2𝑎
𝑥1,2 =
Jadi rumus akar-akar persamaan kuadrat
ax2+ bx+ c =0
−𝑏 ± 𝑏2 − 4𝑎𝑐
2𝑎

10. Contohsoal:
Tentukan akar-akar persamaan kuadrat
dengan cara menggunakan rumus
kuadrat 6𝑥2– 5x + 1 = 0
Jawab :
a=6 , b=-5, c=1
𝑥1,2 =
−𝑏 ± 𝑏2 − 4𝑎𝑐
𝑥1,2 =
−(−5) ±
2𝑎
(−5)2−4.6.1
𝑥1,2 =
2.6
5 ± 25 − 24
𝑥1,2 =
12
5 ± 1
𝑥1,2 =
12
5 ± 1
12
Jadi :
𝑥1 =
5 + 1 6 1
12
=
12
=
2
Atau 𝑥2 = 5−1
= 4
= 1
12 12 3
Hp =
1
, 1
2 3

11. Penggunaan Diskriminan
𝑥1,2 =
Dalam kegiatan 1 bagian b, Anda telah mempelajari cara menentukan akar-akar
persamaan kuadrat ax2 +bx + c = 0 (a) dengan menggunakan rumus kuadrat atau
rumus abc, yaitu:
−𝑏 ± 𝑏2 − 4𝑎𝑐
2𝑎
Dari rumus itu tampak bahwa akar-akar persamaan kuadrat sangat ditentukan
oleh nilai 𝑏2– 4ac.
Bentuk 𝑏2– 4ac disebut diskriminan (pembeda) dari persamaan kuadrat a𝑥2+ bx
+ c= 0 dan dilambangkan dengan huruf D, sehingga D = 𝑏2– 4ac.
Pemberian nama/istilah diskriminan D = 𝑏2– 4ac , dikarenakan nilai D = 𝑏2-4ac
ini yang mendiskriminasikan (membedakan) jenis akar-akar persamaan
kuadrat.Jadi kegunaan diskriminan adalah untuk menentukan jenis akar-akar
persamaan kuadrat

12. Jenis-jenis Akar Persamaan
Kuadrat
• D > 0 maka ÖD merupakan bilangan real positif, sehingga
persamaan kuadrat mempunyai dua akar real berlainan, .
• D = 0 maka ÖD = 0, sehingga persamaan kuadrat mempunyai dua
akar real sama. .
• D < 0 maka ÖD merupakan bilangan tidak real (imajiner), maka
persamaan kuadrat tidak mempunyai akar real atau persamaan kuadrat
mempunyai akar tidak real.

13. • Tanpa menyelesaikan persamaan lebih dahulu, tentukan jenis-jenis
akar persamaan kuadrat x2 + 5 x + 2 = 0
Jawab :x2 + 5 x + 2 = 0
• a = 1 , b = 5 , c = 2
D = b2 – 4ac = 52 – 4 . 1 . 2 = 25 – 8 = 17
Ternyata D > 0. Jadi, persamaan x2 + 5 x + 2 = 0 mempunyai dua akar
real berlainan

14. Jumlahdan hasilkali akar-akar persamaan
kuadrat
Persamaan kuadrat ax2+ bx+ c = 0 mempunyai akar x1dan x2 , dari rumus
𝑥1 dan 𝑥2
= −𝑏+ 𝑏2−4𝑎𝑐
= −𝑏− 𝑏2−4𝑎𝑐
2𝑎 2𝑎
Dapat ditentukan :
𝑥1 + 𝑥2 =
a. Jumlah akar-akar persamaan kuadrat
−𝑏 + 𝑏2 − 4𝑎𝑐
2𝑎
+
−𝑏 − 𝑏2 − 4𝑎𝑐
𝑥1 + 𝑥2 =
2𝑎
−𝑏 + 𝑏2 − 4𝑎𝑐 − 𝑏 − 𝑏2 − 4𝑎𝑐
𝑥1 + 𝑥2 =
2𝑎
−2𝑏
𝑥1 + 𝑥2 =
2𝑎
−𝑏
𝑎

15. b) Hasil kali akar-akar persamaan kuadrat.
𝑥1. 𝑥2 =
𝑥1. 𝑥2 =
−𝑏 + 𝑏2 − 4𝑎𝑐 −𝑏 − 𝑏2 − 4𝑎𝑐
2𝑎 2𝑎
−𝑏 2 + 𝑏 𝑏2 − 4𝑎𝑐 − 𝑏 𝑏2 − 4𝑎𝑐 − 𝑏2 − 4𝑎𝑐
4𝑎2
𝑥1. 𝑥2 =
𝑏2 − 𝑏2 + 4𝑎𝑐
4𝑎2
4𝑎𝑐
𝑥1. 𝑥2 =
4𝑎2
𝑐
𝑥1. 𝑥2 =
𝑎

16. CONTOH
Akar-akar x2 – 3x + 4 = 0 adalah x1 dan x2. Dengan tanpa menyelesaikan
persamaan tersebut, hitunglah nilai x1
2 + x2
2
Jawab :
𝑥1 + 𝑥2 =
𝑎
−𝑏 −(−3)
1
= = 3
𝑐 4
𝑥1. 𝑥2 =
𝑎
=
1
= 4
x1
2 + x2
2 = x1
2 + x2
2 + 2 x1.x2 – 2 x1.x2
= (x1 + x2)2 – 2 x1x2 = 2(3)2– 2 . 4 =9-8= 1

17. Menyusun Persamaan Kuadrat
a) Menyusun persamaan kuadrat dengan menggunakan
perkalian faktor
Pada bahasan terdahulu, persamaan kuadrat x2 + p x + q = 0
dapat dinyatakan sebagai (x – x1) (x – x2) = 0 sehingga
diperoleh akar-akar persamaan itu x1 dan x2. Dengan
demikian jika akar-akar persamaan kuadrat x1 dan x2 maka
persamaannya adalah (x – x1) (x – x2) = 0.

18. Contoh
• Tentukan persamaan kuadrat yang akar-
akarnya 3 dan -2.
Jawab: (x – x1) (x – x2) = 0
(x – 3) (x – (-2)) = 0
(x – 3) (x + 2) = 0
x2 – 3 x + 2 x – 6 = 0
x2 – x – 6 = 0.

19. Menyusun persamaan kuadrat menggunakan jumlah dan
hasil kali akar-akar
1 2 𝑎
Dengan menggunakan x + x = −𝑏
dan
1 2 𝑎
𝑥 . 𝑥 = 𝑐
, maka akan diperoleh persamaan:
• x2– (x1 + x2)x + x1x2 = 0.

20. Contoh
• Susunlah persamaan kuadrat baru yang akarnya 2 kali akar persamaan
2x2 – 3x + 1 = 0.
Jawab:
• Misalkan akar-akar persamaan 2x2 – 3x + 1 = 0 adalah x1 dan x2 serta
persamaan kuadrat baru adalah a dan b, maka a = 2x1 dan b = 2x2
a + b = 2(x1 + x2) = 2
a b = 2x1 . 2x2 = 4x1 x2 = 4 . = 2
Persamaan kuadrat yang akarnya a dan b adalah:
x2 – (a + b)x + ab = 0.
Persamaan kuadrat baru adalah x2 – 3x + 2 = 0..

21. Menyusun persamaan kuadrat yang akar-
akarnya berkaitan dengan akar-akar persamaan
kuadrat lain
Seringkali kita mendapatkan suatu persamaan kuadrat yang akar-akarnya
berhubungan dengan akar-akar persamaan yang lain.
Contoh 1:
Susunlah persamaan kuadrat baru yang akar-akarnya 3 lebih dari akar-akar
persamaan x2 – 2x + 3 = 0.
Jawab:
Misal akar-akar persamaan x2 – 2x + 3 = 0 adalah x1 dan x2. ® x1 + x2 = 2 , x1 x2
= 3.
Jika akar-akar persamaan kuadrat baru adalah p dan q, maka p = x1 + 3 dan q
= x2 +3
p + q = (x1 + 3) + (x2 + 3)
= x1 + x2 + 6
= 2 + 6 = 8
p q = (x1 + 3) (x2 + 3)
= x1 x2 + 3(x1 + x2) + 9
= 3 + 2(2) = 9 = 18
Persamaan kuadrat yang akar-akarnya p dan q adalah x2 – (p + q) + pq = 0.
Persamaan kuadrat baru adalah x2 – 8x + 18 = 0.

22. Fungsi Kuadrat
Ingat !
• Fungsi atau Pemetaan adalah relasi himpunan A ke himpunan B yang
memasangkan setiap anggota himpunan A dengan tepat satu anggota
pada himpunan B.
• Apabila fungsi itu diberi nama f, maka fungsi tersebut dituliskan
dengan lambang f:A→B (dibaca: f memetakan Ake B).

23. Pengertian
Fungsi f pada R yang ditentukan oleh: f(x) = ax2 + bx + c dengan a, b,
dan c bilangan real dan disebut fungsi kuadrat.
Jika f(x) = 0 maka diperoleh persamaan kuadrat ax2 + bx + c = 0. Nilai-
nilai x yang memenuhi persamaan itu disebut nilai pembuat nol fungsi f.
Nilai fungsi f untuk x = p ditulis f(p) = ap2 + bp + c.
• Contoh 1:
Ditentukan: f(x) = x2 – 6x – 7
Ditanyakan:
1. nilai pembuat nol fungsi f
2. nilai f untuk x = 0 , x = –2

24. Lanjutan
• Jawab:
Nilai pembuat nol fungsi f diperoleh jika f(x) = 0
x2 – 6 x – 7 = 0
(x – 7) (x + 1) = 0
x = 7 atau x = –1
Jadi pembuat nol fungsi f adalah 7 dan –1
Untuk x = 0 maka f(0) = –7
x = –2 maka f(–2) = (–2)2 – 6 (–2) – 7 = 9

25. Gambar grafik fungsi kuadrat
Misalkan suatu fungsi kuadrat ditentukan dengan persamaan
f(x)= ax2 +bx +c (a ≠ 0), a, b, c, R. Grafik fungsi kuadrat itu
adalah sebuah parabola dengan persamaan y = ax2 + bx + c.
Untuk menggambar sketsa grafik fungsi kuadrat secara
umum, dapat digunakan langkah-langkah sebagai berikut:
(i). titik potong grafik dengan sumbu x dan sumbu y.
(ii) titik balik atau titik puncak parabola.
(iii) Persamaan sumbu simetri.

26. Langkah-langkah
Titik potong Grafik dengan Sumbu X dan Sumbu y
a) Titik Potong Grafik dengan Sumbu X
• Titik potong grafik dengan sumbu X diperoleh jika y= 0, sehingga ax2+bx + c
= 0 merupakan kuadrat dalam x.
Akar-akar persamaan kuadrat itu merupakan absis titik-titik potongnya
dengan sumbu x. nilai diskriminan persamaan kuadrat ax2+bx+c= 0, yaitu
D = b2- 4ac menentukan banyak titik potong grafik dengan sumbu x.
1. jika D>0, maka grafik fungsi f memotong sumbu x di dua titik yang
berlainan.
2.Jika D=0, maka grafik fungsi f memotong sumbu X di dua titik yang
berimpit. Dalam hal ini, grafik fungsi f dikatakan menyinggung sumbu X.
3. Jika D<0, maka grafik fungsi f tidak memotong maupun menyinggung
sumbu x.

27. Titik Potong Grafik dengan sumbu y
Titik potong grafik dengan sumbu y diperoleh jika x = 0,
sehingga
y = 𝑎(0)2+ b(0) + c = c- Jadi, titik potong grafik dengan
sumbu y adalah (0,c)
titik balik atau titik puncak dan Persamaan sumbu
simetri
cara 1 :
Mencari nilai xp menggunakan 𝑥𝑝 = −𝑏
2𝑎
2𝑎
Untuk mencari 𝑦 , substitusikan nilai 𝑥 = −𝑏
ke 𝑦 =
𝑝 𝑝
𝑓 𝑥 =𝑎𝑥2 + 𝑏𝑥 + 𝑐

28. • Cara 2 : menggunakan rumus untuk menentukan titik
𝑥𝑝, 𝑦𝑝 = 𝑝 𝑝
atau 𝑥 , 𝑦 =
2
−𝑏
, 𝑏 −4𝑎𝑐 −𝑏
, 𝐷
2𝑎 −4𝑎 2𝑎 −4𝑎
• Cara 3 : menggunakan turunan (titik puncak = titik
stationer)
Pilih beberapa nilai x kemudian carilah nilai y nya
dengan menstubstitusikan nilai x pada fungsi f
Buat daftar nilai f dalam tabel
Gambar titik-titik pada bidang koordinat

29. Dengan memperhatikan nilai a dan D dari suatu fungsi
kuadrat y=f(x)= ax2+bx+c, ada 6 kemungkinan kedudukan
grafik fungsi kuadrat terhadap sumbu X.

30. Contoh
Gambarkan sketsa grafik fungsi kuadrat f(x) = -x2+2x-1
Jawab :
• Grafik fungsi kuadrat f(x) = x2+2x – 1 adalah sebuah parabola dengan
• persamaan y = x2+2x -1, berarti a= -1, b =2, dan c = -1.
(i). Titik potong grafik dengan sumbu x dan sumbu y.
a). Titik potong grafik dengan sumbu x diperoleh jika y = 0.
ini berarti: -x2-2x-1 = 0 (kedua ruas dikalikan -1)
- x2-2x+1 = 0
(x-1)(x-1) = 0
x-1 = 0 atau x-1 = 0
x = 0+1 atau x = 0+1
x = 1 atau x = 1
Jadi, titik potongnya dengan sumbu x adalah (1,0) atau grafik menyinggung
sumbu x di titik (1,0).

31. b). Titik potong grafik dengan sumbu y diperoleh jika x=0.
Ini berarti: y = -(0)2+2(0)-1
y = 0 + 0-1
y = -1
Jadi, titik potongnya dengan sumbu y adalah (0,-1).
(ii). Koordinat titik balik.
−𝑏 −2
𝑥𝑝 =
2𝑎
=
2. −1
= 1
Oleh Karena a = -1<0, maka p merupakan titik balik maksimum, sehingga
parabolanya terbuka ke bawah
2𝑎
(iii). Persamaan sumbu simetri adalahx = −𝑏
=
−2
2.−1
= 1

32. Jadi sketsa grafik fungsi kuadrat f(x) = -x2+2x-1adalah

33. Fungsi kuadrat yang grafiknya melalui tiga
buah titik
Contoh:
• Tentukan persamaan grafik fungsi
kuadrat yang melalui titik (–1 , 0) , ( 1 ,
8 ) dan ( 2, 6 ).
Jawab :
Misal persamaan grafik adalah y = a x2 +
b x + c
Grafik melalui titik (–1 , 0) ® 0 = a(–
1)2 + b (–1) + c
0 = a – b + c ………………. (1)
Grafik melalui titik (1 , 8) ®
=a (1)2 + b (1) + c
8 = a + b + c ………………. (2)
Grafik melalui titik ( 2 , 6 ) ® 6
= a (2)2 + b (2) + c
6 = 4 a + 2 b + c …………… (3)
• Dari persamaan (1), (2), dan (3) dapat
ditentukan nilai a, b, dan c dengan cara
eliminasi.

34. Fungsi kuadrat yang grafiknya memotong
sumbu-X
Misalkan titik potongnya (p , 0) dan (q , 0).
(p , 0) dan (q , 0) memenuhi persamaan y = a x2 + b x + c sehingga 0= ap2 + bp + c dan
0= aq2 + bq + c . Kedua persamaan itu dikurangkan, akan diperoleh:
0 = a(p2 – q2) + b(p – q)
b(p – q) = –a(p2 – q2)
= –a(p + q) (p – q)
b = – a(p + q)
ke ap2 + bp + c = 0
Substitusikan b = – a(p + q)
ap2 + (– a(p + q)) p + c = 0
ap2 – ap2 – pqa + c = 0
c = pqa
Untuk b = – a(p + q) dan c = pqa maka
y = a x2 + b x + c Û y = ax2 – a(p + q)x + pqa
= a(x2 – (p + q)x + pq)
= a(x – p) (x – q)
Jadi, y = a(x – p) (x – q) adalah fungsi kuadrat yang grafiknya memotong sumbu-X di (p,0)
dan (q,0).

35. • Contoh:
Tentukan fungsi kuadrat yang grafiknya memotong sumbu-X di titik (5,0)
dan (1,0), serta melalui titik (–3, –8) !
• Jawab:
y = x2 +
Grafik memotong sumbu-X di titik (–5,0) dan (1,0), maka fungsi
kuadratnya
y = a(x – (–5)) (x – 1)
= a(x + 5) (x – 1)
Grafik melalui titik (–3, –8), berarti
–8 = a(–3+5) (–3 – 1)
= –8a
a = 1
Substitusikan a = 1 pada y = a(x + 5) (x – 1) sehingga diperoleh
4x – 5.

36. • Menentukan fungsi kuadrat jika koordinat titik puncak grafik fungsi itu
diketahui
Koordinat titik tertinggi/ terendah grafik fungsi kuadrat y = ax2 + bx + c adalah .
Dengan melihat kembali kajian terdahulu, maka fungsi kuadrat y = ax2 + bx + c dapat
dinyatakan dengan .
Sehingga fungsi kuadrat yang berpuncak di (p , q) adalah y = a (x – p)2 + q
• Contoh:
Tentukan fungsi kuadrat yang grafiknya mempunyai titik tertinggi (1,3) dan melalui titik
(0,0).
Jawab:
Fungsi kuadrat yang grafiknya berpuncak di (1,3) adalah y = (x – 1)2 + 3
Grafik melalui titik (0,0) berarti:
0 = a(0 – 1) + 3
0 = a + 3
a = –3
y = a (x – 1)2 + 3 maka diperoleh
Substitusikan a = –3 pada
y = –3 (x – 1)2 + 3
y = –3 (x2 – 2x + 1) + 3
y = –3x2 + 6x
Jadi, fungsi kuadratnya adalah y = –3x2 + 6x.

37. Fungsi kuadrat yang grafiknya menyinggung sumbu-X
• Perhatikan kembali bahasan tentang “Titik potong grafik dengan sumbu-X”. Grafik
akan menyinggung sumbu-X jika dan hanya jika b2 – 4ac = 0, maka koordinat titik
tertinggi atau terendah adalah (x,0).
Sehingga .
Jadi, fungsi kuadrat yang grafiknya menyinggung sumbu-X adalah .
Sehingga fungsi kuadrat yang grafiknya menyinggung sumbu X adalah y = a(x – p)2
• Contoh:
Tentukan fungsi kuadrat yang grafiknya menyinggung sumbu-X di titik (2,0) dan melalui
titik (0,4) !
Jawab:
Fungsi kwadrat yang grafiknya menyinggung sumbu X di (2,0) adalah
y = a (x – 2)2
Grafik melalui titik (0,4) berarti :
4 = a(0 – 2)2 = 4a
a = 1
Jadi, fungsi kuadrat itu y = 1(x – 2)2 atau y = x2 – 4x + 4.