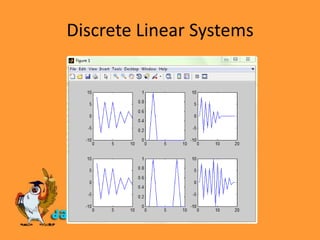
Discrete linear systems are digital implementations of linear time-invariant systems. They can be represented using various models including transfer functions, state-space models, and convolution matrices. Common transfer function representations include zero-pole-gain form and partial fraction expansion. Filters can also be modeled using second-order sections or lattice/ladder structures.

1. Discrete Linear Systems

2. Discrete Linear SystemsA discrete linear system is a digital implementation of a linear time-invariant system. A linear system is a mathematical model of a system based on the use of a linear operator. Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case.

3. Discrete Linear Systems>> A=[8 -7 6 -5 6 -5 2 -3 2 -1];x=[0 1 0 0 0 0 0 0 0 0 ];B=conv(A,x);subplot(2,3,1); plot(A);subplot(2,3,2); plot(x);subplot(2,3,3); plot(B);x=[0 1 0 0 0 0 0 1 0 0 ];B=conv(A,x);subplot(2,3,4); plot(A);subplot(2,3,5); plot(x);subplot(2,3,6); plot(B);

4. Discrete Linear Systems

5. Discrete-Time System ModelsTransfer FunctionZero-Pole-GainState-SpacePartial Fraction Expansion (Residue Form)Second-Order Sections (SOS)Lattice StructureConvolution Matrix

6. Discrete-Time System ModelsThe transfer functionis a basic z-domain representation of a digital filter, expressing the filter as a ratio of two polynomials.

7. Discrete-Time System ModelsThe factored or zero-pole-gain form of a transfer function is

8. Discrete-Time System ModelsIt is always possible to represent a digital filter, or a system of difference equations, as a set of first-order difference equations. In matrix or state-space form, we can write the equations as

9. Discrete-Time System ModelsEach transfer function also has a corresponding partial fraction expansion or residue form representation, given by

10. Discrete-Time System ModelsAny transfer function H(z) has a second-order sections representation

11. Discrete-Time System ModelsThe function latc2tf calculates the polynomial coefficients for a filter from its lattice (reflection) coefficients. Given the reflection coefficient vector k(above), the corresponding polynomial form isb = latc2tf(k) b = 1.0000 0.6149 0.9899 -0.0000 0.0031 -0.0082 The lattice or lattice/ladder coefficients can be used to implement the filter using the function latcfilt.

12. Discrete-Time System ModelsGiven any vector, the toolbox function convmtx generates a matrix whose inner product with another vector is equivalent to the convolution of the two vectors. The generated matrix represents a digital filter that you can apply to any vector of appropriate length; the inner dimension of the operands must agree to compute the inner product.

13. Visit more self help tutorialsPick a tutorial of your choice and browse through it at your own pace.The tutorials section is free, self-guiding and will not involve any additional support.Visit us at www.dataminingtools.net