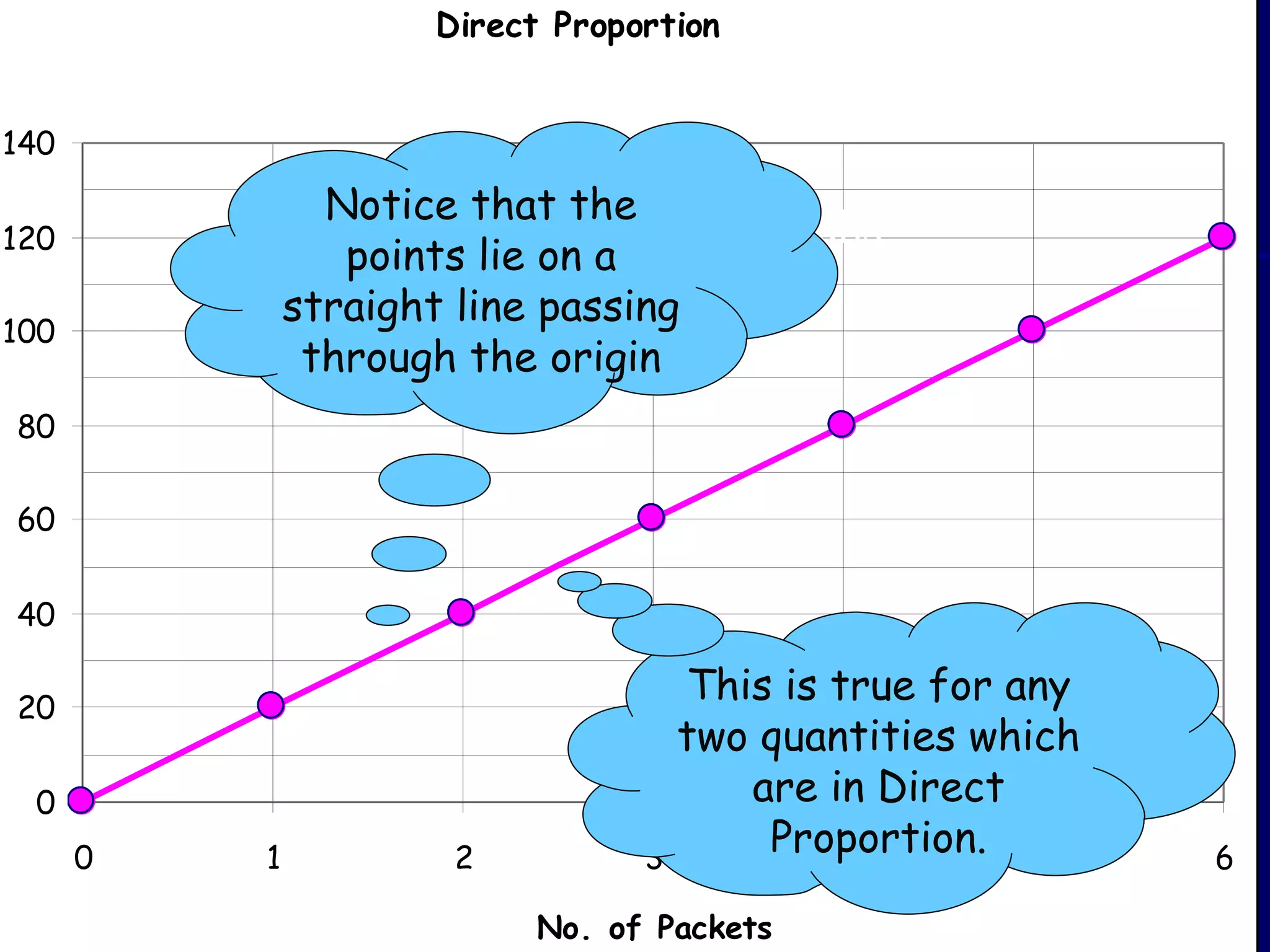
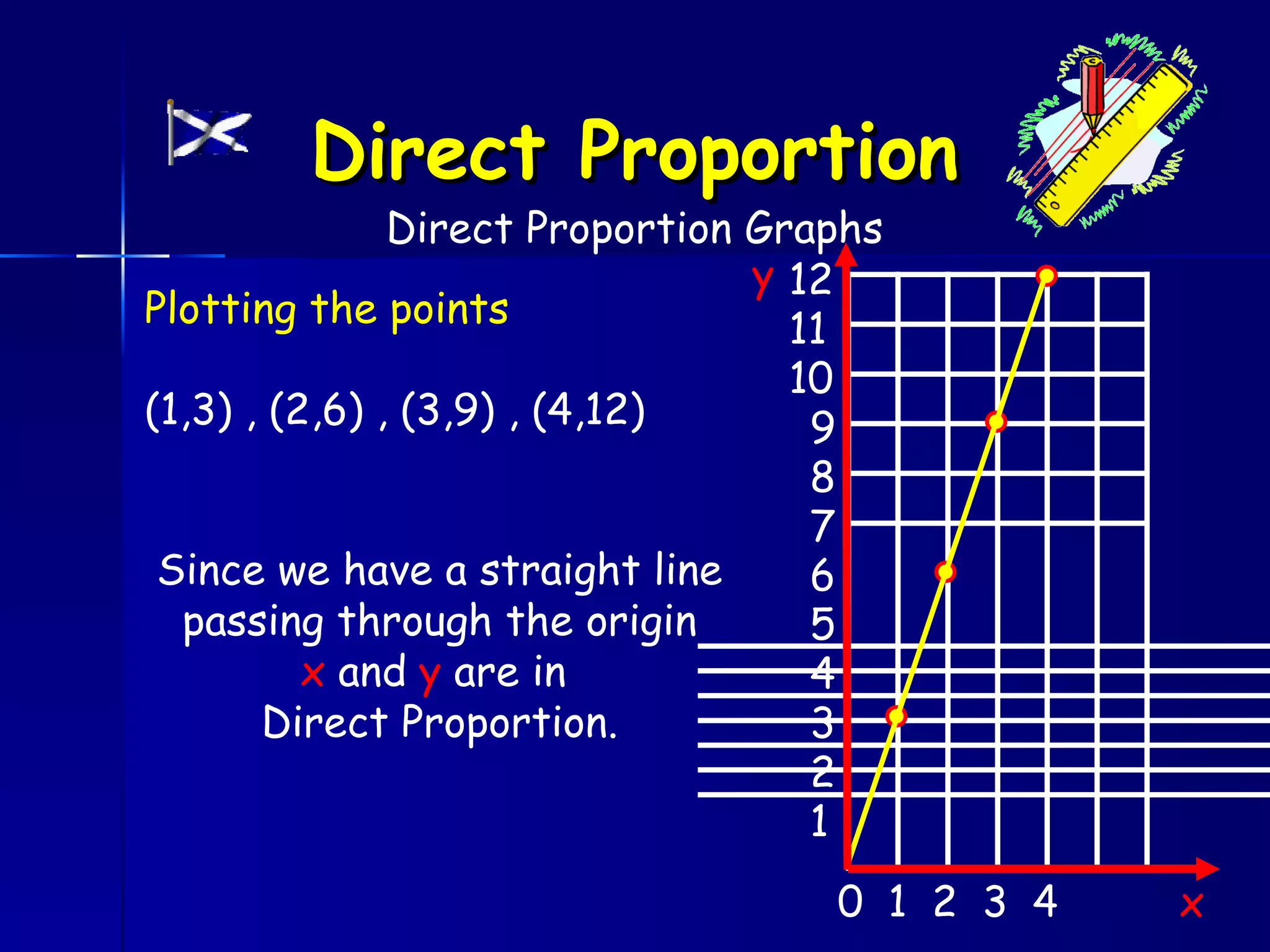
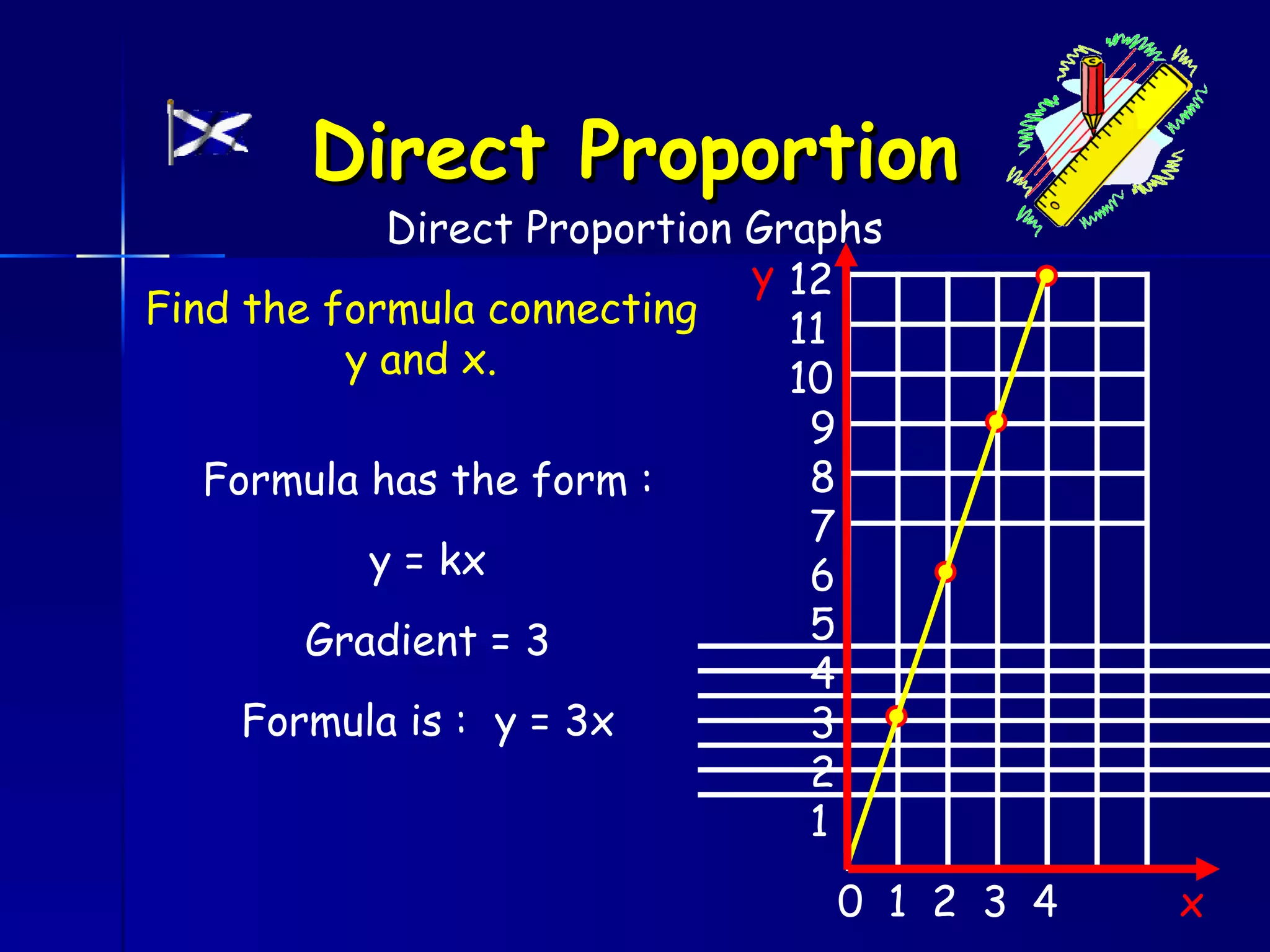
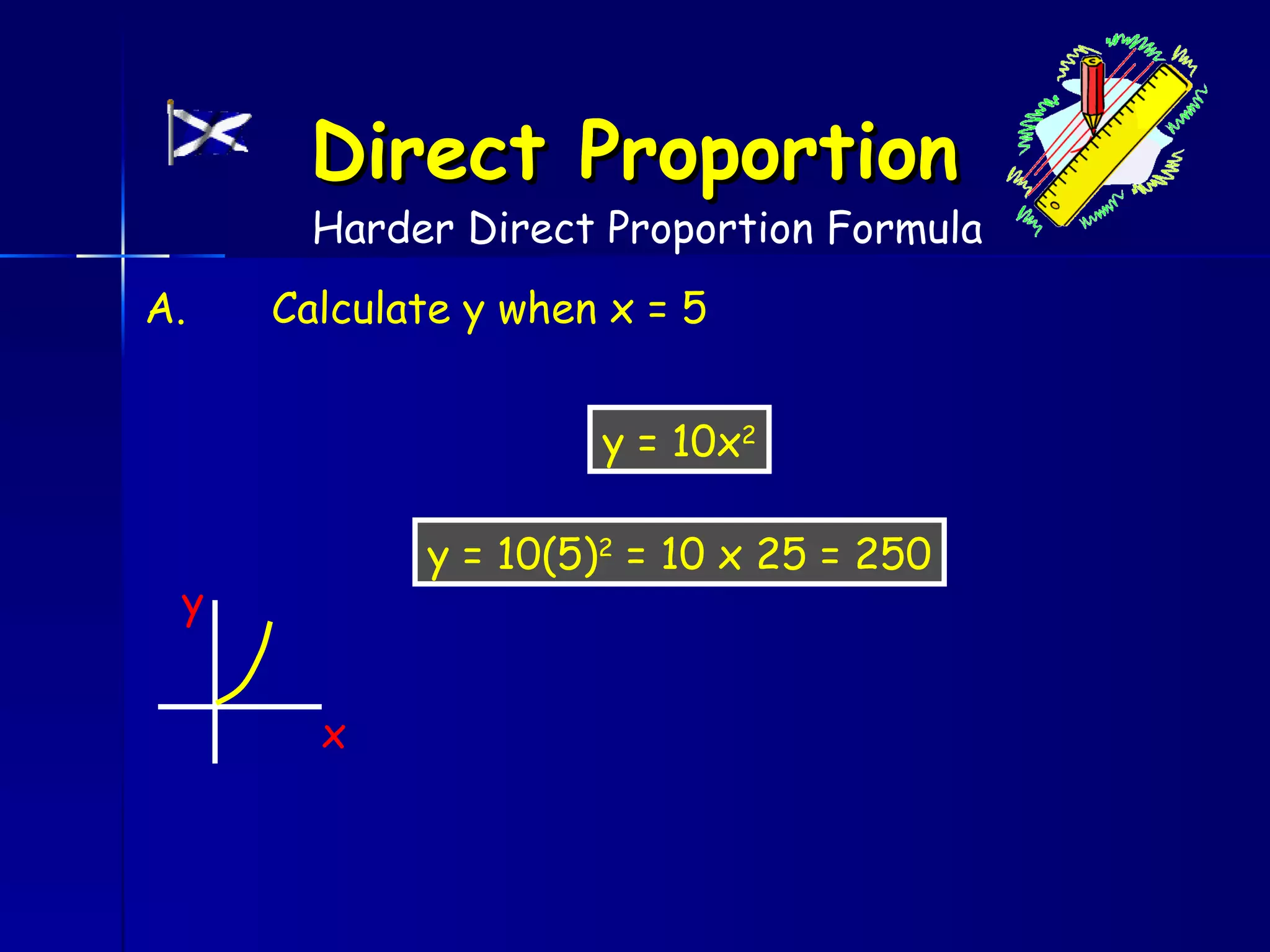
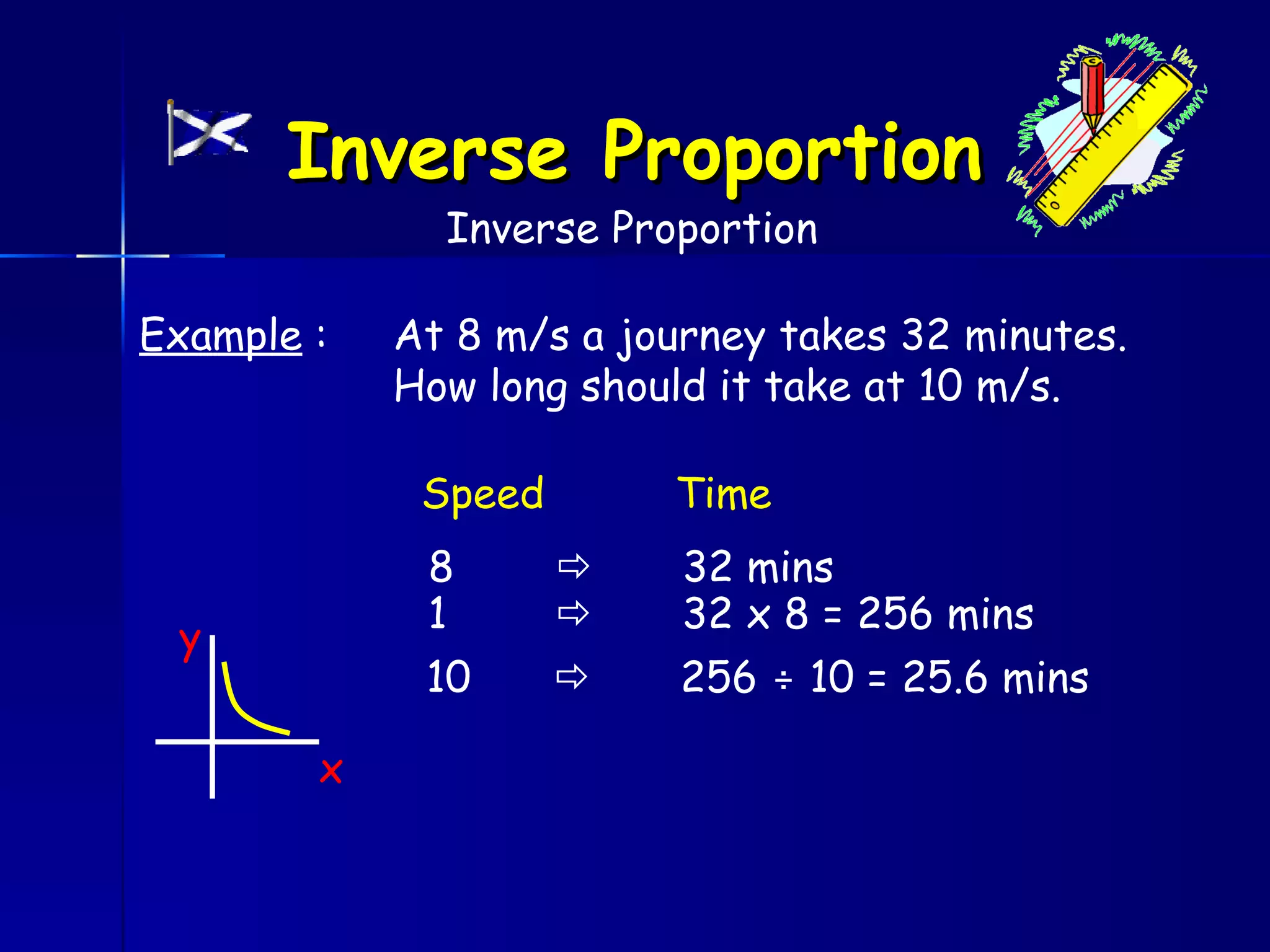
The document discusses direct and inverse proportions. It provides examples of quantities that are directly proportional, such as cost and number of items. Directly proportional quantities follow the relationship that if one quantity doubles, the other will double as well. They form a straight line passing through the origin on a graph. Inverse proportions occur when one quantity increases as the other decreases, such as time taken to complete a task with more workers. Formulas are provided to represent direct and inverse proportional relationships between variables.

1. Direct Proportion
Direct Proportion
Direct Proportion Graphs
Direct Proportion formula and calculations
Other Direct Proportion formula
Inverse Direct Proportion

2. Direct Proportion
Direct Proportion
Two quantities, (for example, number of cakes and total
cost) are said to be in DIRECT Proportion, if :
“ .. When you double the number of cakes
you double the cost.”
Example : The cost of 6 cakes is £4.20. find the cost
of 5 cakes.
Cakes Cost
Write down two 6  4.20
quantities that are 1  4.20 ÷ 6 = 0.70
in direct
proportion. 5  0.70 x 5 = £3.50

3. Direct Proportion
Direct Proportion
Example : On holiday I exchanged £30 for $45.
How many $ will I get for £50.
What name do
Exchang
we give to this £ $
value e rate
30  45
1  45 ÷ 30 = 1.5
50  1.5 x 50 = $75

4. Direct Proportion
Direct Proportion
Example : To make scrambled eggs for 2 people
we need 2eggs, 4g butter and 40 ml of milk.
How much of each for
(a) 4 people (b) Just himself
(a) Simply multiple by 2 :
4 eggs, 8g butter, 80 ml of milk.
(b) Simply half original amounts:
1 eggs, 2g butter, 20 ml of milk.

5. Direct Proportion
Direct Proportion Graphs
The table below shows the cost of packets of “Biscuits”.
No. of Pkts 1 2 3 4 5 6
Cost (p) 20 40 60 80 100 120
We can construct a graph to represent this data.
What type of graph do we expect ?

6. Direct Proportion
140
Notice that the
120 Direct Proportion Graphs
points lie on a
straight line passing
100
through the origin
80
60
40
20
This is true for any
two quantities which
0 are in Direct
0 1 2 3
Proportion. 5
4 6
May 11, 2012 Created by Mr. Lafferty Maths Dept.
No. of Packets

7. Direct Proportion
Direct Proportion Graphs
KeyPoint
Two quantities which are in
Direct Proportion
always lie on a straight line
passing through the origin.

8. Direct Proportion
Direct Proportion Graphs
Example : Plot the points in the table below.
Are they in Direct Proportion?
X 1 2 3 4
y 3 6 9 12
We plot the points (1,3) , (2,6) , (3,9) , (4,12)

9. Direct Proportion
Direct Proportion Graphs
y 12
Plotting the points 11
10
(1,3) , (2,6) , (3,9) , (4,12) 9
8
7
Since we have a straight line 6
passing through the origin 5
x and y are in 4
Direct Proportion. 3
2
1
0 1 2 3 4 x

10. Direct Proportion
Direct Proportion Graphs
y 12
Find the formula connecting 11
y and x. 10
9
Formula has the form : 8
7
y = kx 6
Gradient = 3 5
4
Formula is : y = 3x 3
2
1
0 1 2 3 4 x

11. Direct Proportion
Direct Proportion Graphs
Important facts:
Fill in table
Find gradient from graph
Write down formula using knowledge
from straight line chapter

12. Direct Proportion
Direct Proportion Formula
• Given that y is directly proportional to x,
and when y = 20, x = 4.
Find a formula connecting y and x
Since y is directly proportional to x
the formula is of the form
y = kx k is the
gradient
20 = k(4)
k = 20 ÷ 4 = 5
y = 5x

13. Direct Proportion
Direct Proportion Formula
• The number of dollars (d) varies directly as the
number of £’s (P). You get 3 dollars for £2.
Find a formula connecting d and P.
Since d is directly proportional to P
the formula is of the form
d = kP k is the
gradient
3 = k(2)
k = 3 ÷ 2 = 1.5
d = 1.5P

14. Direct Proportion
Direct Proportion Formula
A. How much will I get for £20
d = 1.5P
d = 1.5 x 20 = 30 dollars

15. Direct Proportion
Harder Direct Proportion Formula
• Given that y is directly proportional to the square
of x, and when y = 40, x = 2.
Find a formula connecting y and x when .
Since y is directly proportional to x squared
the formula is of the form
y
y = kx2
x 40 = k(2)2
k = 40 ÷ 4 = 10
y = 10x2

16. Direct Proportion
Harder Direct Proportion Formula
A. Calculate y when x = 5
y = 10x2
y = 10(5)2 = 10 x 25 = 250
y
x

17. Direct Proportion
Harder Direct Proportion Formula
A. The cost (C) of producing a football magazine
varies as the square root of the number of
pages (P). Given 36 pages cost 45p to produce.
Find a formula connecting C and P.
Since C is directly proportional to “square root of” P
the formula is of the form
y C =k P
48 = k 36
x k = 48 ÷ 6 = 8
C =8 P

18. Direct Proportion
Harder Direct Proportion Formula
A. How much will 100 pages cost.
C = 8 100
C = 8 100 = 8 × 10 = 80p
y
x

19. Inverse Proportion
Inverse Proportion
Inverse Proportion is when one quantity increases
and the other decreases. The two quantities are said
to be INVERSELY Proportional
or (INDIRECTLY Proportional) to each other.
Example : Fill in the following table given x and y
are inversely proportional.
y
X 1 2 4 8
y 80 40 20 10
x

20. Inverse Proportion
Inverse Proportion
Inverse Proportion is the when one quantity increases
and the other decreases. The two quantities are said
to be INVERSELY Proportional
or (INDIRECTLY Proportional) to each other.
Example : If it takes 3 men 8 hours to build a wall.
How long will it take 4 men. (Less time !!)
y Men Hours
3  8
x 1  3 x 8 = 24 hours
4  24 ÷ 4 = 6 hours

21. Inverse Proportion
Inverse Proportion
Example : It takes 10 men 12 months to build a house.
How long should it take 15 men.
Men Months
10  12
1  12 x 10 = 120
y
15  120 ÷ 15 = 8 months
x

22. Inverse Proportion
Inverse Proportion
Example : At 8 m/s a journey takes 32 minutes.
How long should it take at 10 m/s.
Speed Time
8  32 mins
1  32 x 8 = 256 mins
y
10  256 ÷ 10 = 25.6 mins
x