1) The document discusses different ways to convert between fractions, decimals, and percentages including using place value, cancelling fractions, finding equivalent fractions, and dividing the numerator by the denominator. 2) Methods are presented for calculating percentages of amounts using mental math for simple percentages, changing the percentage to an equivalent fraction, and changing it to a decimal. The concepts of percentage increase and decrease are also explained. 3) Proportions are defined as comparing the size of a part to the whole, and examples are given of expressing proportions as fractions, decimals, and percentages. 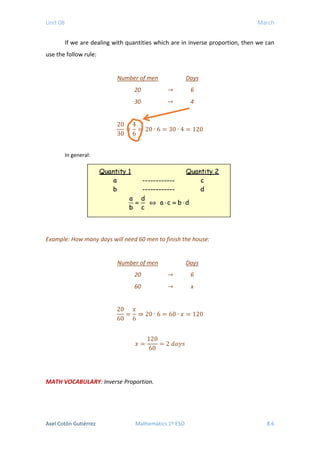4) Direct and inverse proportion are introduced, with direct proportion meaning quantities increase in the same ratio and inverse proportion meaning they decrease in the

1. Unit 08 March
1. FRACTION, DECIMAL AND PERCENTAGE EQUIVALENTS.
All these amounts show part of a whole:
𝟑𝟑
𝟒𝟒
; 𝟎𝟎. 𝟕𝟕𝟕𝟕; 𝟕𝟕𝟕𝟕%
A Percentage is a fraction written as a number of parts per 100.
37% =
37
100
; 154% =
154
100
You should be able to convert between fractions, decimals and percentages:
• Using Place Value:
37% =
37
100
= 0.37
• Cancelling fractions:
75% =
75
100
=
3
4
• Finding an equivalent fraction:
2
5
=
40
100
= 40%
• By dividing the numerator by the denominator of a fraction:
2
5
= 2 ÷ 5 = 0.4
Once you change a fraction to a decimal you can easily convert it to a
percentage. You just multiply the decimal by 100.
2
5
= 2 ÷ 5 = 0.4 = 40%
MATH VOCABULARY: Percentage.
Axel Cotón Gutiérrez Mathematics 1º ESO 8.1

2. Unit 08 March
2. PERCENTAGES OF AMOUNTS.
You can calculate the Percentage of an Amount using mental methods, using
an equivalent fraction or using an equivalent decimal.
• Use mental methods to find simple percentages:
50% 𝑜𝑜𝑜𝑜 400
⇒ 50% 𝑜𝑜𝑜𝑜 𝑎𝑎 𝑞𝑞𝑞𝑞𝑞𝑞𝑞𝑞𝑞𝑞𝑞𝑞𝑞𝑞𝑞𝑞 𝑖𝑖𝑖𝑖 𝑡𝑡ℎ𝑒𝑒 𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 𝑎𝑎𝑎𝑎 𝑜𝑜𝑜𝑜𝑜𝑜 ℎ𝑎𝑎𝑎𝑎𝑎𝑎 𝑜𝑜𝑜𝑜 𝑡𝑡ℎ𝑎𝑎𝑎𝑎 𝑞𝑞𝑞𝑞𝑞𝑞𝑞𝑞𝑞𝑞𝑞𝑞𝑞𝑞𝑞𝑞,
𝑠𝑠𝑠𝑠 50% 𝑜𝑜𝑜𝑜 400 = 200
• Change the percentage to its equivalent fraction and multiply by the amount:
9% 𝑜𝑜𝑜𝑜 24 𝑚𝑚 =
9
100
𝑜𝑜𝑜𝑜 24𝑚𝑚 =
9 ∙ 24
100
=
216
100
= 2.16 𝑚𝑚
• Change the percentage to its equivalent decimal and multiply by the amount:
35% 𝑜𝑜𝑜𝑜 £90 =
35
100
𝑜𝑜𝑜𝑜 £90 = 0.35 ∙ 90 = £31.5
(0.35 is the Decimal Equivalent of 35%)
MATH VOCABULARY: Decimal Equivalent.
3. PERCENTAGE INCREASE AND DECREASE.
You can add on a Percentage Increase or subtract a Percentage Decrease at the
end of the calculation.
Example 1: A plane ticket to Rome cost, last summer, € 460, but has since risen 20%.
What is the current price of the ticket?
𝑂𝑂𝑂𝑂𝑂𝑂 𝑂𝑂𝑂𝑂𝑂𝑂𝑂𝑂𝑂𝑂 𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝 = € 460 𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃 𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖 = 20%
𝐼𝐼𝐼𝐼𝐼𝐼𝐼𝐼𝐼𝐼𝐼𝐼𝐼𝐼𝐼𝐼 = 20% 𝑜𝑜𝑜𝑜 𝑡𝑡ℎ𝑒𝑒 𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜 𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝 = 20% 𝑜𝑜𝑜𝑜 € 460 = € 92
𝑁𝑁𝑁𝑁𝑁𝑁 𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝 = 𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜 𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝 + 𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖 = € 460 + € 92 = € 552
Axel Cotón Gutiérrez Mathematics 1º ESO 8.2

3. Unit 08 March
Example 2: A discount store offers 15% cheaper clothing. A dress cost before € 50, How
much does it cost now?
𝑂𝑂𝑂𝑂𝑂𝑂 𝑂𝑂𝑂𝑂𝑂𝑂𝑂𝑂𝑂𝑂 𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝 = € 50 𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃 𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖 = 15%
𝐷𝐷𝑒𝑒𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐 = 15% 𝑜𝑜𝑜𝑜 𝑡𝑡ℎ𝑒𝑒 𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜 𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝 = 15% 𝑜𝑜𝑜𝑜 € 50 = € 7.5
𝑁𝑁𝑁𝑁𝑁𝑁 𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝 = 𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜 𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝 − 𝑑𝑑𝑑𝑑𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐 = € 50 − € 7.5 = € 42.5
Alternatively you can calculate the percentage increase or decrease in a single
calculation.
Example 1:
𝑁𝑁𝑁𝑁𝑁𝑁 𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝 = (100 + 20)% 𝑜𝑜𝑜𝑜 𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜 = 120% 𝑜𝑜𝑜𝑜 €460 = 1.2 · €460 = €552
Example 2:
𝑁𝑁𝑁𝑁𝑁𝑁 𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝 = (100 − 15)% 𝑜𝑜𝑜𝑜 𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜 = 85% 𝑜𝑜𝑜𝑜 €50 = 0.85 · €50 = €42.5
MATH VOCABULARY: Percentage Increase, Percentage Decrease.
4. PROPORTION.
A Proportion compares the size of the part (or portion) to the size of the whole.
In a class of 26, 11 are girls and 15 are boys. The proportion of girls is 11 out of
26. The proportion of boys is 15 out of 26.
You can express a proportion as a fraction, a decimal or a percentage.
𝑃𝑃𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟 𝑜𝑜𝑓𝑓 𝑔𝑔𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖 =
11
26
= 0.4231 = 42.31%
𝑃𝑃𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟 𝑜𝑜𝑓𝑓 𝑏𝑏𝑏𝑏𝑏𝑏𝑏𝑏 =
15
26
= 0.5769 = 57.69%
MATH VOCABULARY: Proportion.
Axel Cotón Gutiérrez Mathematics 1º ESO 8.3

4. Unit 08 March
5. DIRECT PROPORTION.
When an increase in one quantity means another quantity increases in the
same proportion, the quantities are in Direct Proportion. If 𝒙𝒙 and 𝒚𝒚 are in direct
proportion, then the division of 𝒙𝒙 and 𝒚𝒚 will be Constant:
𝒙𝒙
𝒚𝒚
= 𝒌𝒌 = 𝒄𝒄𝒄𝒄𝒄𝒄𝒄𝒄𝒄𝒄𝒄𝒄𝒄𝒄𝒄𝒄
Example: The number of basketballs and their price:
Number 1 2 3 4 5 6
Cost (€) 5 10 15 20 25 30
𝑥𝑥
𝑦𝑦
=
5
1
=
10
2
=
15
3
=
20
4
=
25
5
=
30
6
= 5 = 𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐
Hence, if we are dealing with quantities which are in direct proportion, then we
can use the follow rule:
Cost (€) Number
5 → 1
10 → 2
5
10
=
1
2
⇒ 10 ∙ 1 = 5 ∙ 2
In general:
Axel Cotón Gutiérrez Mathematics 1º ESO 8.4

5. Unit 08 March
Example: How much will 135 basketballs cost?
Cost (€) Number
5 → 1
x → 100
5
𝑥𝑥
=
1
100
⇒ 5 ∙ 100 = 1 ∙ 𝑥𝑥 = 500
𝑥𝑥 =
500
1
= 500€
MATH VOCABULARY: Direct Proportion, Constant.
6. INVERSE PROPORTION.
When an increase in one quantity means another quantity decreases in the
same proportion, the quantities are in Inverse Proportion. If 𝒙𝒙 and 𝒚𝒚 are in inverse
proportion, then the product of 𝒙𝒙 and 𝒚𝒚 will be Constant:
𝒙𝒙 ∙ 𝒚𝒚 = 𝒌𝒌 = 𝒄𝒄𝒄𝒄𝒄𝒄𝒄𝒄𝒄𝒄𝒄𝒄𝒄𝒄𝒄𝒄
Example: Suppose that 20 men build a house in 6 days. If men are increased to 30 then
take 4 days to build the same house. If men become 40, they take 3 days to build the
house.
Number 20 30 40
Days 6 4 3
𝑥𝑥 ∙ 𝑦𝑦 = 20 ∙ 6 = 30 ∙ 4 = 40 ∙ 3 = 120 = 𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐
Axel Cotón Gutiérrez Mathematics 1º ESO 8.5

6. Unit 08 March
If we are dealing with quantities which are in inverse proportion, then we can
use the follow rule:
Number of men Days
20 → 6
30 → 4
20
30
=
4
6
⇒ 20 ∙ 6 = 30 ∙ 4 = 120
In general:
Example: How many days will need 60 men to finish the house:
Number of men Days
20 → 6
60 → x
20
60
=
𝑥𝑥
6
⇒ 20 ∙ 6 = 60 ∙ 𝑥𝑥 = 120
𝑥𝑥 =
120
60
= 2 𝑑𝑑𝑎𝑎𝑎𝑎𝑎𝑎
MATH VOCABULARY: Inverse Proportion.
Axel Cotón Gutiérrez Mathematics 1º ESO 8.6