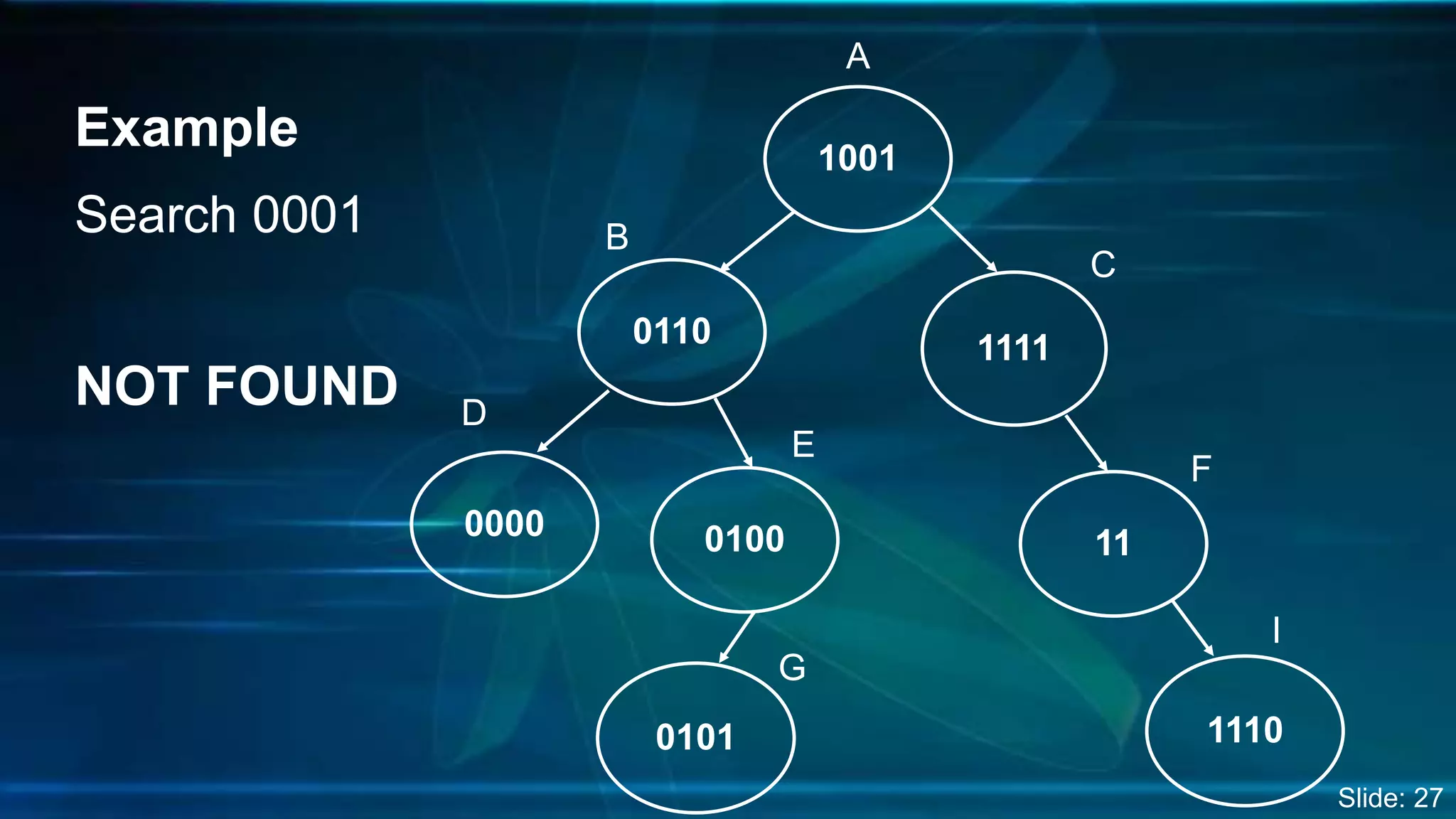
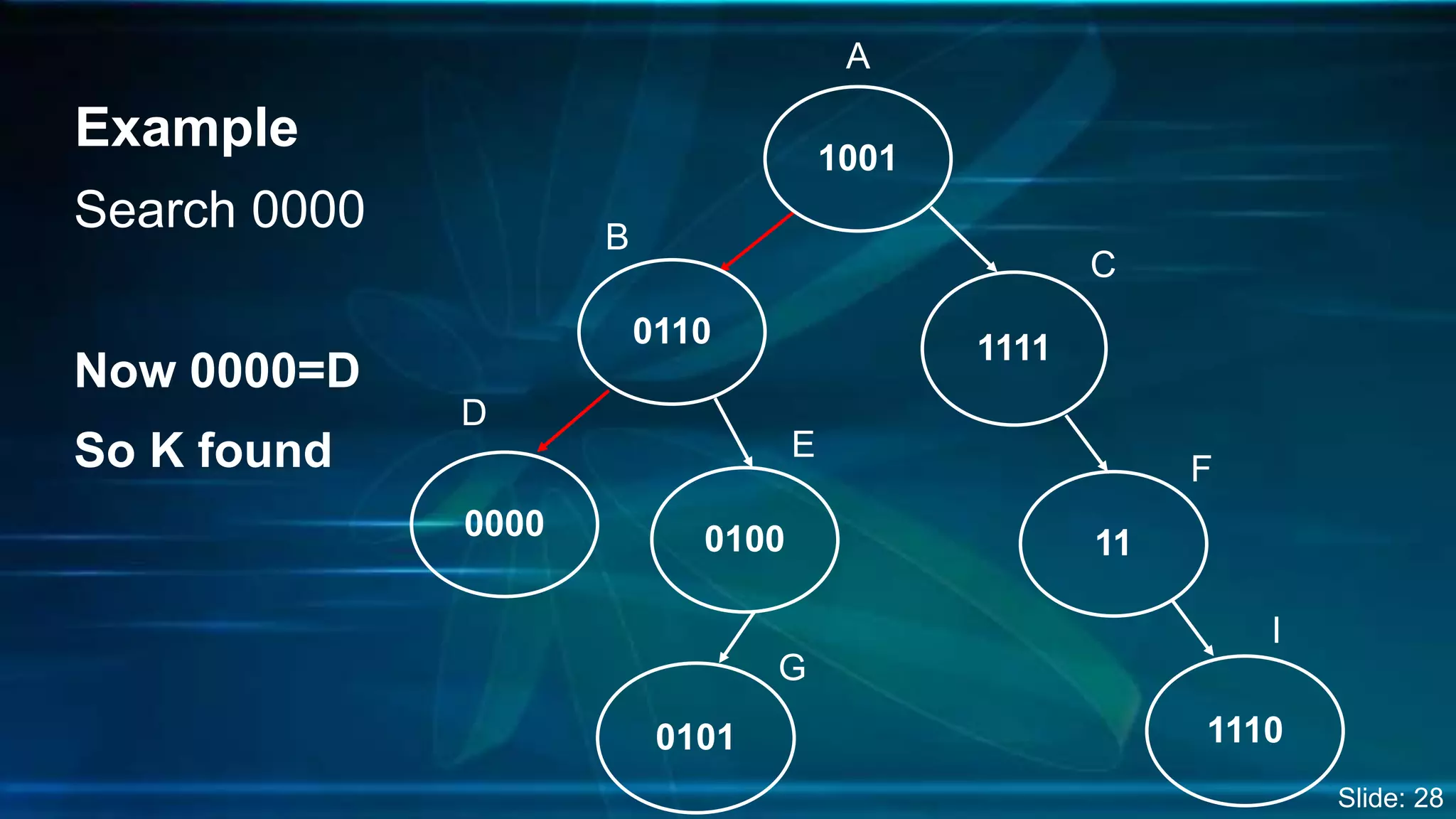
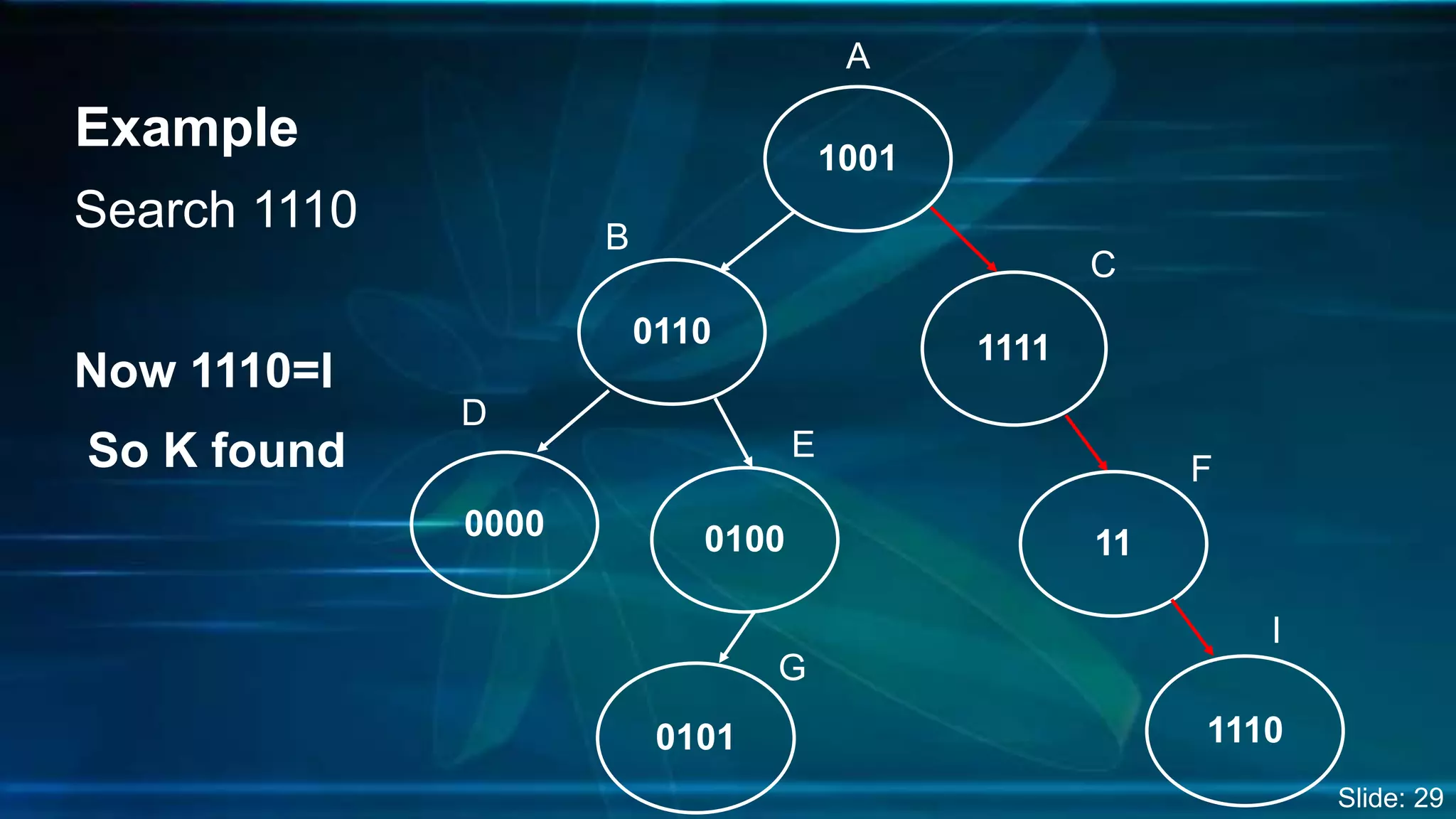
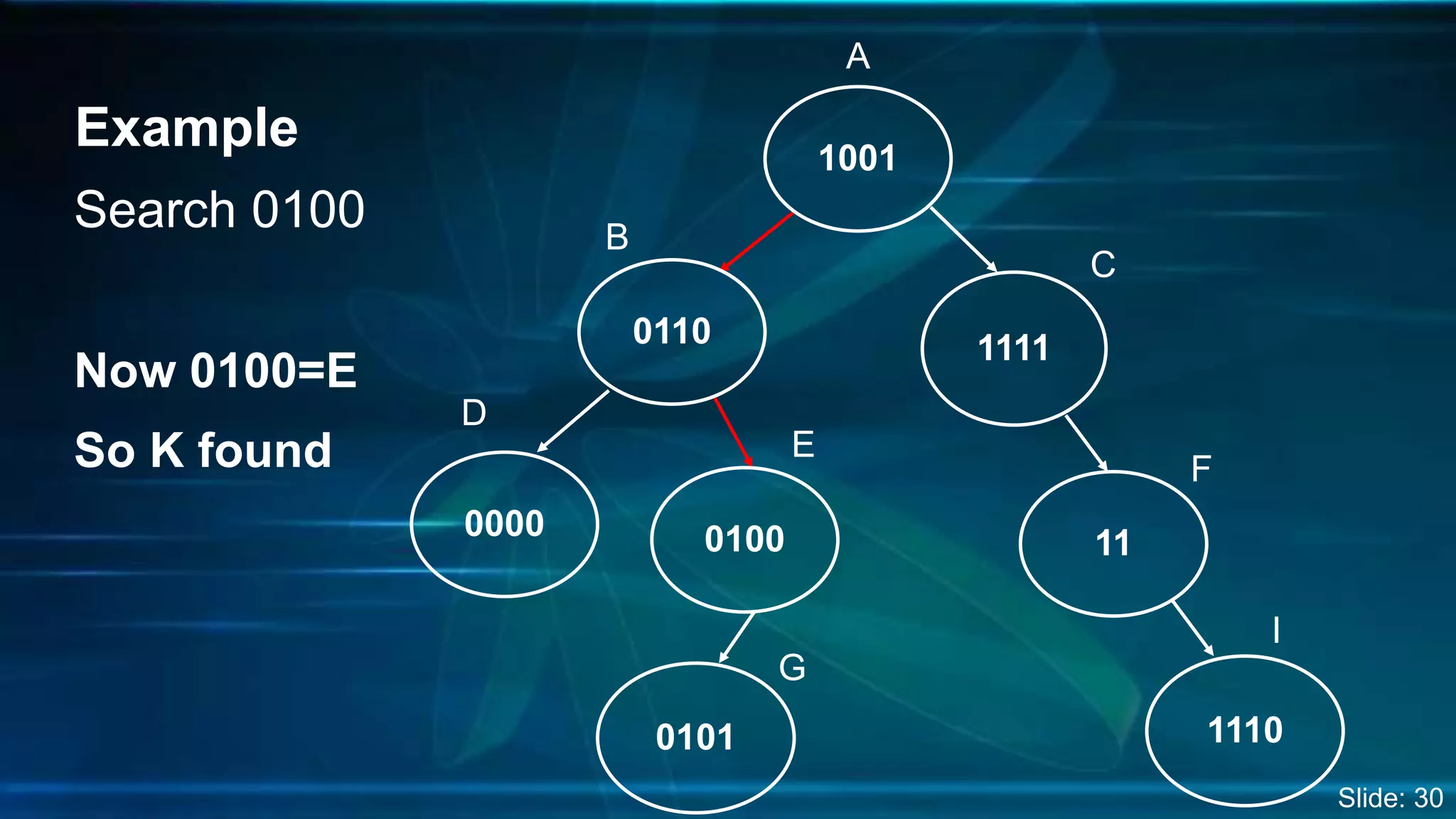
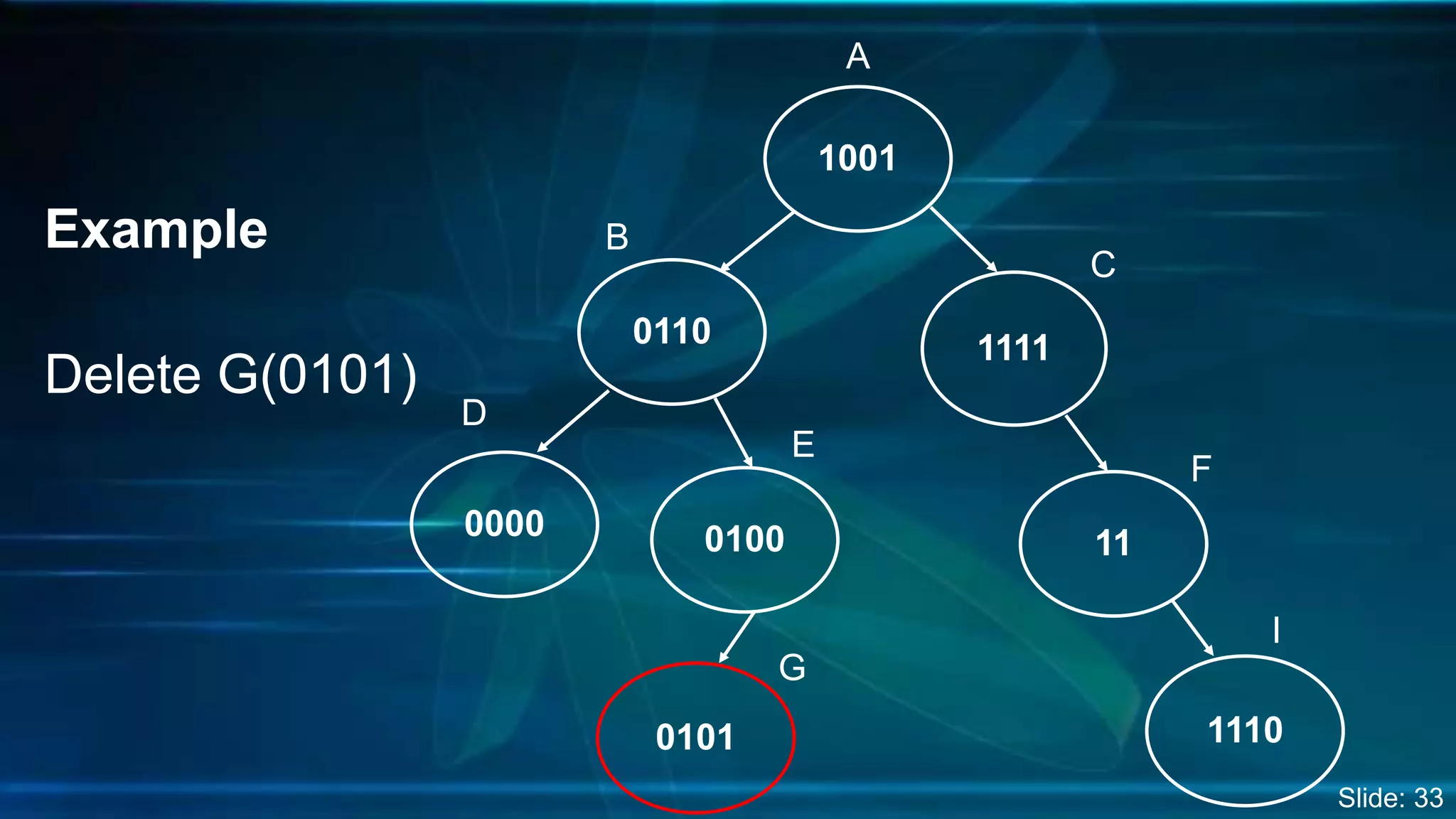
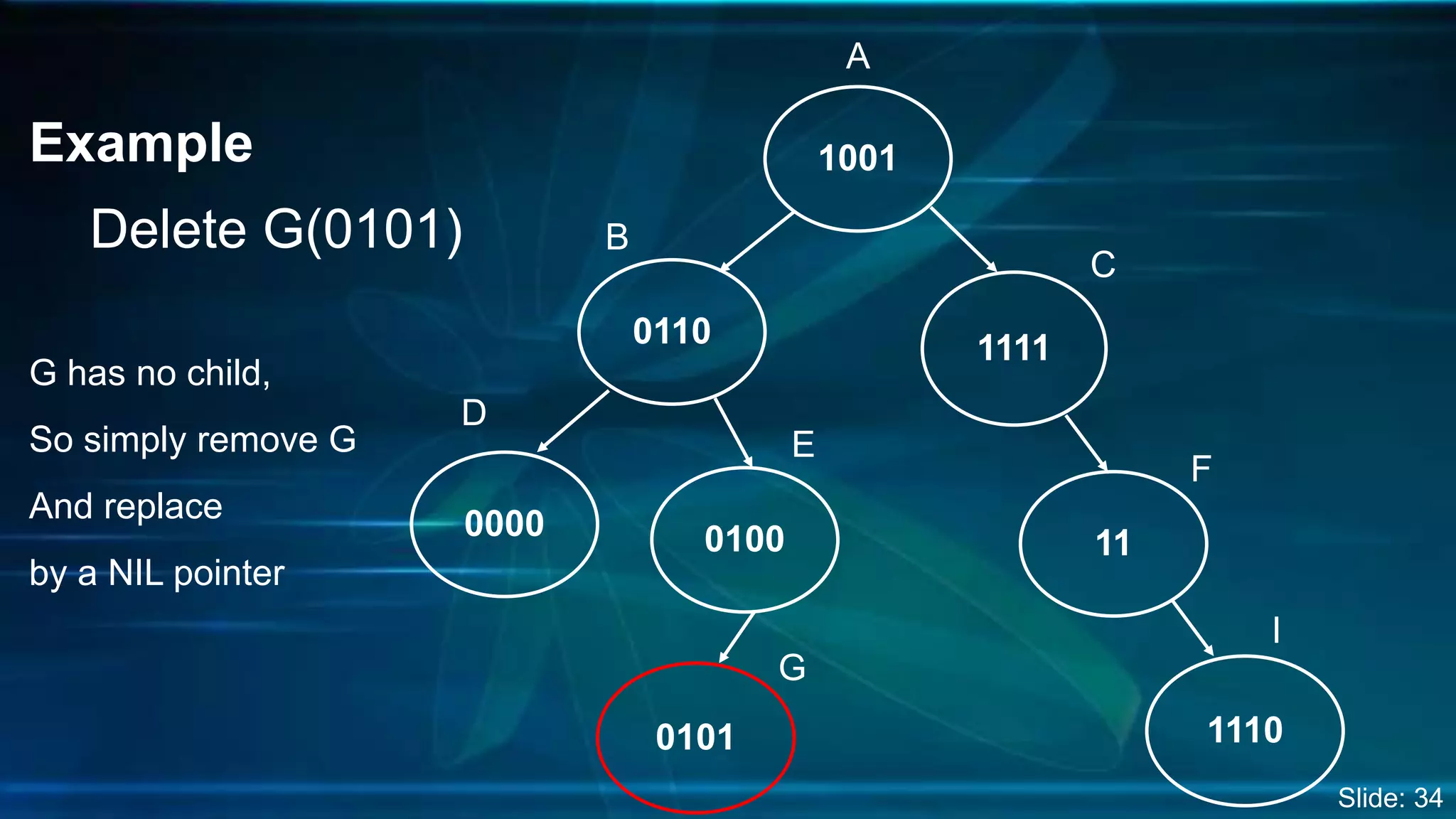
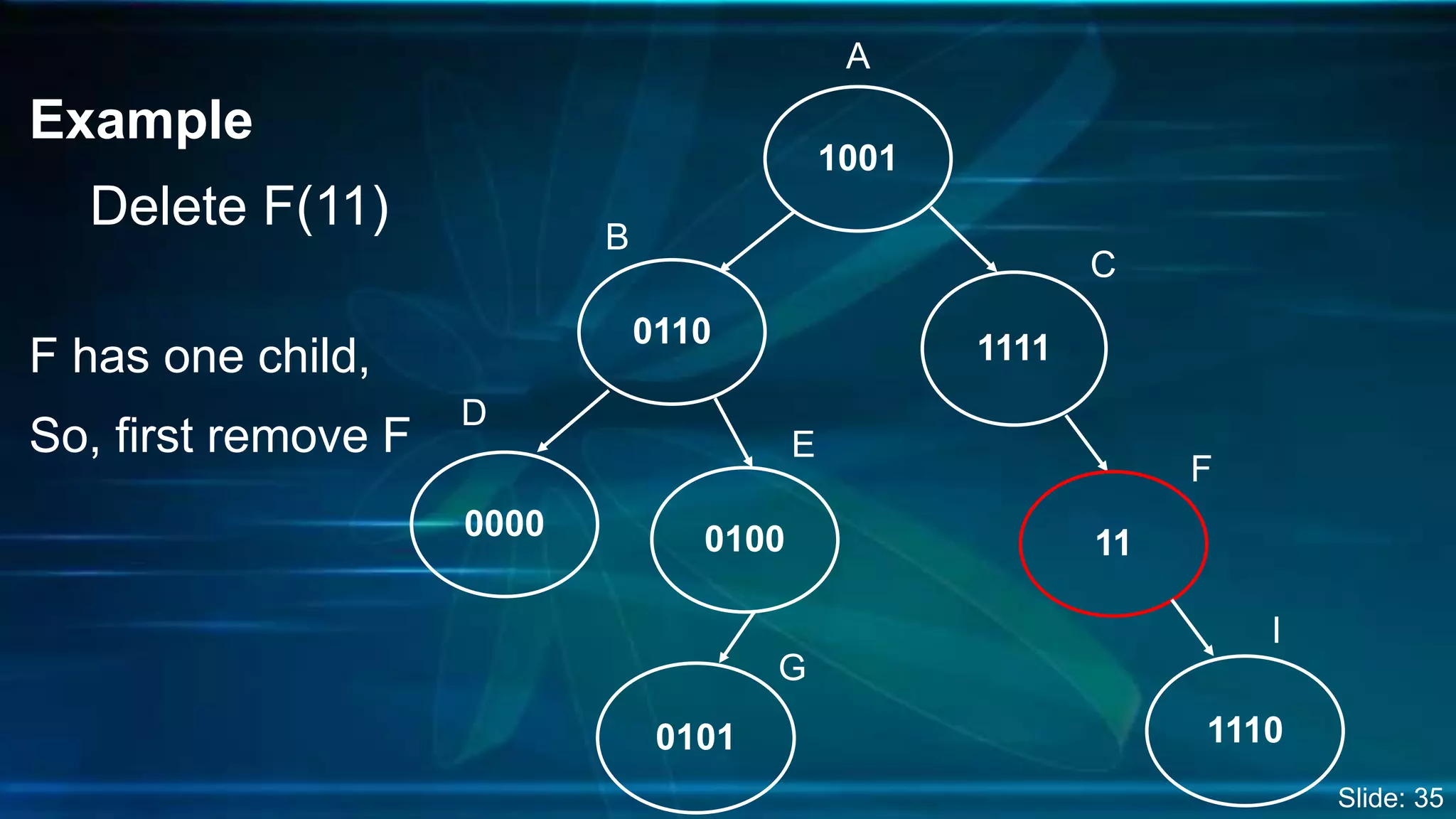
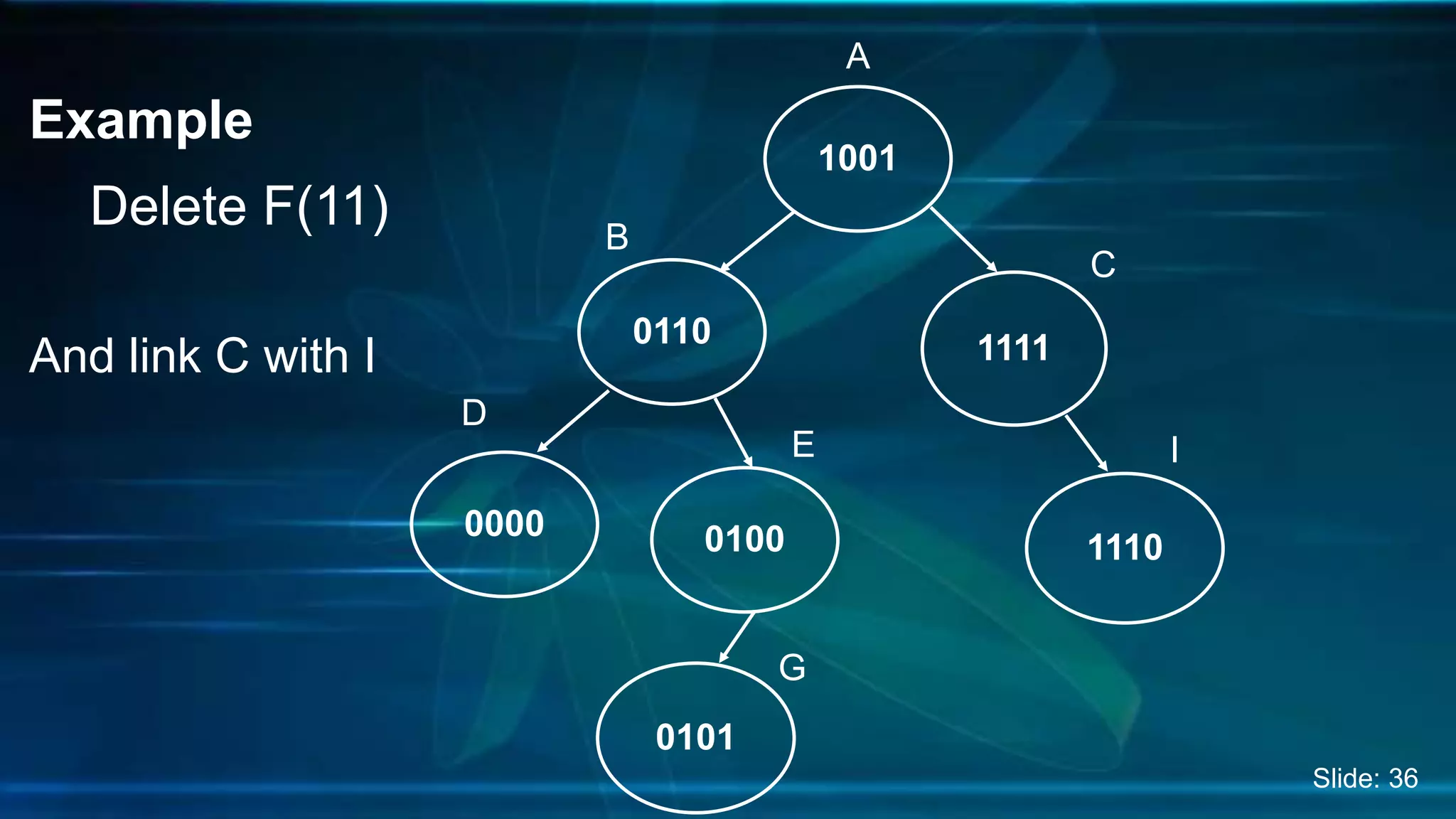
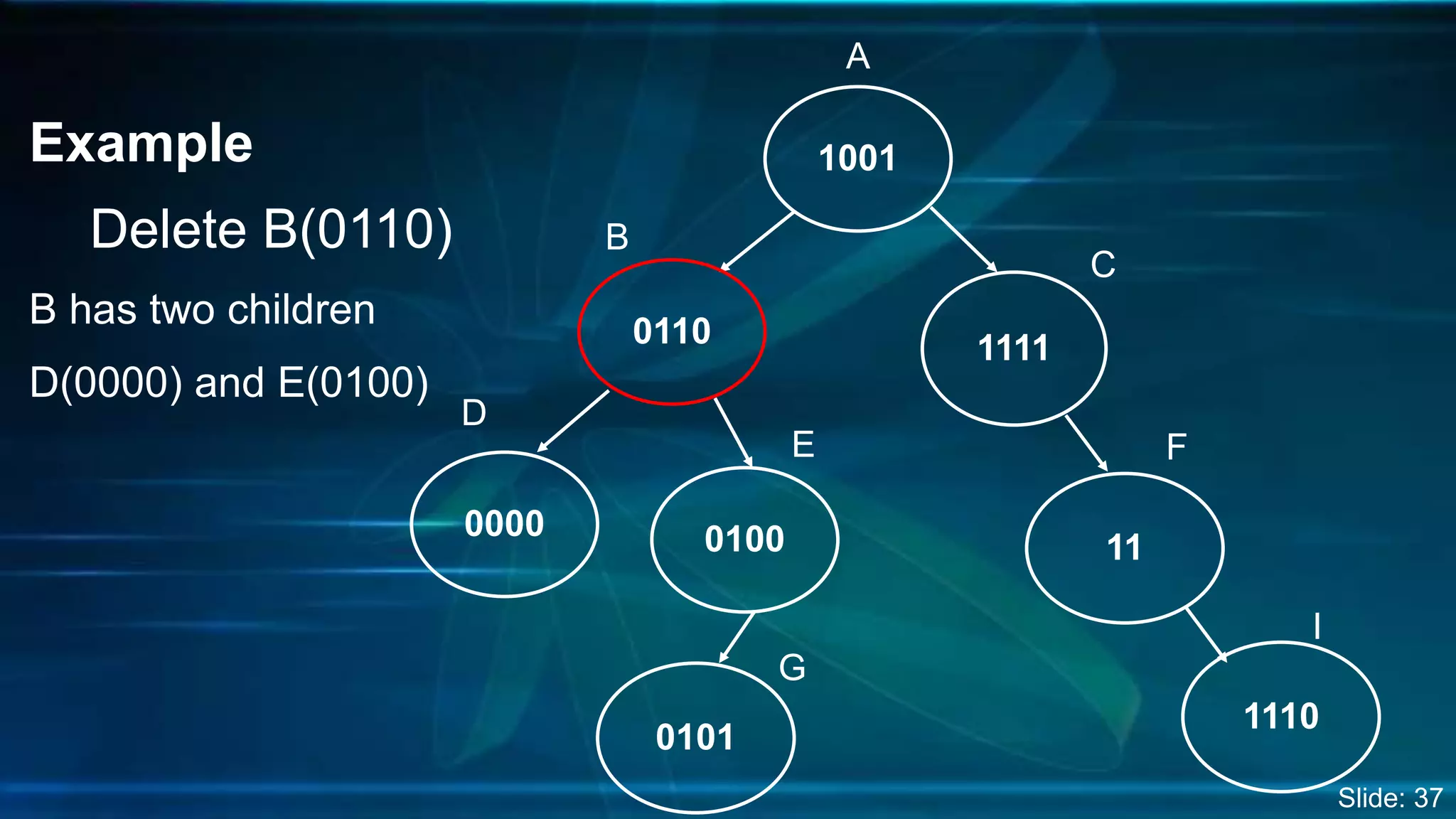
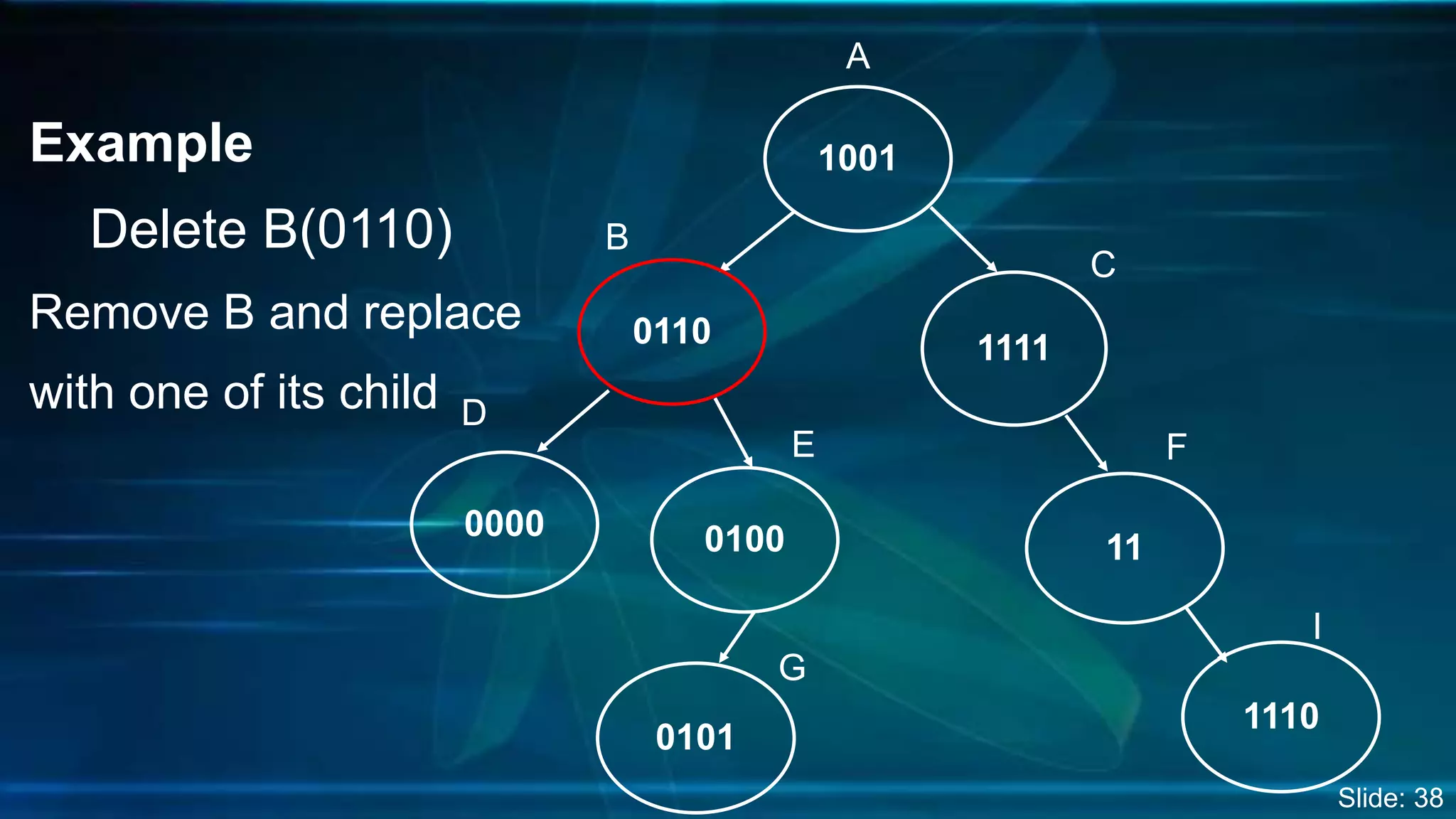
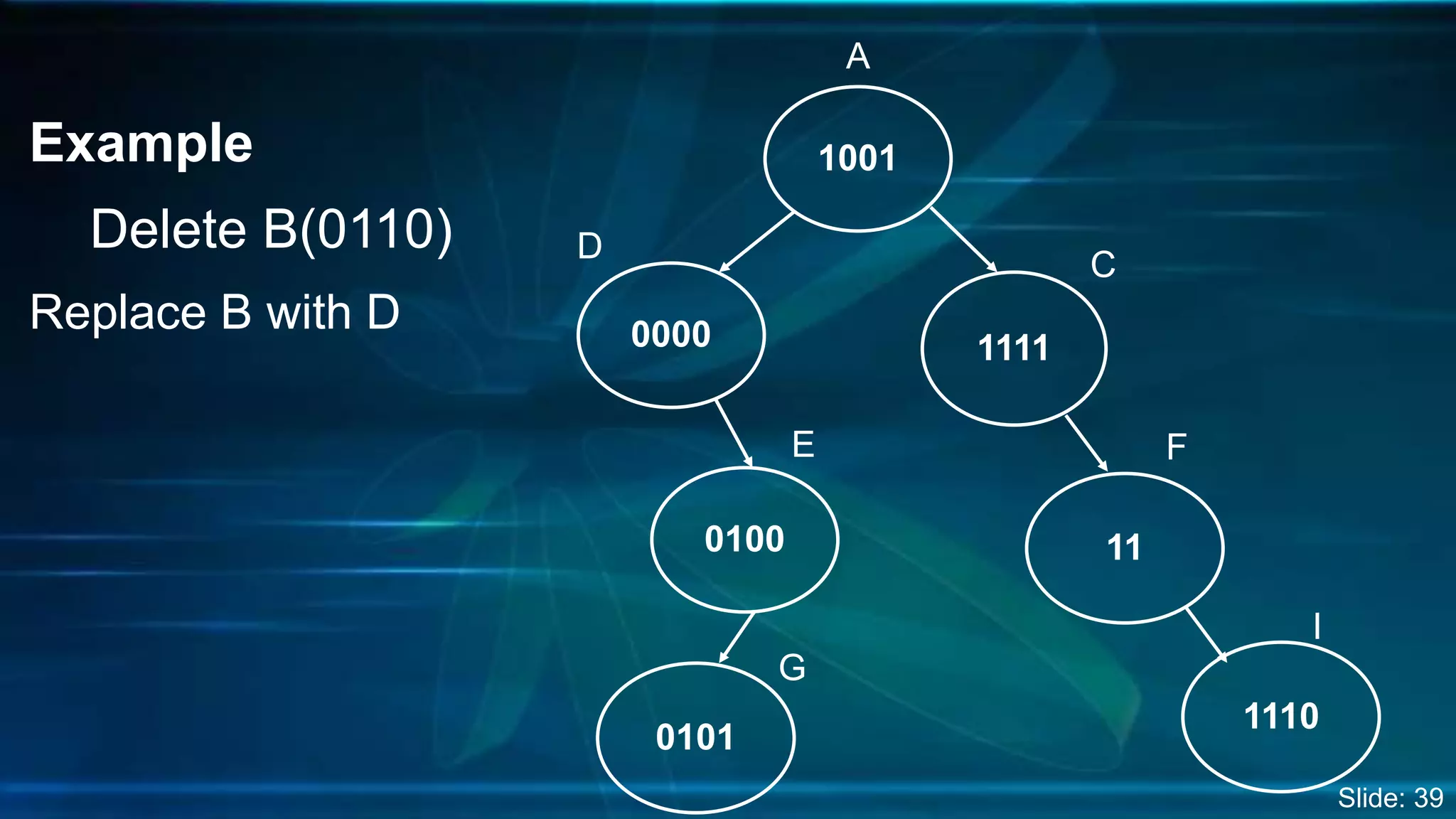
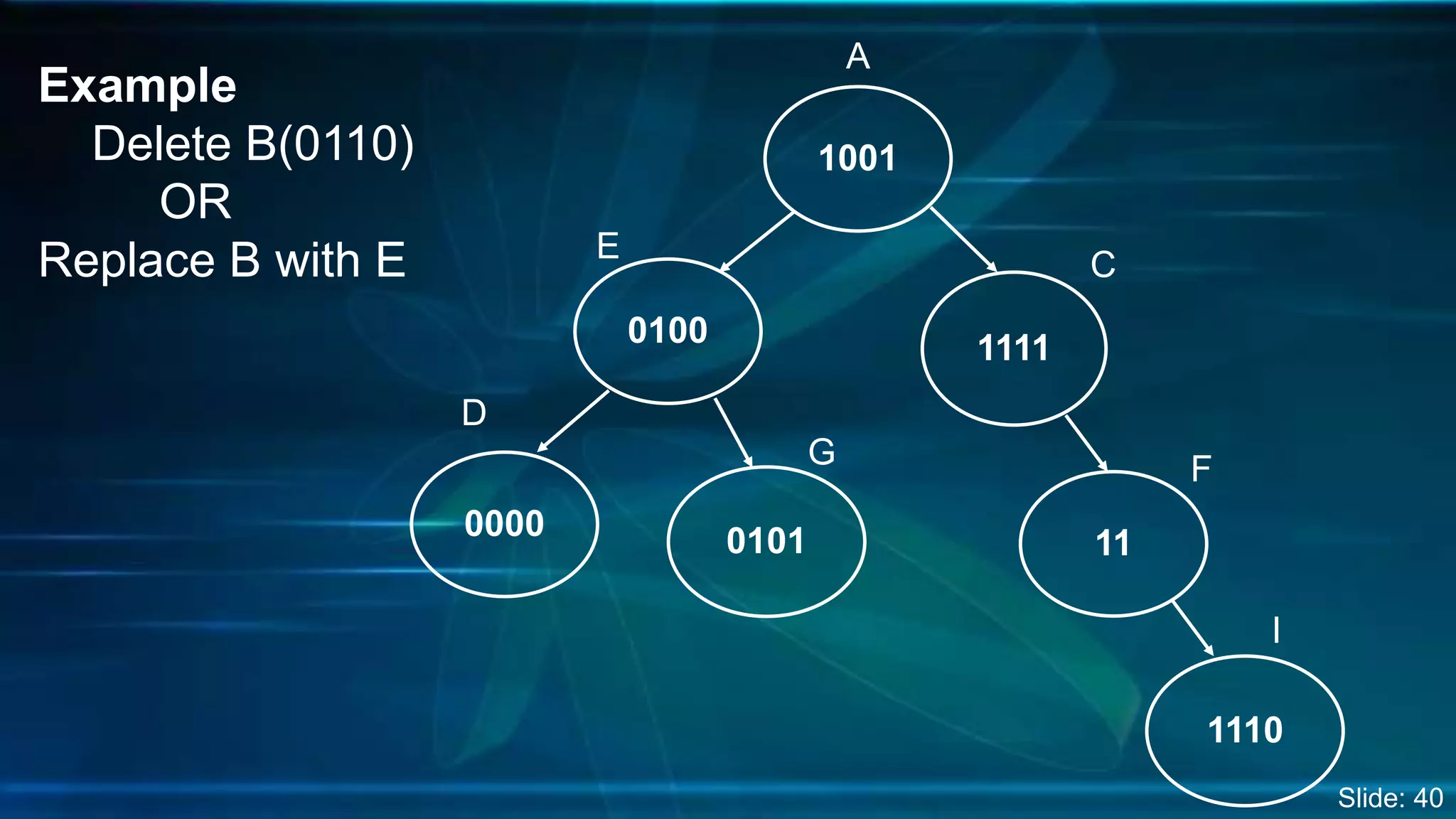
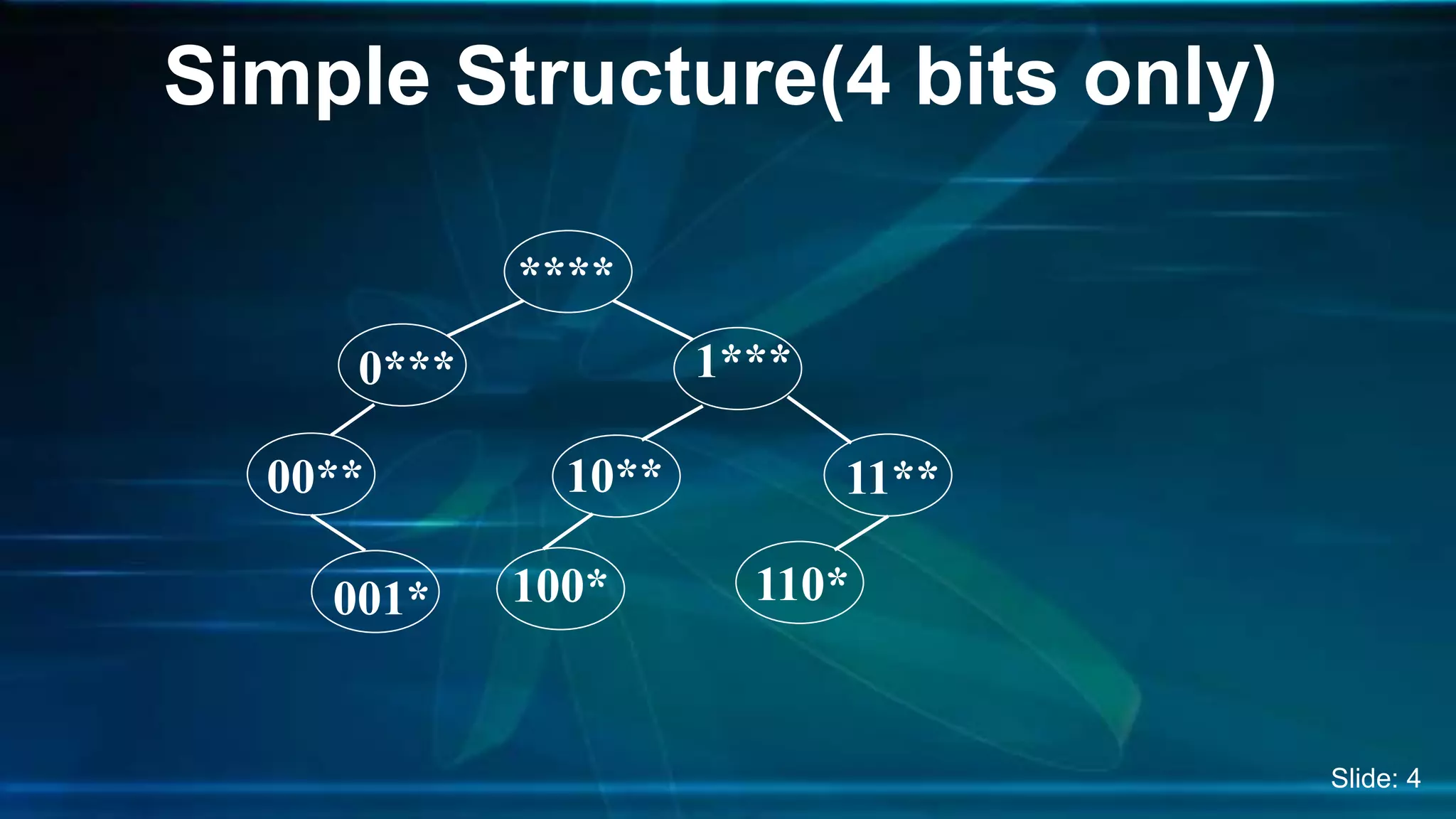
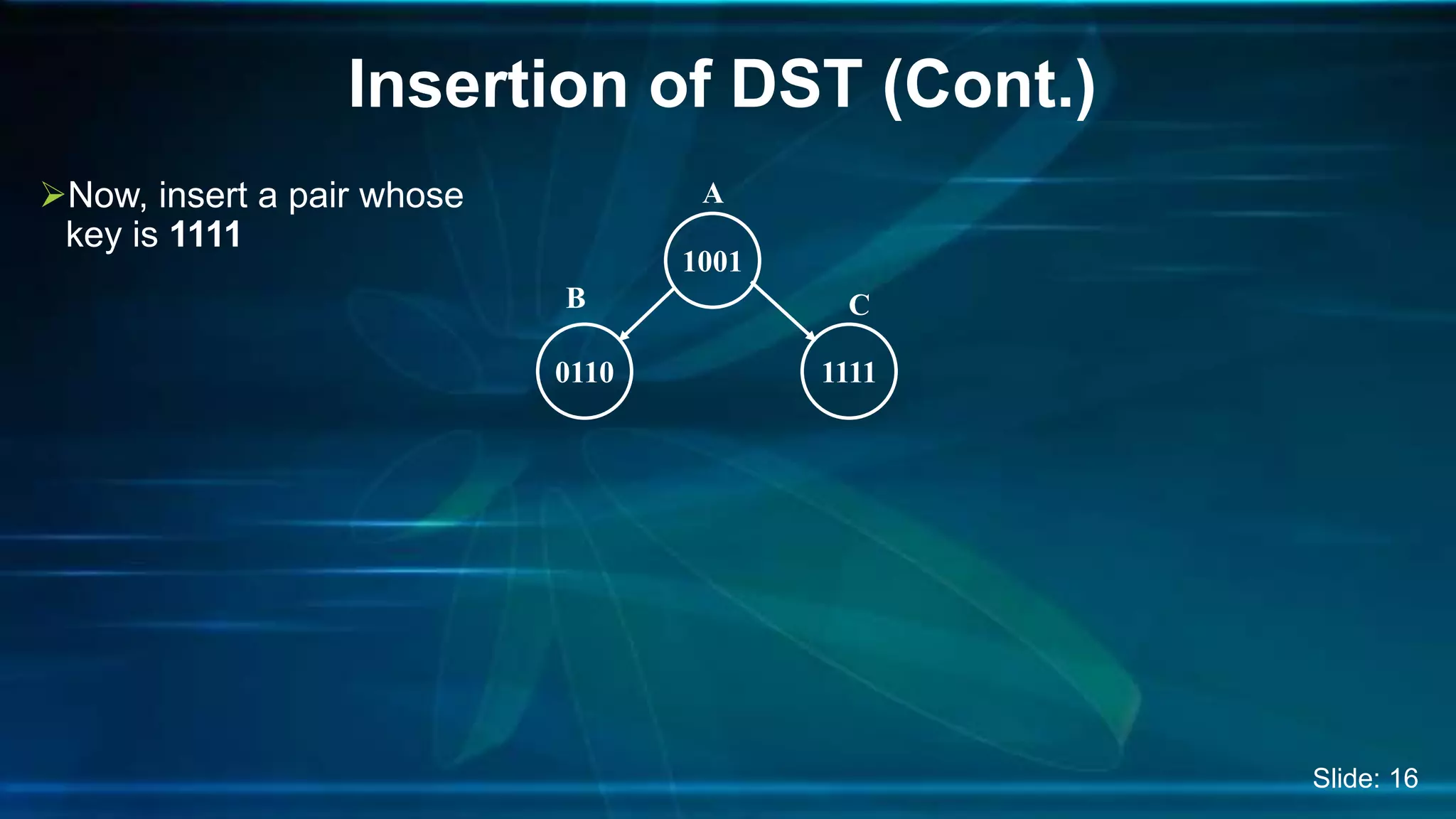
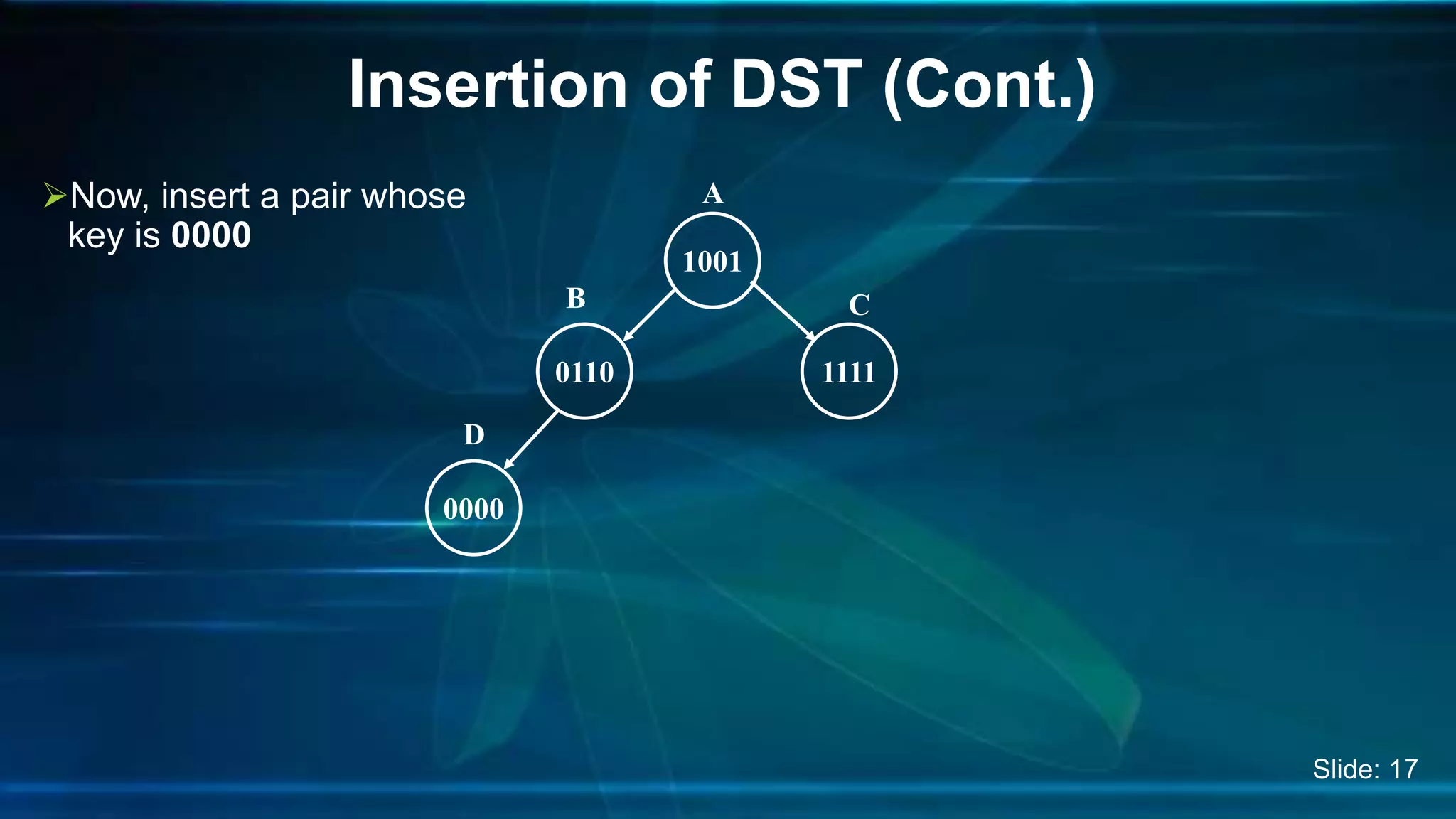
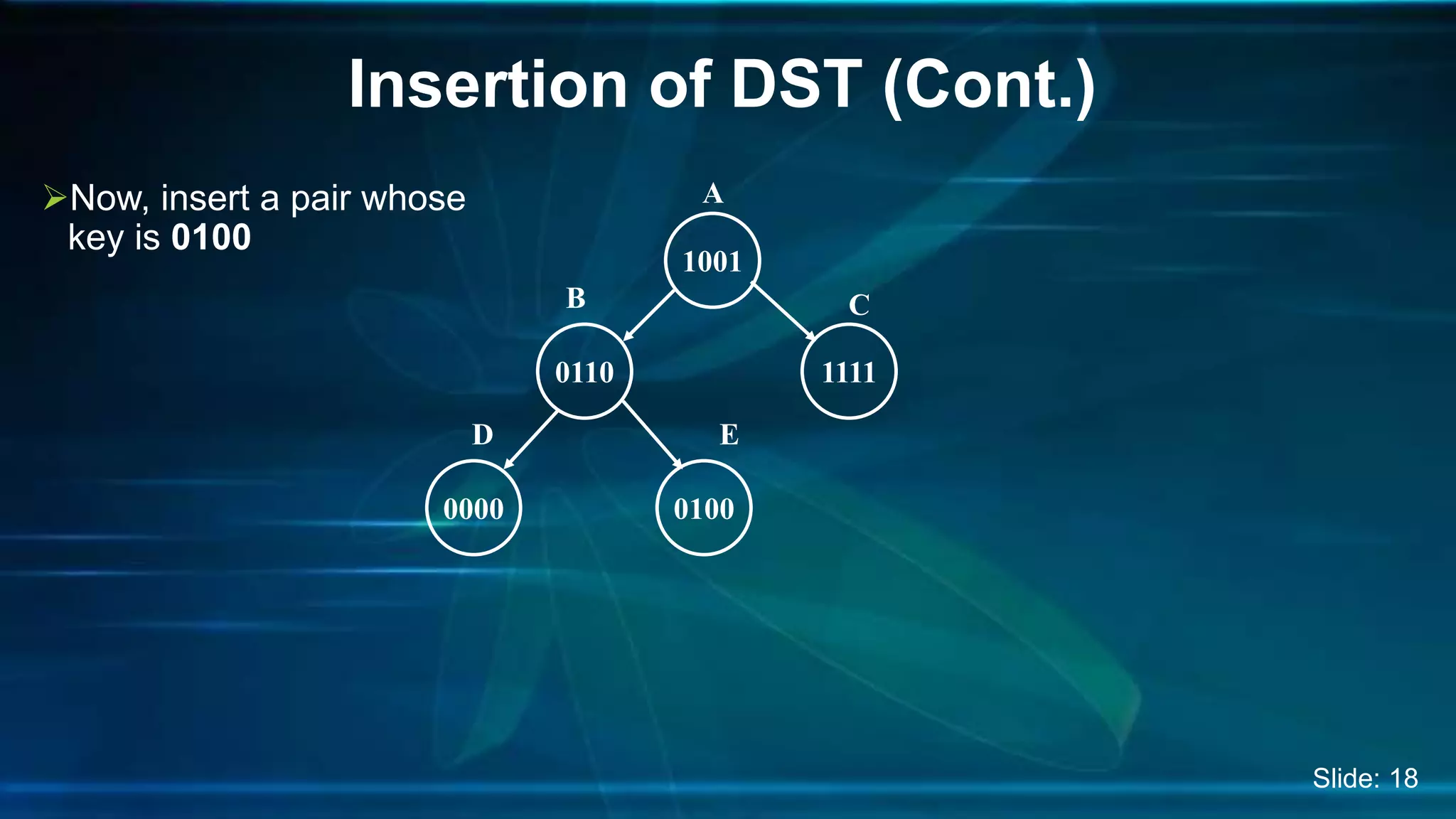
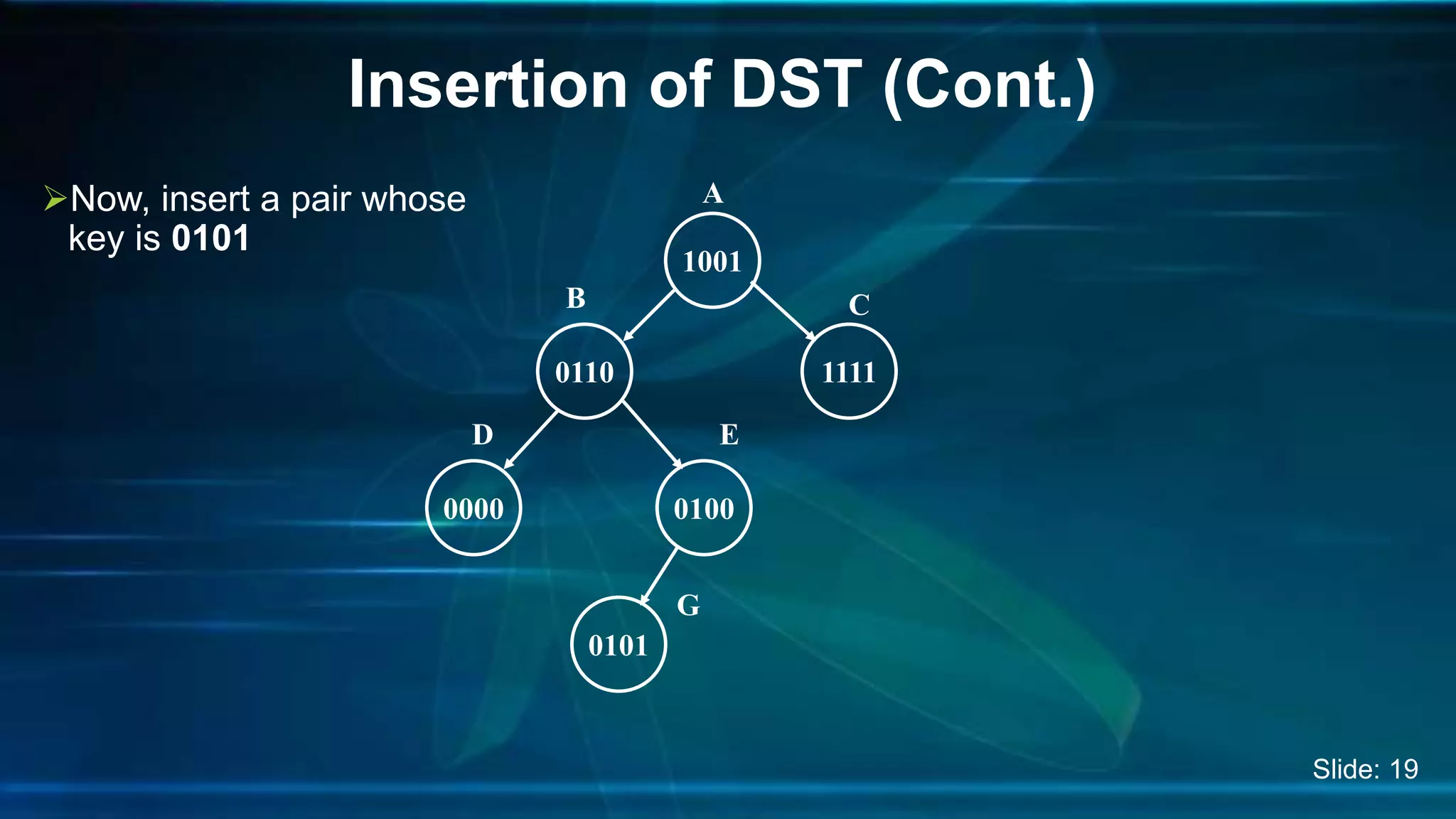
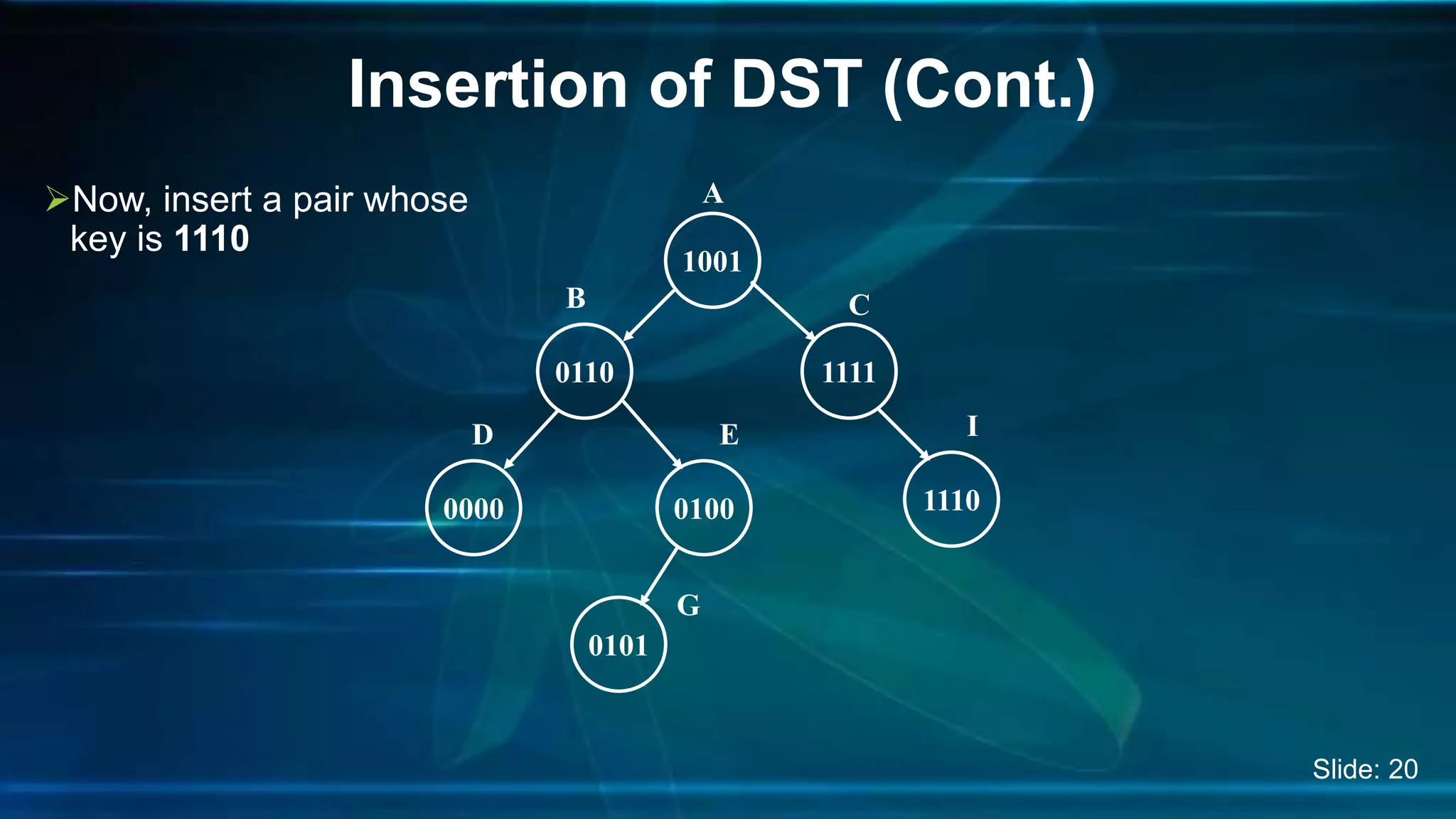
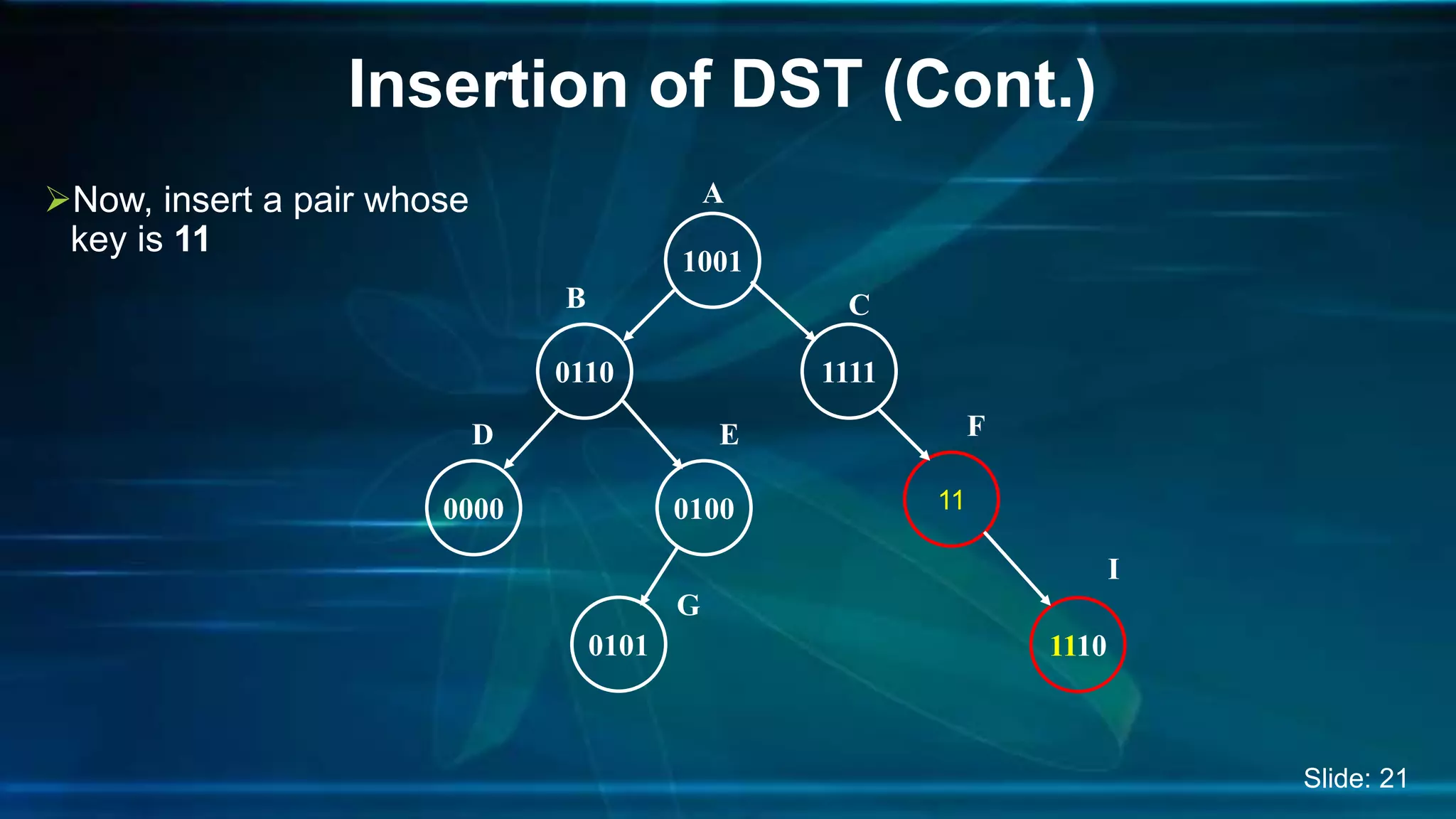
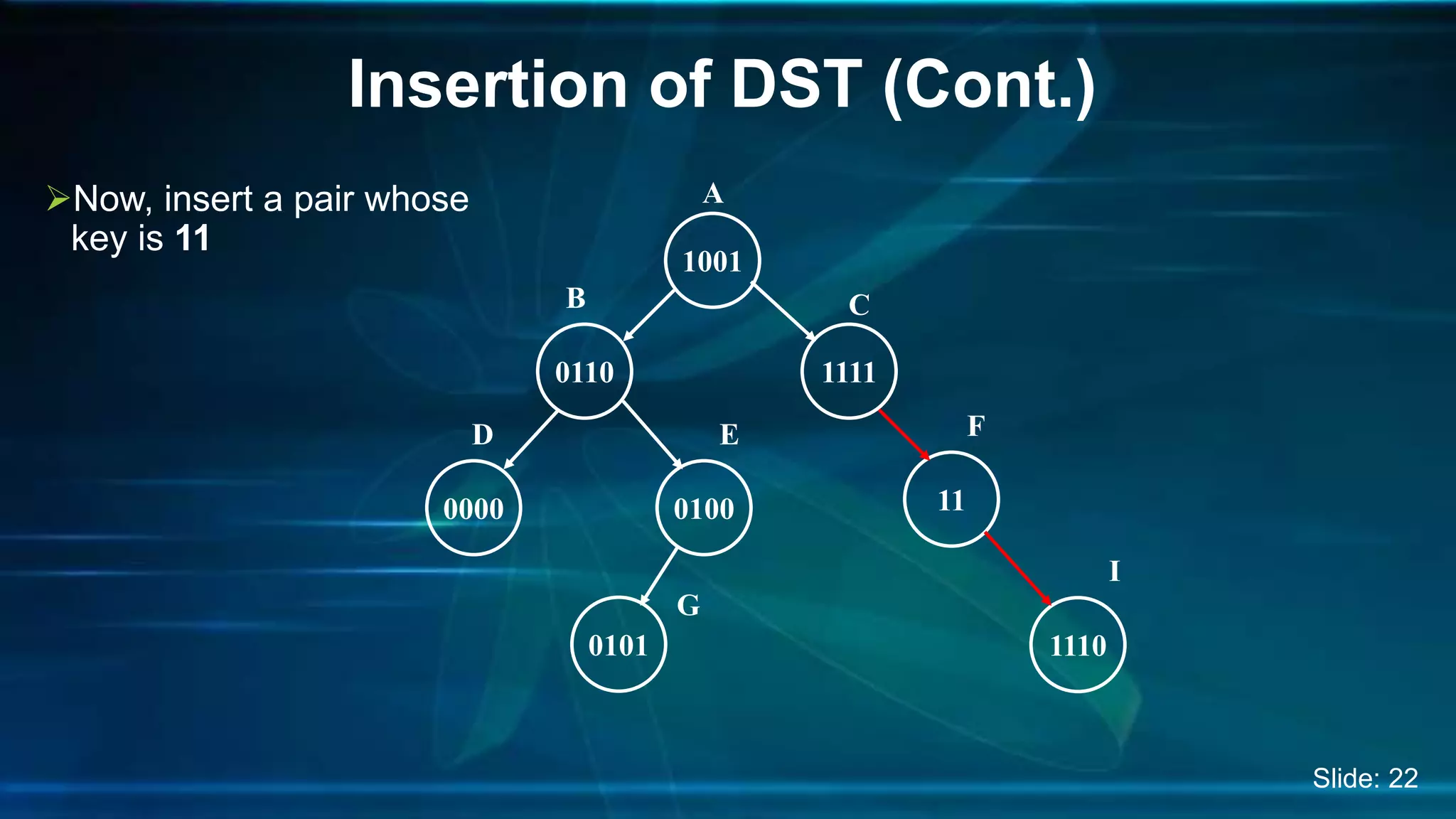
The document discusses Digital Search Trees (DST), a type of binary tree that efficiently handles binary data, describing their structure, insertion, search, and deletion operations. It highlights the benefits of DST over traditional binary search trees, including simplified operations and lower memory requirements, while also noting challenges such as handling duplicates and key length variations. Additionally, it covers applications like IP routing with IPv4 and IPv6, and network security with firewalls.

2. Nayeem Hasan
ID: 2013-1-60-066
S.M.Sadman Sadid
ID: 2013-1-60-065
Tanzim Rizwan
ID: 2013-1-60-063
Department of Computer Science & Engineering
East West University
Presented By
Slide: 1

3. Definition.
Structure.
Application.
Insertion.
Search.
Deletion.
OVERVIEW
Slide: 2

4. Definition
Digital search tree is one kind of binary tree which contains
only binary data.
If the bit of DST starts with 0 then it is in left subtree and if the
bit starts with 1 then it is in right subtree and this process works
recursively.
What is DST?
Slide: 3

5. Simple Structure(4 bits only)
****
0***
00**
001*
1***
10**
100*
11**
110*
Slide: 4

6. Digital Search Tree Example
A 00001
S 10011
E 00101
R 10010
C 00011
H 01000
A
S
R
E
C H
Slide: 5

7. Searching is based on binary representation of data.
If the data are randomly distributed then the average
search time per operation in O(log N), where N is the height of
the tree.
However, Worst case is O(b), where b is the number of bits
in the search key.
Search Time Of DST
Slide: 6

8. IP routing.
IPv4 – 32 bit IP address.
IPv6 – 128 bit IP address.
Firewalls.
Application Of DST
Slide: 7

9. IPv4 is the fourth generation of internet protocol version and the most
used version.
IPv4 uses 32 bit address which divided into four 8- bit parts and which
limits the address space to 4,294,967,296 (232 ) possible unique
address.
What is IPv4 and IPv6?
Slide: 8

10. IPv6 is the Internet's next-generation protocol and the current version of internet
protocol which replace the IPv4.
IPv6 uses 128- bit hexadecimal address which divides in 8 parts and each part
contains 16 bit binary number and which is designed to identification and location
system for computers on networks and routes traffic across the Internet.
Slide: 9

11. • A firewall is a network security system, either hardware or software based, that
controls incoming and outgoing network traffic based on a set of rules.
• Firewall is a software program or piece of hardware that helps screen out hackers,
viruses, and worms that try to reach your computer over the Internet
What is firewall?
Slide: 10

12. Insertion, search and deletion in DST are easier than the
Binary search tree and AVL tree.
This tree does not required additional information to
maintain the balance of the tree because the depth of the tree is
limited by the length of the key element.
DST requires less memory than Binary search tree and AVL
tree.
Benefit Of DST
Slide: 11

13. Bitwise operations are not always easy.
Handling duplicates is problematic.
Similar problem with keys of different lengths.
Data is not sorted.
If a key is long search and comparisons are costly, this can
be problem
Drawbacks Of DST
Slide: 12

14.  To insert an element in DST. There will be four(4) possible
cases.
 Tree Empty
 If found ‘0’, then go left
 If found ‘1’ then go right
 If found same key, then insert with prefix equal
Insertion of DST
Slide: 13

15. Insertion of DST (Cont.)
Start with an empty
digital search tree and
insert a pair whose key is
1001
1001
A
Slide: 14

16. Insertion of DST (Cont.)
Start with an empty
digital search tree and
insert a pair whose key is
1001
1001
AStart with an empty
digital search tree and
insert a pair whose key is
1001
Now, insert a pair whose
key is 0110
A
1001
0110
B
Slide: 15

17. Insertion of DST (Cont.)
Now, insert a pair whose
key is 1111
A
1001
0110
B
1111
C
Slide: 16

18. Insertion of DST (Cont.)
Now, insert a pair whose
key is 0000
A
1001
0110
B
1111
C
0000
D
Slide: 17

19. Insertion of DST (Cont.)
Now, insert a pair whose
key is 0100
A
1001
0110
B
1111
C
0000 0100
D E
Slide: 18

20. Insertion of DST (Cont.)
Now, insert a pair whose
key is 0101
A
1001
0110
B
1111
C
0000 0100
0101
D E
G
Slide: 19

21. Insertion of DST (Cont.)
Now, insert a pair whose
key is 1110
A
1001
0110
B
1111
C
0000 0100
0101
D E
G
1110
I
Slide: 20

22. Insertion of DST (Cont.)
Now, insert a pair whose
key is 11
A
1001
0110
B
1111
C
0000 0100
0101
D E
G
11
F
1110
I
Slide: 21

23. Insertion of DST (Cont.)
Now, insert a pair whose
key is 11
A
1001
0110
B
1111
C
0000 0100
0101
D E
G
11
F
I
1110
Slide: 22

24. Insertion Pseudo Code of DST
insert()
To insert an item, with a key, k, we begin a search from the root node to
locate the insertion position for the item.
 if t->root is null then
{
t->root = new node for the item with key k;
return null;
}
p = t->root;
i = max_b;
Slide: 23

25. loop
{
if p->key == k then a matching item has been found
return p->item;
i = i - 1; /*Traverse left or right branch, depending on the current bit.*/
let j be the value of the (i)th bit of k;
if p->a[j] is null then
{
p->a[j] = new node for the item with key k;
return null;
}
p = p->a[j];
}
Insertion Pseudo Code of DST
Slide: 24

26. In the above pseudo-code, insertion fails if there is already an item with key
k in the tree, and a pointer to the matching item will be returned.
Otherwise, when insertion is successful, a null pointer is returned. When the
new node, x, is created, its fields are initialized as follows.
x->key = k;
x->item = item;
x->a[0] = x->a[1] = NULL;
Insertion Pseudo Code of DST
Slide: 25

27. DST search for key K
For each node T in the tree we have 4 possible results
T is empty
K matches T
Current bit of K is a 0 and go to left child
Current bit of K is a 1 and go to right child
Search
Slide: 26

28. Example
Search 0001
NOT FOUND
1001
1111
11
0110
0000 0100
0101 1110
A
B
C
D
E
F
G
I
Slide: 27

29. Search 0000
Now 0000=D
So K found
1001
1111
11
0110
0000 0100
0101 1110
Example
A
B
C
D
E
F
G
I
Slide: 28

30. Search 1110
Now 1110=I
So K found
1001
1111
11
0110
0000 0100
0101 1110
Example
A
B
C
D
E
F
G
I
Slide: 29

31. Search 0100
Now 0100=E
So K found
1001
1111
11
0110
0000 0100
0101 1110
Example
A
B
C
D
E
F
G
I
Slide: 30

32. Struct node{
int key,info;
struct node *l,*r ;
}
static struct node *head,*z;
unsigned bits(unsigned x, int k, int j)
return (x>>k) & ~(~0<<j);
Int digital_search(int v)
{
struct node *x=head;
int b=maxb; // maxb is the number of bits in the key to be sorted
z->key=v;
while(v!=x->key)
x=(bits(v,b--,1) ? x->r : x->l;
return x->info;
}
C code of DST Search
Slide: 31

33. For each node T in the tree we have 3 possible cases.
 No child
 One child
 Two children
Delete
Slide: 32

34. Example
Delete G(0101)
1001
1111
11
0110
0000 0100
0101 1110
A
B
C
D
E
F
G
I
Slide: 33

35. Example
Delete G(0101)
G has no child,
So simply remove G
And replace
by a NIL pointer
1001
1111
11
0110
0000 0100
0101 1110
A
B
C
D
E
F
G
I
Slide: 34

36. Example
Delete F(11)
F has one child,
So, first remove F
1001
1111
11
0110
0000 0100
0101 1110
A
B
C
D
E
F
G
I
Slide: 35

37. Example
Delete F(11)
And link C with I
1001
11110110
0000 0100
0101
1110
A
B
C
D
E
G
I
Slide: 36

38. Example
Delete B(0110)
B has two children
D(0000) and E(0100)
1001
11110110
0000 0100
0101
11
A
B
C
D
E
G
F
1110
I
Slide: 37

39. Example
Delete B(0110)
Remove B and replace
with one of its child
1001
11110110
0000 0100
0101
11
A
B
C
D
E
G
F
1110
I
Slide: 38

40. Example
Delete B(0110)
Replace B with D
1001
11110000
0100
0101
11
A
C
D
E
G
F
1110
I
Slide: 39

41. 1001
1111
11
0000
0100
0101
1110
A
C
D
E
FG
I
Example
Delete B(0110)
OR
Replace B with E
Slide: 40

42. 1.Search key
2. if(key==Node)
free(Node);
if(Node->left==NULL && Node->right==NULL
Do Nothing;
else if(Node->left!=NULL)
Replace Node with next left Node
else if(Node->right!=NULL)
Replace Node with next right Node
else if(Node->right!=NULL && Node->left!=NULL )
Replace Node with next any Node
Delete Pseudo code of DST
Slide: 41

43. The digital search trees can be recommended for use whenever
the keys stored are integers
Character strings of fixed width.
DSTs are also suitable in many cases when the keys are strings
of variable length.
Conclusion
Slide: 42

44. THANK YOU ALL
Slide: 43