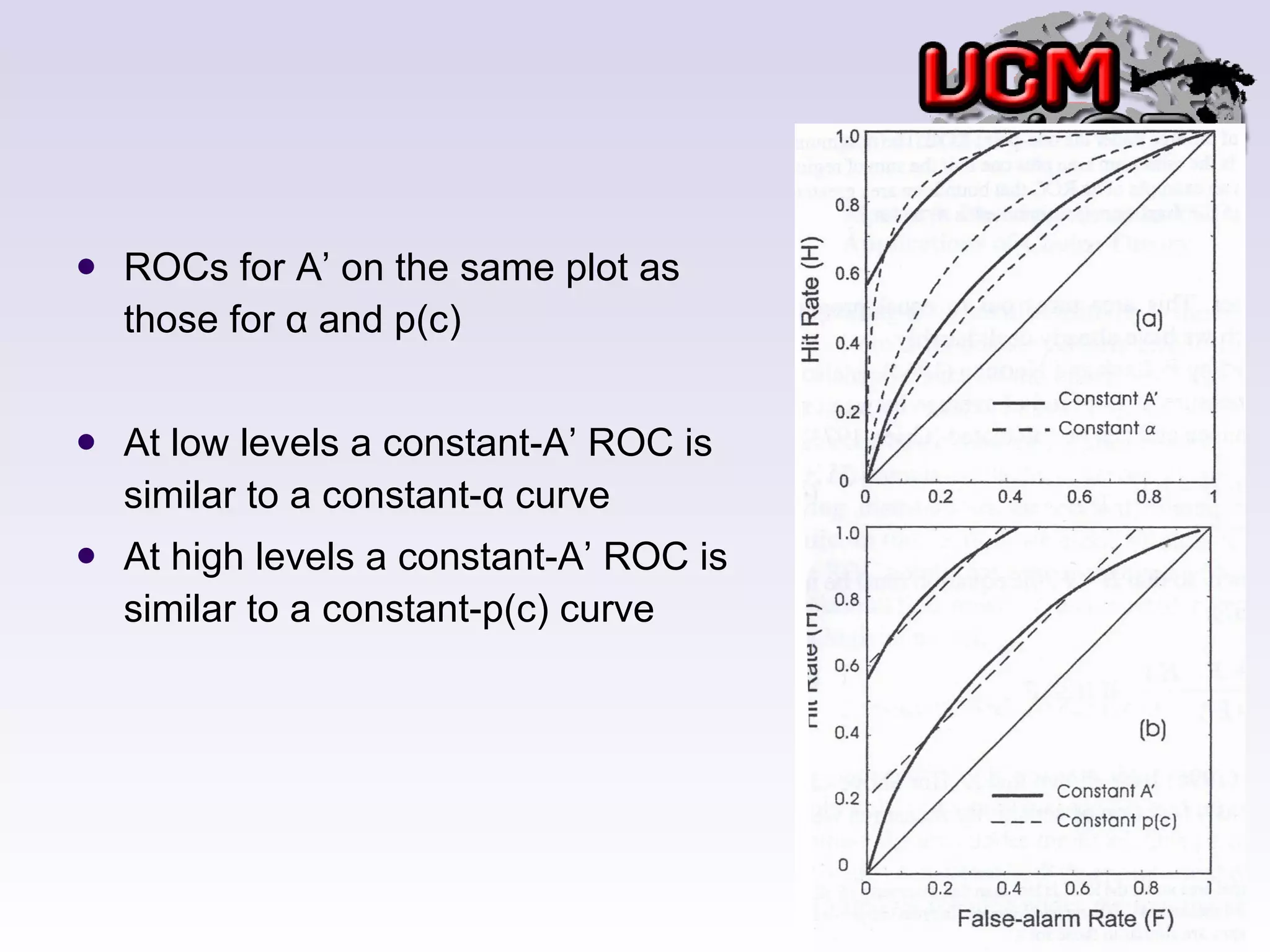
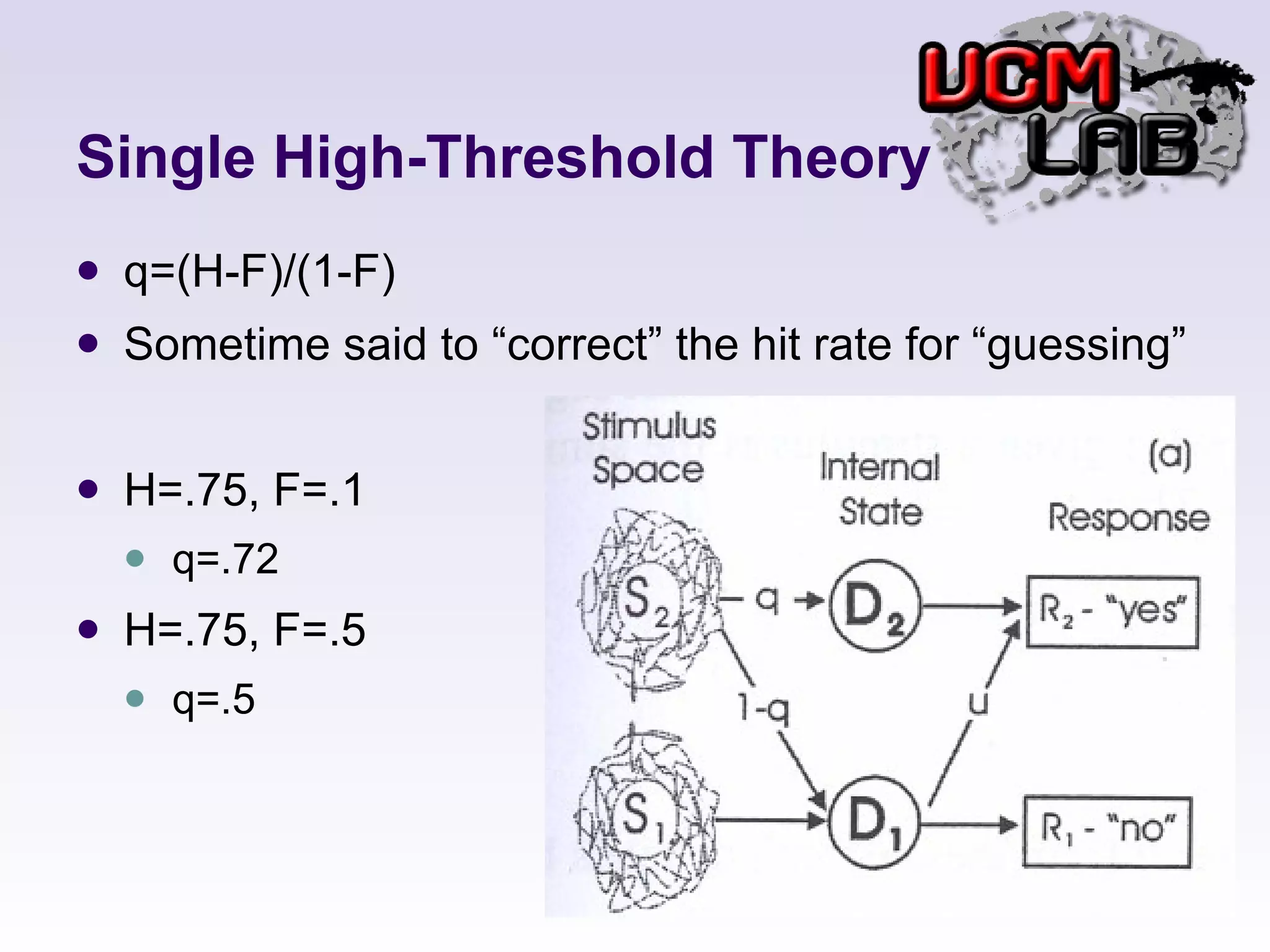
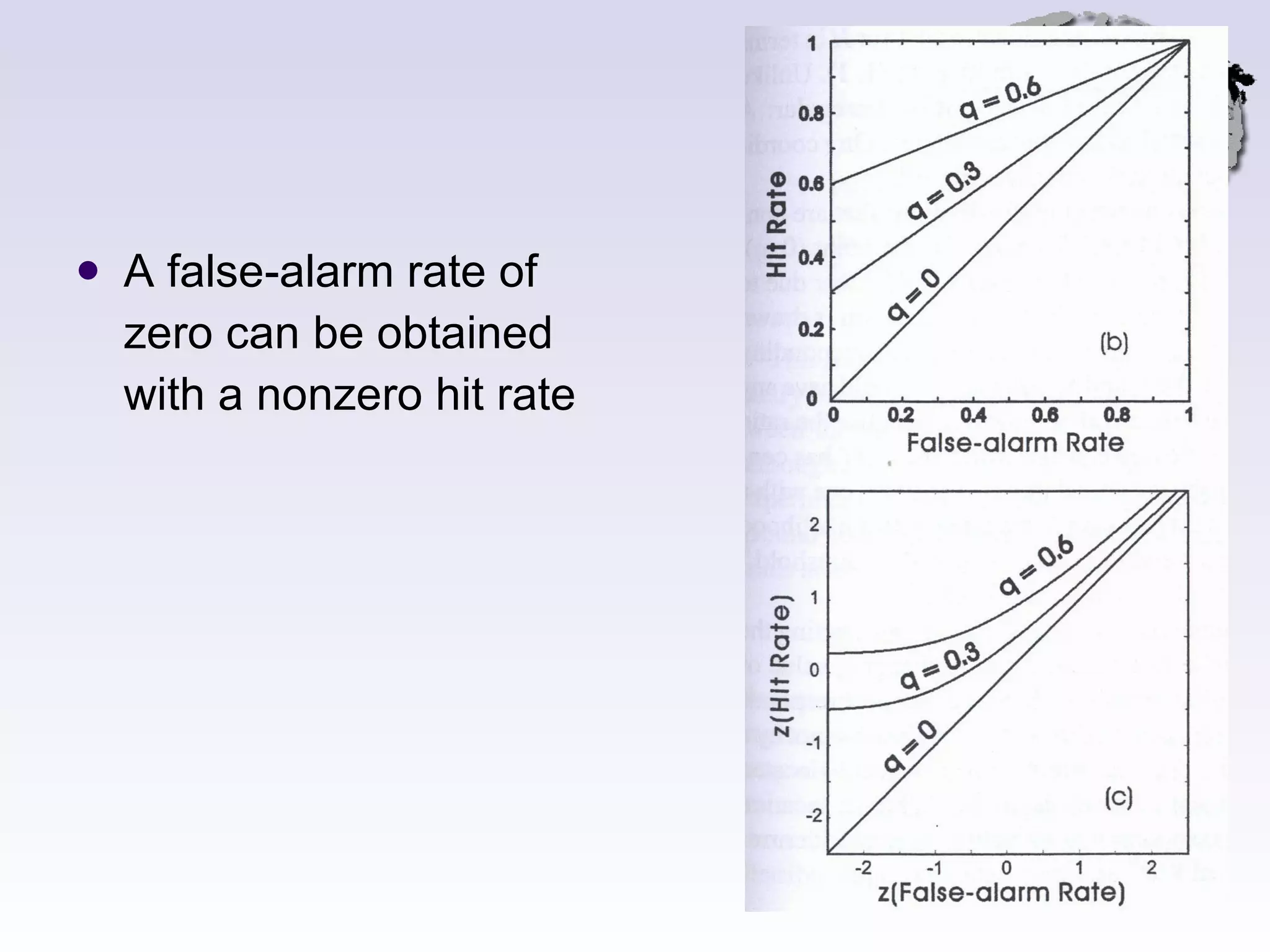
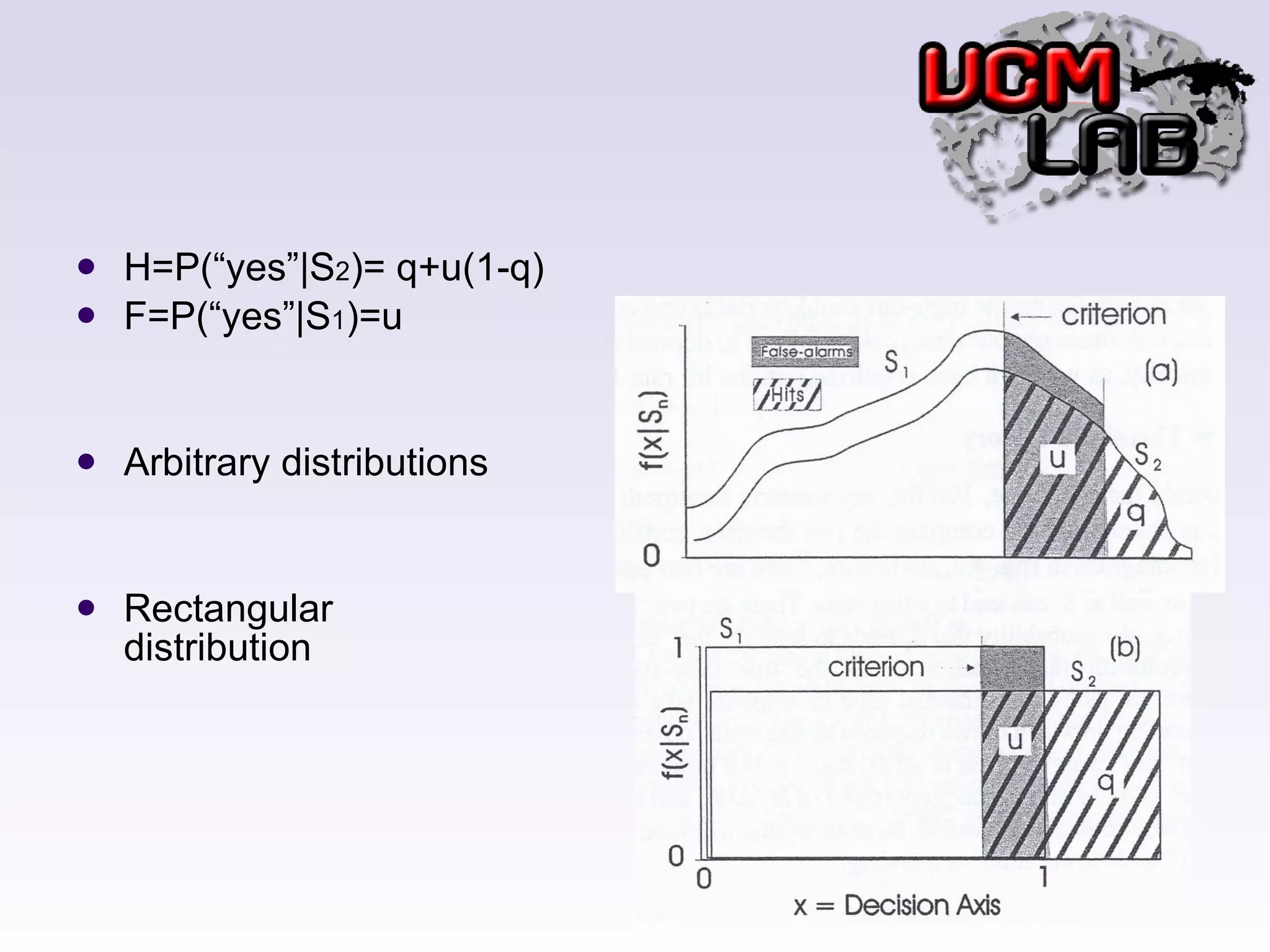
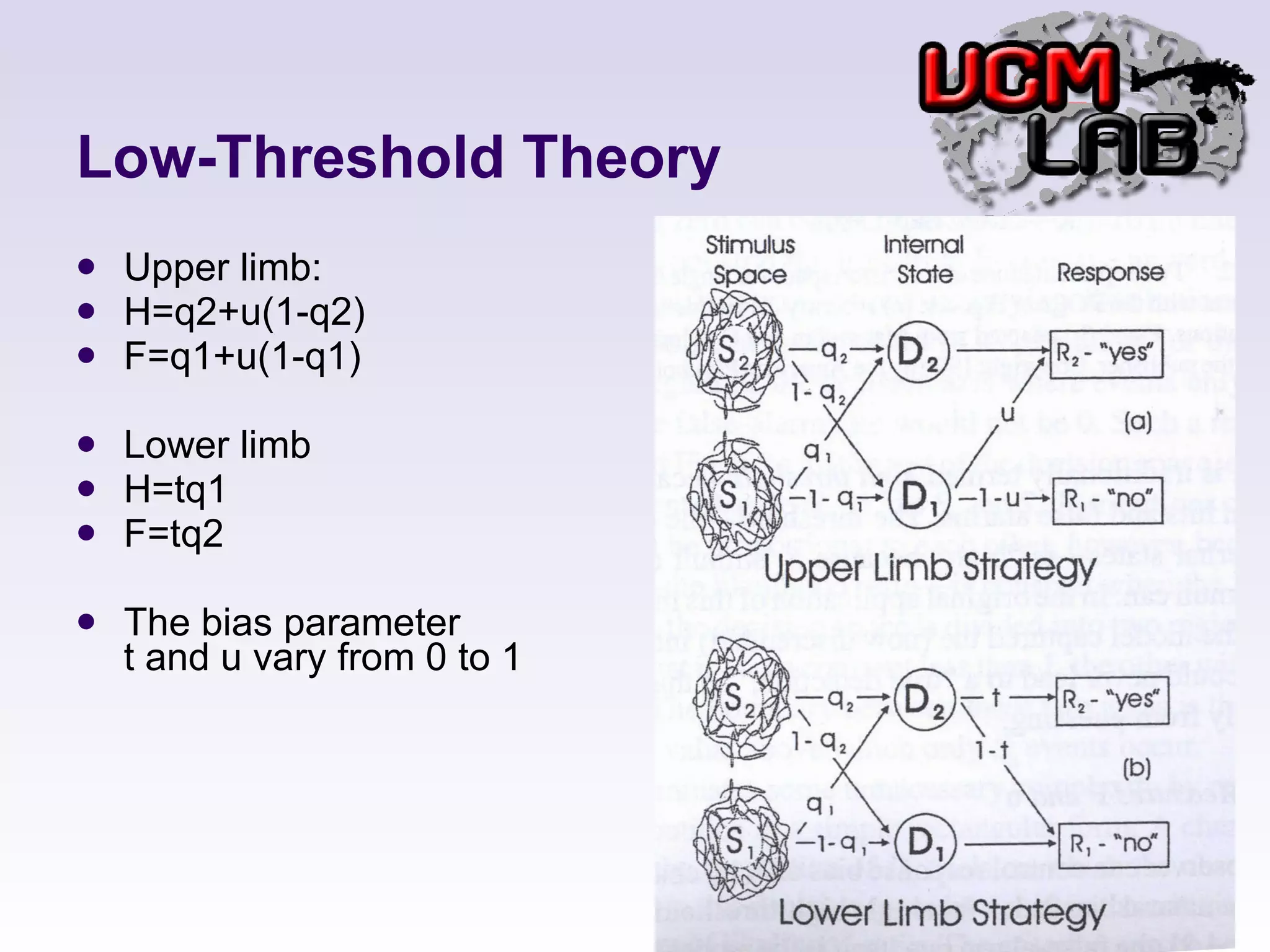
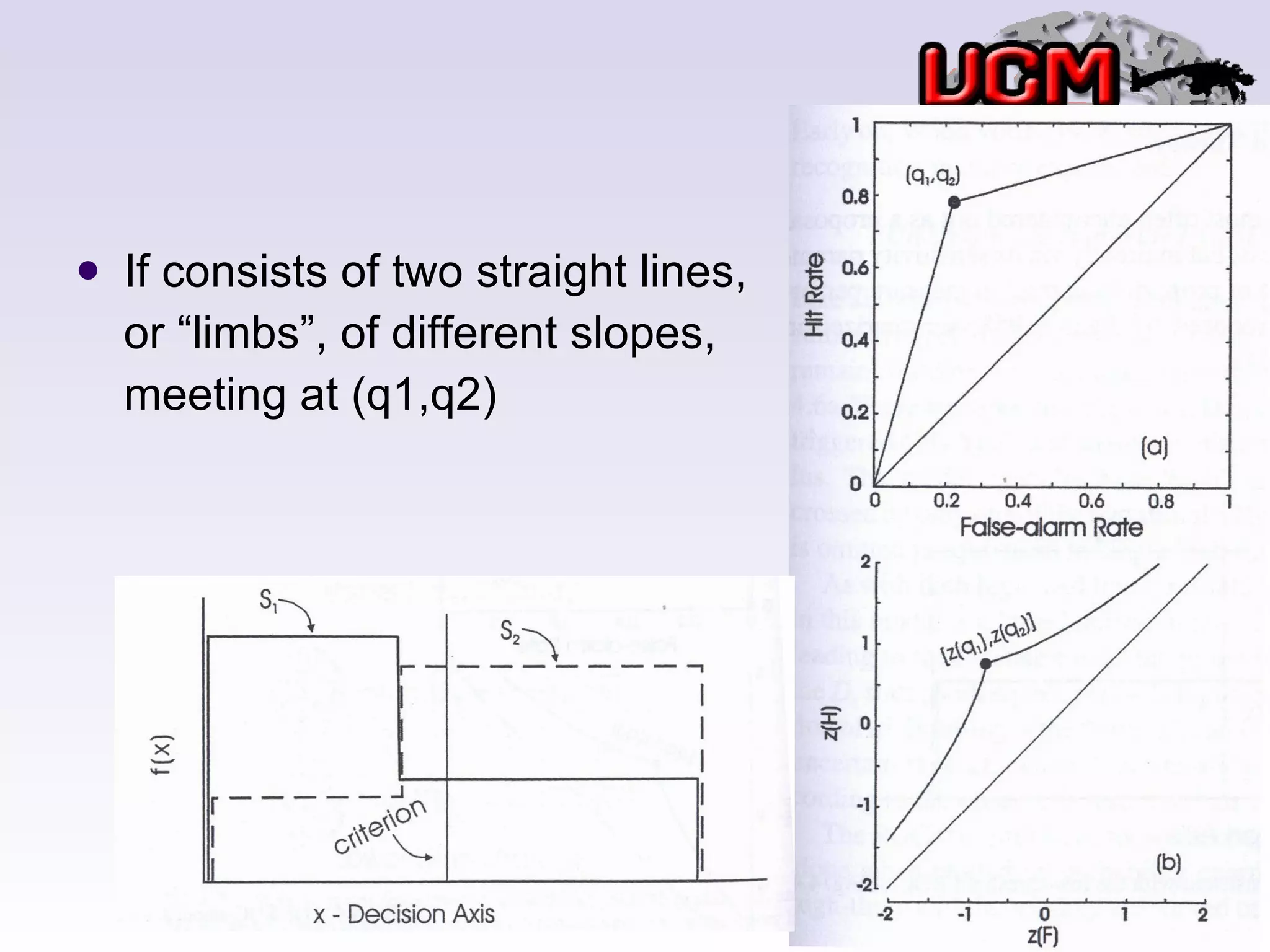
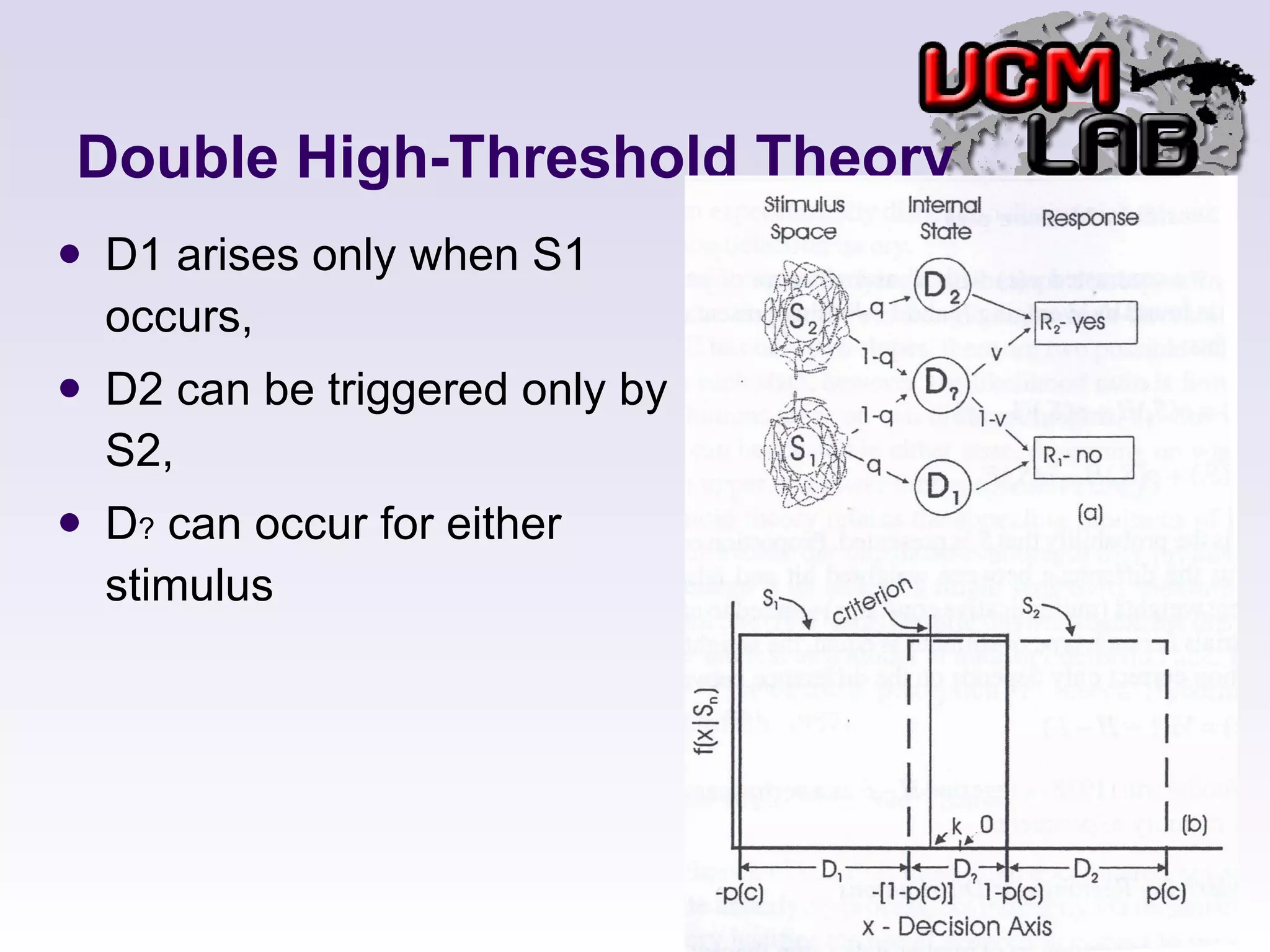
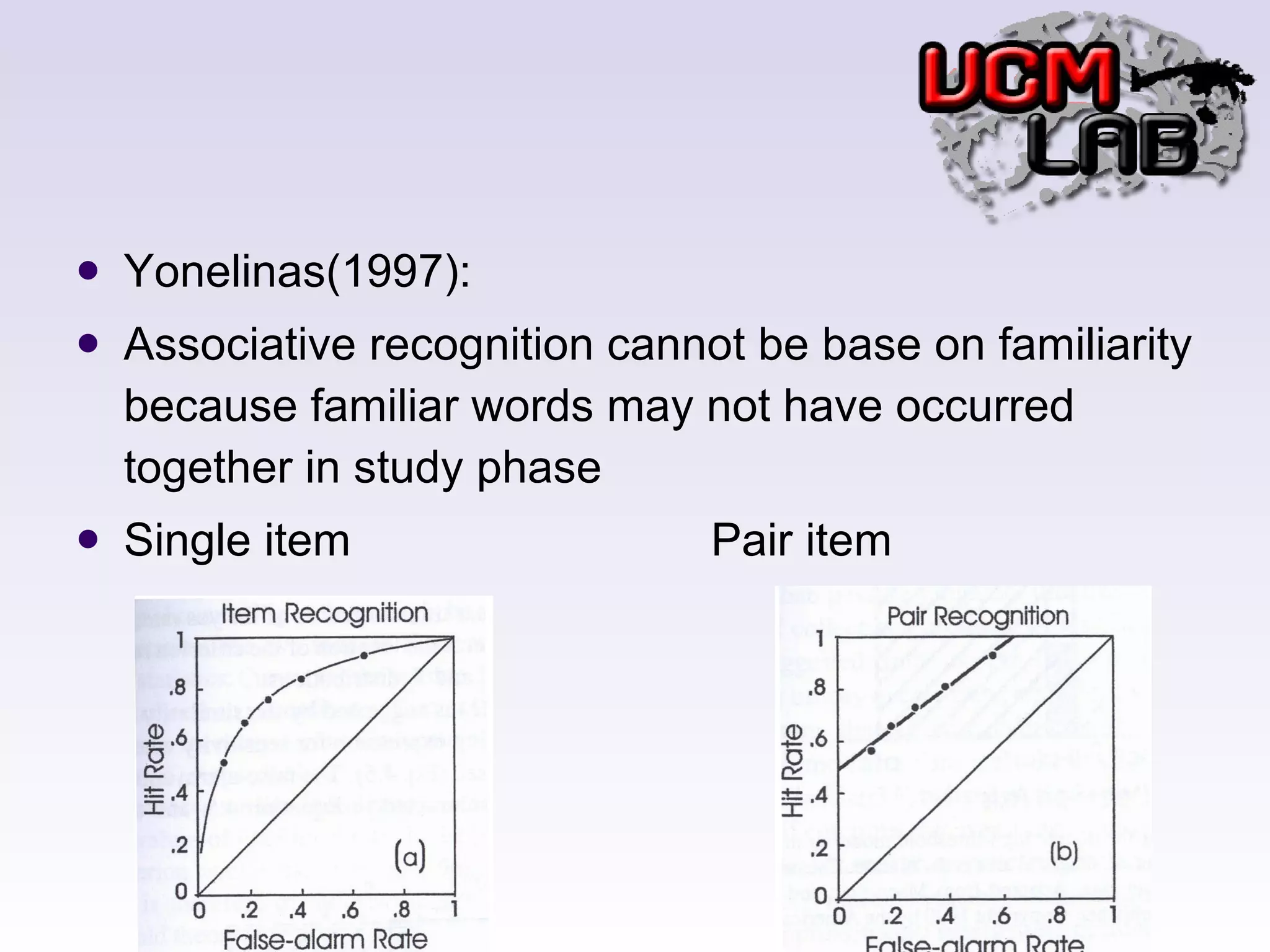
This document discusses several threshold and choice theories that were developed to model human decision making in psychophysics experiments. It describes single high-threshold theory, low-threshold theory, and double high-threshold theory, which make different assumptions about the thresholds used to discriminate between stimuli. It also discusses Luce's choice theory, which is based on choice axioms and models decisions using log-odds. Choice theory represents sensitivity using a measure called alpha and bias using a measure called beta.

1. Alternative Approaches: Threshold Models and Choice Theory CHAPTER 4, Detection Theory: A User’s Guide

2. Much psychophysics was concerned with measuring “thresholds” 1950s-1960s, developing SDT Luce(1959) proposed Choice Theory

3. Single High-Threshold Theory q=(H-F)/(1-F) Sometime said to “correct” the hit rate for “guessing” H=.75, F=.1 q=.72 H=.75, F=.5 q=.5

4. A false-alarm rate of zero can be obtained with a nonzero hit rate

5. H=P(“yes”|S 2 )= q+u(1-q) F=P(“yes”|S 1 )=u Arbitrary distributions Rectangular distribution

6. H=P(“yes”|S 2 )= q+u(1-q) F=P(“yes”|S 1 )=u 導回 q=(H-F)/(1-F) H=q+F(1-q) H=q+F-Fq q=H-F/1-F

7. The threshold –the dividing line between the internal states– is “high” because S1 cannot hurdle it, although S2 can.

8. Low-Threshold Theory Upper limb: H=q2+u(1-q2) F=q1+u(1-q1) Lower limb H=tq1 F=tq2 The bias parameter t and u vary from 0 to 1

9. Upper limb: u=F-q 1 /1-q 1 截距： q 2 -q 1 /1-q 1 , 斜率： 1-q 2 /1-q 1 Lower limb: t=F/q 1 截距： 0 , 斜率： q 2 /q 1

10. If consists of two straight lines, or “limbs”, of different slopes, meeting at (q1,q2)

11. Double High-Threshold Theory The sensitive Measure: p(c) p(c) =p(S2)H+p(s1)(1-F) =p(S1)+p(s2)H-p(S1)F p(Si) is the probability that Si is present

12. When the number of trials for each type of stimulus is equal, the weight are same and proportion correct only depends on difference between H and F ： p(c)=1/2 (1+H-F)

13. Double High-Threshold Theory D1 arises only when S1 occurs, D2 can be triggered only by S2, D ? can occur for either stimulus

14. Yonelinas(1997): Associative recognition cannot be base on familiarity because familiar words may not have occurred together in study phase Single item Pair item

15. H=q1+(q+q1)v F=(1-q2)v, v=F/1-q2 H=q1+(1-q1)xF/1-q2 =F(1-q1/1-q2)+q1 截距 =q1 , 斜率 =1-q1/1-q2 當 q1=q2=q 截距 =q, 斜率 =1

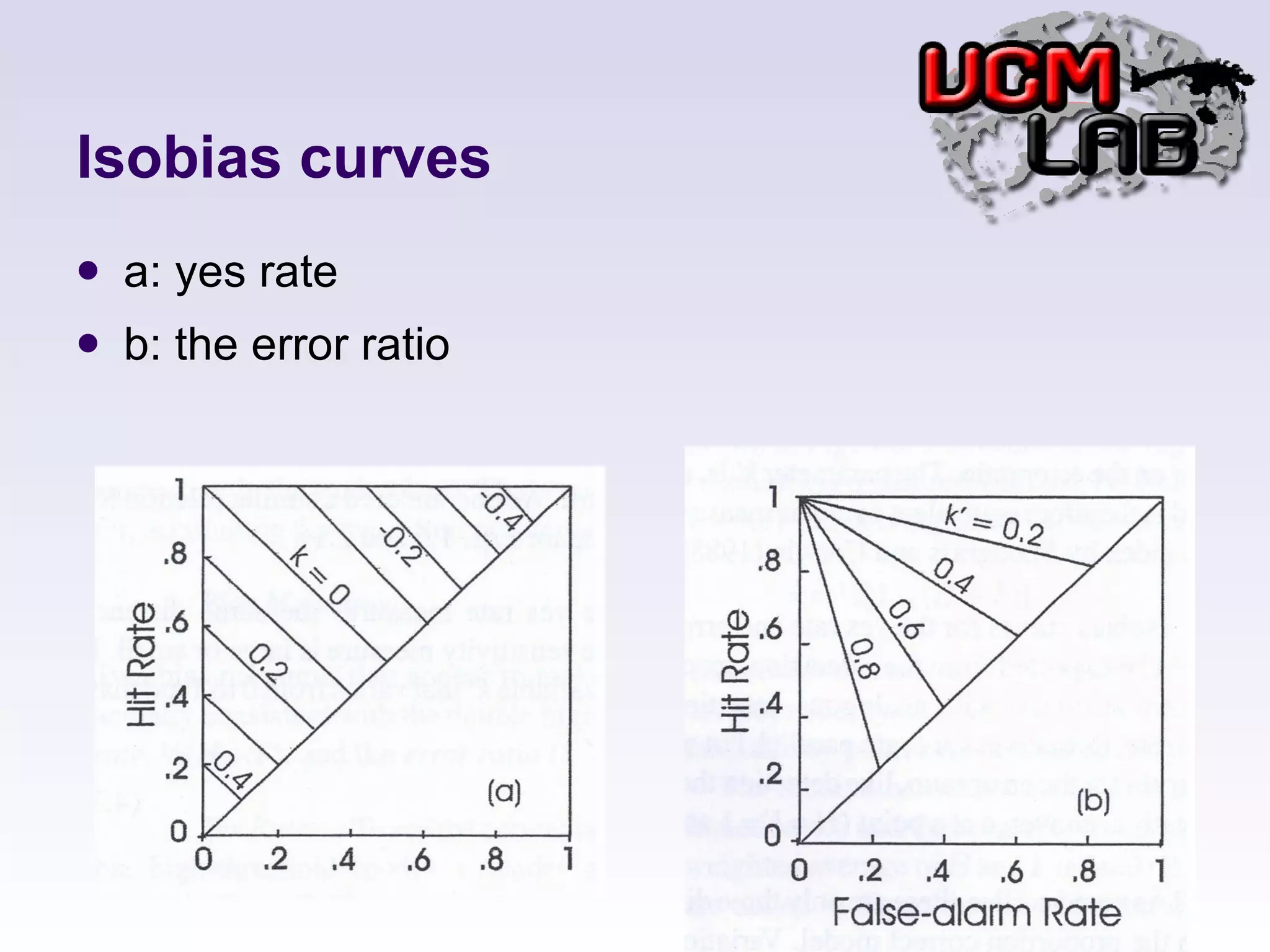
16. Yes Rate: ½ (H+F) Error Rate: (1-H)/F k is criterion H=p(c)-k F=1-p(c)-k k=1/2[1-(H+F)]

17. Error ratio: Linearly transform k into a new variable k’ that varies from 0 to 1, no matter what p(c) k’=[1+F/(1-H)] -1 k’=1-v

18. Isobias curves a: yes rate b: the error ratio

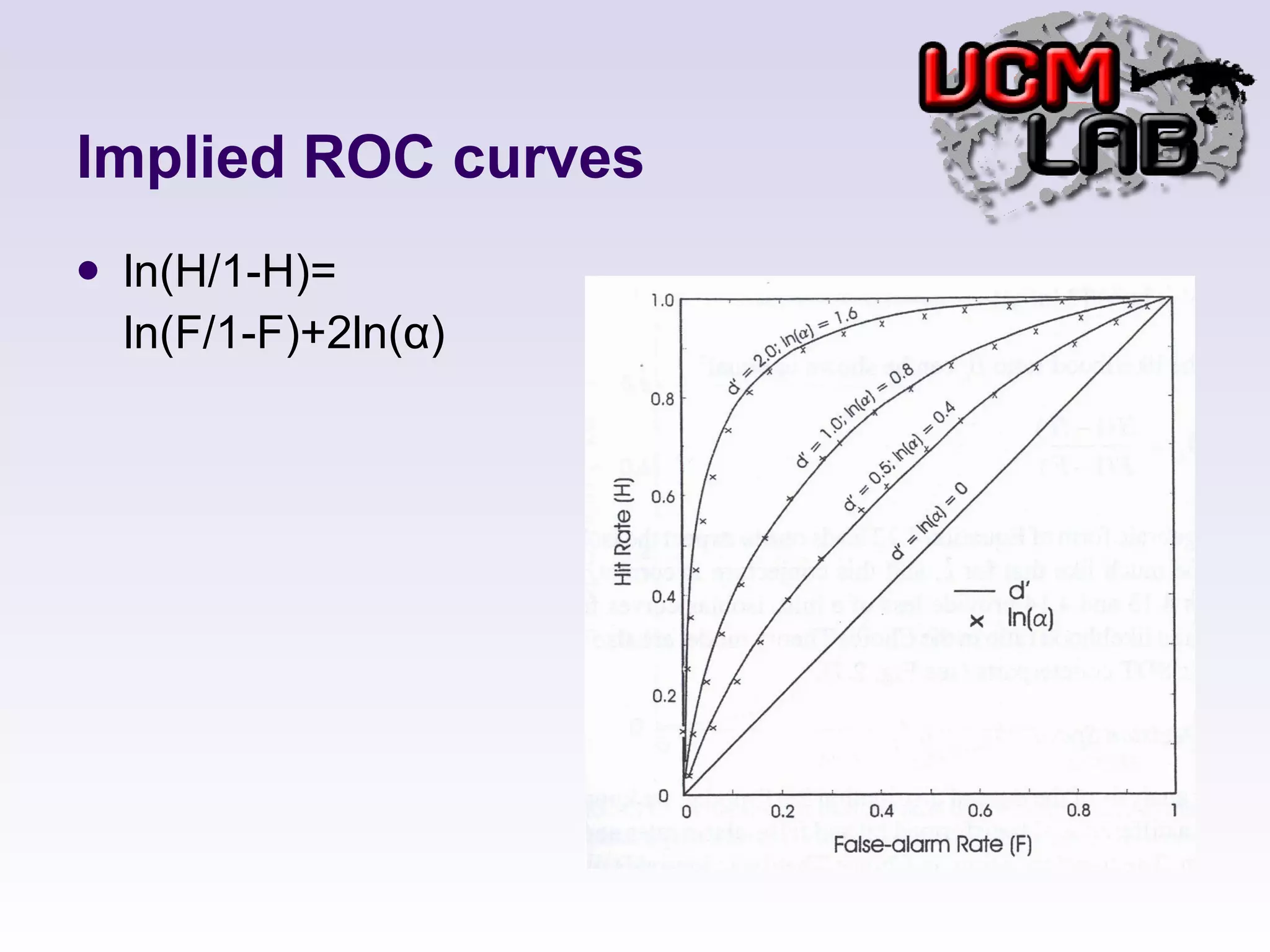
19. Choice Theory Base on choice axiom Sensitivity Measure: α α=[H(1-F)/(1-H)F] 1/2 ln(α)=1/2ln(H/1-H)-1/2ln(F/1-F)

20. Implied ROC curves ln(H/1-H)= ln(F/1-F)+2ln(α)

21. Bias Measures b (for “bias”)=[(1-H)(1-F)/HF] 1/2 ln(b)=-1/2[ln(H/1-H)+ln(F/1-F)] b’=ln(b)/[2 ln(α)] β L =H(1-H)/F1-F

22. Choice Theory is log-odds, which converts a proportion p to ln[p/(1-p)]

23. The logistic distribution is symmetric and only subtly different in shape from the normal when plot on a log-odds axis Sensitivity measure: 2ln(α) Criterion: ln(b)

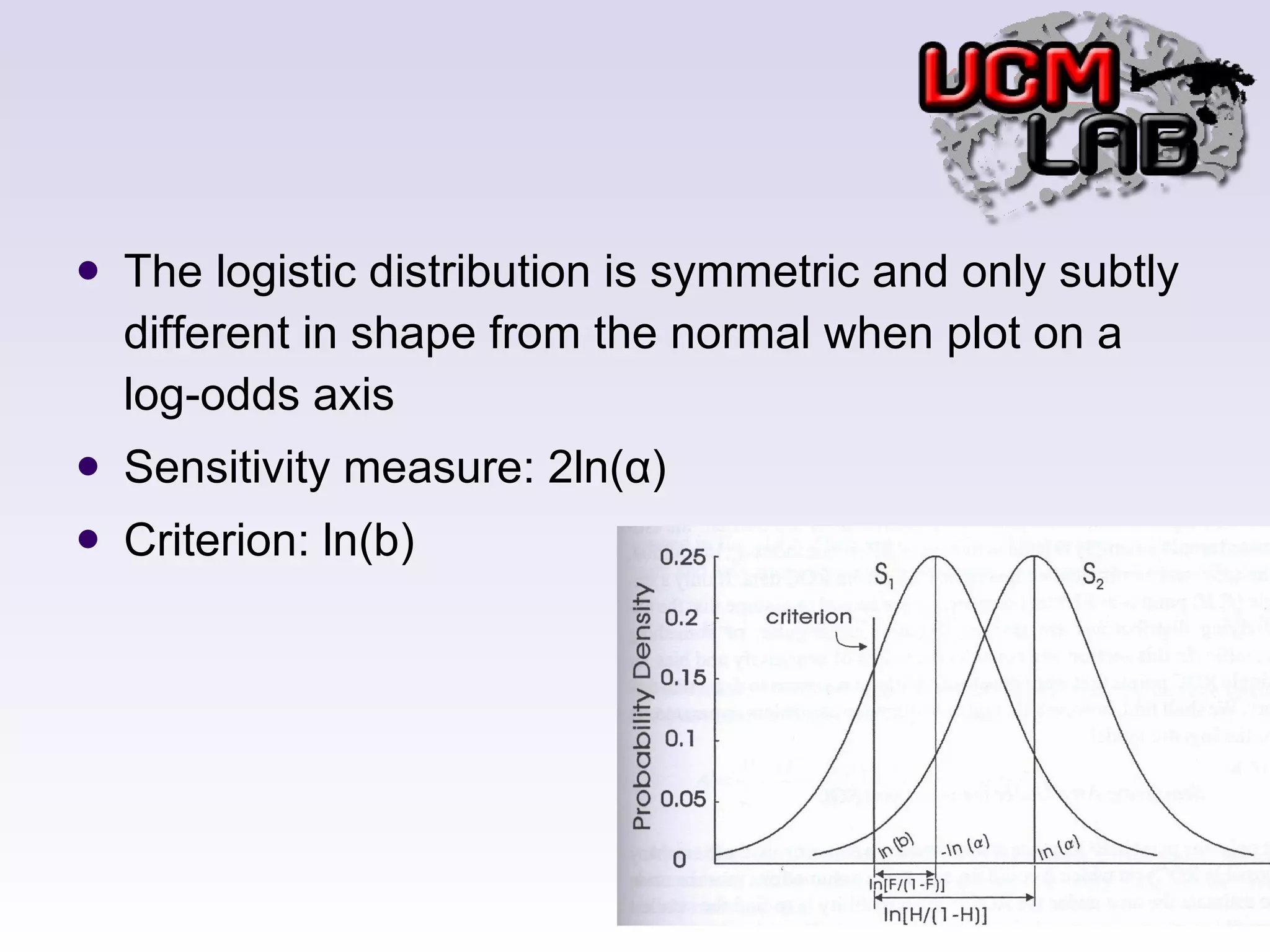
24. x= ln[p/(1-p)] p=1/(1+e x ) x must be expressed as a distance from the mean S2 distribution: x=ln(b)-ln(α) S1 distribution: x=ln(b)+ln(α) H=α/(α+b) F=1/(1+αb)

25. Unbiased observer, b=1 H=α/(α+1) F=1/(1+α) =>H=1-F p(c)=α/(α+1)

26. Area Under the one-point ROC A’=1/2+(H-F)(1+H-F)/4H(1-F), if H>=F A’= 1/2+(F-H)(1+F-H)/4F(1-H), if H<=F A’=1/2+1/2p(c){1-1/[2ln(α)] 2 }

27. ROCs for A’ on the same plot as those for α and p(c) At low levels a constant-A’ ROC is similar to a constant-α curve At high levels a constant-A’ ROC is similar to a constant-p(c) curve

28. Bias Measures Based on ROC Geometry B’’ must be modified if performance is below chance B’’=H(1-H)-F(1-F)/H(1-H)+F(1-F), if H>=F B’’=F(1-F)-H(1-H)/H(1-H)+F(1-F), if H<=F

29. Nonparametric Analysis of Rating Data Dual-response version of ratings paradigm 分別對 signal/noise 做信心評量， 並測量 FA 和 H 的差異可得 S’ S’ did a better job than d’ of rank ordering conditions that differed slightly in sensitivity

30. Essay: The Appeal of discrete Model Subliminal perception Classification of speech Sounds Statistical Hypothesis Testing