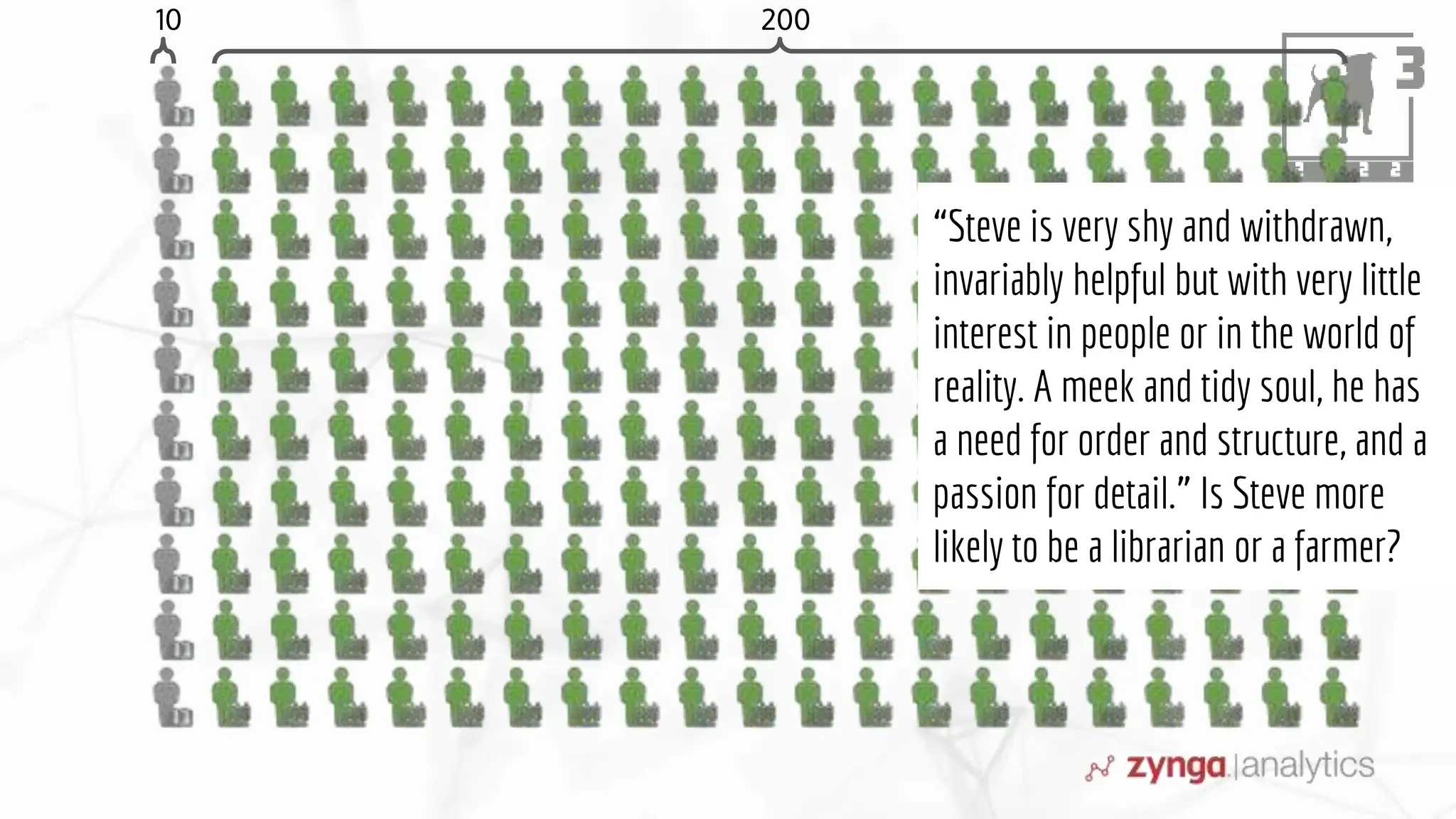
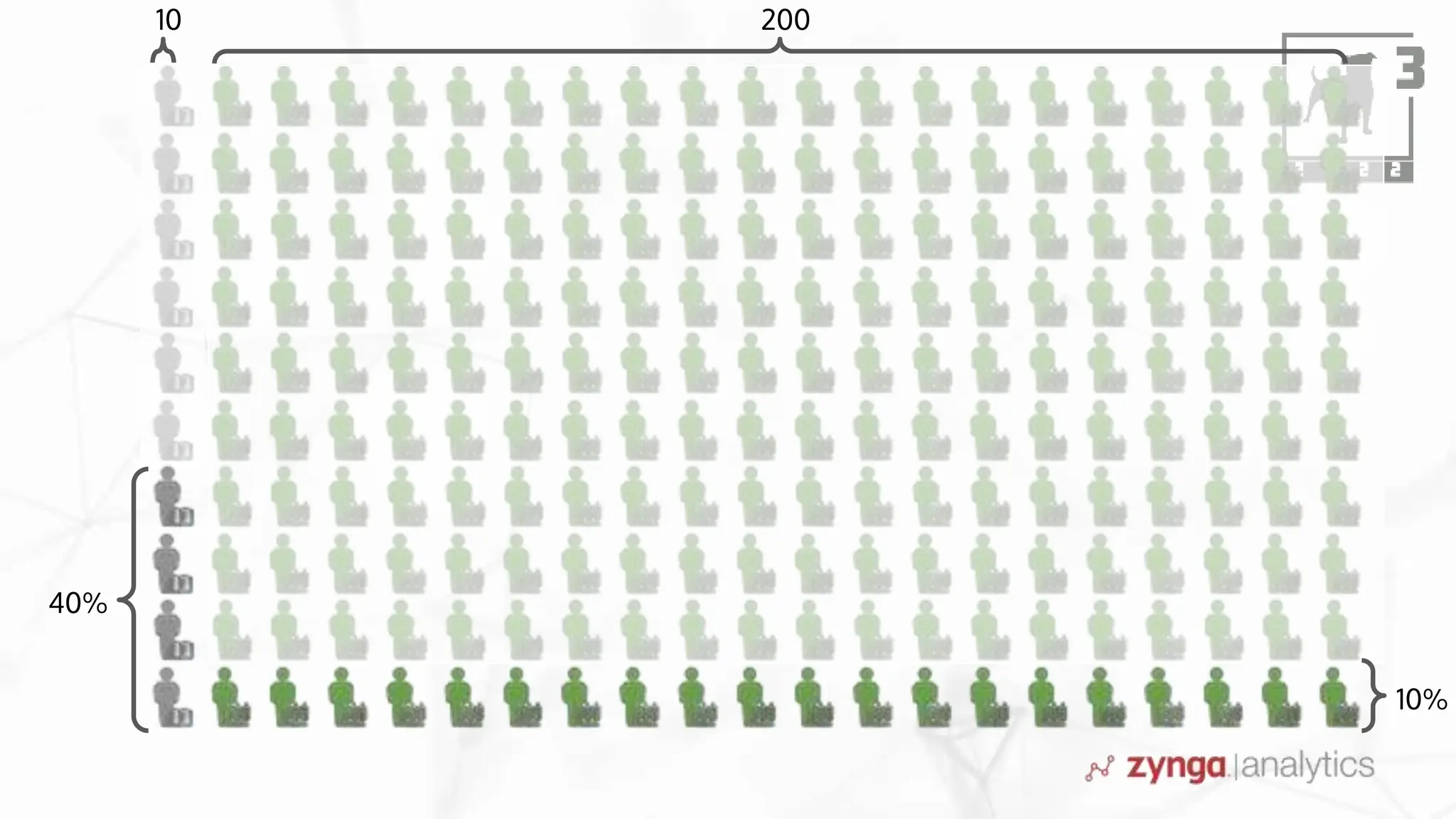
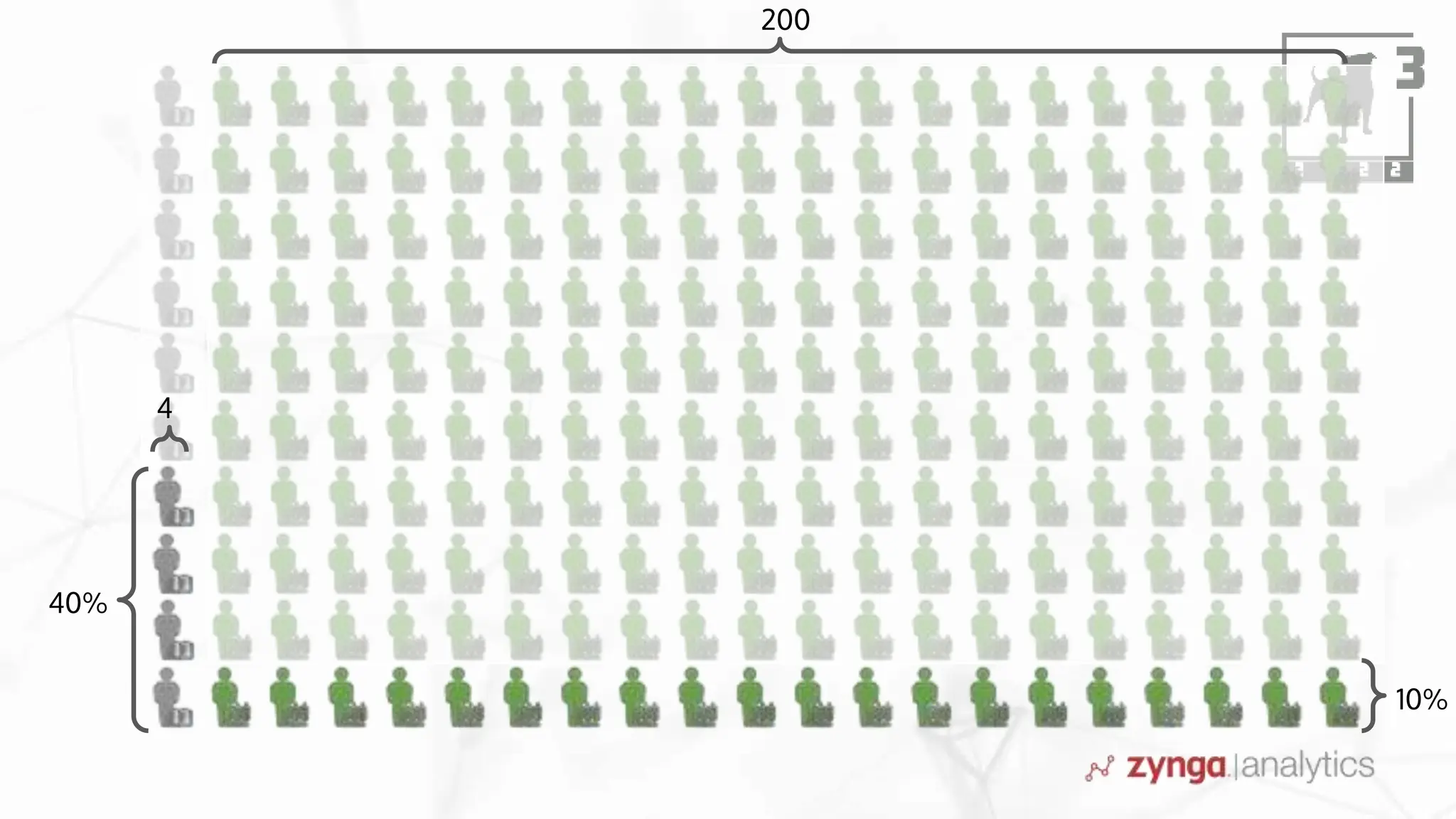
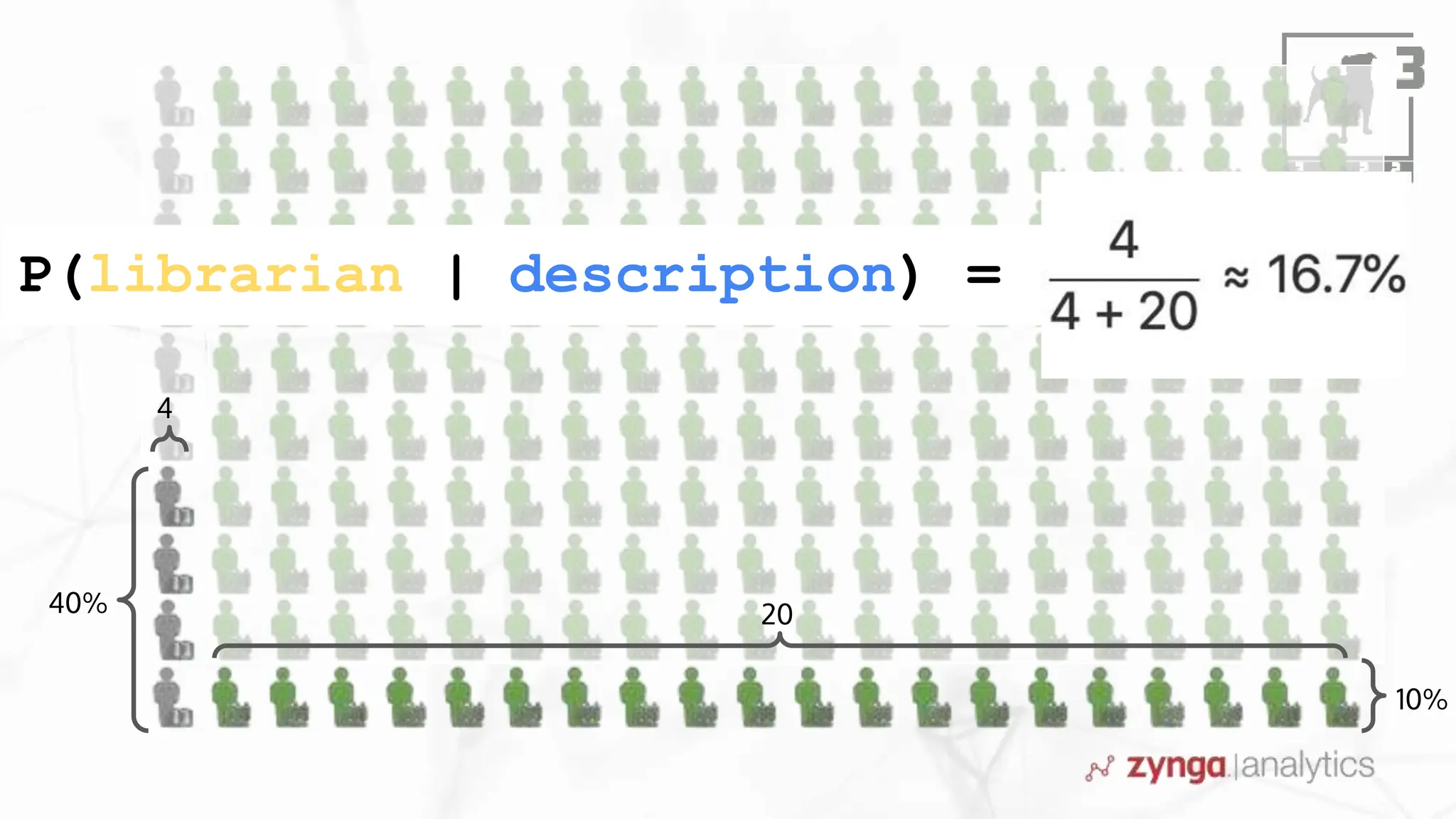
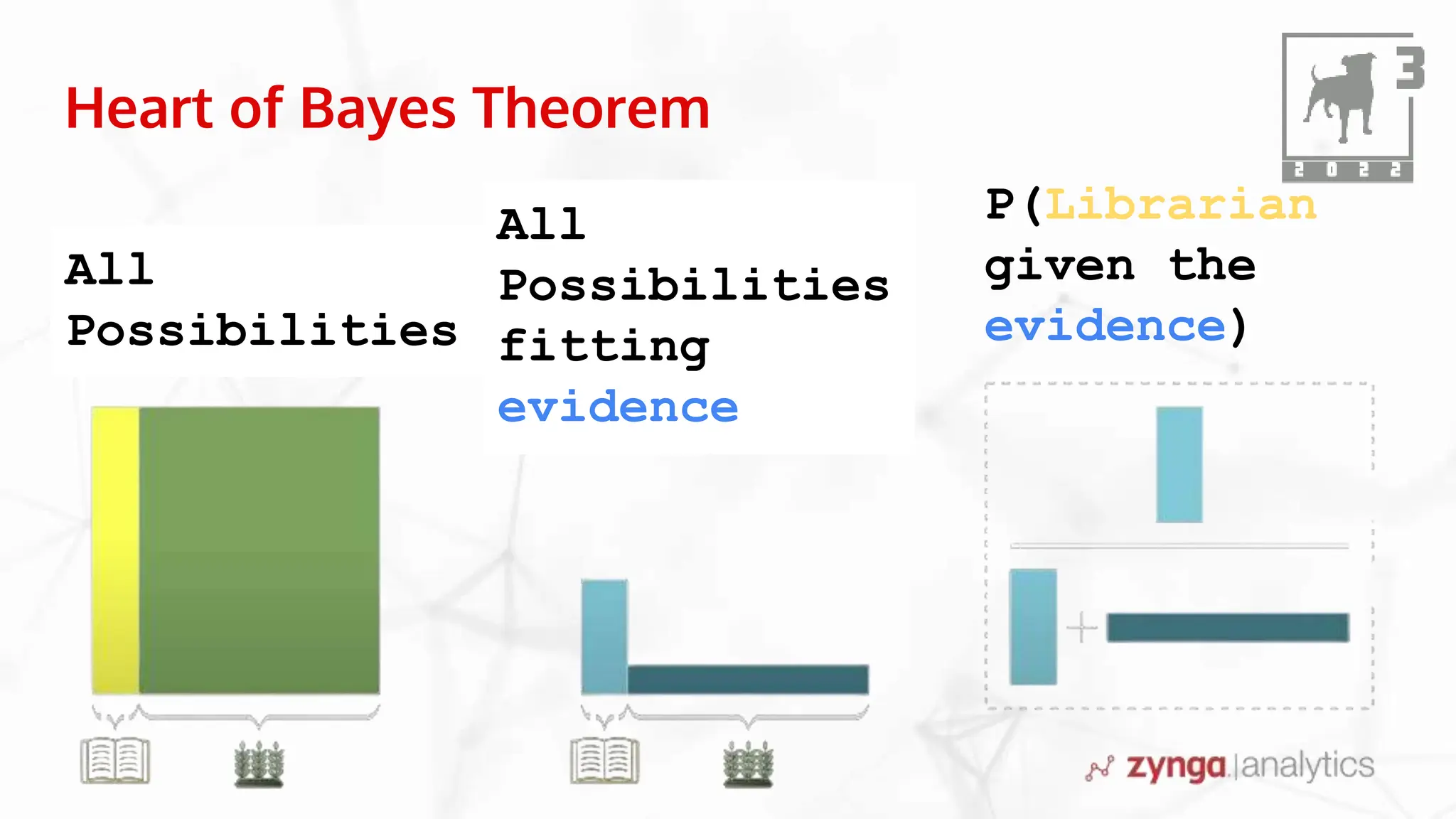
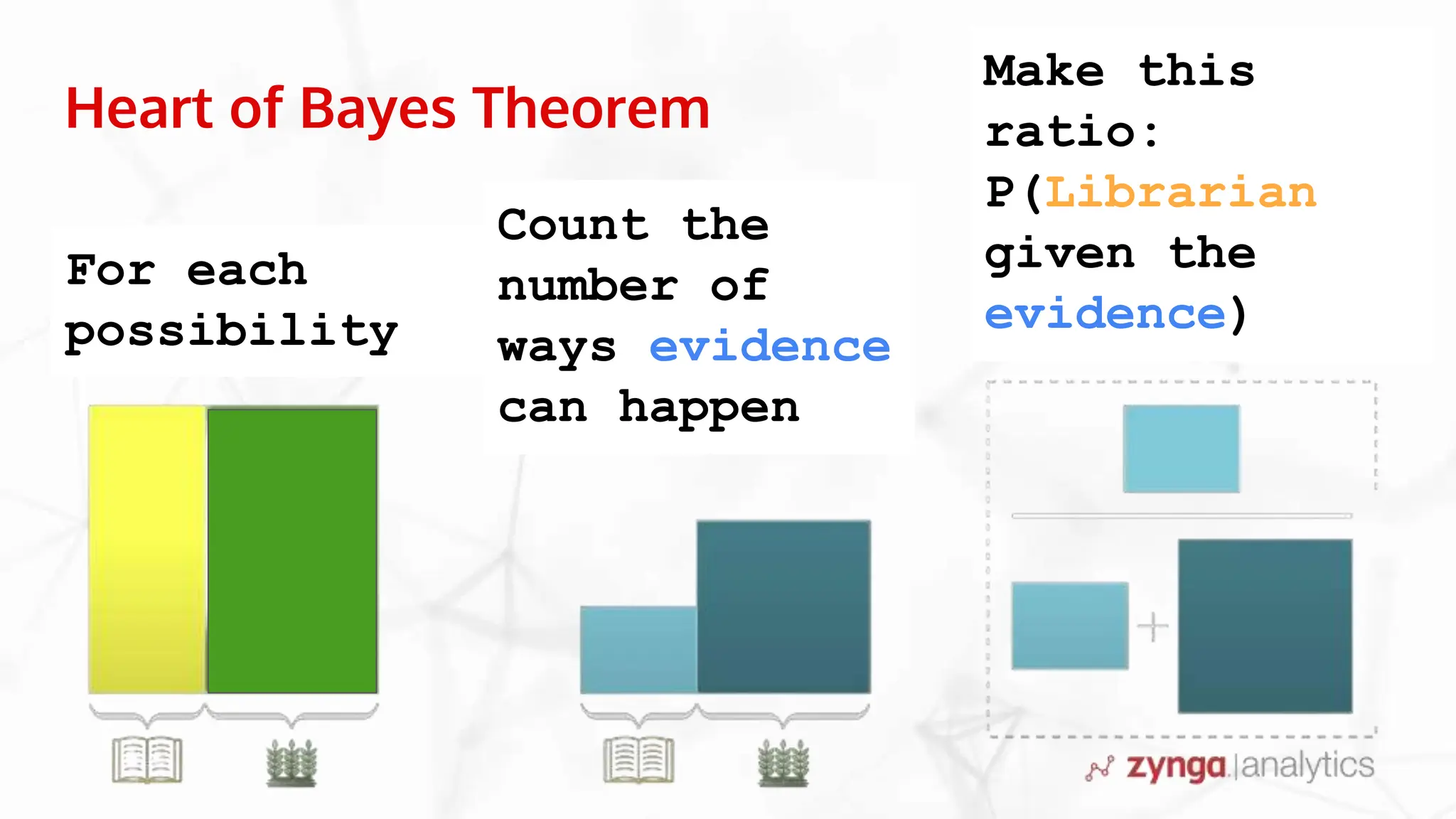
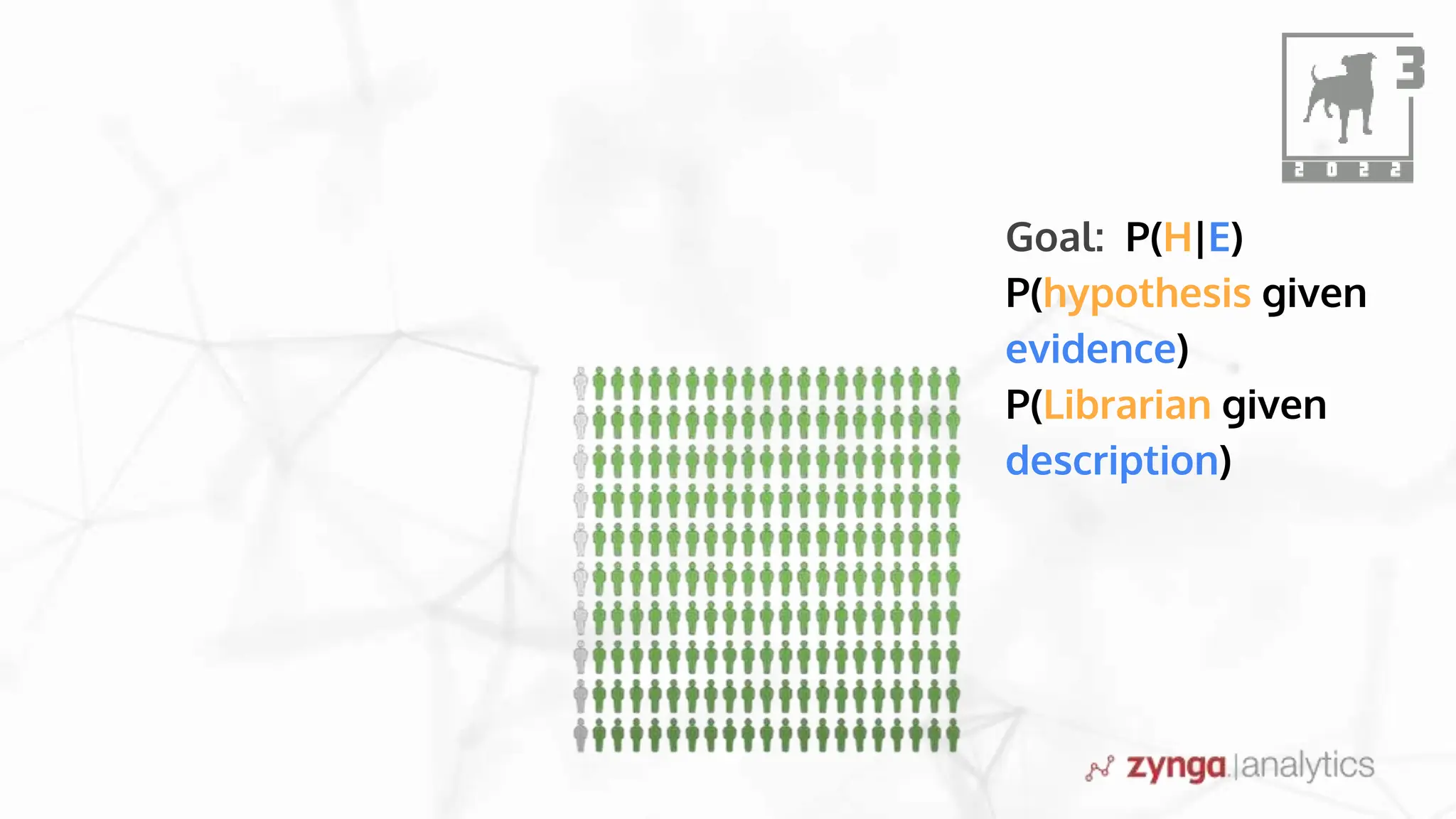
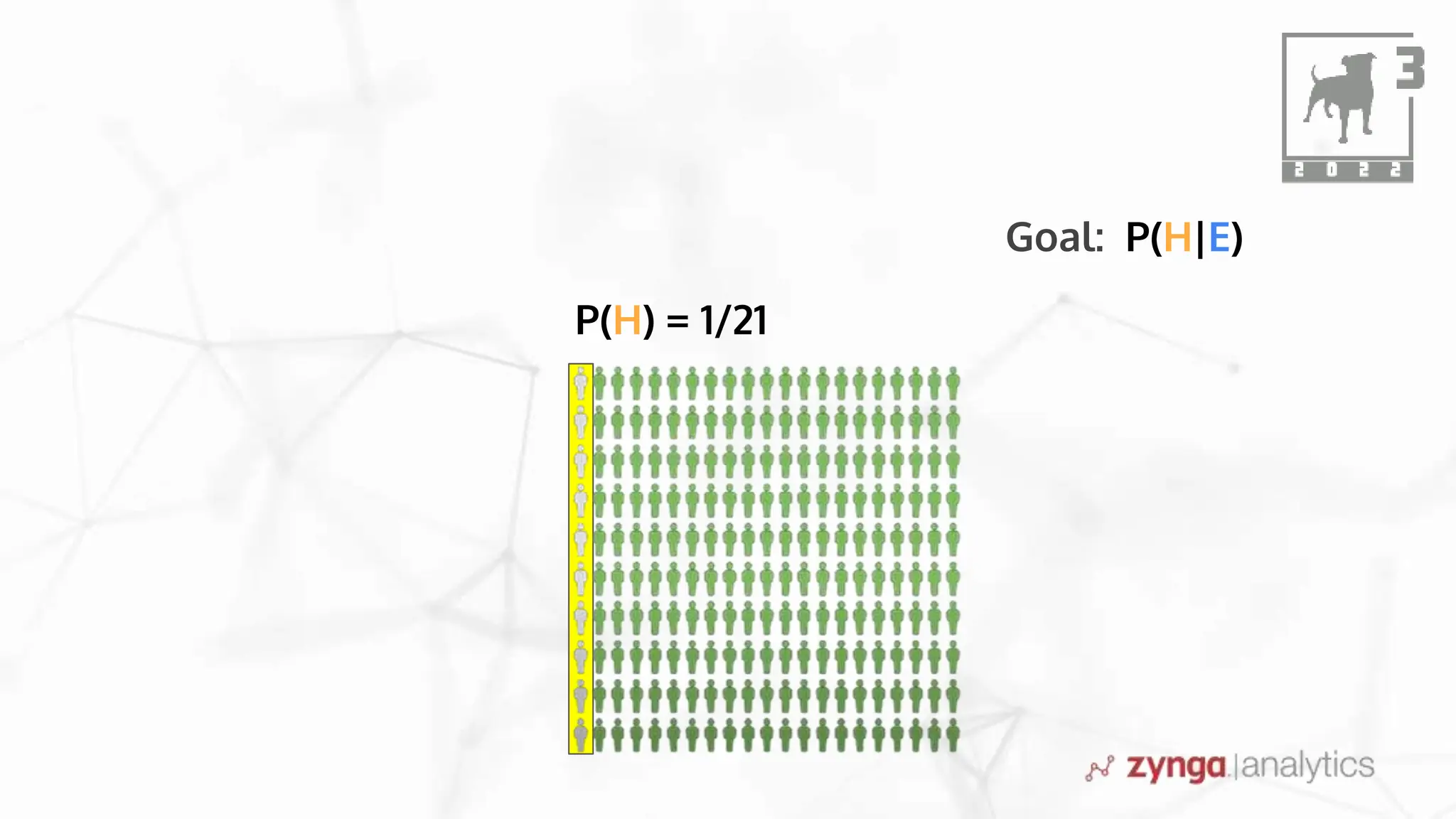
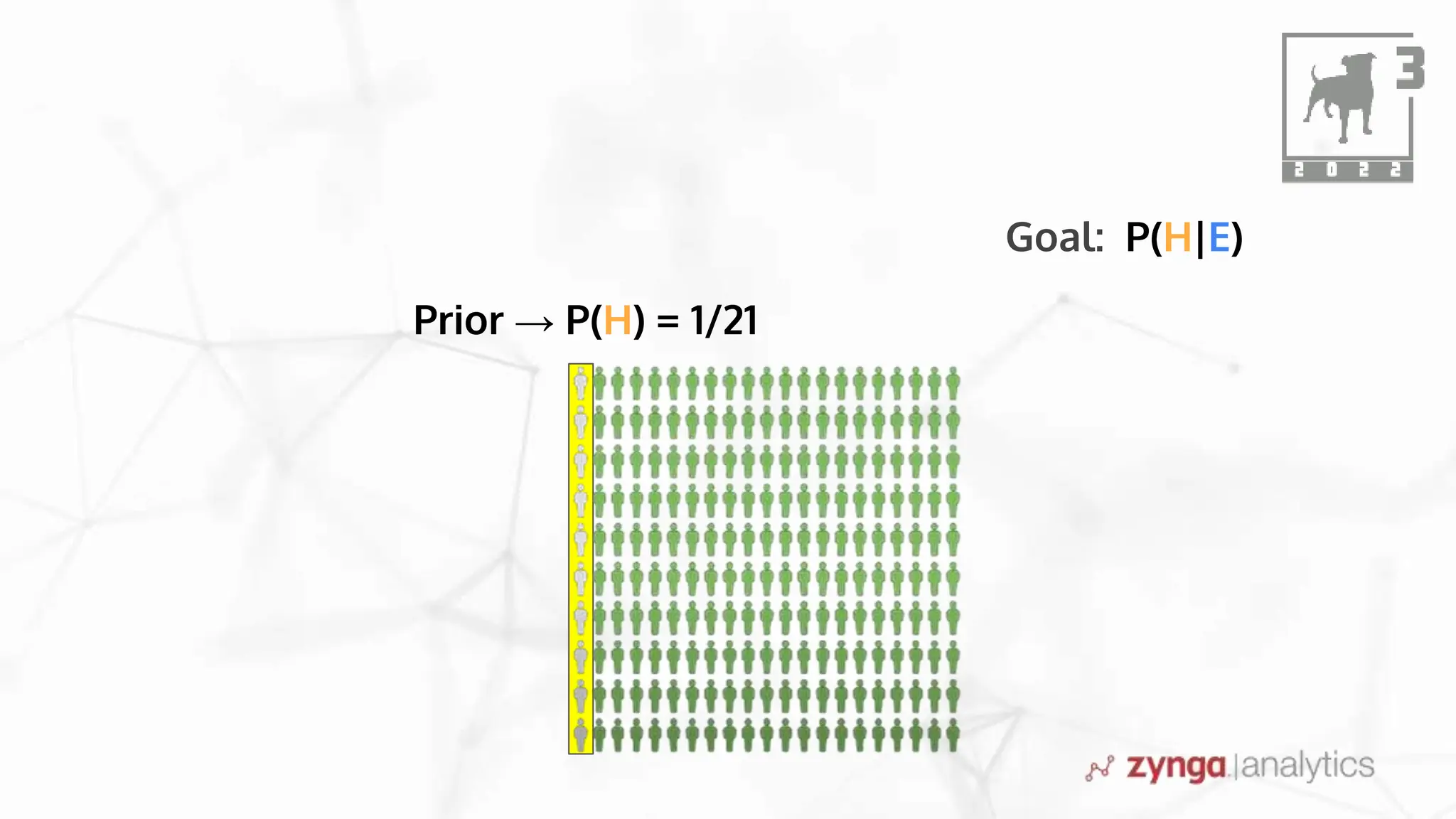
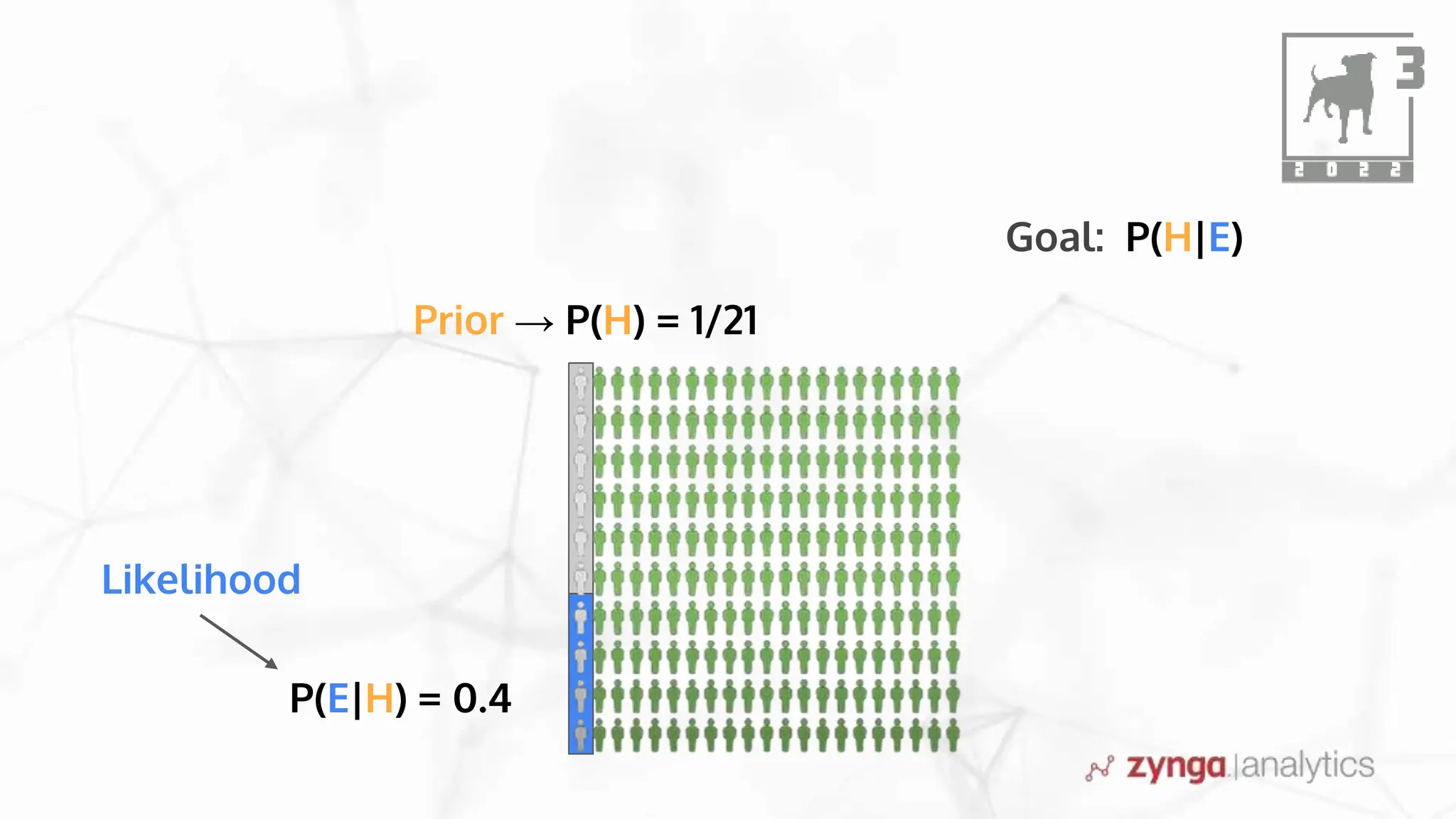
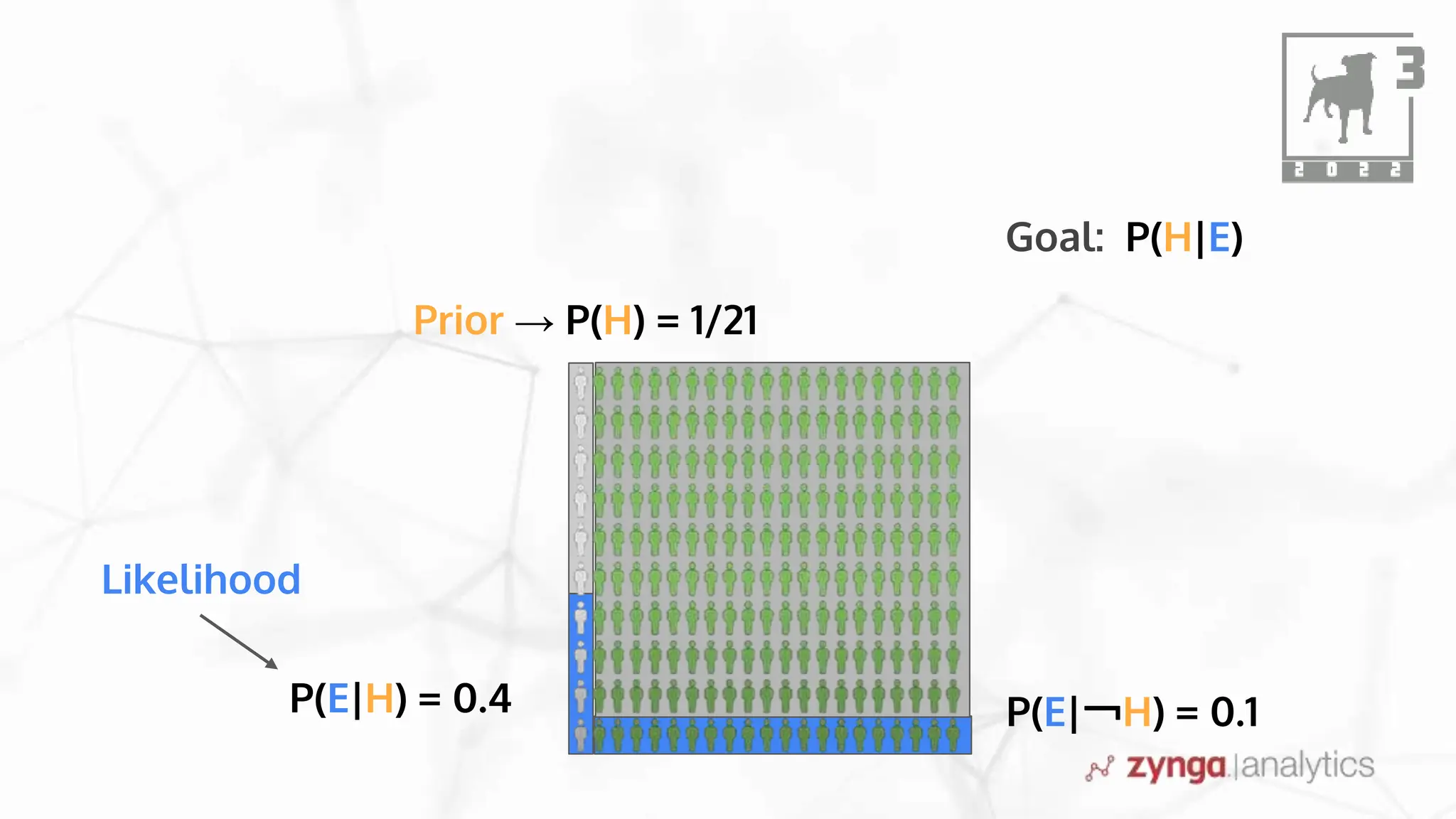
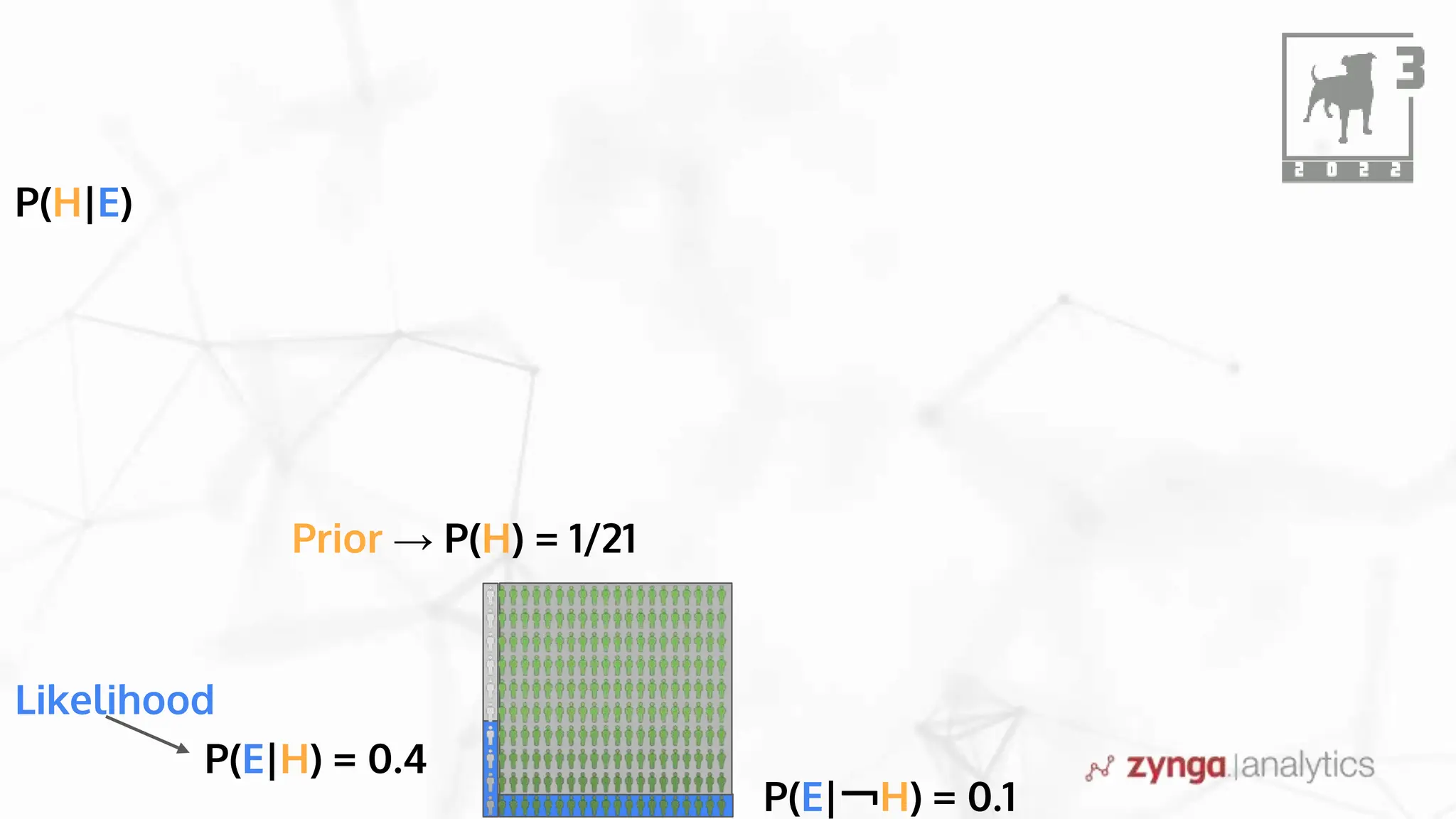
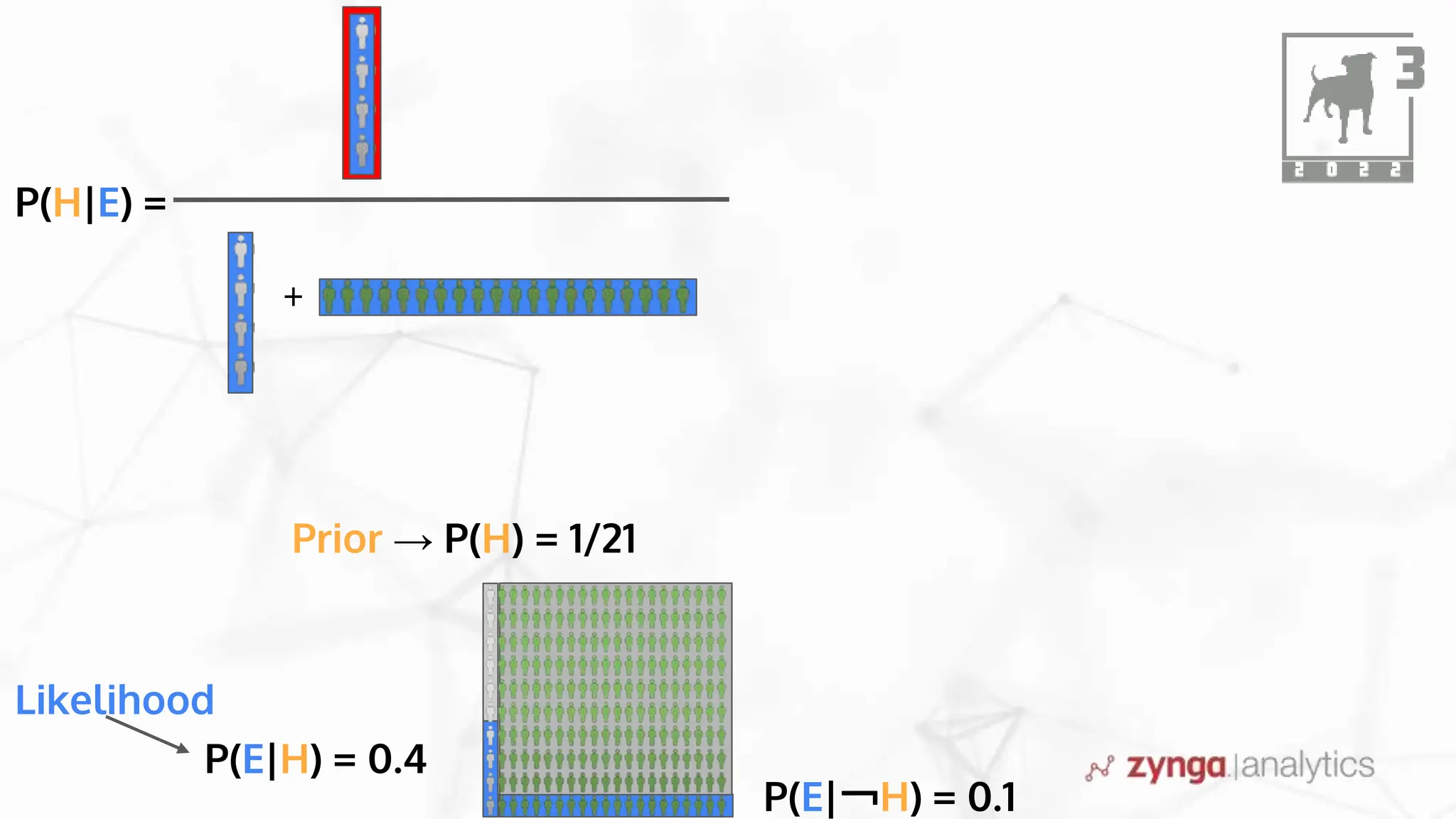
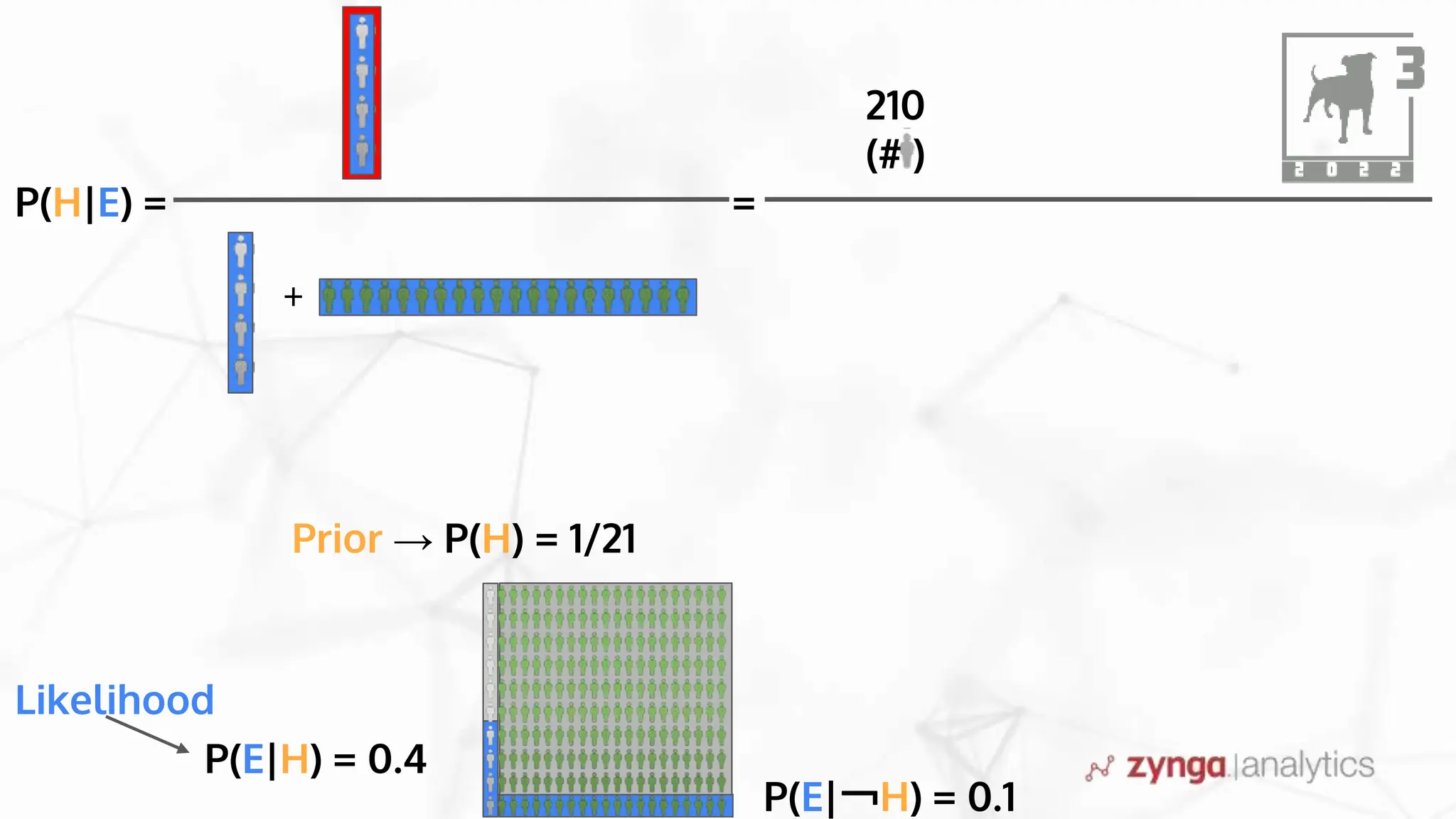
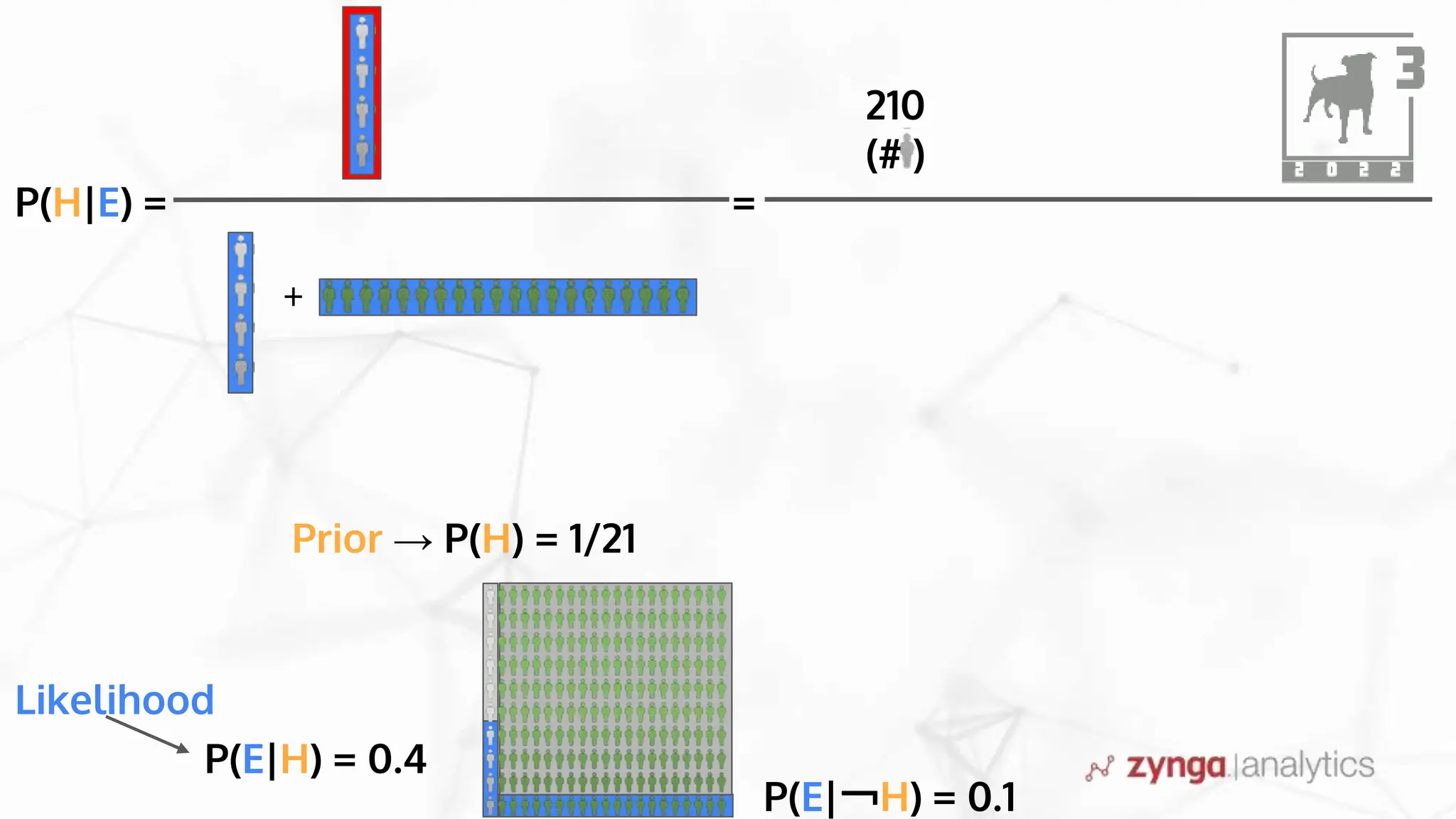
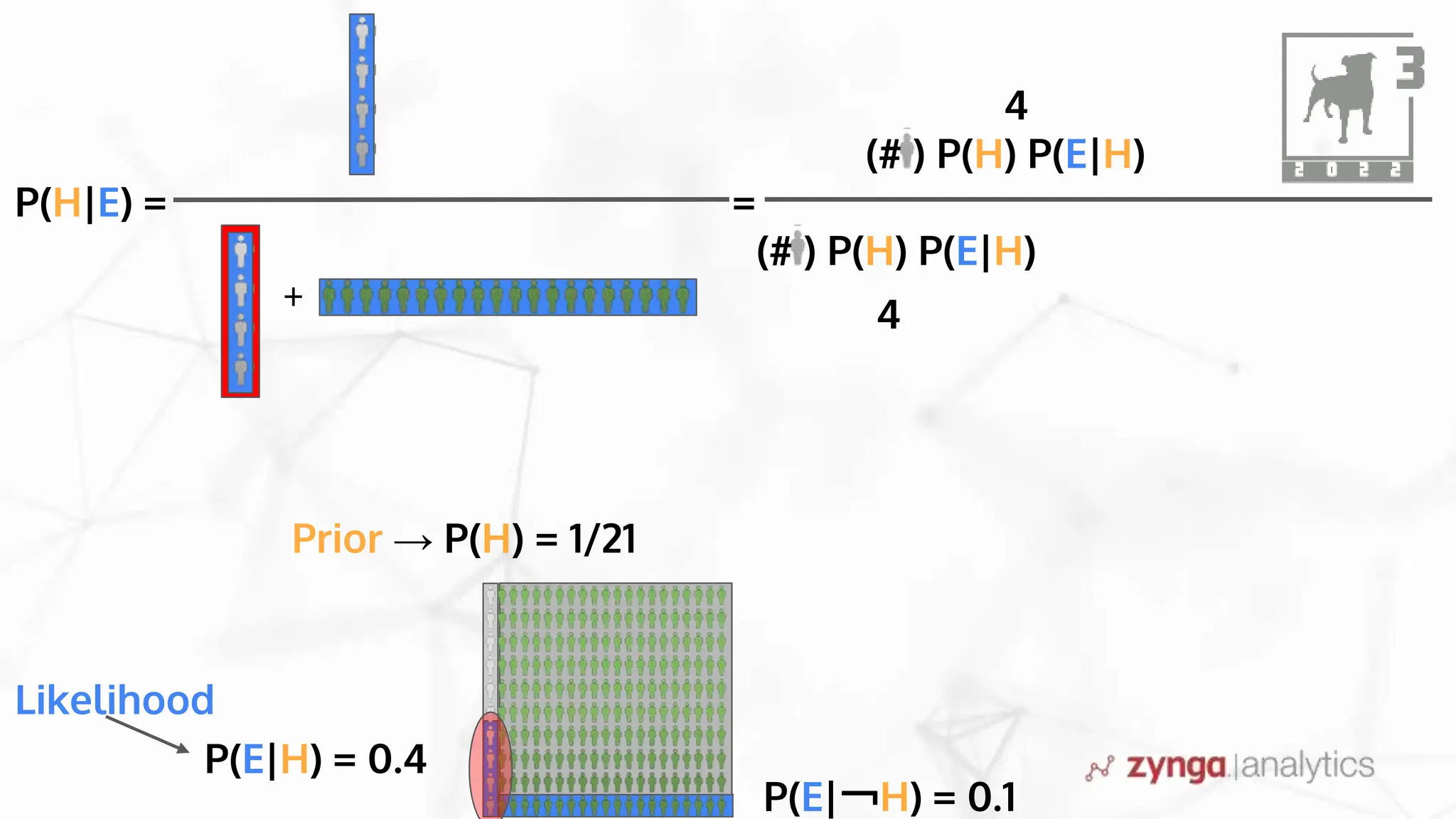
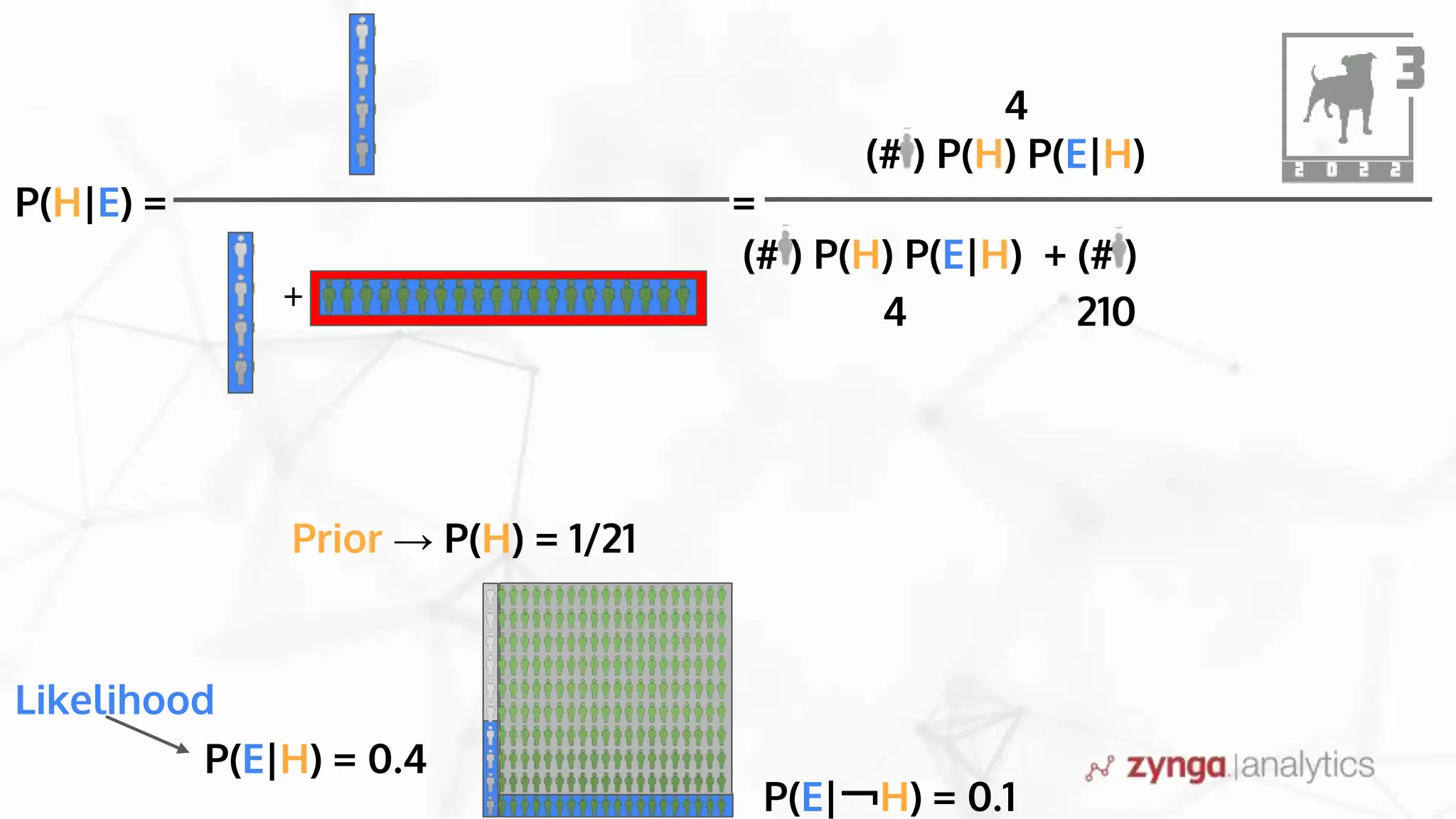
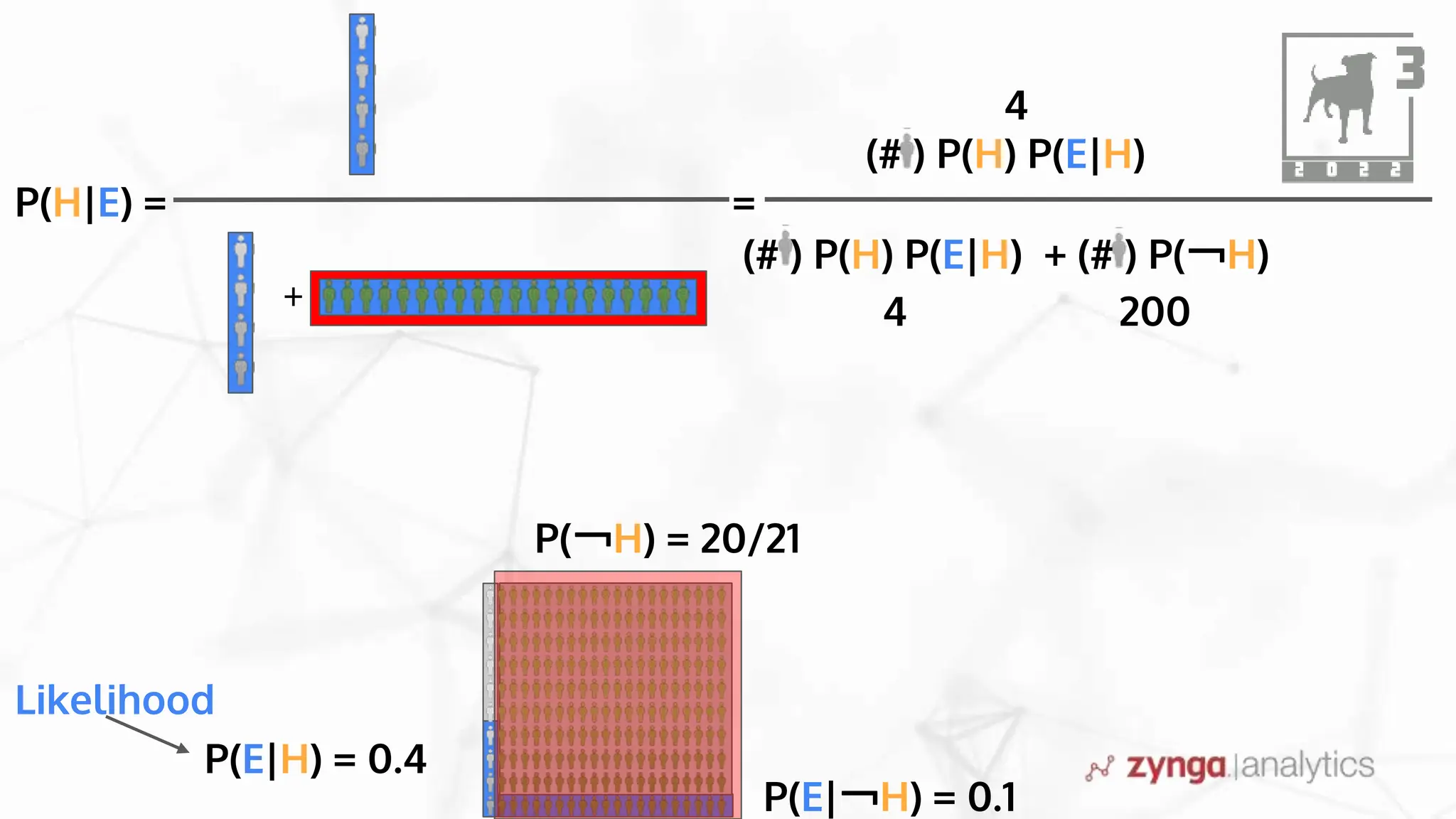
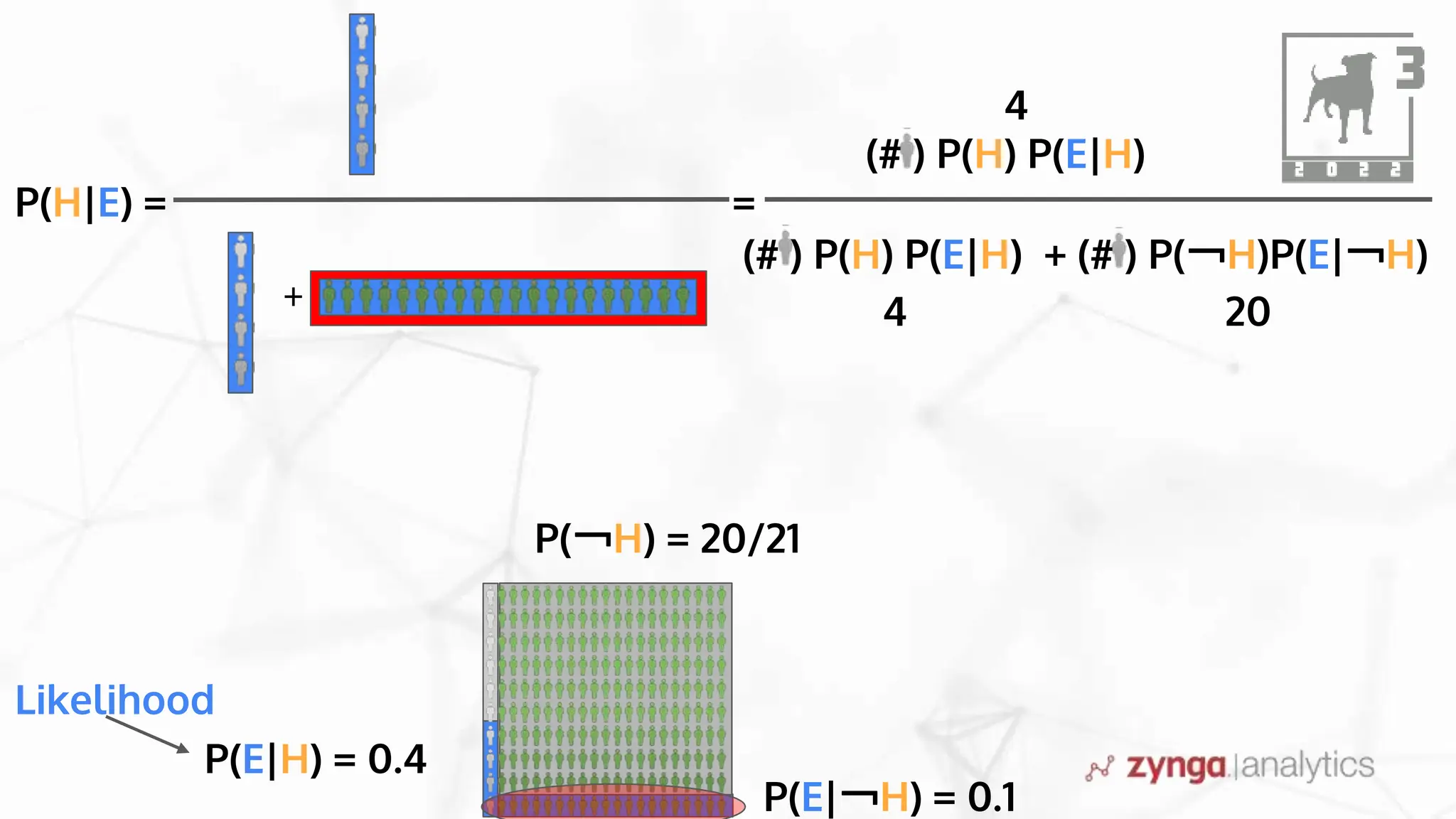
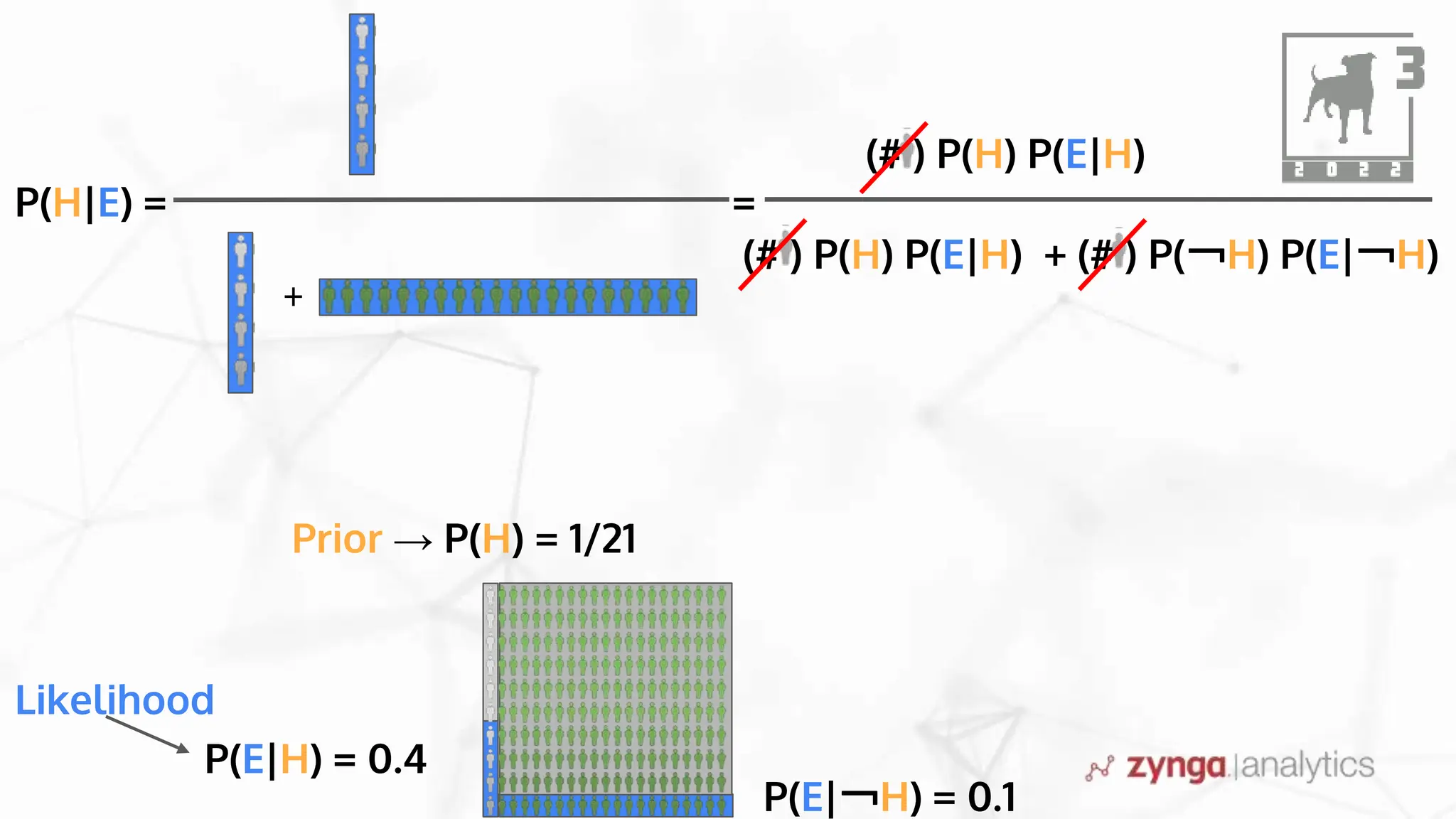
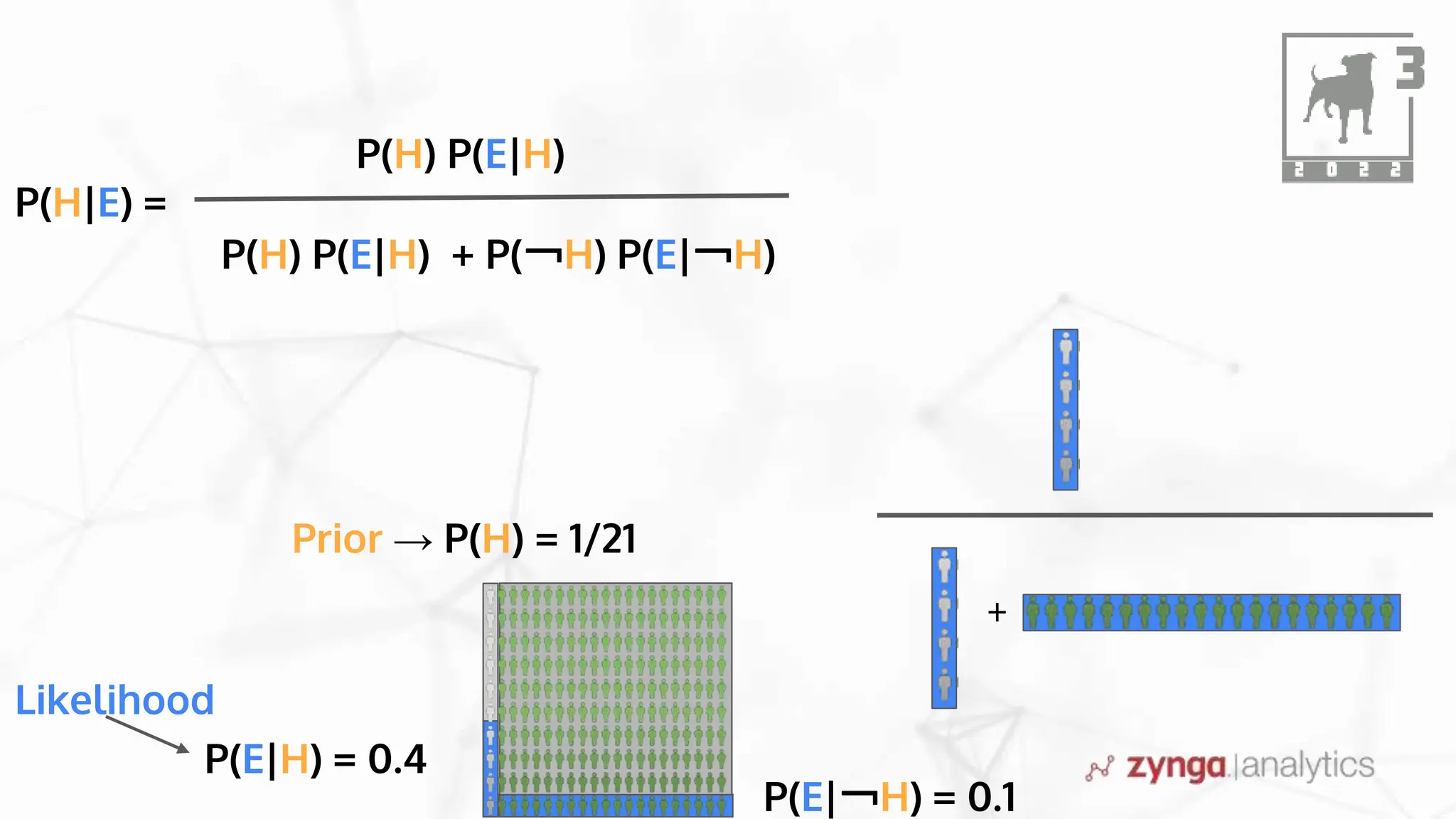
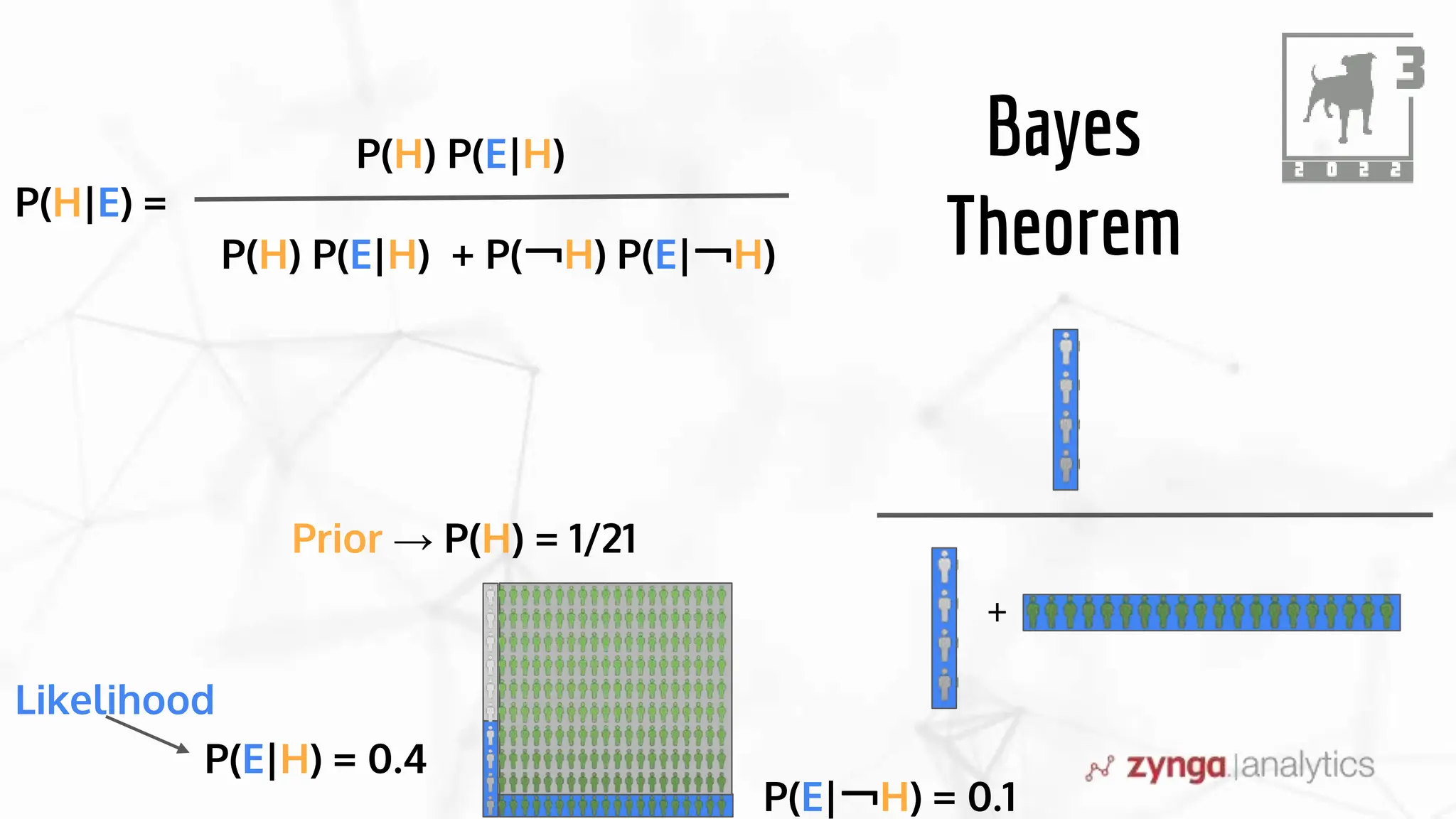
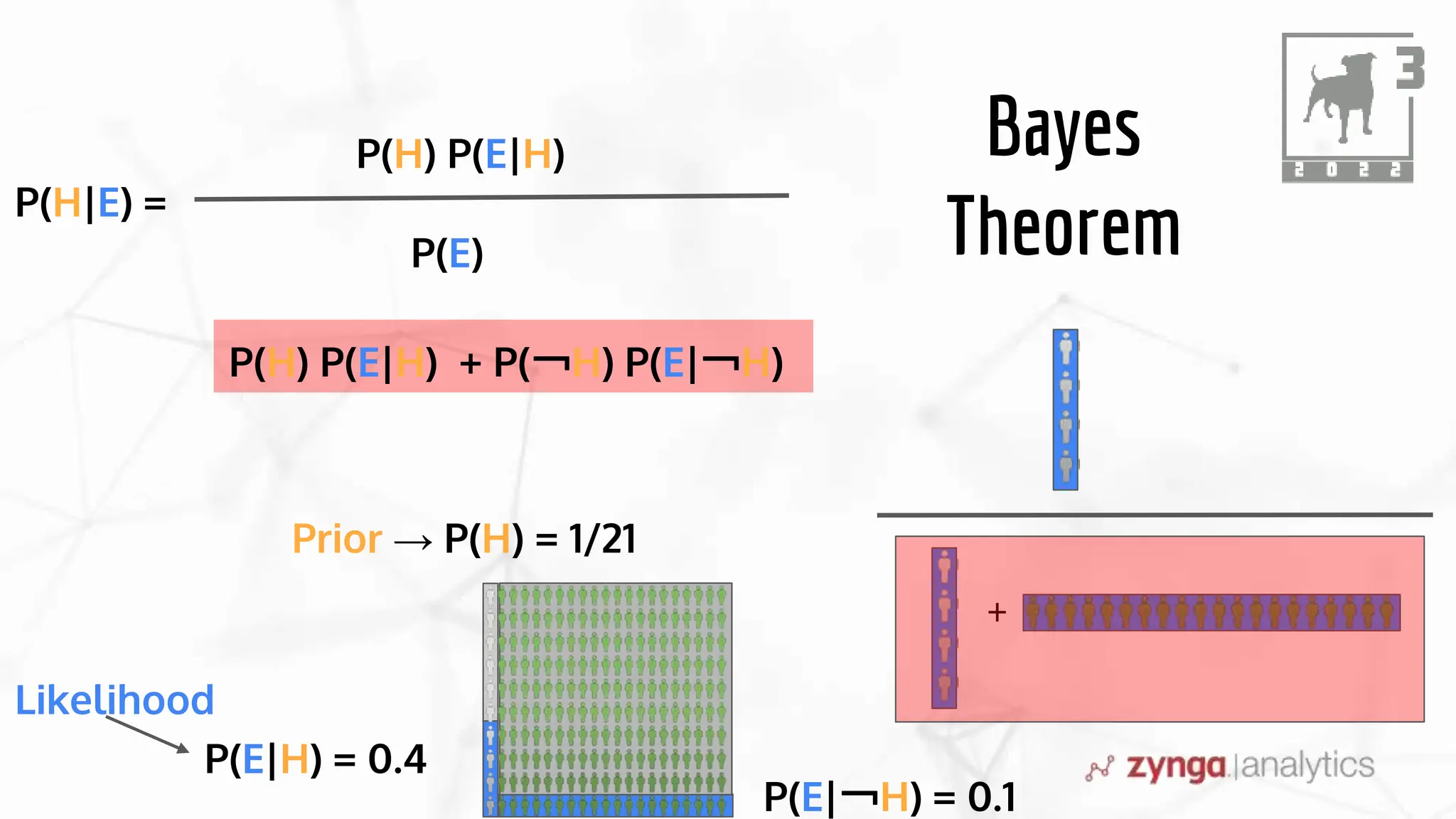
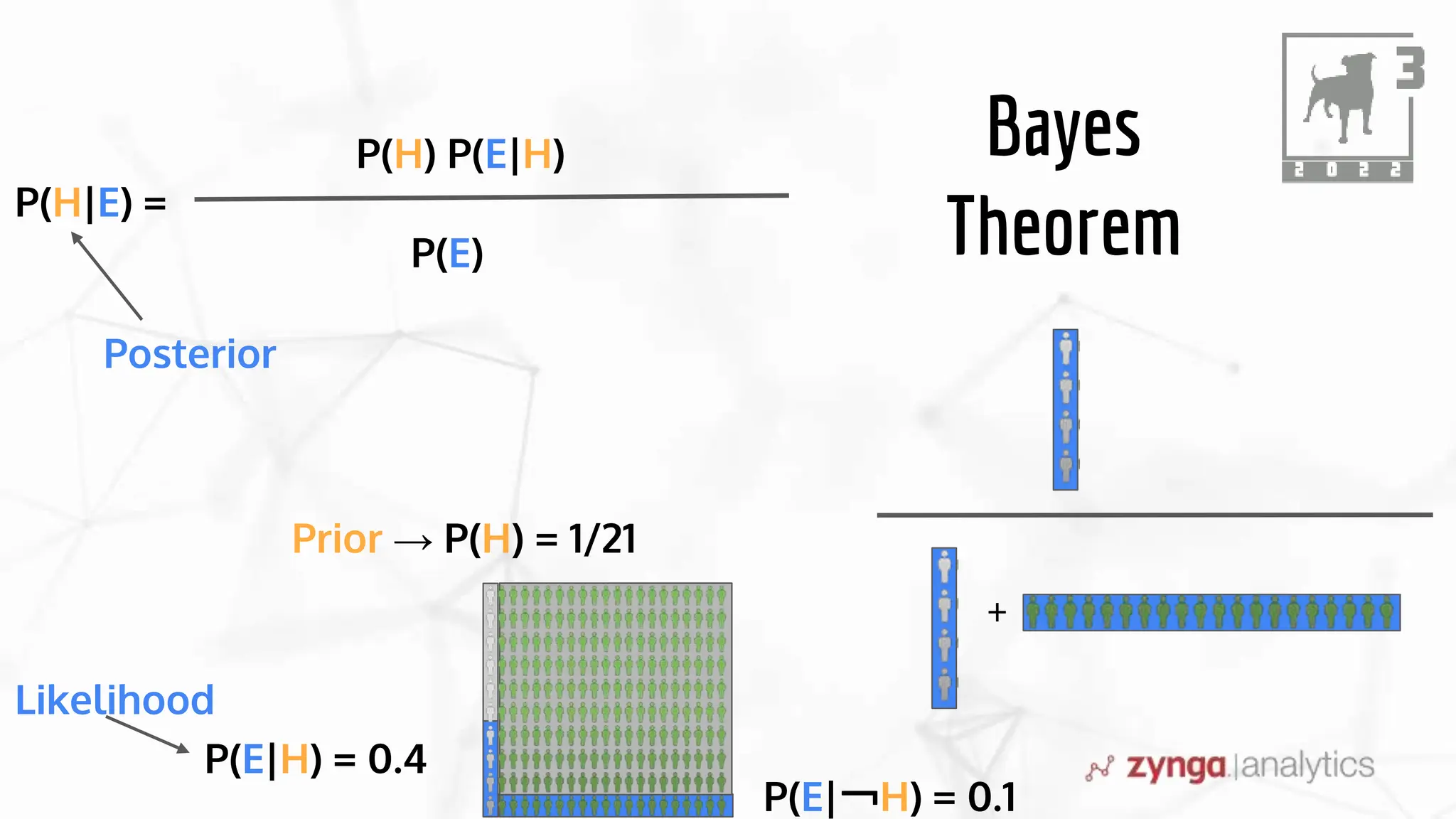
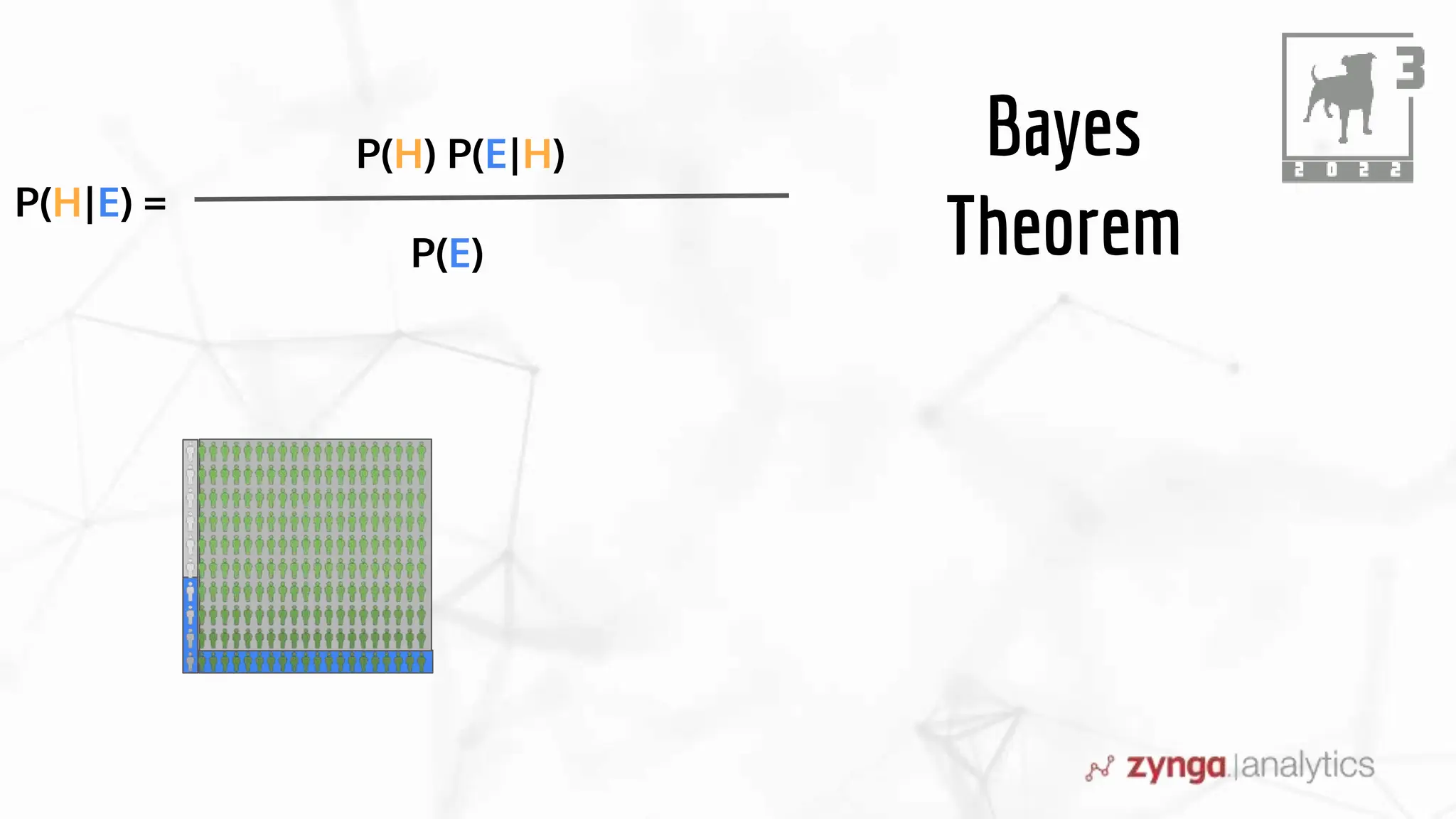
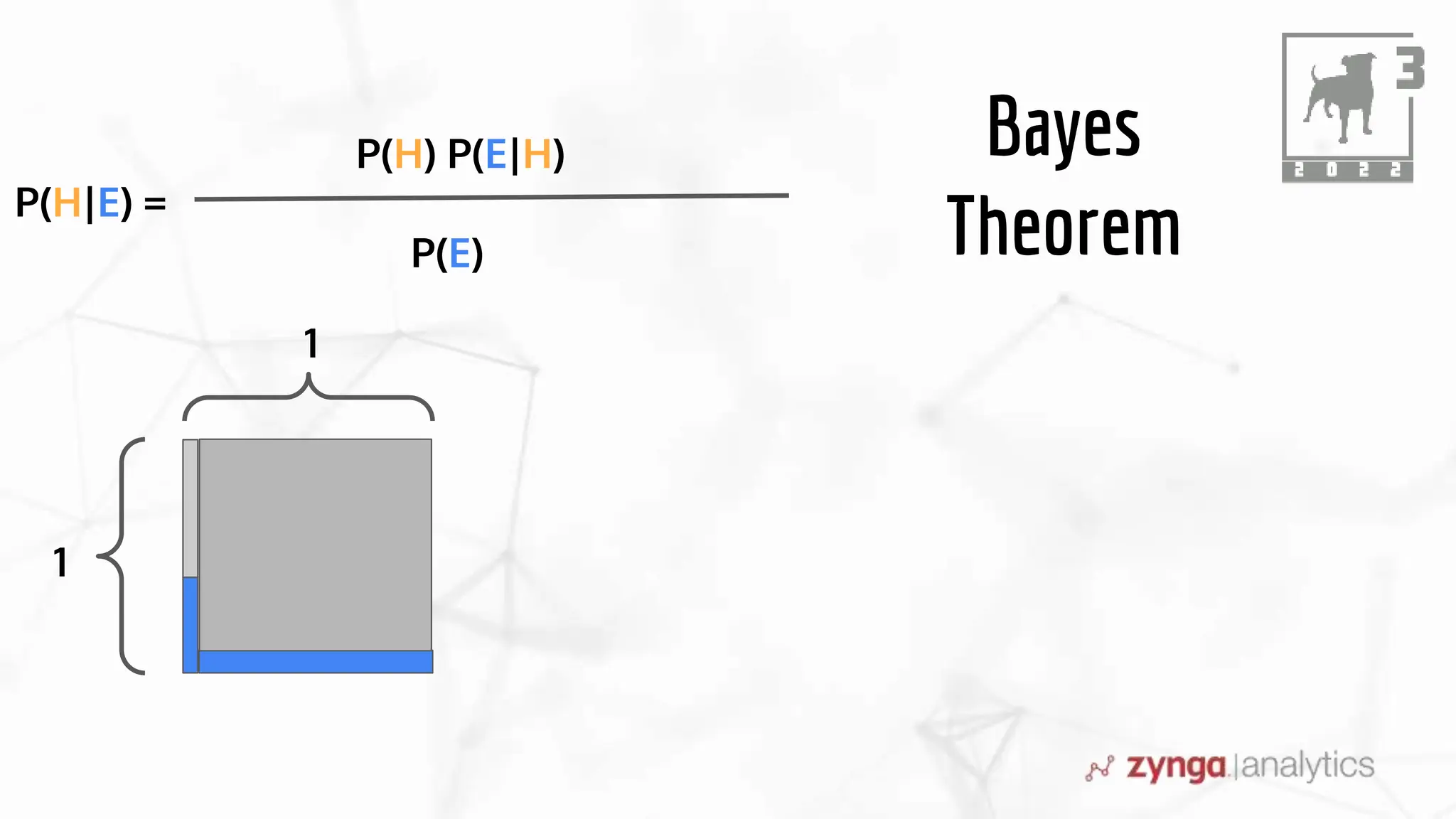
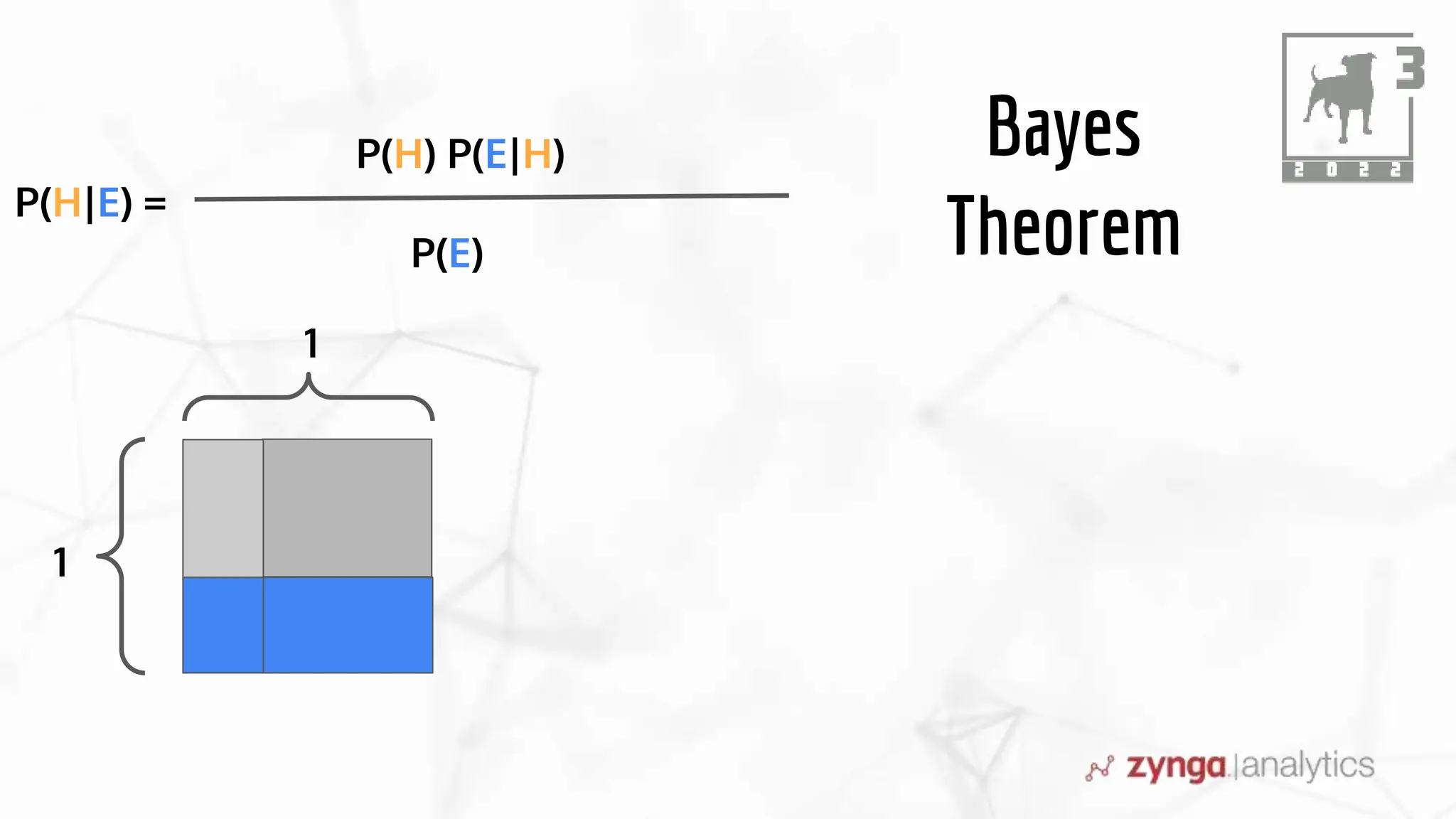
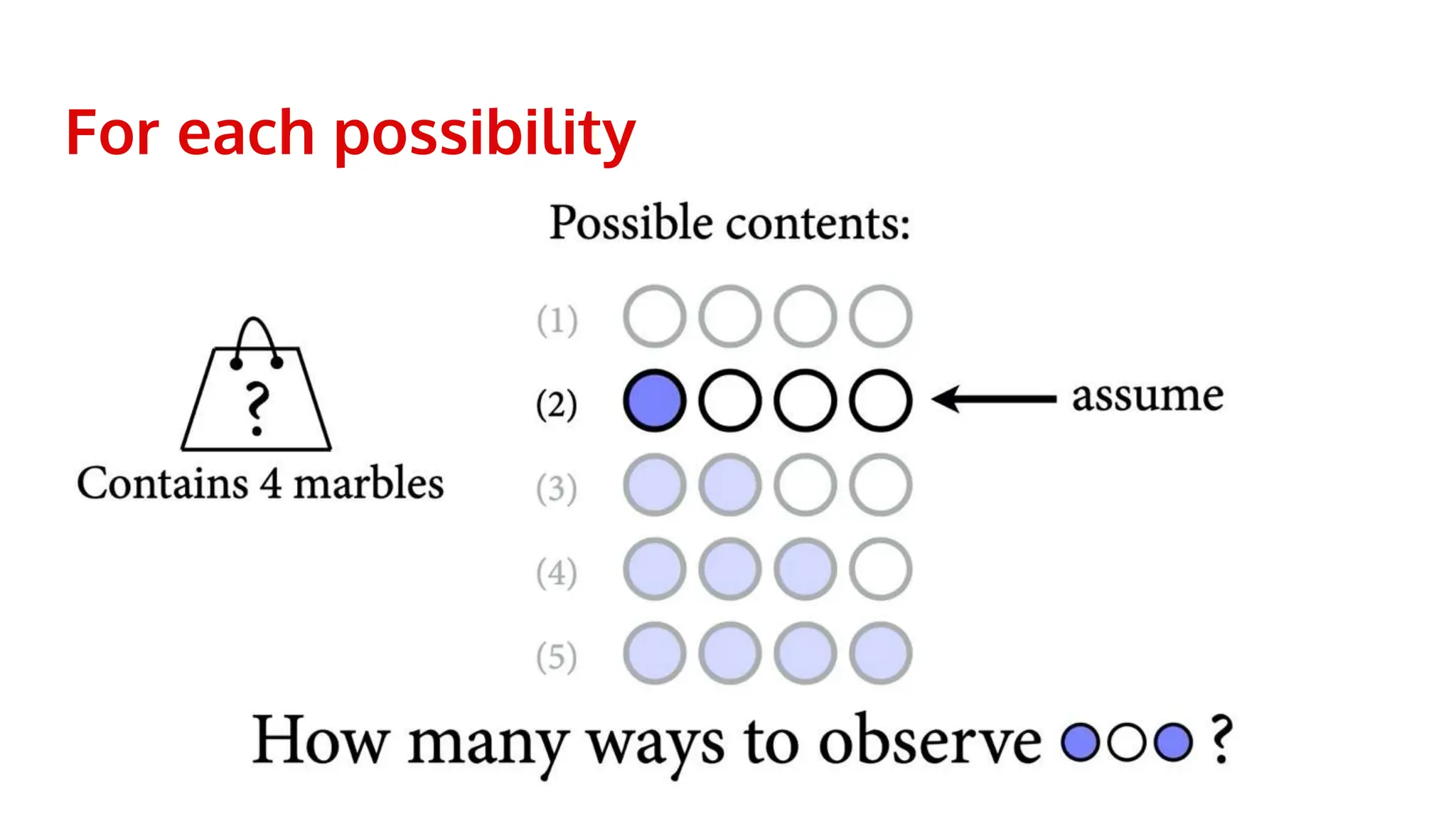
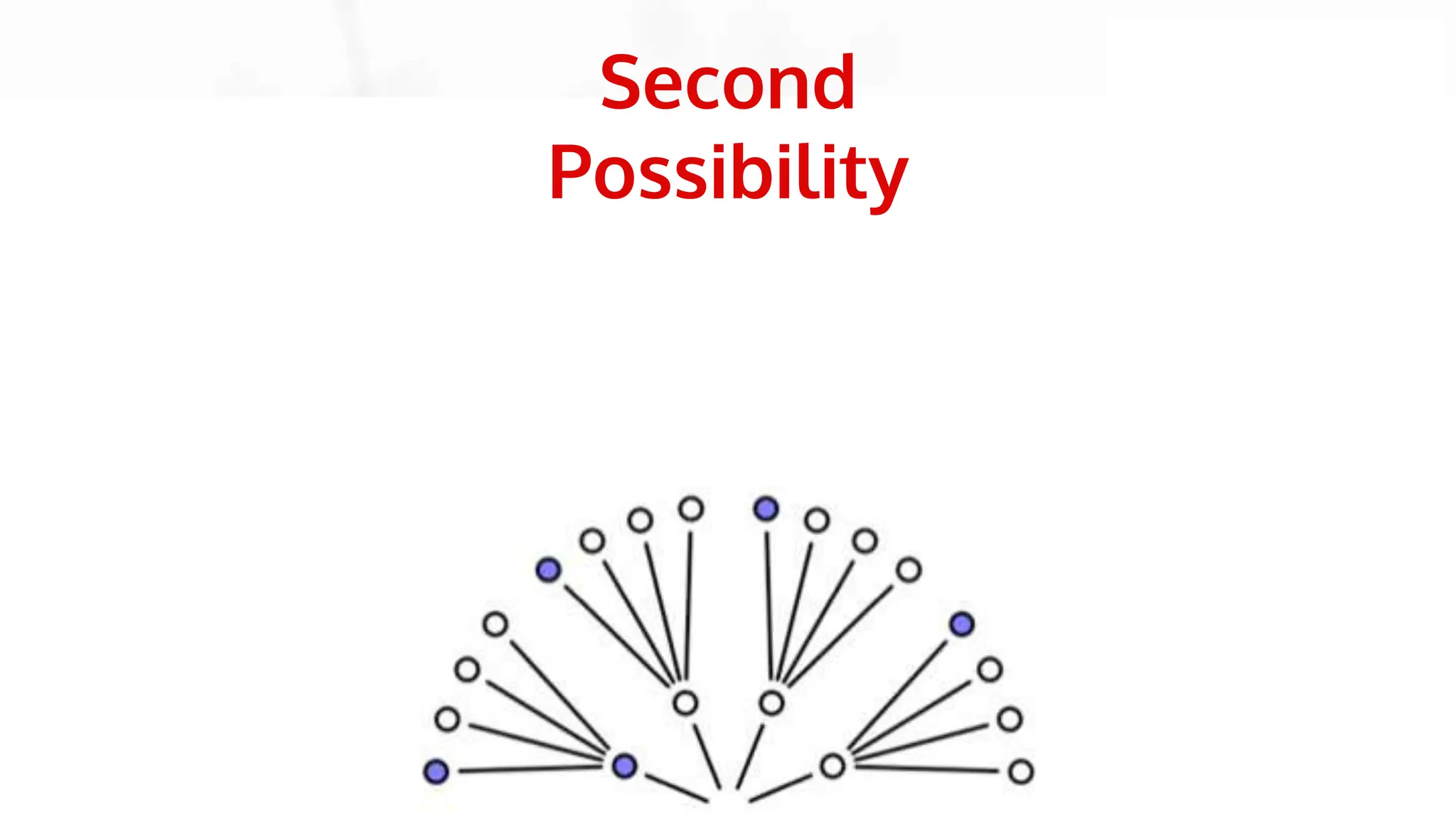
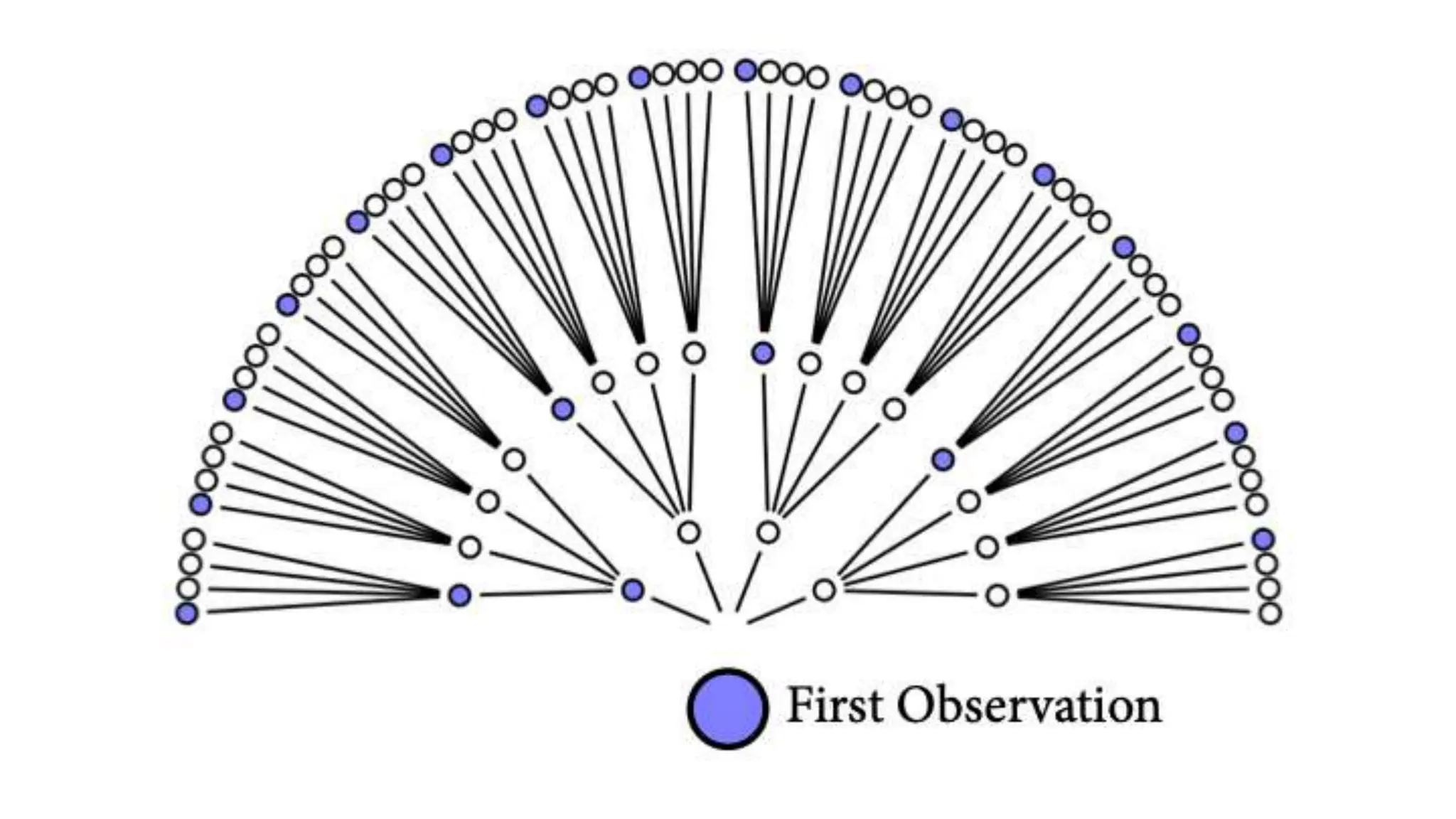
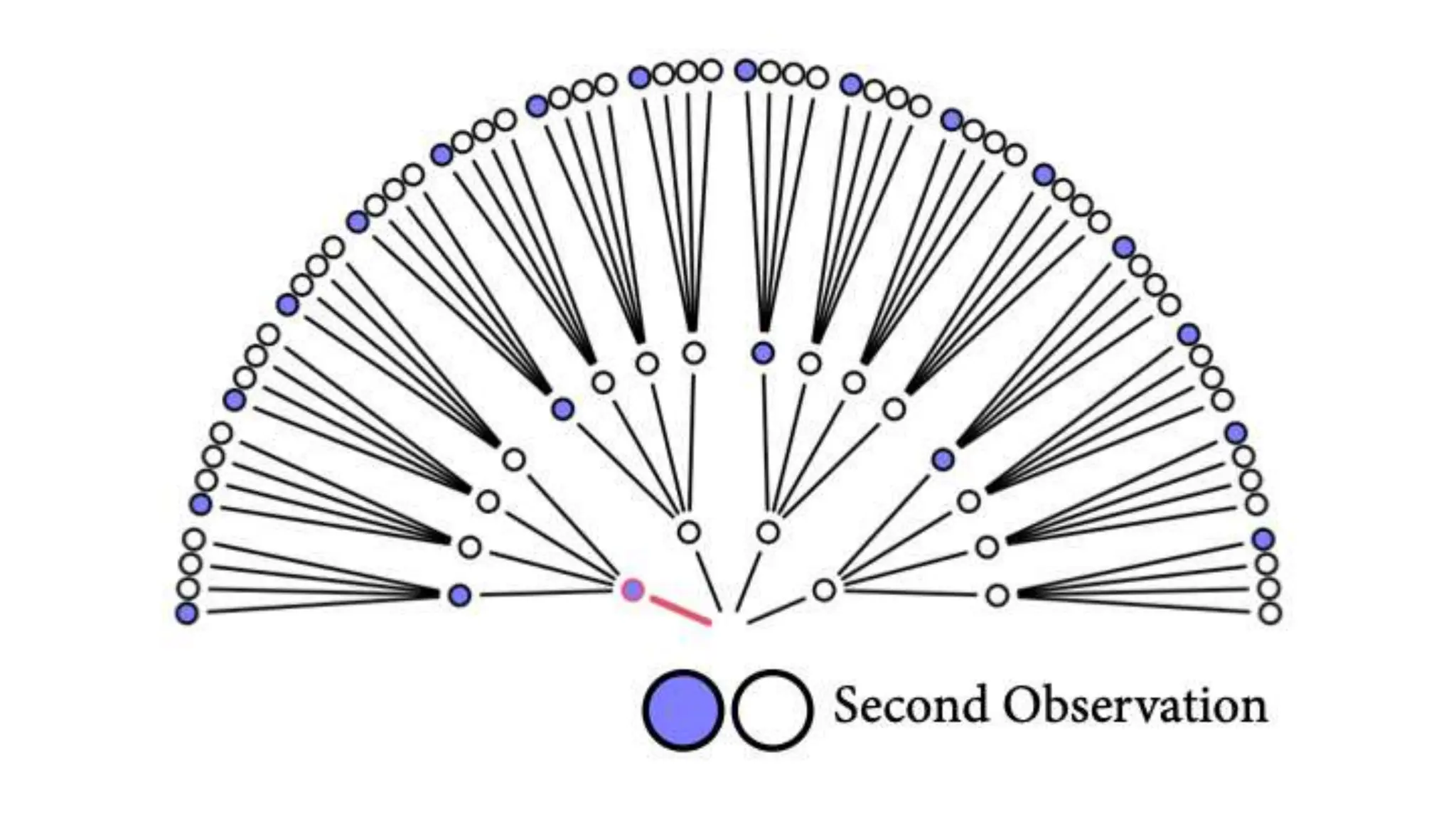
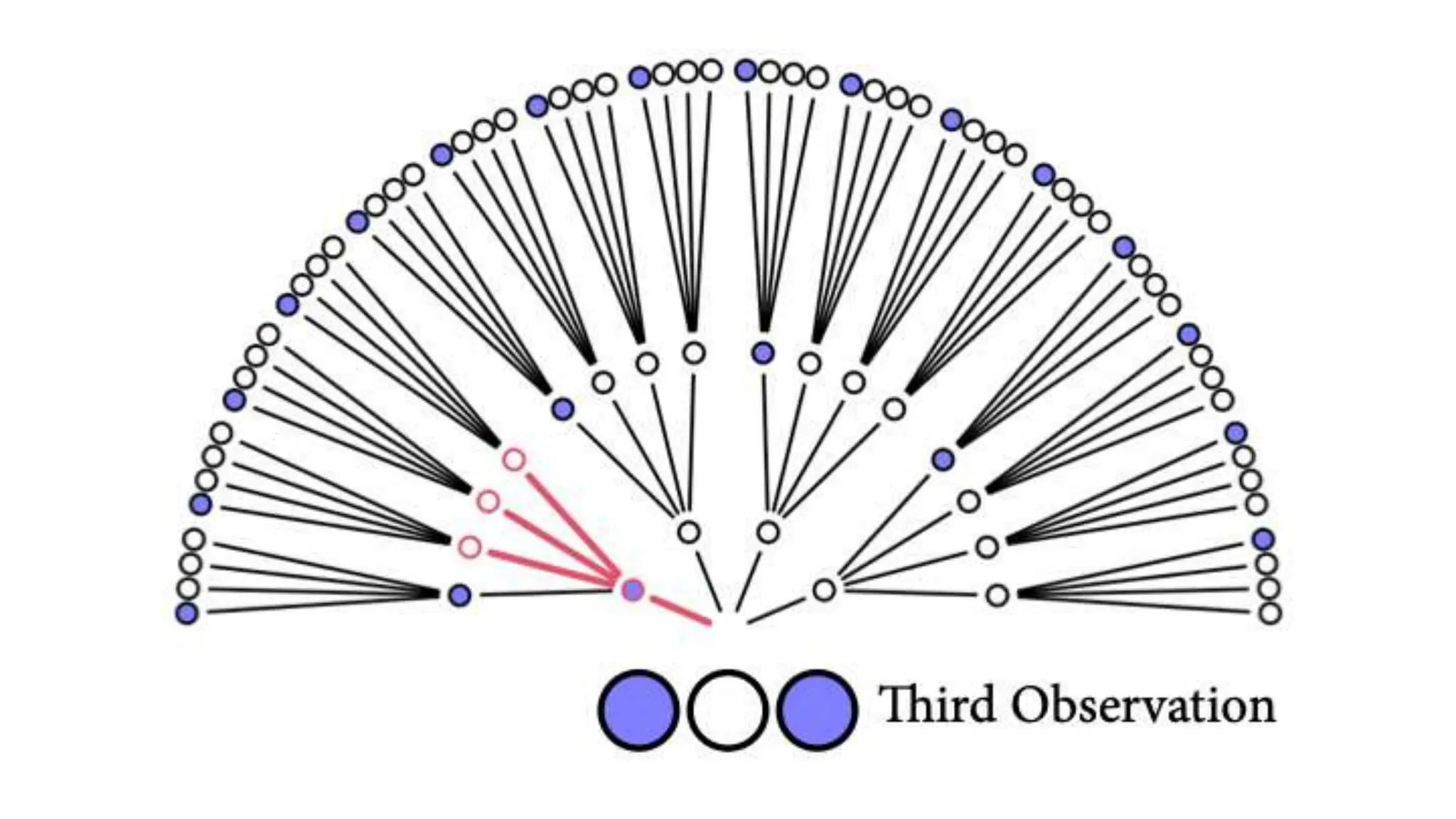
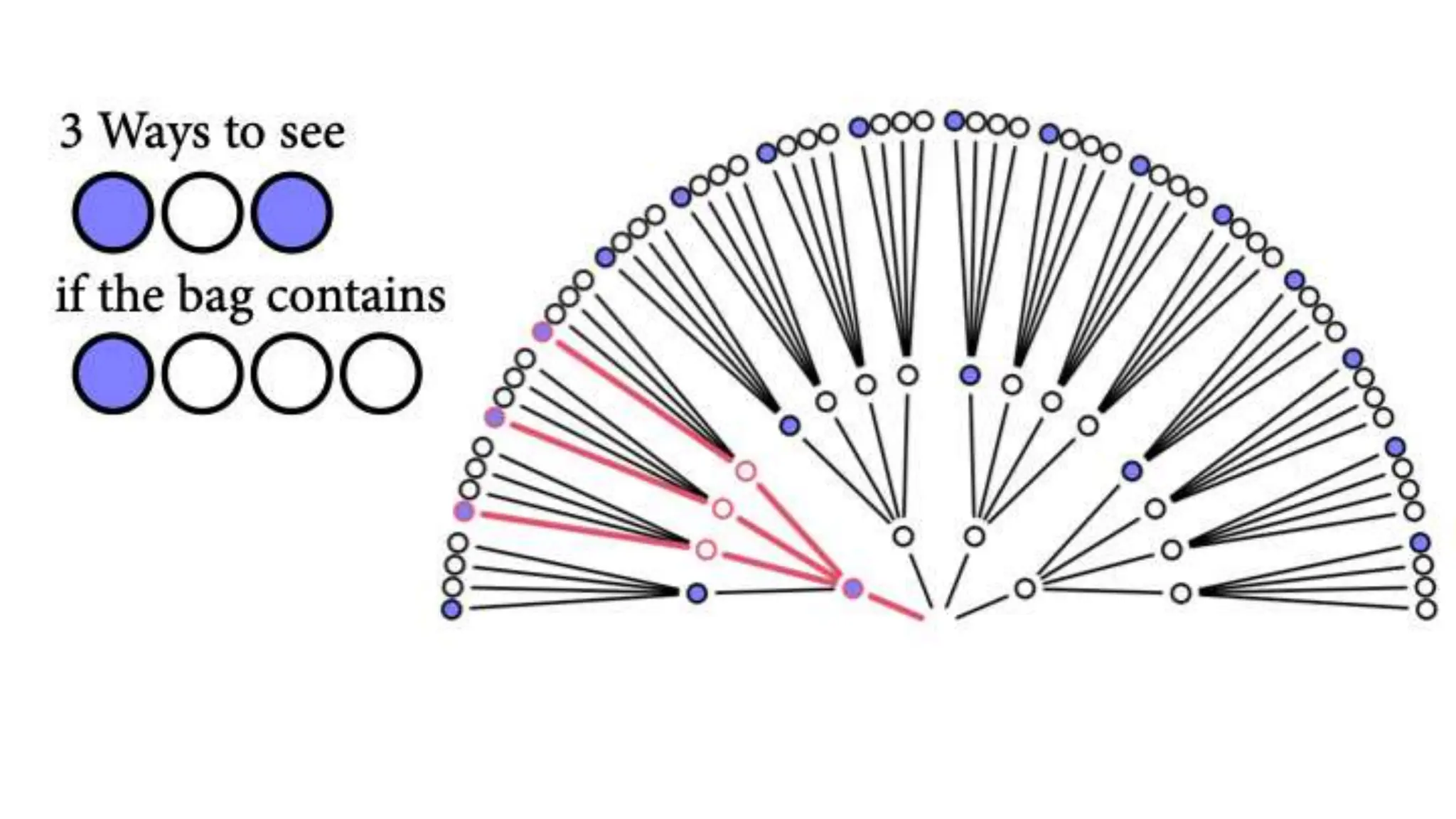
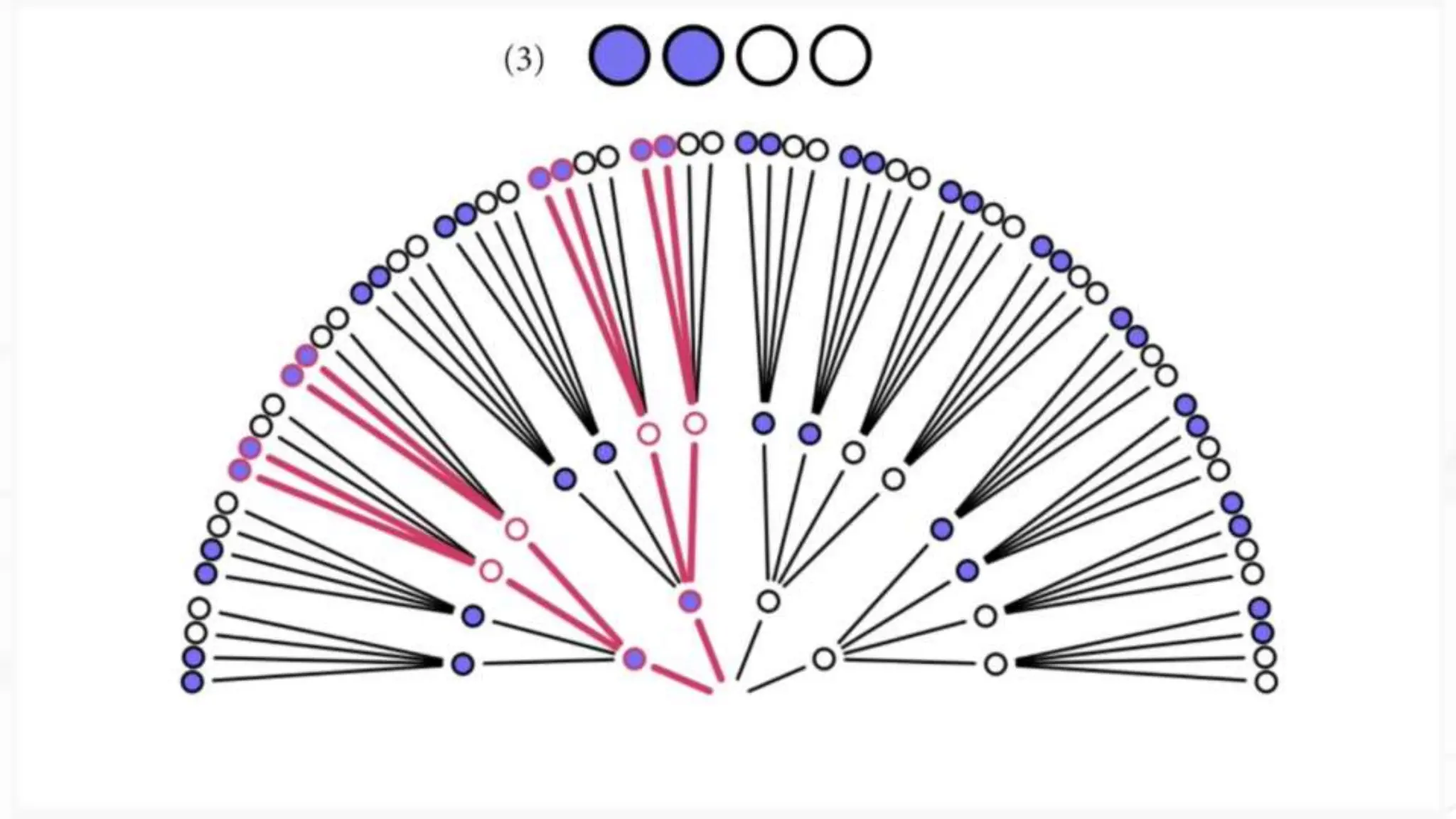
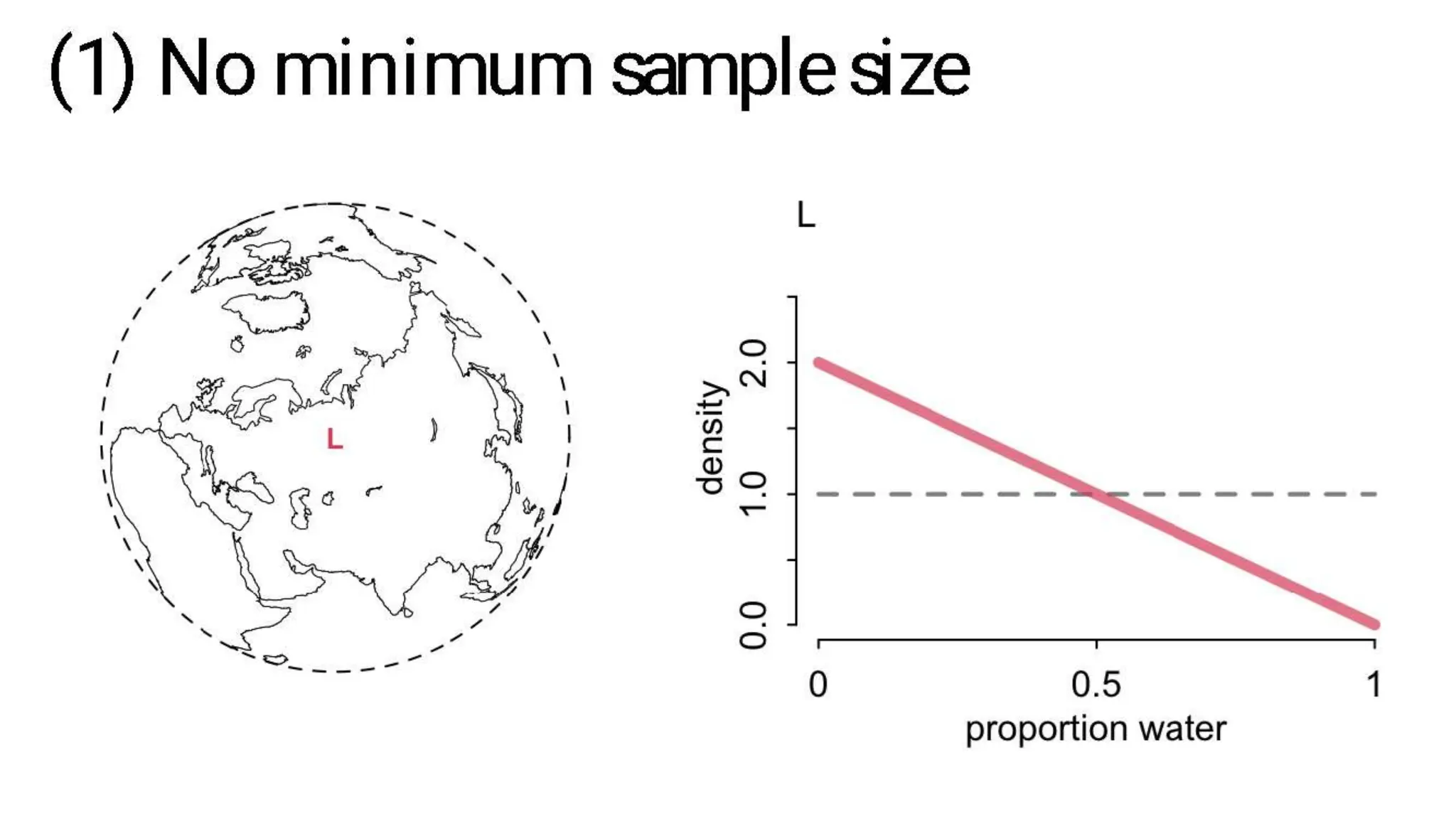
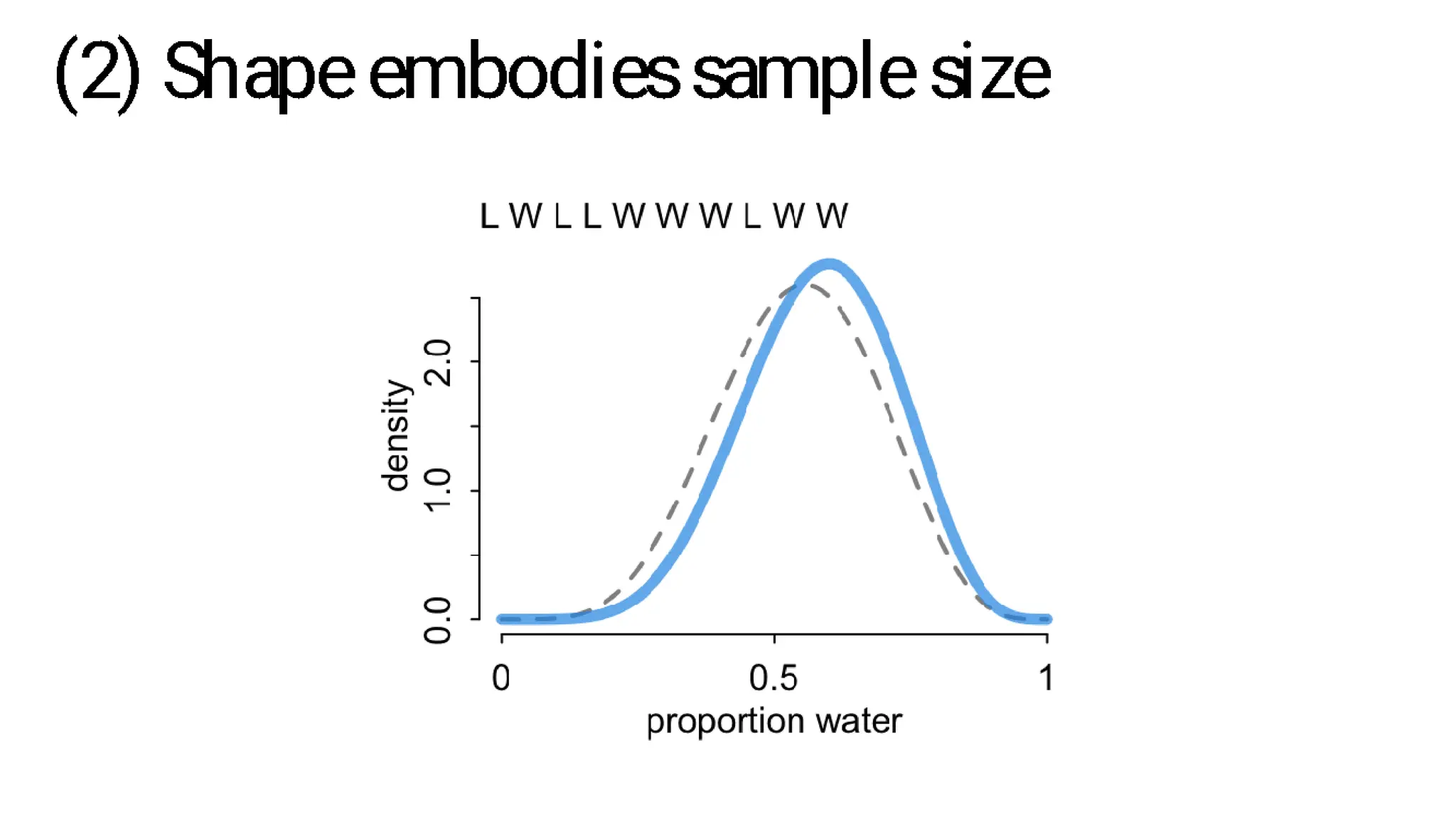
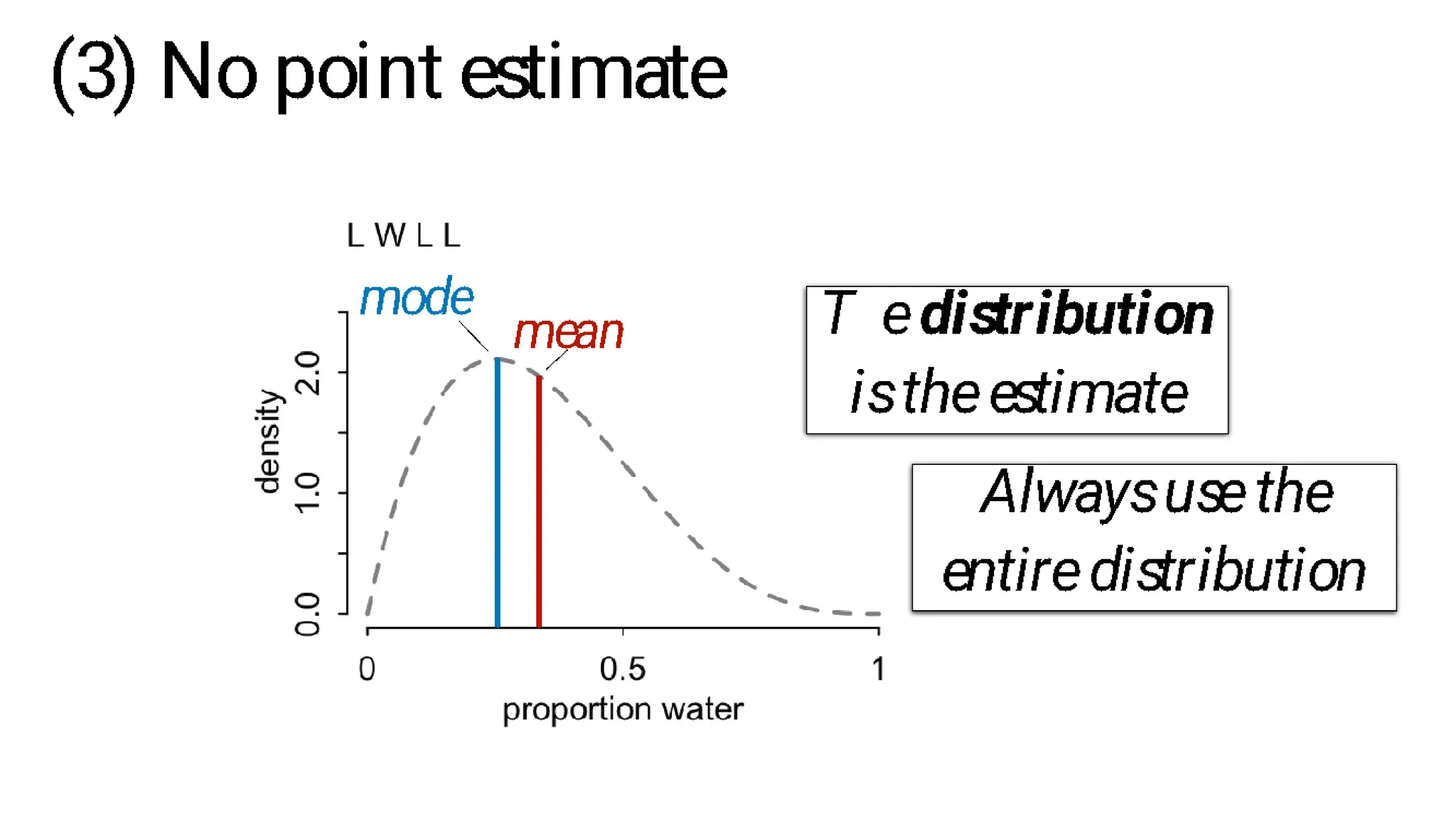
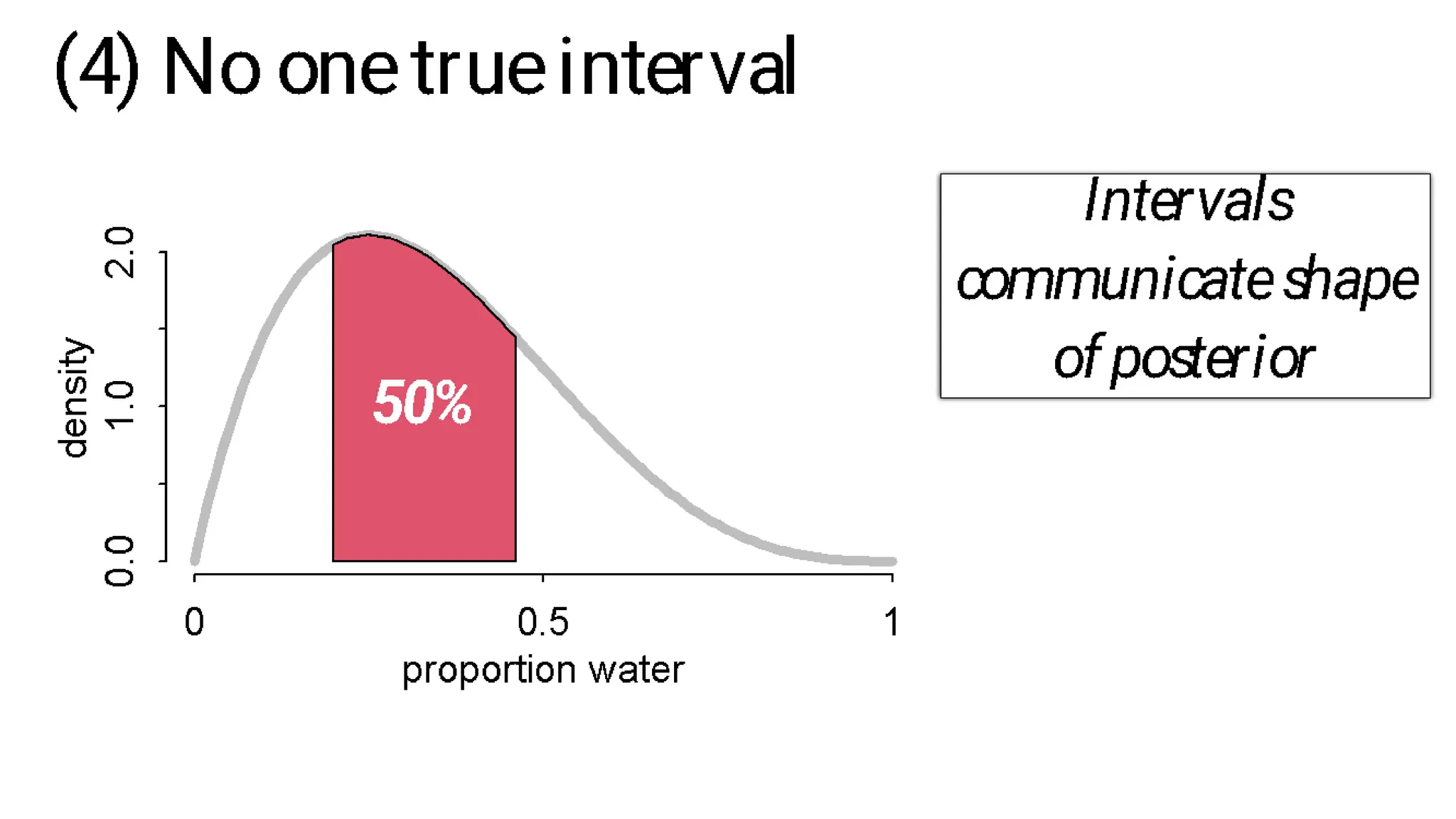
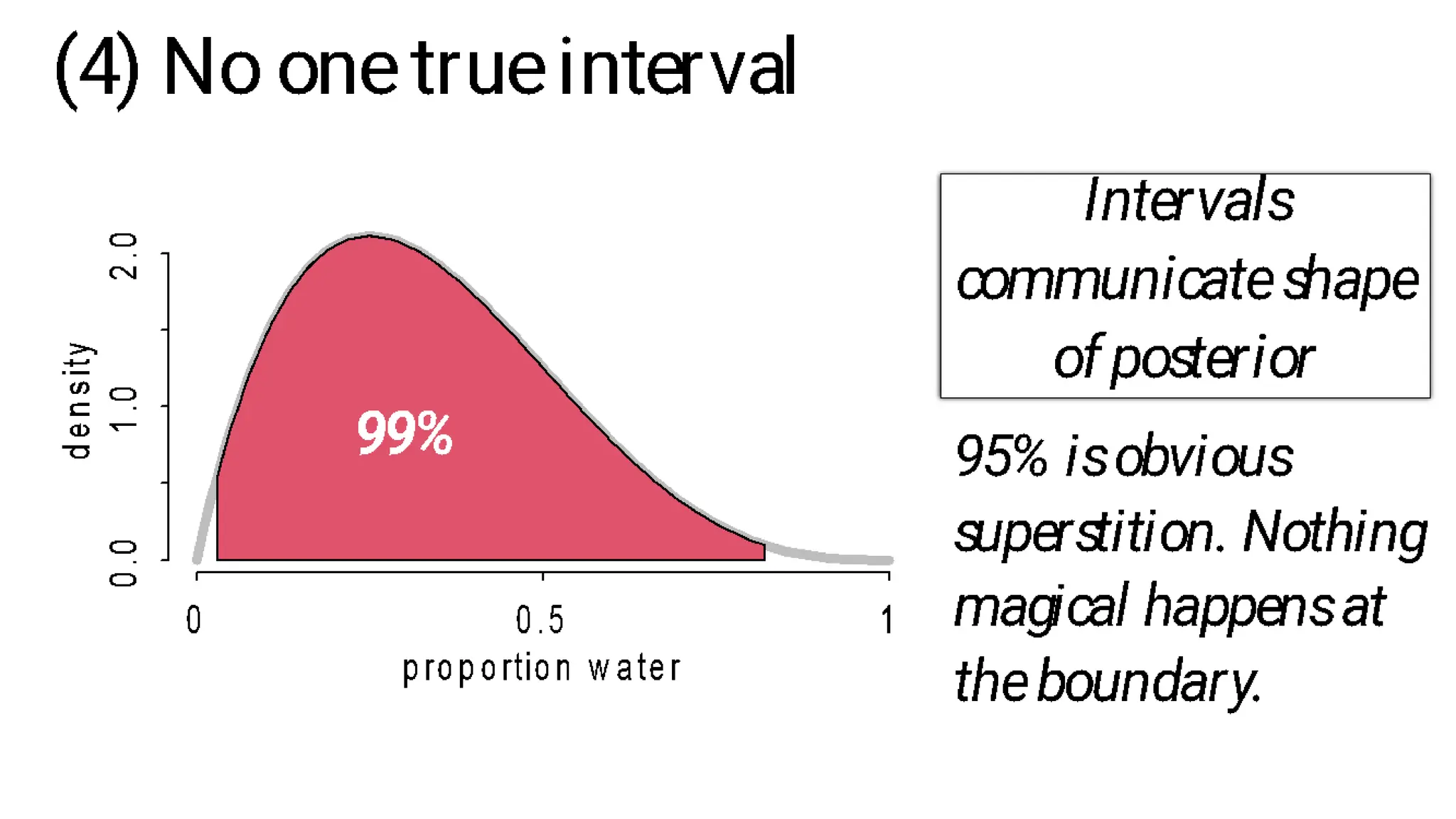
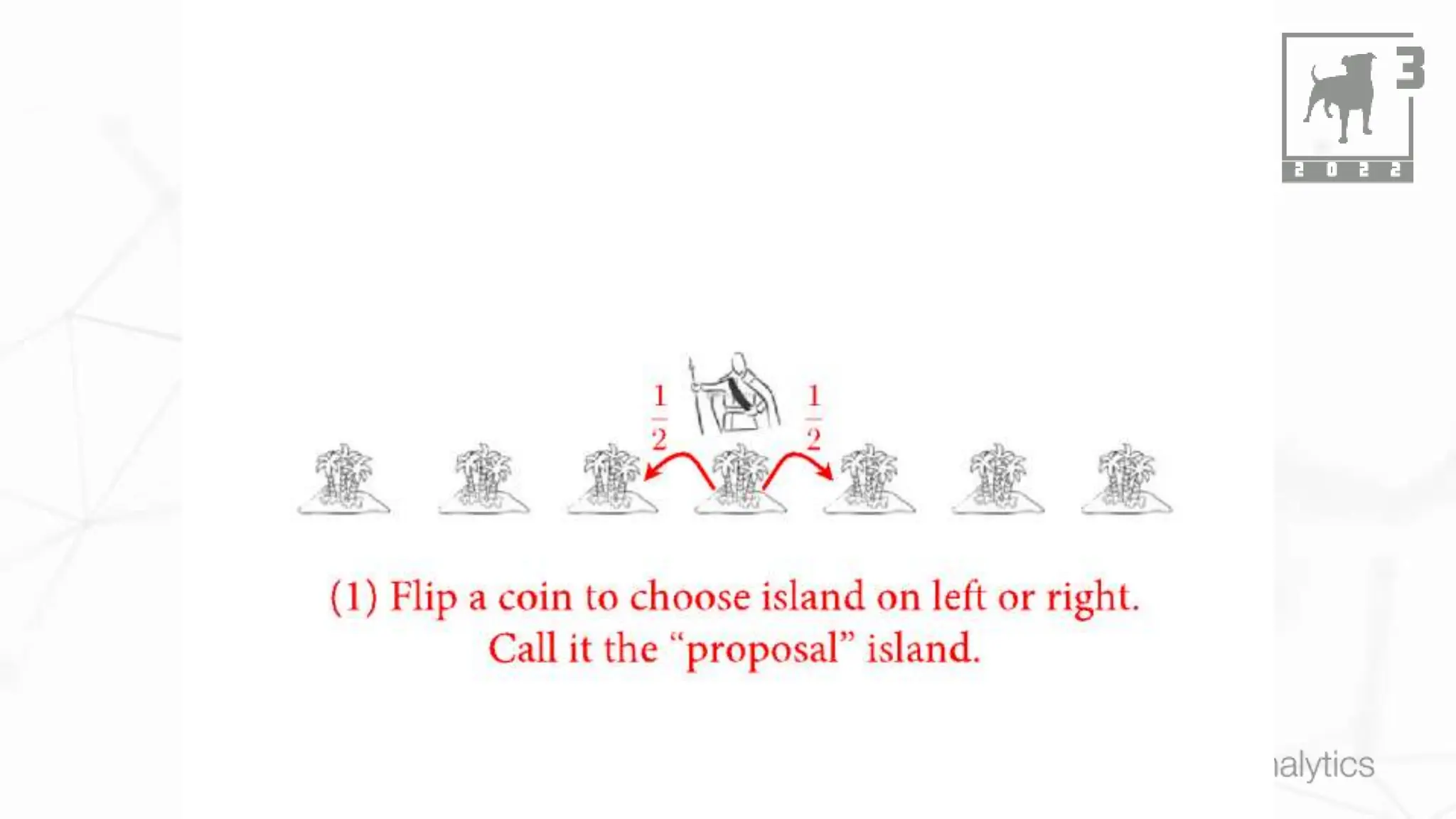
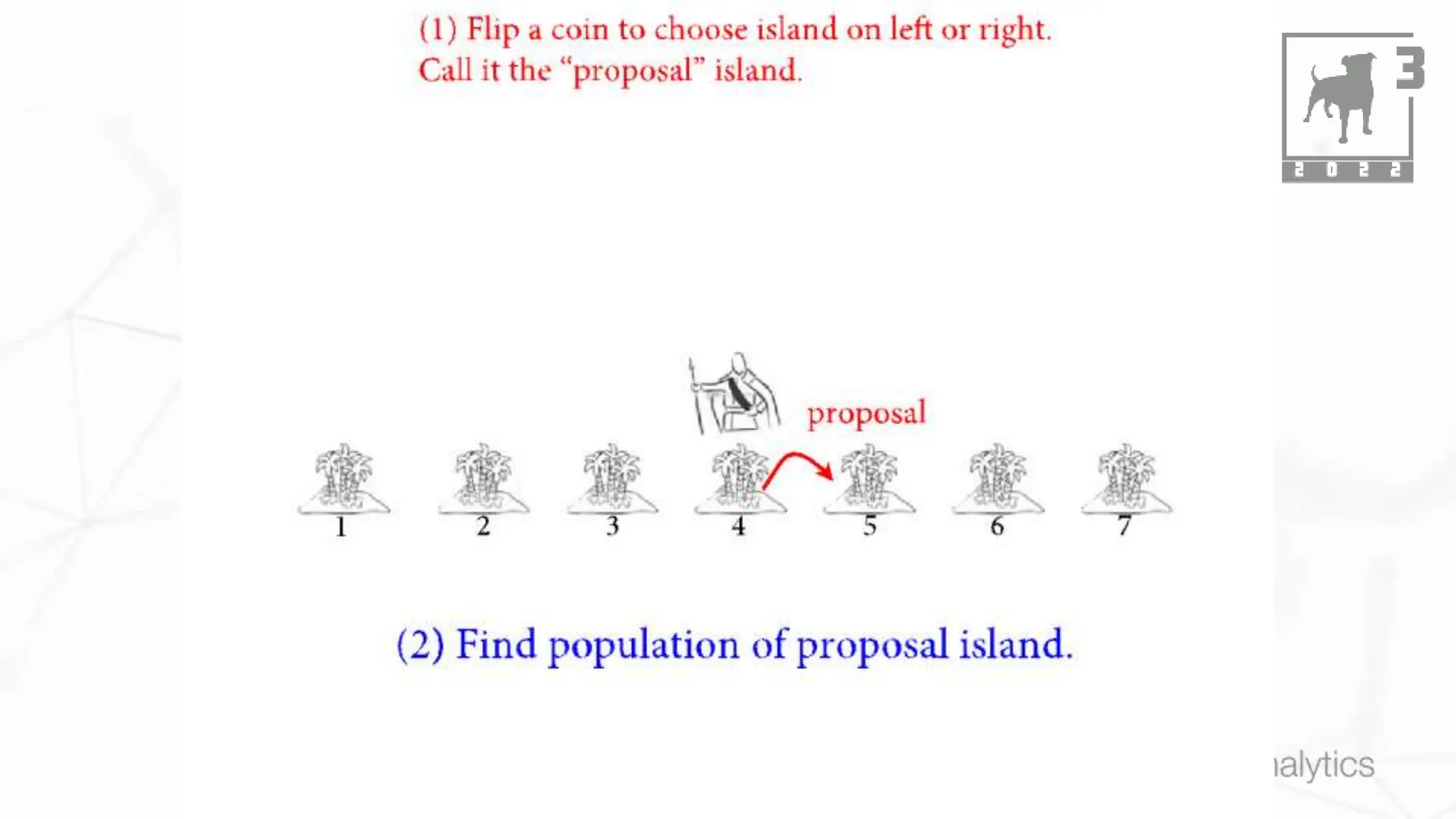
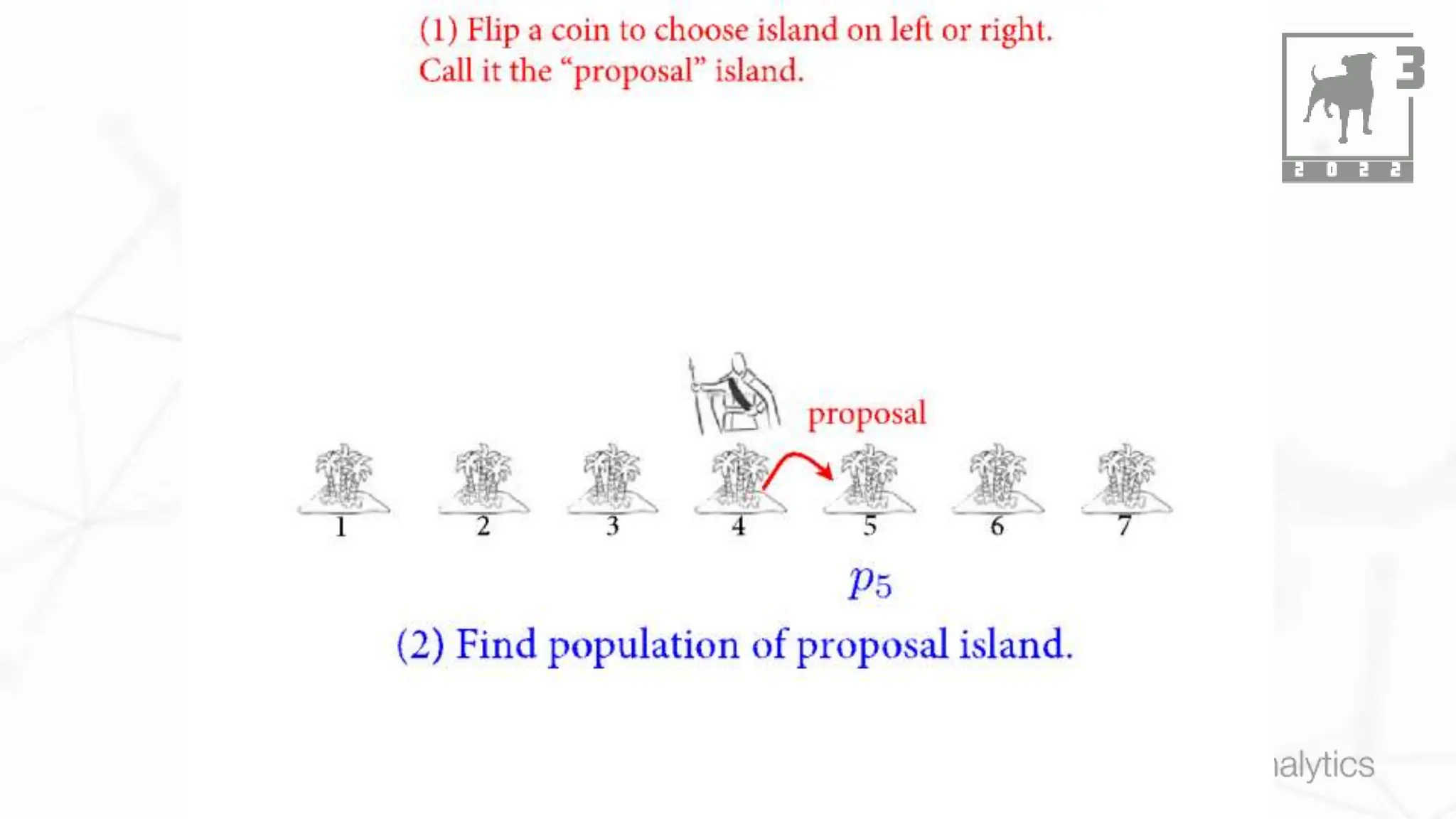
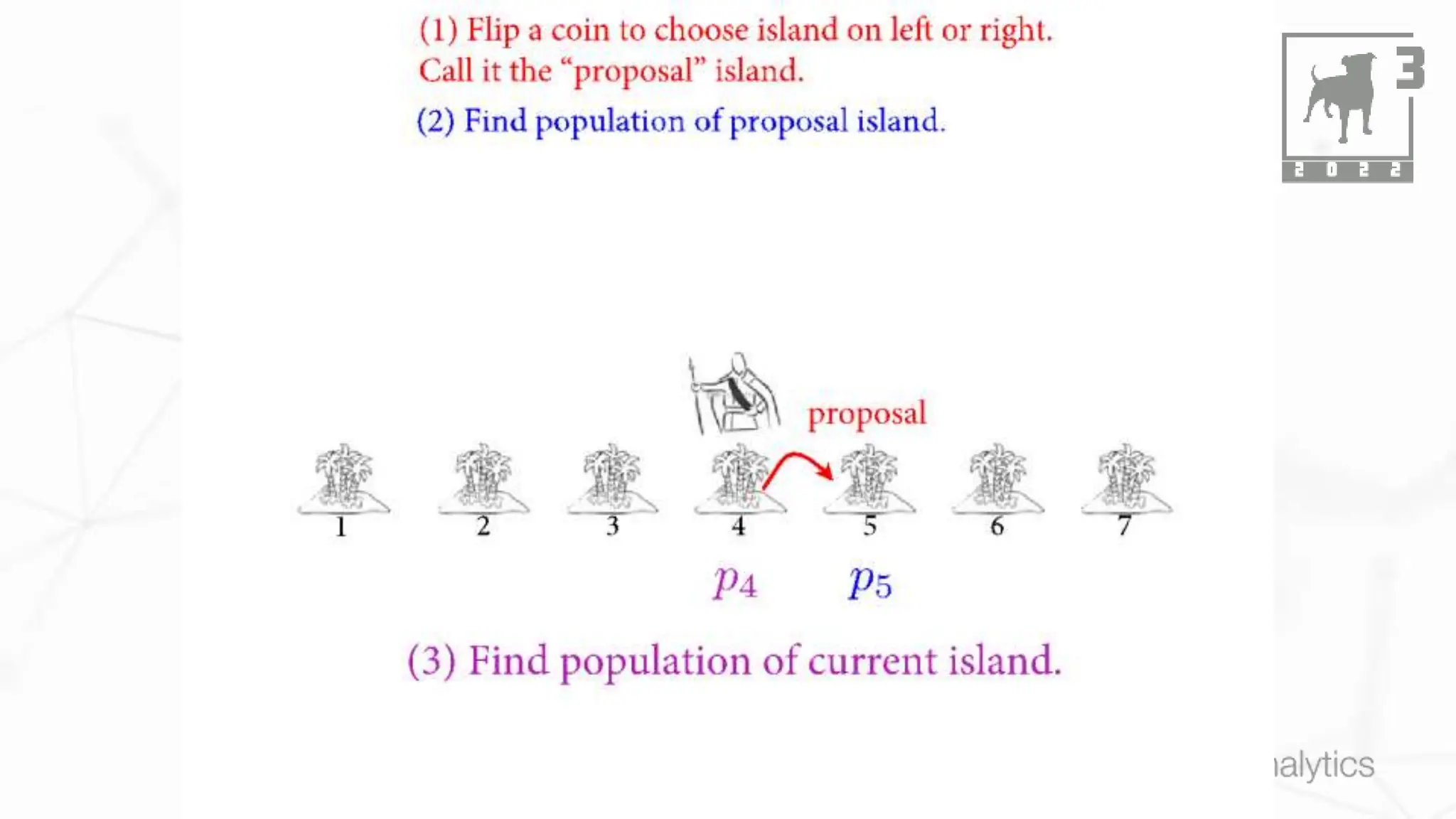
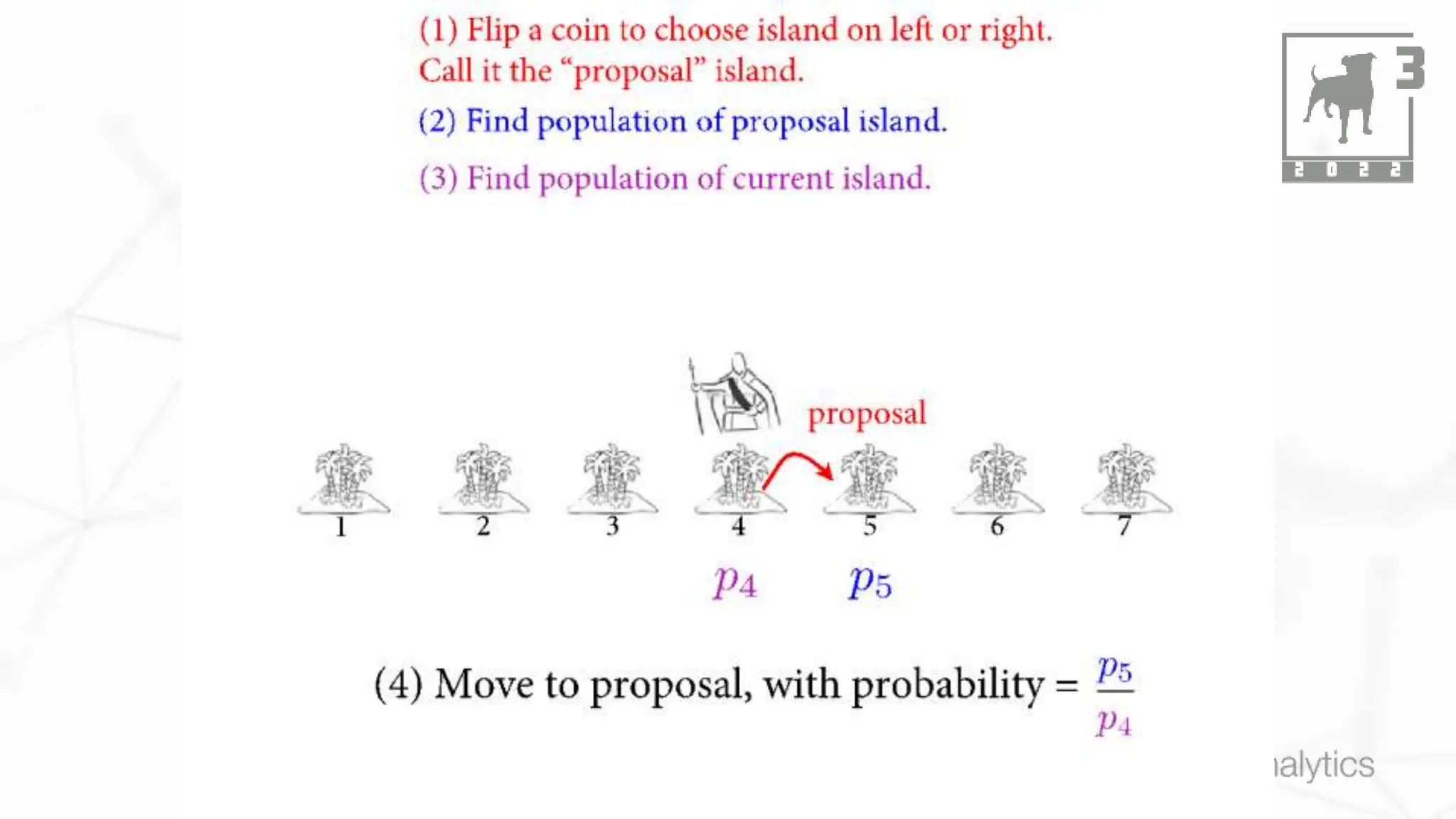
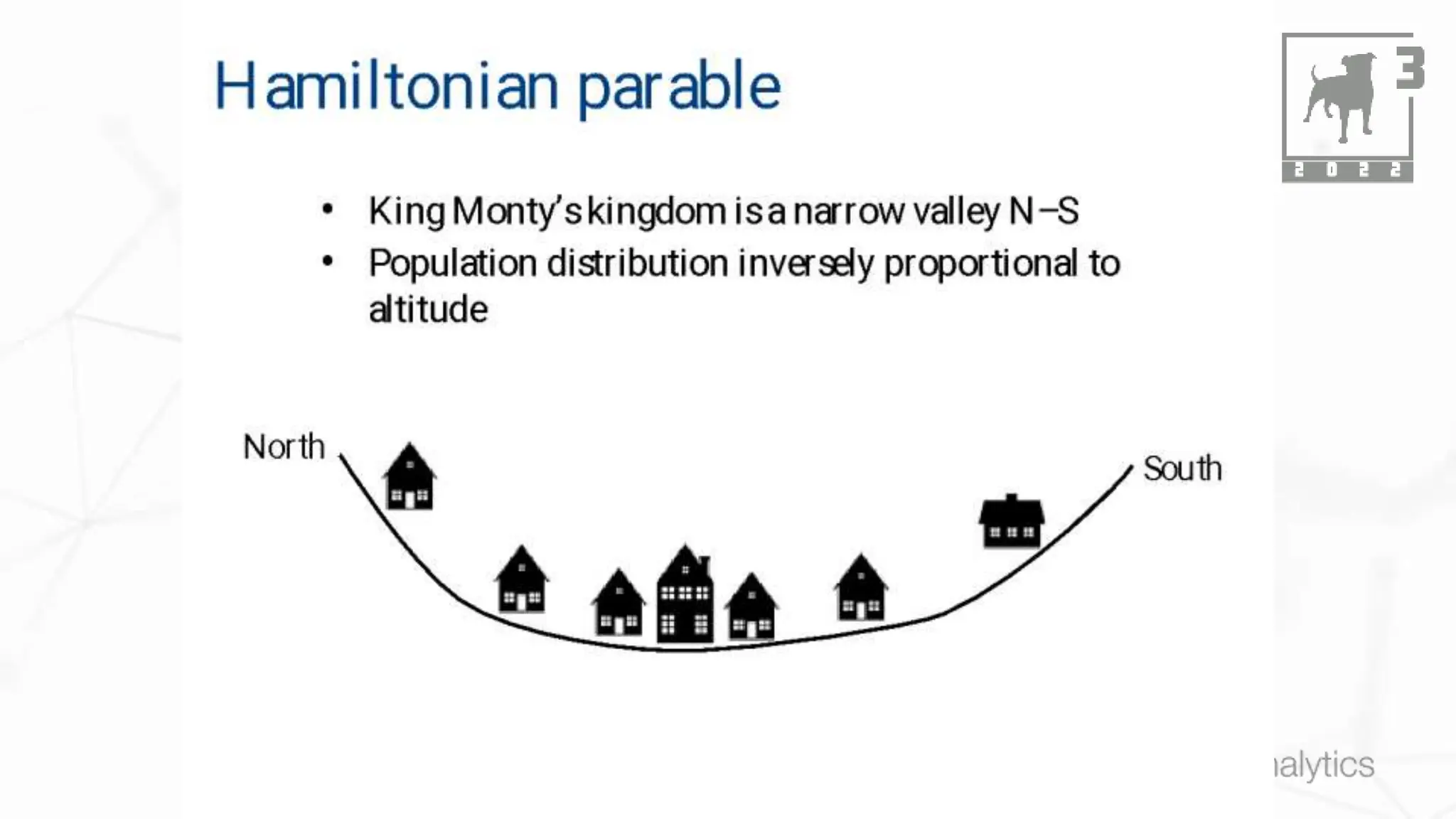
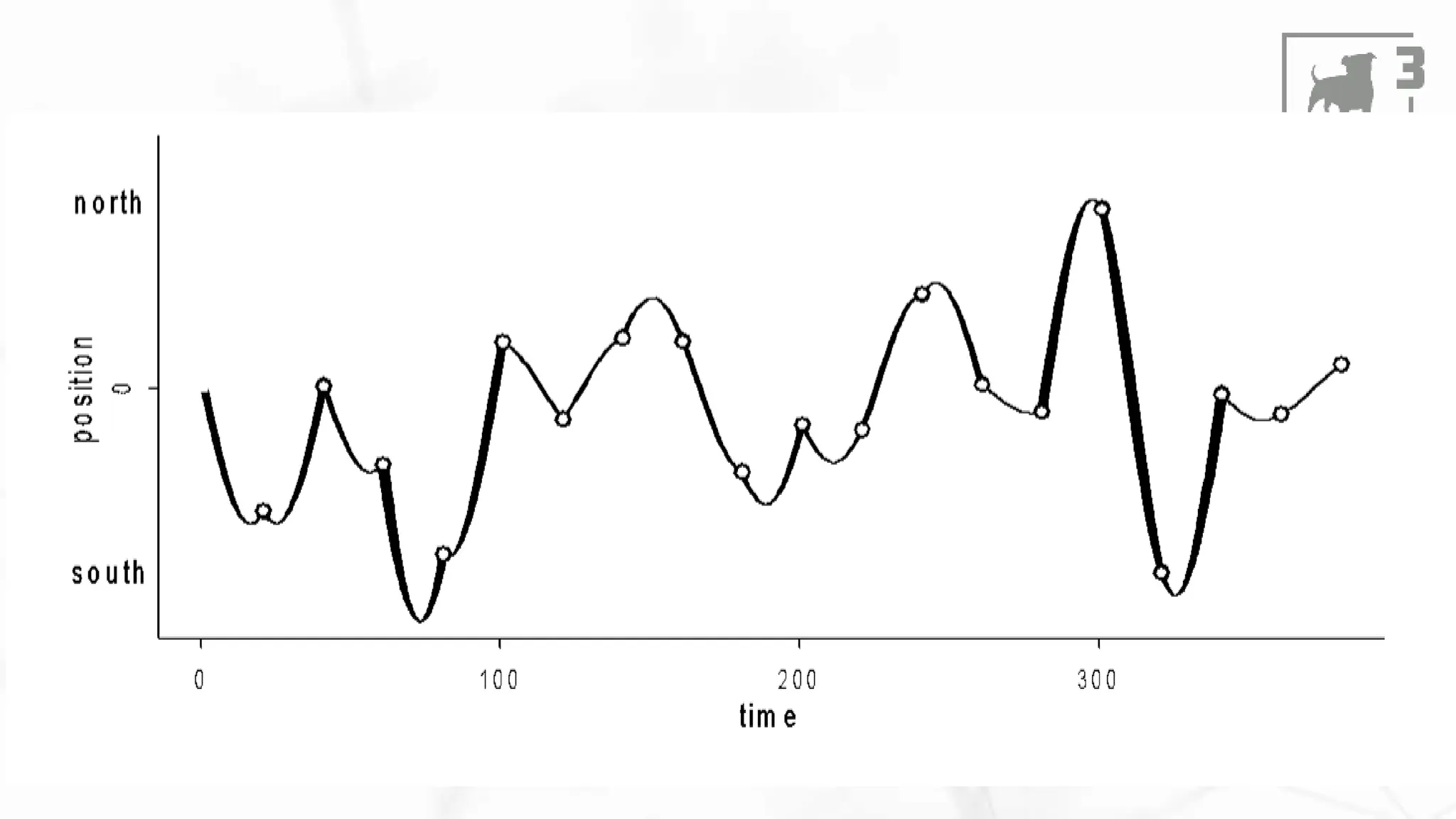
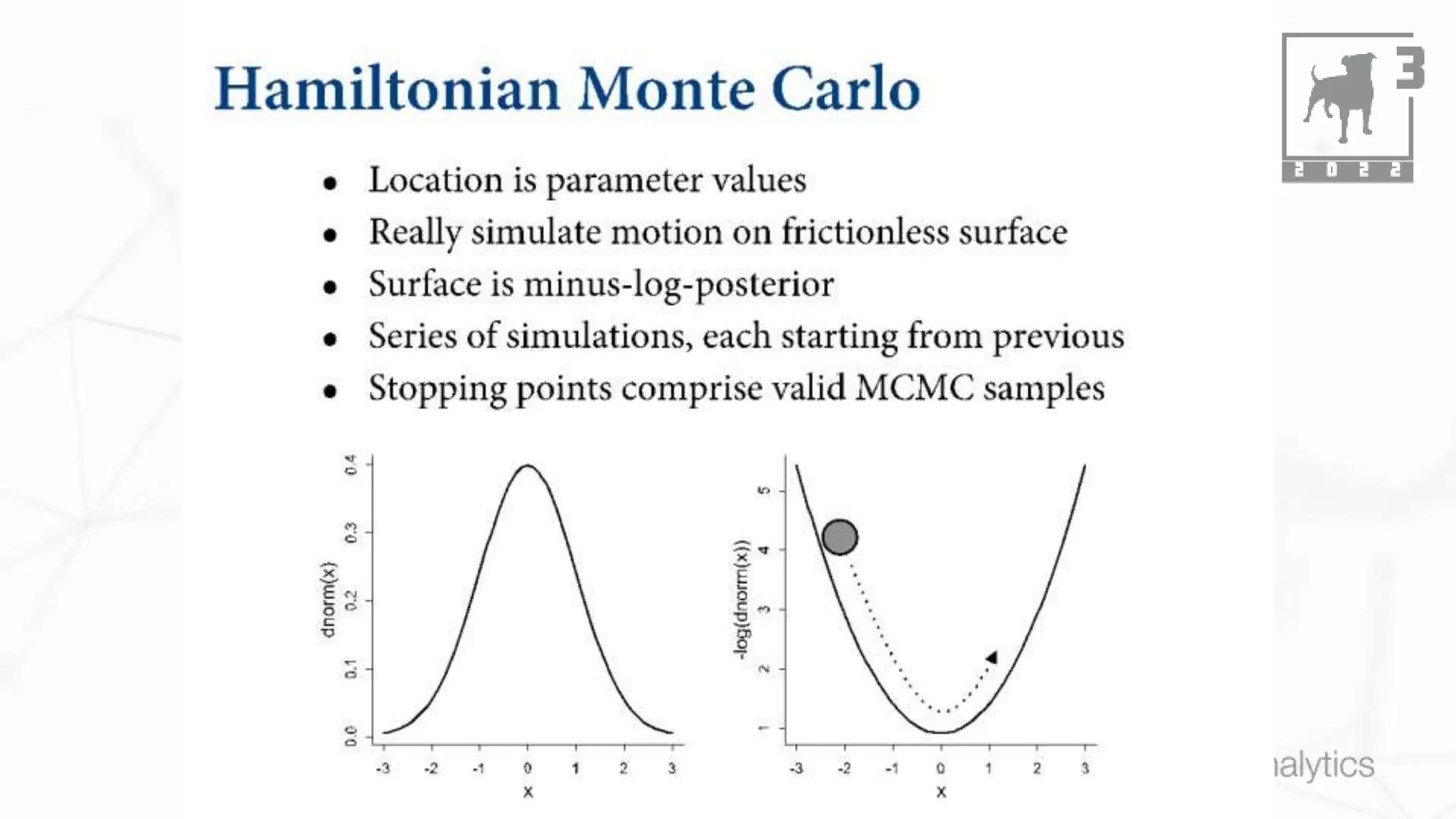
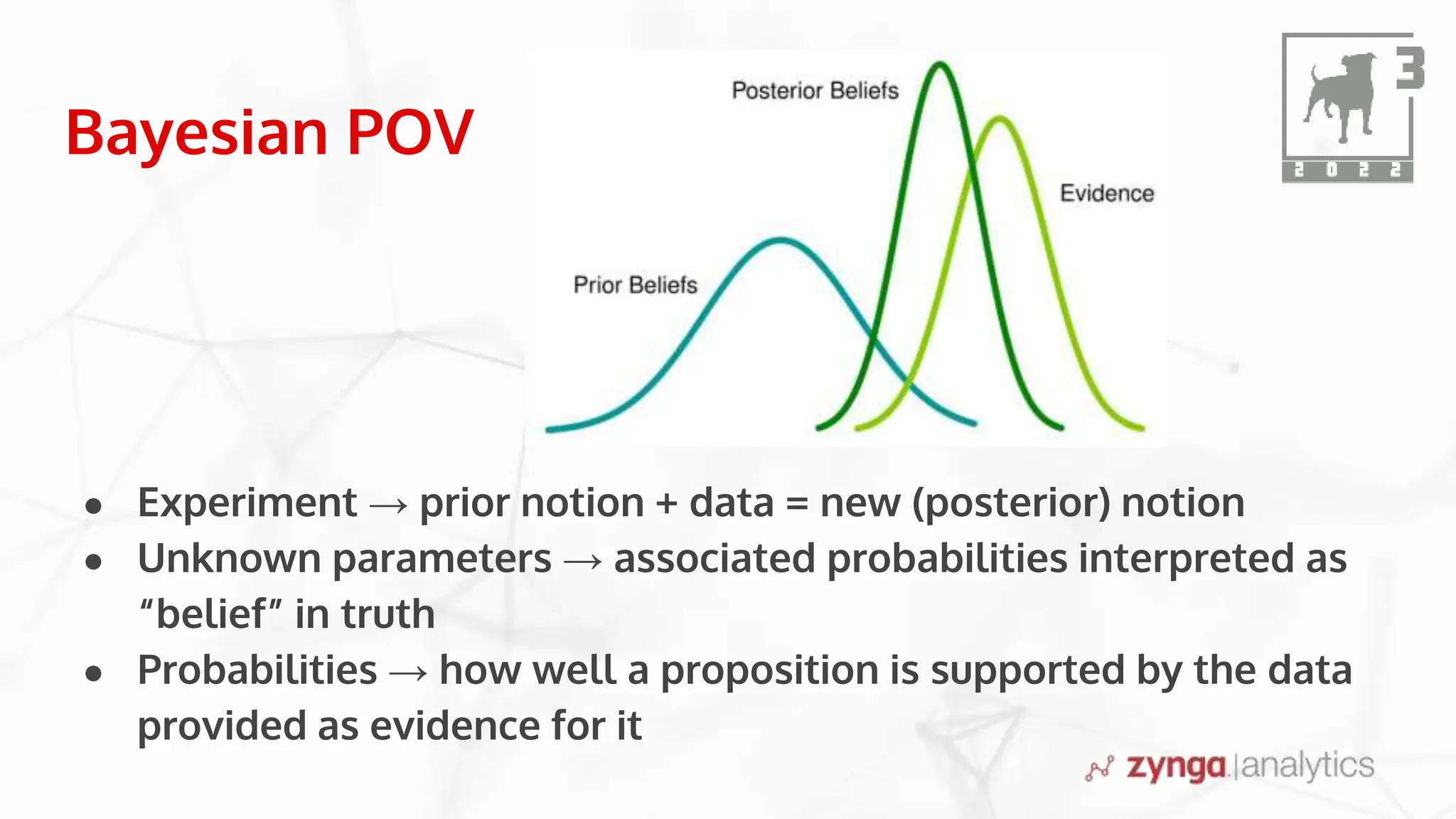
This document discusses Bayesian statistics and its applications. It begins with an overview of Bayes' Theorem and how it allows updating beliefs by counting possibilities in a fancy way. Several examples are then provided of how Bayesian methods can be used, including for A/B testing, modeling, and health monitoring. The document dives deeper into Bayes' Theorem, providing mathematical explanations and walking through an example of estimating the likelihood of a person being a librarian vs. farmer. It emphasizes that Bayesian statistics involves making models, counting outcomes, and updating relative plausibilities based on data.