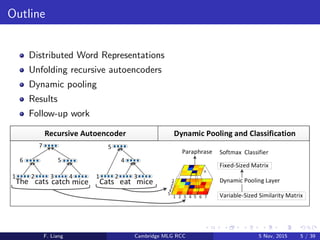
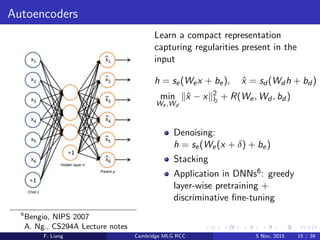
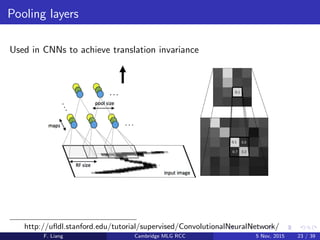
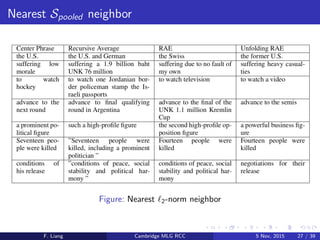
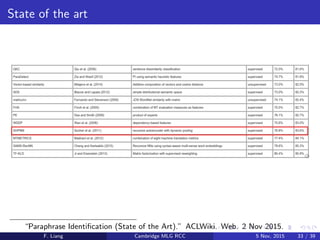
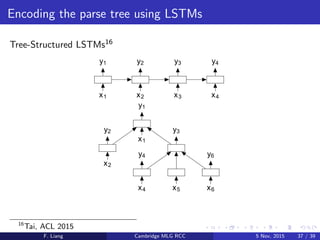
This document discusses paraphrase detection using recursive autoencoders within the realm of machine learning, highlighting the methods used to classify whether two sentences are paraphrases. It covers techniques such as distributed word representations, dynamic pooling, and the architectural details of recursive autoencoders for sentence embedding. Additionally, it presents results from experiments on paraphrase detection tasks with notable accuracy rates and outlines future directions for this research area.

1. Detecting Paraphrases Using Recursive Autoencoders 1
Machine Learning Group RCC
University of Cambridge
Feynman Liang
5 Nov, 2015
1
Socher et al., Dynamic Pooling and Unfolding Recursive Autoencoders for
Paraphrase Detection (NIPS 2011)
F. Liang Cambridge MLG RCC 5 Nov, 2015 1 / 39

2. Example
The judge also refused to postpone the trial date of Sept. 29.
Obus also denied a defense motion to postpone the September trial
date.
F. Liang Cambridge MLG RCC 5 Nov, 2015 2 / 39

3. Paraphrase detection problem
Given: Sentences v1:m, w1:n ∈ V∗
Task: Classify whether v1:m and w1:n are paraphrases of each other
F. Liang Cambridge MLG RCC 5 Nov, 2015 3 / 39

4. Applications
Plagarism Detection
Text Summarization
Information Retrieval
Re-examining Machine Translation Metrics for Paraphrase Identif cation
Nitin Madnani Joel Tetreault
Educational Testing Service
Princeton, NJ, USA
{ nmadnani,jtetreault} @ets.org
F. Liang Cambridge MLG RCC 5 Nov, 2015 4 / 39

5. Outline
Distributed Word Representations
Unfolding recursive autoencoders
Dynamic pooling
Results
Follow-up work
F. Liang Cambridge MLG RCC 5 Nov, 2015 5 / 39

6. Distributed word representations
F. Liang Cambridge MLG RCC 5 Nov, 2015 6 / 39

7. Distributional semantics
Goal: Construct a represenation for language which captures semantic
meaning and is convenient for computation
From linguistics:
Lexical/compositional semantics: meaning through individual words
and syntactic constructions (WordNet, formal language theory)
Distributional semantics: meaning through statistical properties (large
datasets, linear algebra)
Distributional hypothesis2
: “A word is characterized by the company it
keeps”
One way to do so is to model join density p(w1:T ) for w1:T ∈ V∗
2
Firth, Studies in Linguistic Analysis 1957
F. Liang Cambridge MLG RCC 5 Nov, 2015 7 / 39

8. Curse of dimensionality
English language actually has > 106 words, but for simplicity’s sake:
|V| = 105
, w1:10 ∈ V∗
How many free parameters could we potentially need to represent
p(w1:10)?
F. Liang Cambridge MLG RCC 5 Nov, 2015 8 / 39

9. Simplifying assumption
O(|V|n) is intractable.
Dependencies between words tend to exist only within a local context
=⇒ factorization into CPDs:
P(w1:T ) ≈
T
t=1
P(wt|contextt ⊂ w1:t−1wt+1:n)
For example:
n-gram: context = wi−n+1:i−1
Continuous Bag of Words (word2vec)3: context = wi−4:i+4
3
Mikolov, ICLR 2013
F. Liang Cambridge MLG RCC 5 Nov, 2015 9 / 39

10. Distributed representation for words
From Bengio, JMLR 2003:
1 Associate with each word in the vocabulary a distributed
word feature vector (w ∈ RD)
2 Express the joint probability function of word sequences in
terms of the feature vectors of these words in the sequence,
and
3 Learn simultaneously the word feature vectors and the
parameters of that probability function
Embedding Matrix Le : V → RD
Joint PDF P(w1:T )
P(w1:T ) =
T
t=1
P(wt|Le(wt−n+1:t−1))
What are we taking the context to be? How many parameters does
P(w1:T ) have?
F. Liang Cambridge MLG RCC 5 Nov, 2015 10 / 39

11. Neural-network parameterization of CPD
Number free parameters ∈ O(n + D|V|)
J (θ) = 1
T t [− log P(wt|Le(wt−n+1:t−1), θ)] + R(θ)
Bengio, JMLR 2003
F. Liang Cambridge MLG RCC 5 Nov, 2015 11 / 39

12. A “semantic” vector space
Empirically5:
Words with similar meaning are mapped close together
Directions in the vector space correspond to semantic concepts
Figure: “gender” and “singular/plural” vector offsets from word analogy task
5
Mikolov, NAACL 2013
F. Liang Cambridge MLG RCC 5 Nov, 2015 12 / 39

13. Unfolding Recursive Autoencoders
F. Liang Cambridge MLG RCC 5 Nov, 2015 13 / 39

14. From words to sentences
Le : V → RD embeds words into a semantic vector space where the metric
approximates semantic similarity.
If instead we had a V∗ → RD for sentences, then we can measure sentence
similarity and detect paraphrases. . .
F. Liang Cambridge MLG RCC 5 Nov, 2015 14 / 39

15. Autoencoders
Learn a compact representation
capturing regularities present in the
input
h = se(Wex + be), ˆx = sd (Wd h + bd )
min
We ,Wd
ˆx − x 2
l2
+ R(We, Wd , bd )
Denoising:
h = se(We(x + δ) + be)
Stacking
Application in DNNs6: greedy
layer-wise pretraining +
discriminative fine-tuning
6
Bengio, NIPS 2007
A. Ng., CS294A Lecture notes
F. Liang Cambridge MLG RCC 5 Nov, 2015 15 / 39

16. Recursive autoencoders for sentence embedding
(RD)∗ → RD: recursively apply RD × RD → RD
yi = f (We[xj ; xk] + b)
f , activation function
Free parameters:
We ∈ RD×2D
, encoding matrix
b ∈ RD
, bias
Anything missing from this definition?
F. Liang Cambridge MLG RCC 5 Nov, 2015 16 / 39

17. Associativity
Associativity of the binary operation is provided by a grammatical parse
tree (e.g. obtained from CoreNLP8):
8
Klein (ACL 2003)
F. Liang Cambridge MLG RCC 5 Nov, 2015 17 / 39

18. Training recursive autoencoders
Wd “undoes” We (minimizes square reconstruction error)
To train:
argminWe ,Wd
[x1; y1] − [x1; y1] 2
2
+ R(We, Wd )
Notice anything asymmetrical? (hint: is this even an autoencoder?)
F. Liang Cambridge MLG RCC 5 Nov, 2015 18 / 39

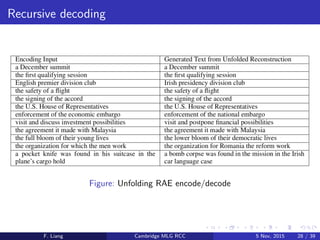
19. Unfolding RAEs
Reconstruction error was only measured against a single decoding step!
Instead, recursively apply Wd to decode down to terminals
argminWe ,Wd
[xi ; . . . ; xj ] − [xi ; . . . ; xj ] 2
2
+ R(We, Wd )
Children with larger subtrees weighted more
DAG =⇒ efficiently optimized via back-propogation through
structure9 and L-BFGS
9
Goller, 1995
F. Liang Cambridge MLG RCC 5 Nov, 2015 19 / 39

20. Dynamic pooling
F. Liang Cambridge MLG RCC 5 Nov, 2015 20 / 39

21. Measuring sentence similarity
From sentence x1:N and RAE encoding y1:K , form
s = [x1, . . . , xN, y1, . . . , yK ]
For two sentences s1, s2, the similarity matrix S has entries
(S)i,j = (s1)i − (s2)j
2
2
F. Liang Cambridge MLG RCC 5 Nov, 2015 21 / 39

22. Handling varying sentence length
Sentence lengths may vary =⇒ S dimensionality may vary.
Would like S → Spooled ∈ Rnp×np with np constant.
F. Liang Cambridge MLG RCC 5 Nov, 2015 22 / 39

23. Pooling layers
Used in CNNs to achieve translation invariance
http://ufldl.stanford.edu/tutorial/supervised/ConvolutionalNeuralNetwork/
F. Liang Cambridge MLG RCC 5 Nov, 2015 23 / 39

24. Dynamic pooling of the similarity matrix
Dynamically partition rows and columns of S into np equal parts
Min. pool (why?) over each part
Normalize µ = 0, σ = 1 and pass on to classifier
F. Liang Cambridge MLG RCC 5 Nov, 2015 24 / 39

25. Results
F. Liang Cambridge MLG RCC 5 Nov, 2015 25 / 39

26. Qualitative evaluation of unsupervised feature learning
Dataset
150,000 sentences from NYT and AP sections of Gigaword corpus for
RAE training
Setup
R100 off-the-shelf feature vectors for word embeddings11
Stanford parser12 to extract parse tree
Baseline
Recursive average of all word vectors in parse tree
11
Turian, ACL 2010
12
Klein, ACL 2003
F. Liang Cambridge MLG RCC 5 Nov, 2015 26 / 39

27. Nearest Spooled neighbor
Figure: Nearest 2-norm neighbor
F. Liang Cambridge MLG RCC 5 Nov, 2015 27 / 39

28. Recursive decoding
Figure: Unfolding RAE encode/decode
F. Liang Cambridge MLG RCC 5 Nov, 2015 28 / 39

29. Paraphrase detection task
Dataset
Microsoft Research paraphrase corpus (MSRP)13
5,801 sentence pairs, 3,900 labeled as paraphrases
13
Dolan, COLING 2004
F. Liang Cambridge MLG RCC 5 Nov, 2015 29 / 39

30. Paraphrase detection task
Setup
4,076 training pairs (67.5% positive), 1,725 test pairs (66.5%
positive)
∀(S1, S2) ∈ D, (S2, S1) also added
Add features ∈ {0, 1} to Spooled related to the set of numbers in S1
and S2
Numbers in S1 = numbers in S2
(Numbers in S1 ∪ numbers in S2) = ∅
Numbers in one sentence ⊂ numbers in other
Softmax classifier over Spooled
F. Liang Cambridge MLG RCC 5 Nov, 2015 30 / 39

31. Example results
F. Liang Cambridge MLG RCC 5 Nov, 2015 31 / 39

32. Numerical results
Recursive averaging: 75.9%
Standard RAE: 75.5%
Unfolding RAE: 76.8%
F. Liang Cambridge MLG RCC 5 Nov, 2015 32 / 39

33. State of the art
“Paraphrase Identification (State of the Art).” ACLWiki. Web. 2 Nov 2015.
F. Liang Cambridge MLG RCC 5 Nov, 2015 33 / 39

34. Does the dynamic pooling layer add anything?
S-histogram 73.0%
Only added number features 73.2%
Only Spooled 72.6%
Top URAE Node 74.2%
Spooled + number features 76.8%
Is anything suspicious about these results?
F. Liang Cambridge MLG RCC 5 Nov, 2015 34 / 39

35. Follow-Up Work Since 2011
F. Liang Cambridge MLG RCC 5 Nov, 2015 35 / 39

36. Extending RAEs to capture compositionality
Recursive Matrix-Vector Spaces15
p = f We
c1
c2
+ b → p = f We
Ba + b0
Ab + a0
+ p0
15
Socher, EMNLP 2012
F. Liang Cambridge MLG RCC 5 Nov, 2015 36 / 39

37. Encoding the parse tree using LSTMs
Tree-Structured LSTMs16
x1 x2 x3 x4
y1 y2 y3 y4
x1
x2
x4 x5 x6
y1
y2 y3
y4 y6
16
Tai, ACL 2015
F. Liang Cambridge MLG RCC 5 Nov, 2015 37 / 39

38. Different “semantic norms” on the word vector space
Neural Tensor Networks17
g(e1, R, e2) = uT
R f eT
1 W
[1:k]
R e2 + VR
e1
e2
+ bR
Francesco
Guicciardini
historian male
ItalyFlorence
Francesco
Patrizi
Matteo
Rosselli
profession
gender
place of birth
nationality
location nationality
nationality
gender
17
Socher, NIPS 2013
F. Liang Cambridge MLG RCC 5 Nov, 2015 38 / 39

39. Questions?