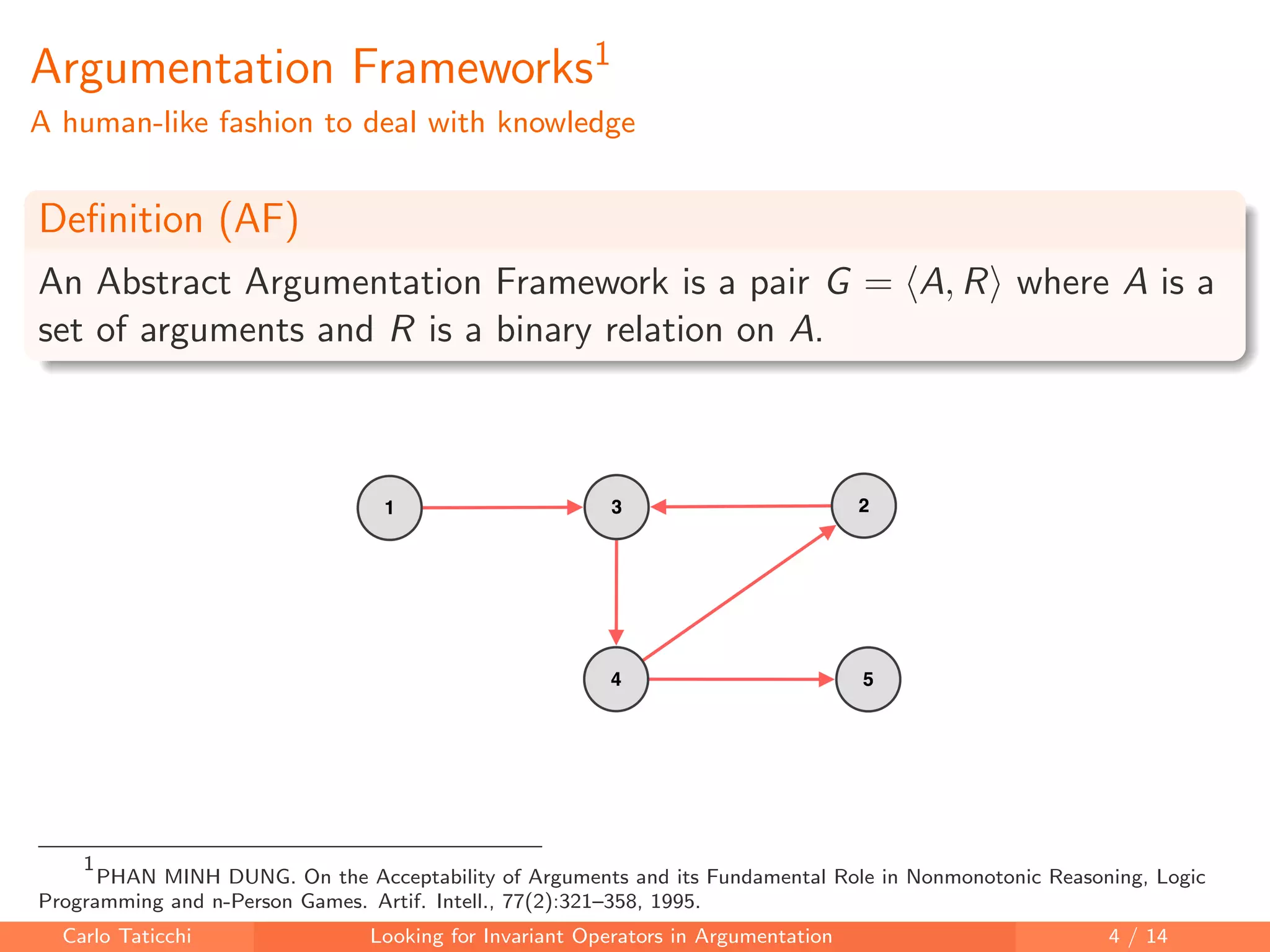
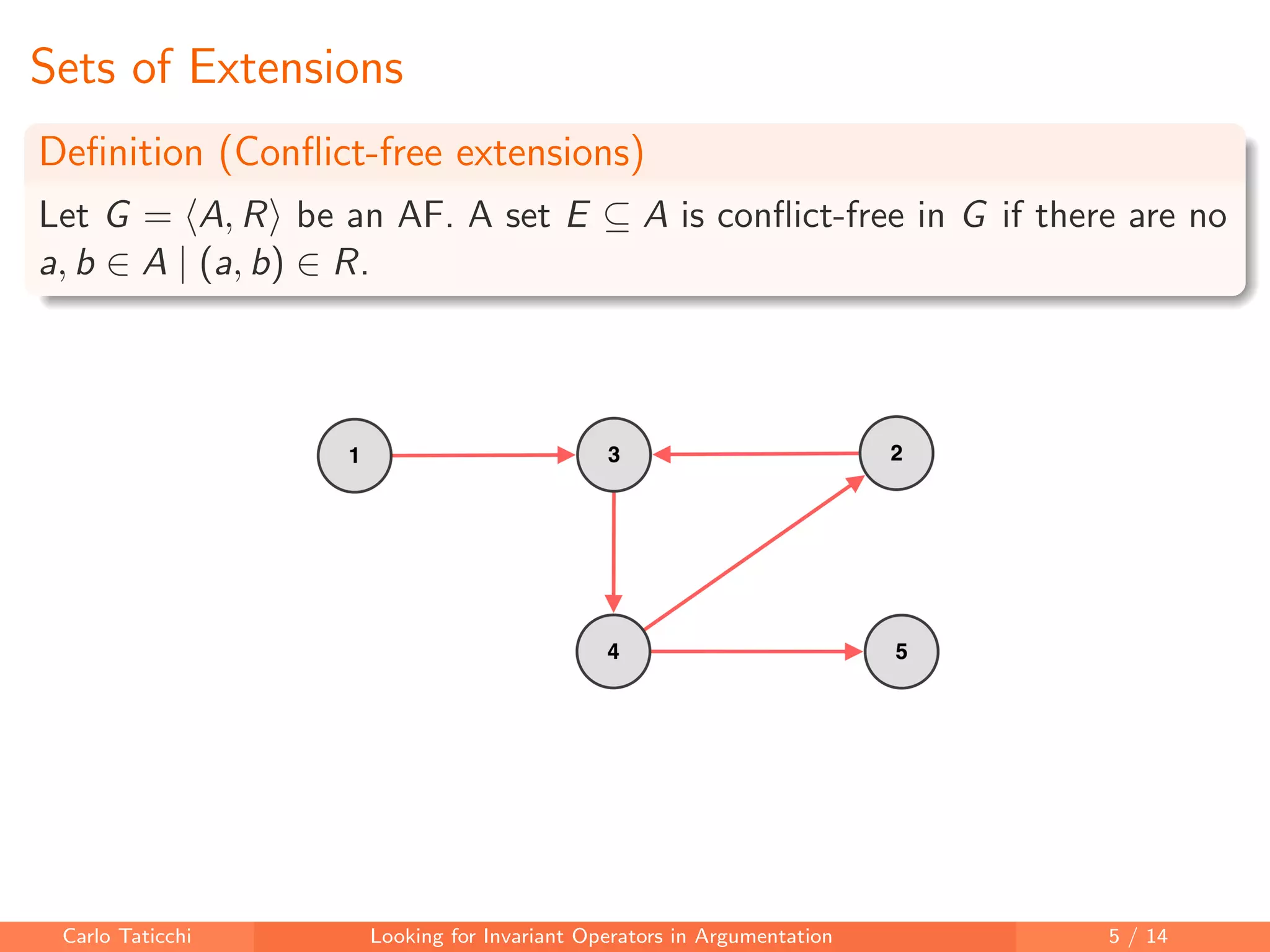
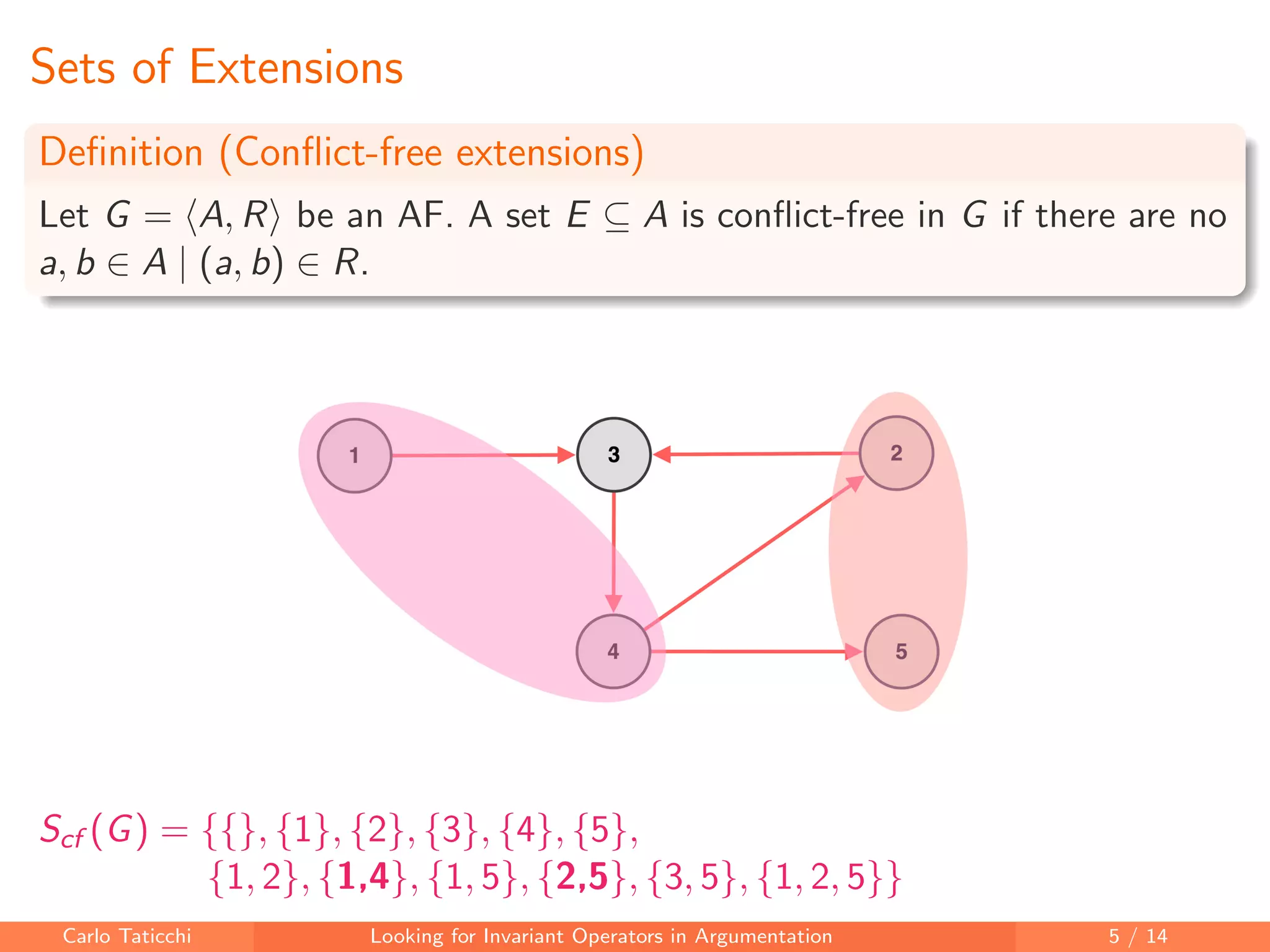
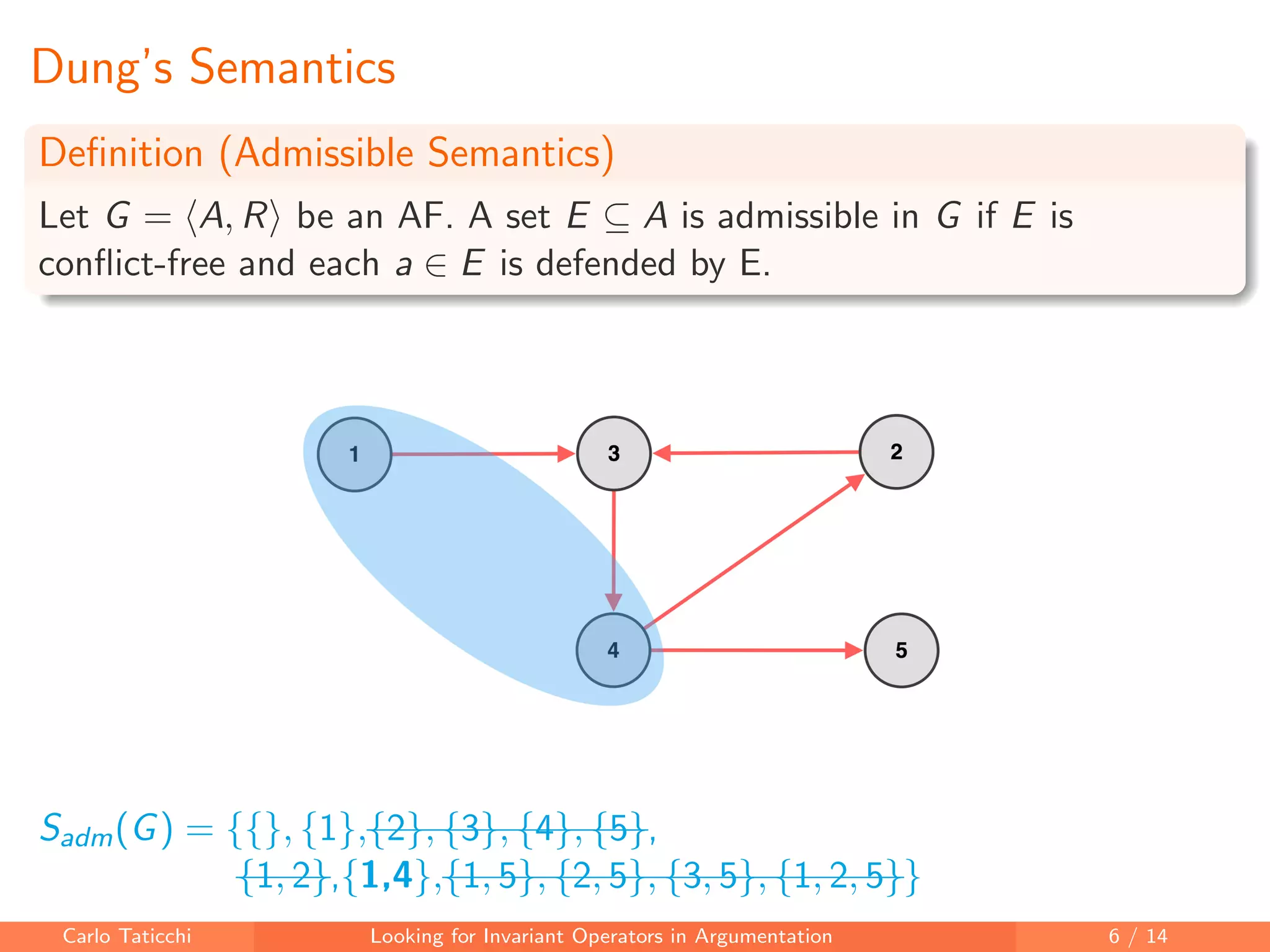
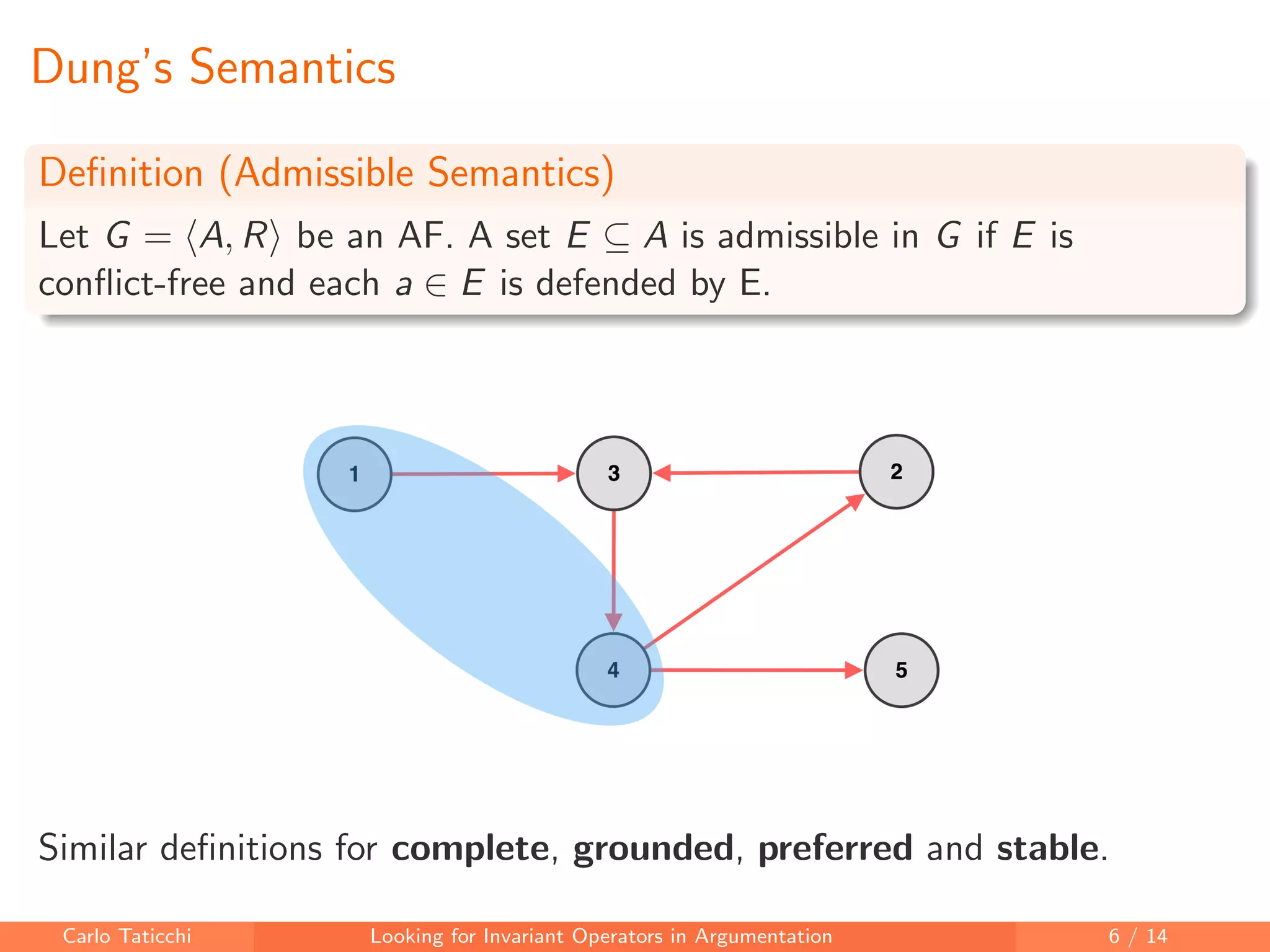
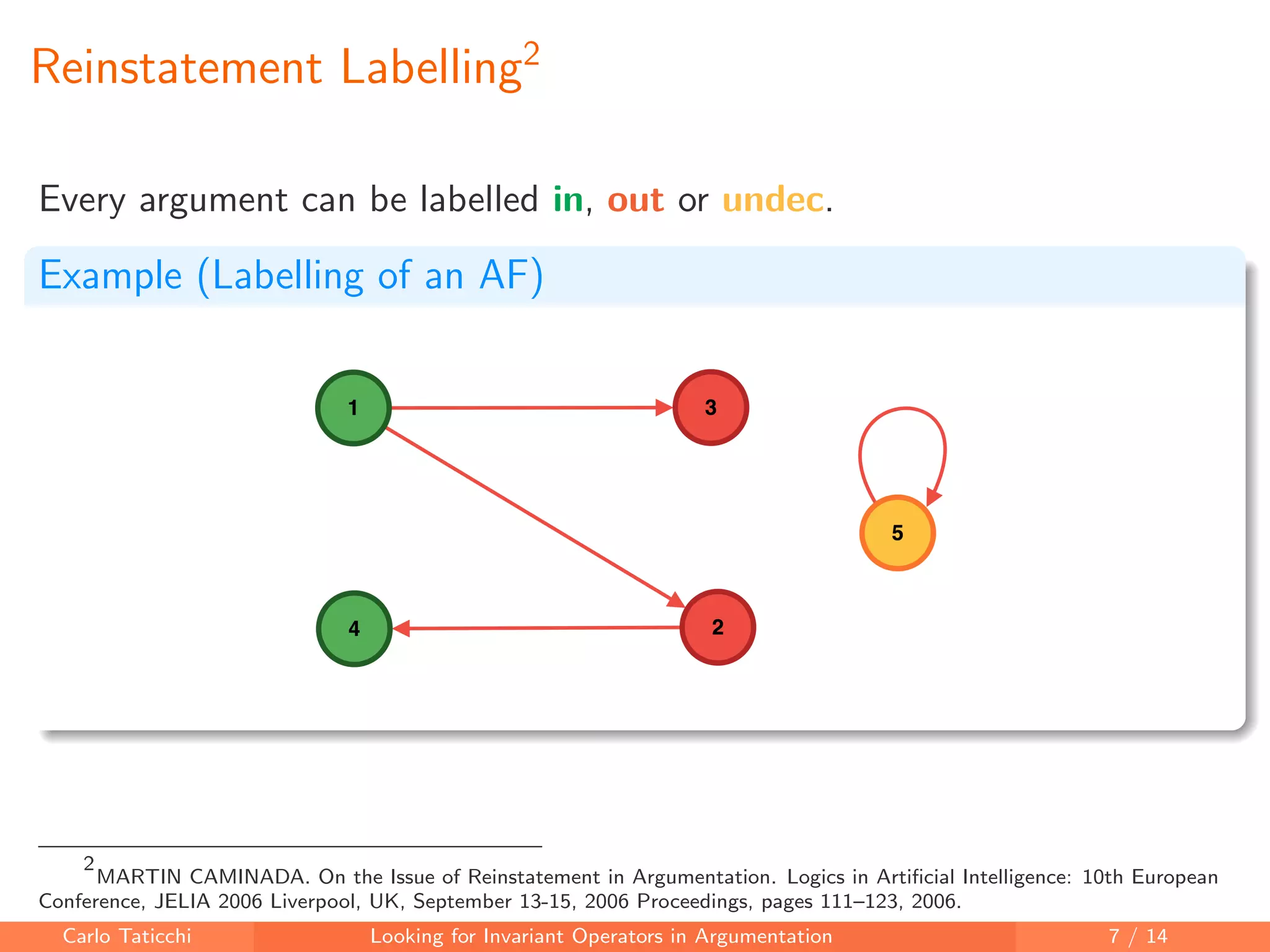
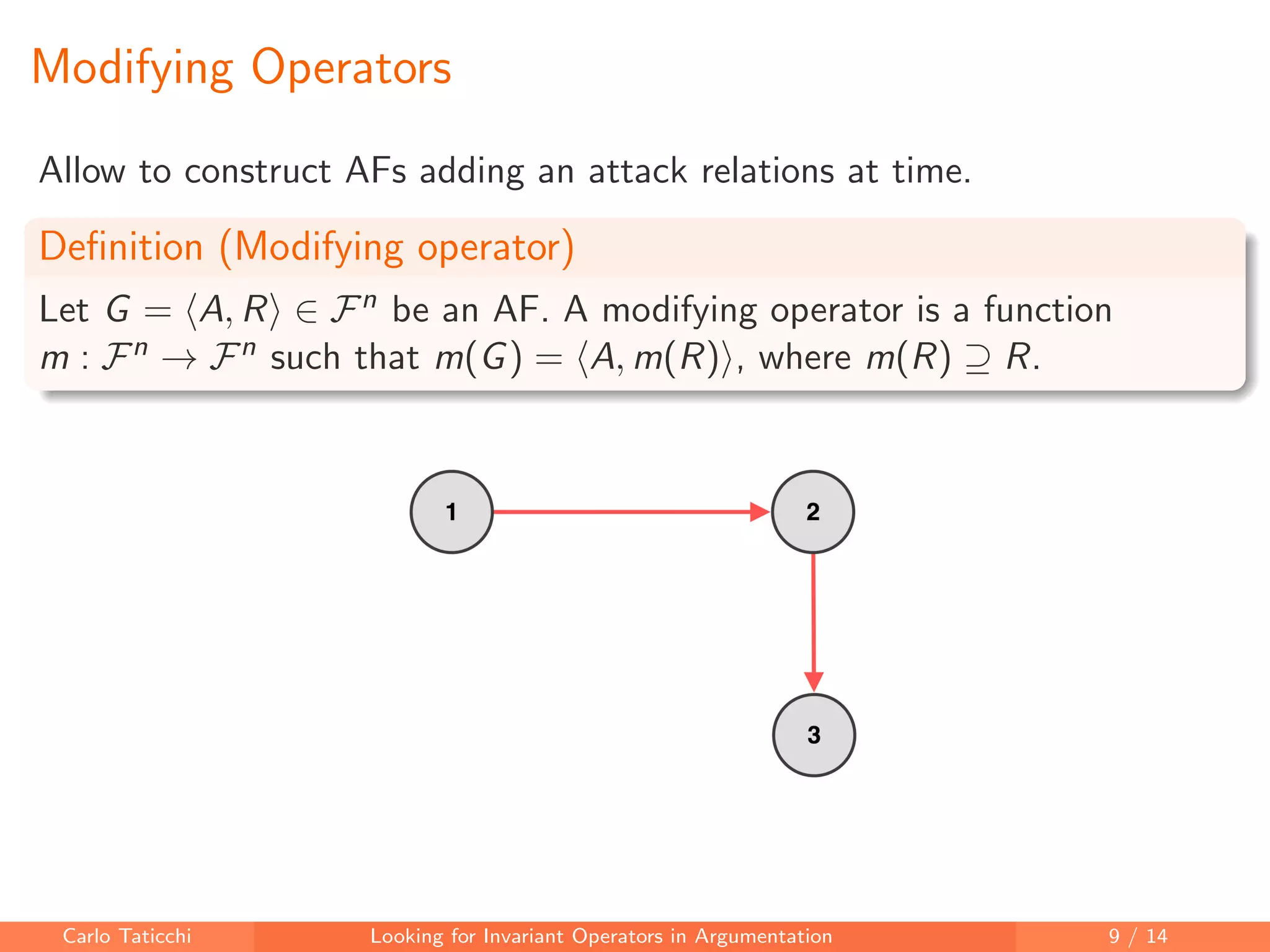
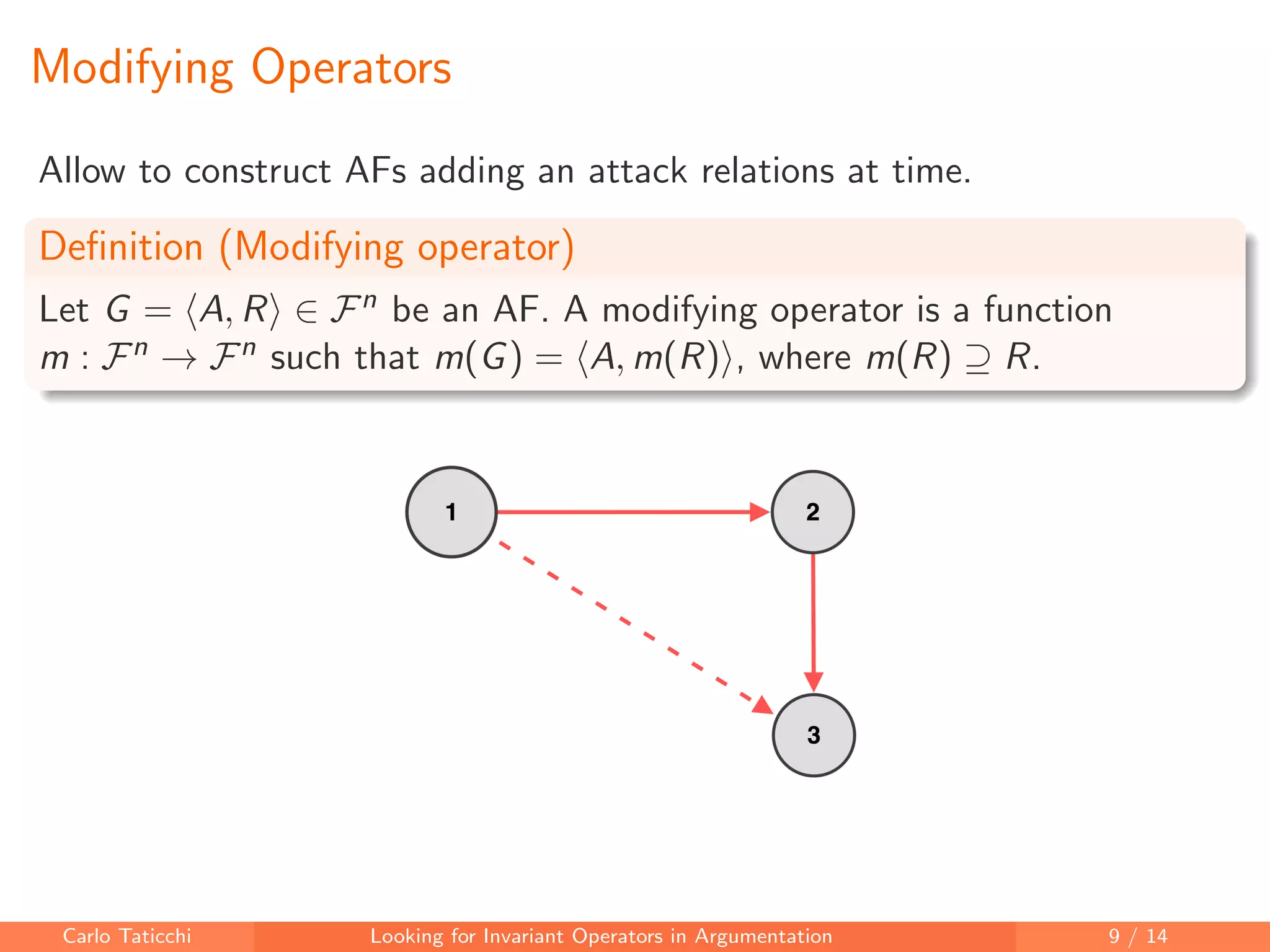
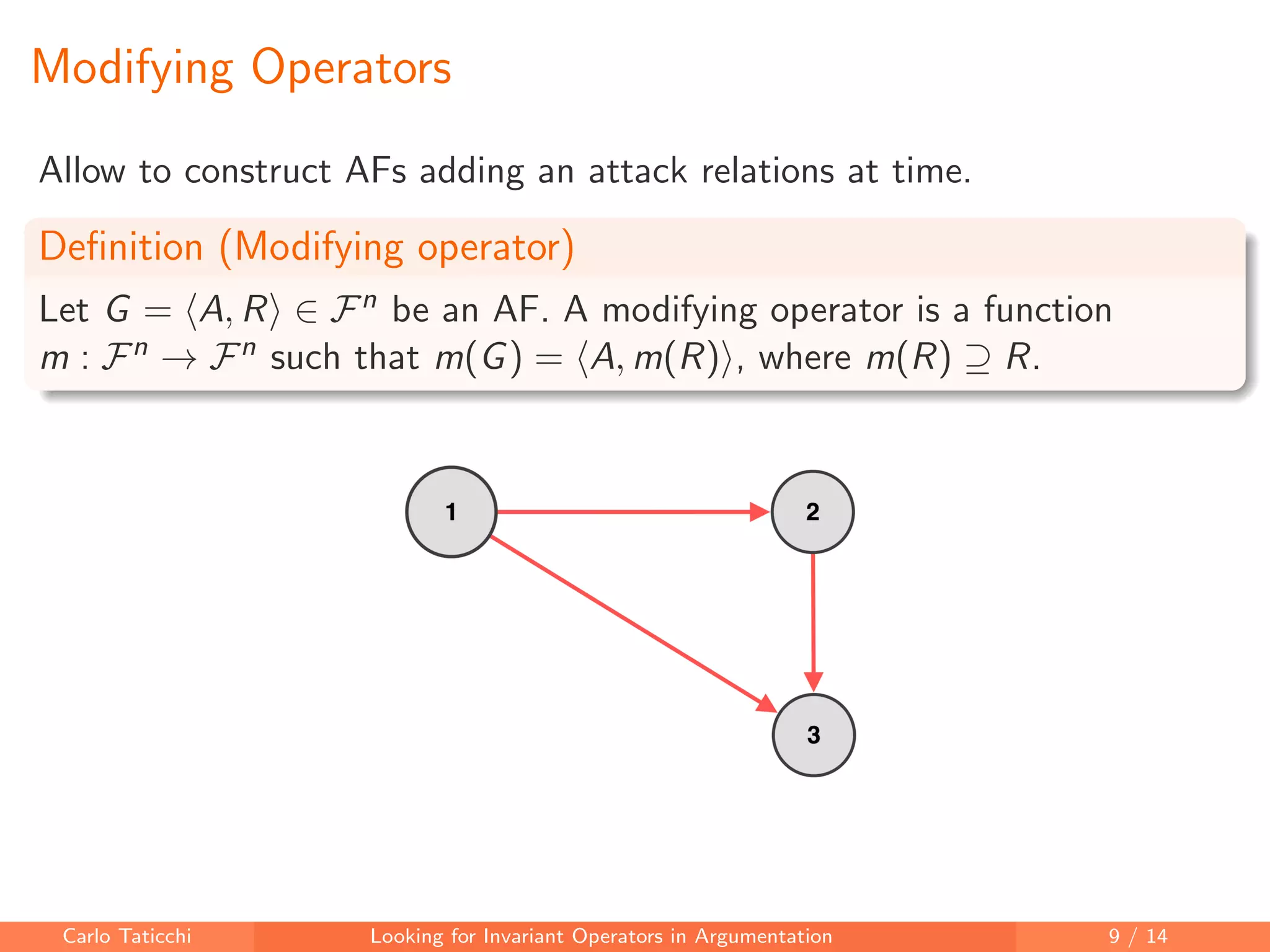
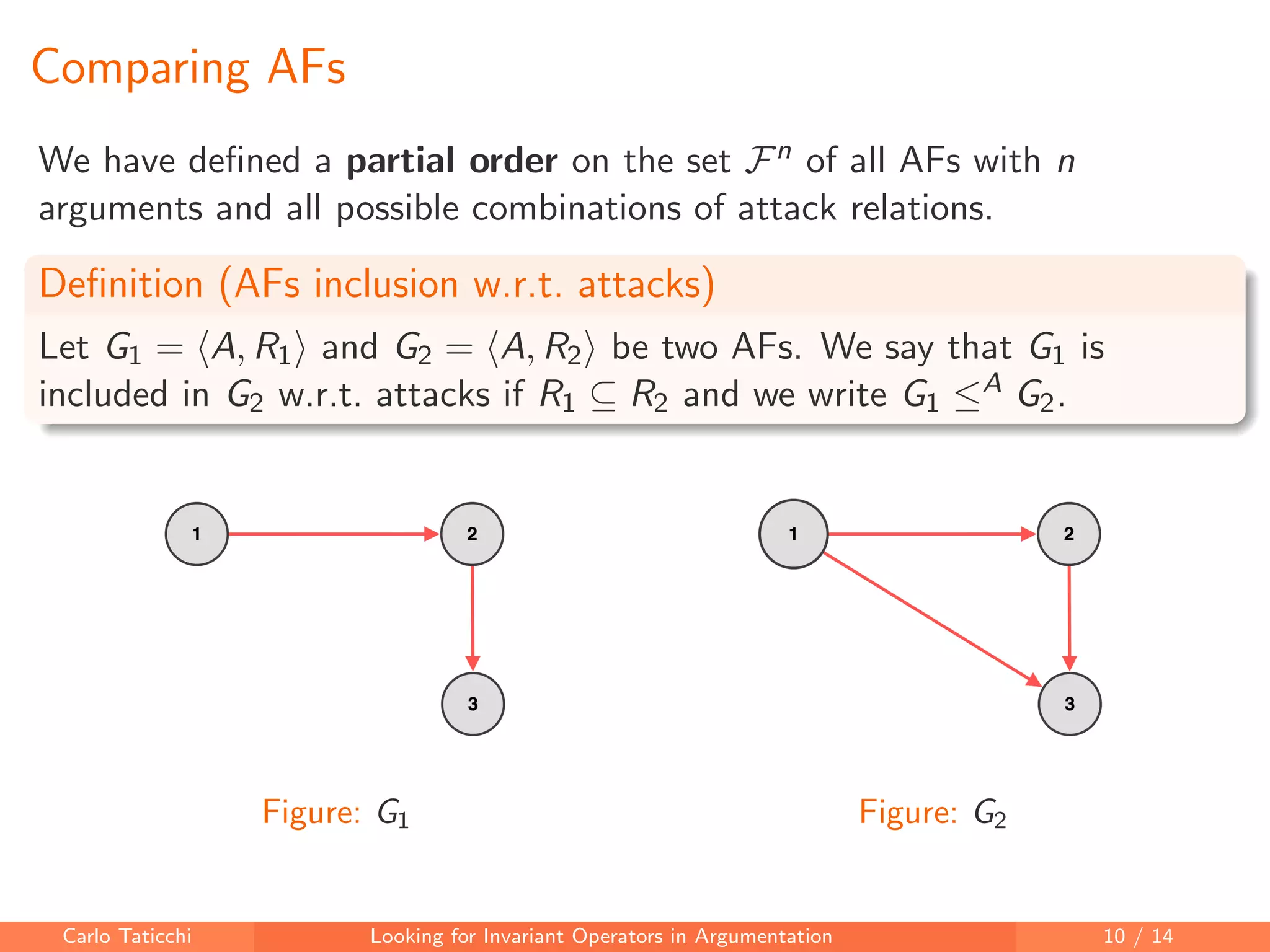
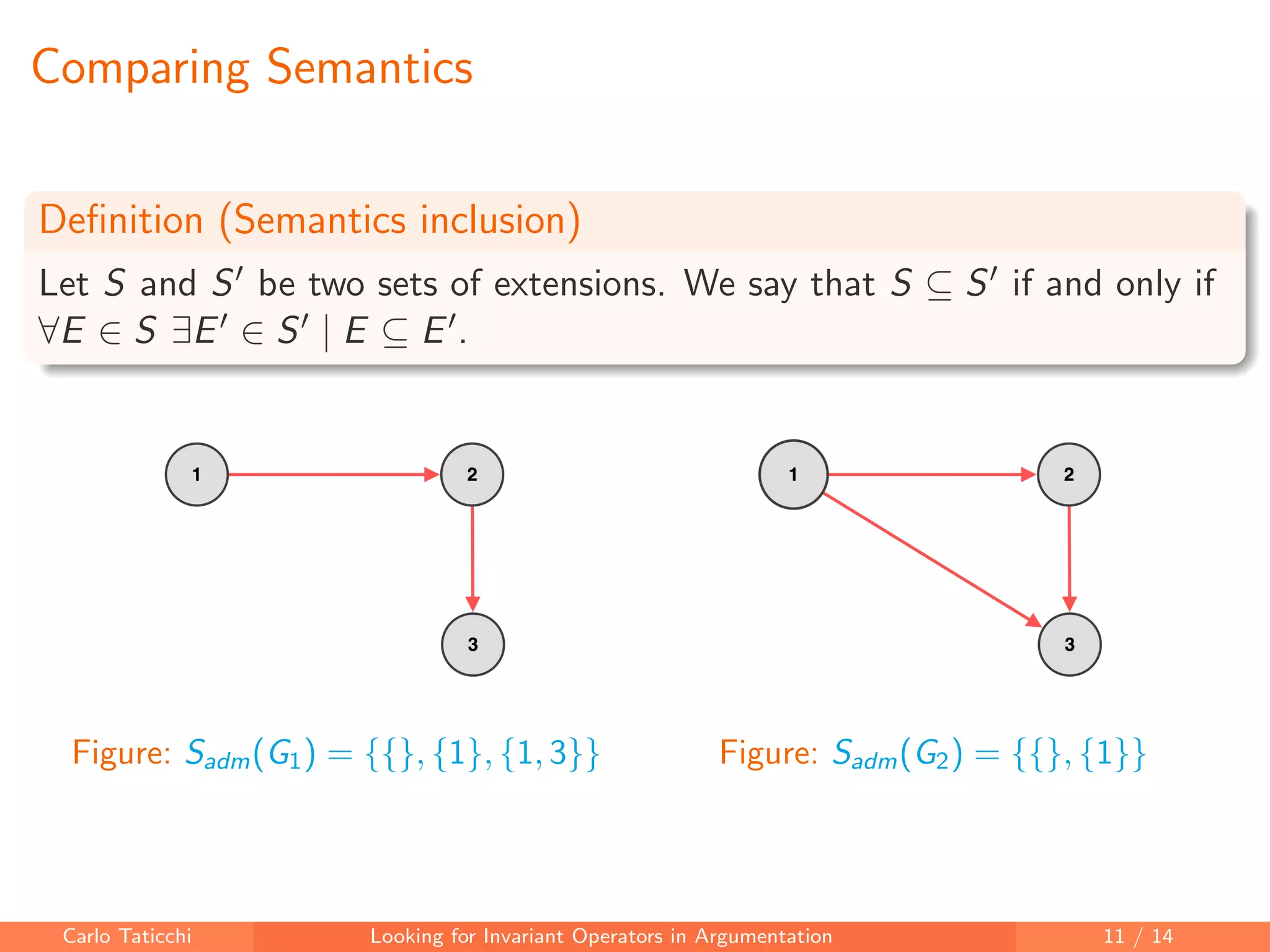
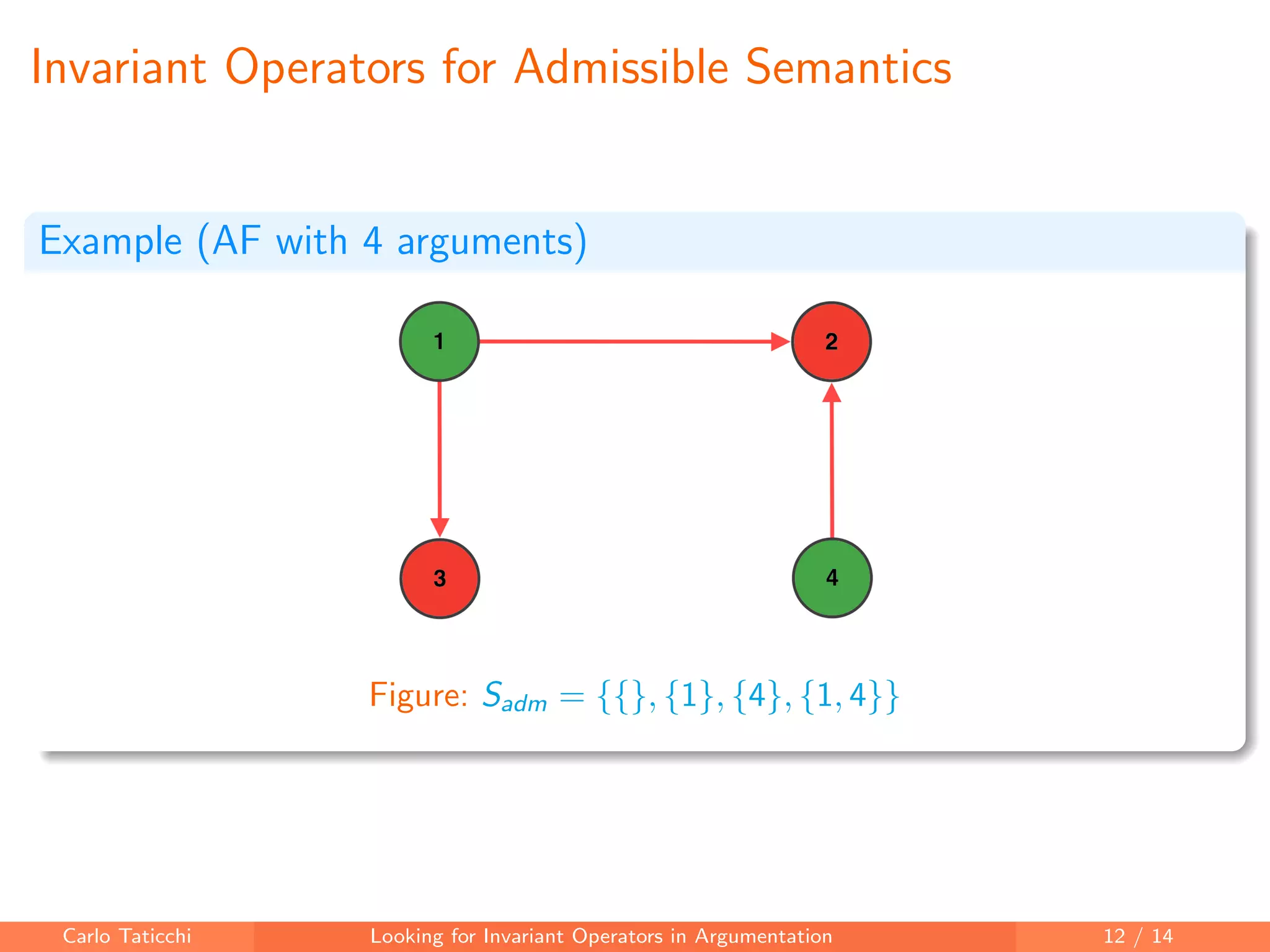
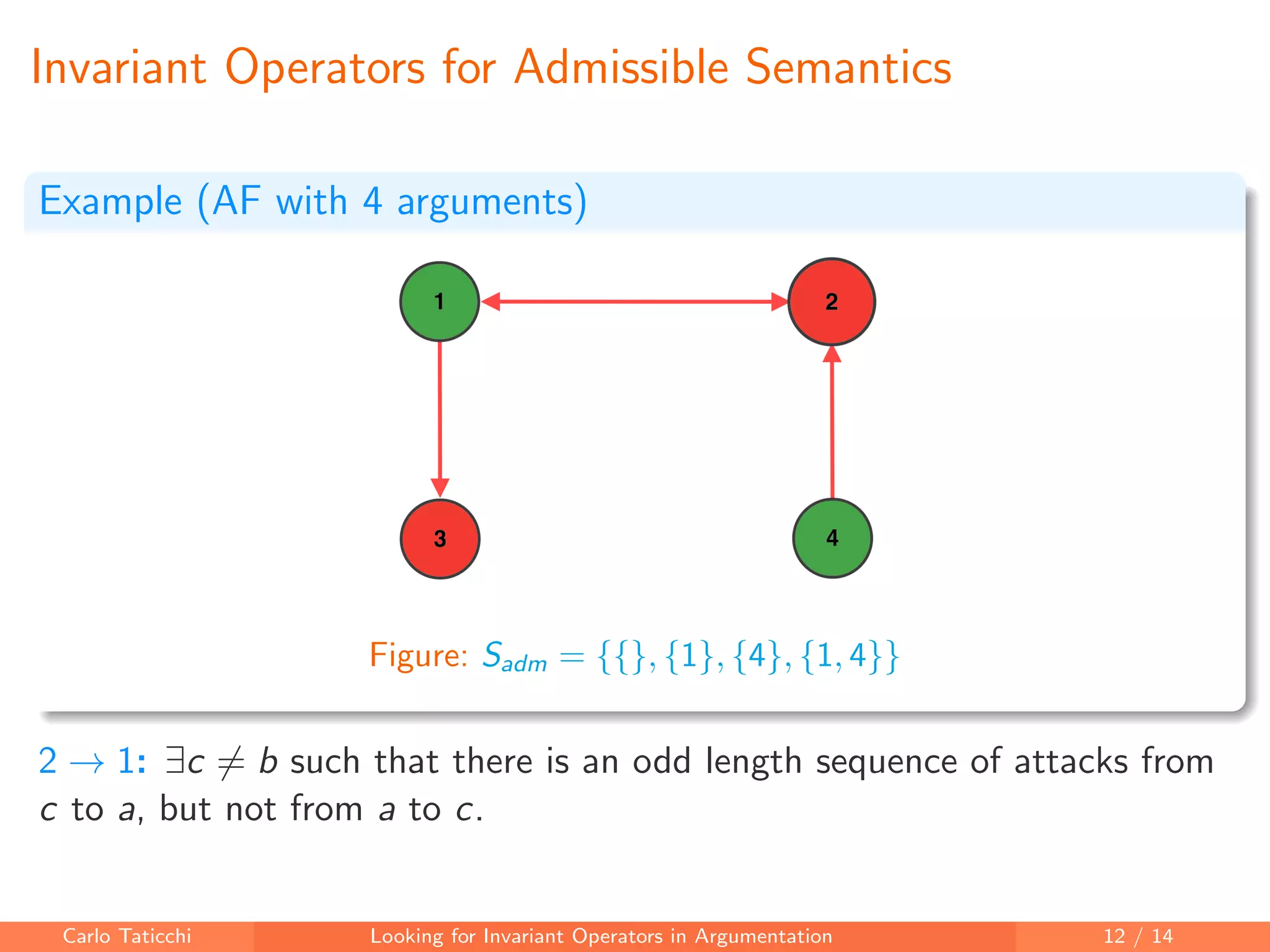
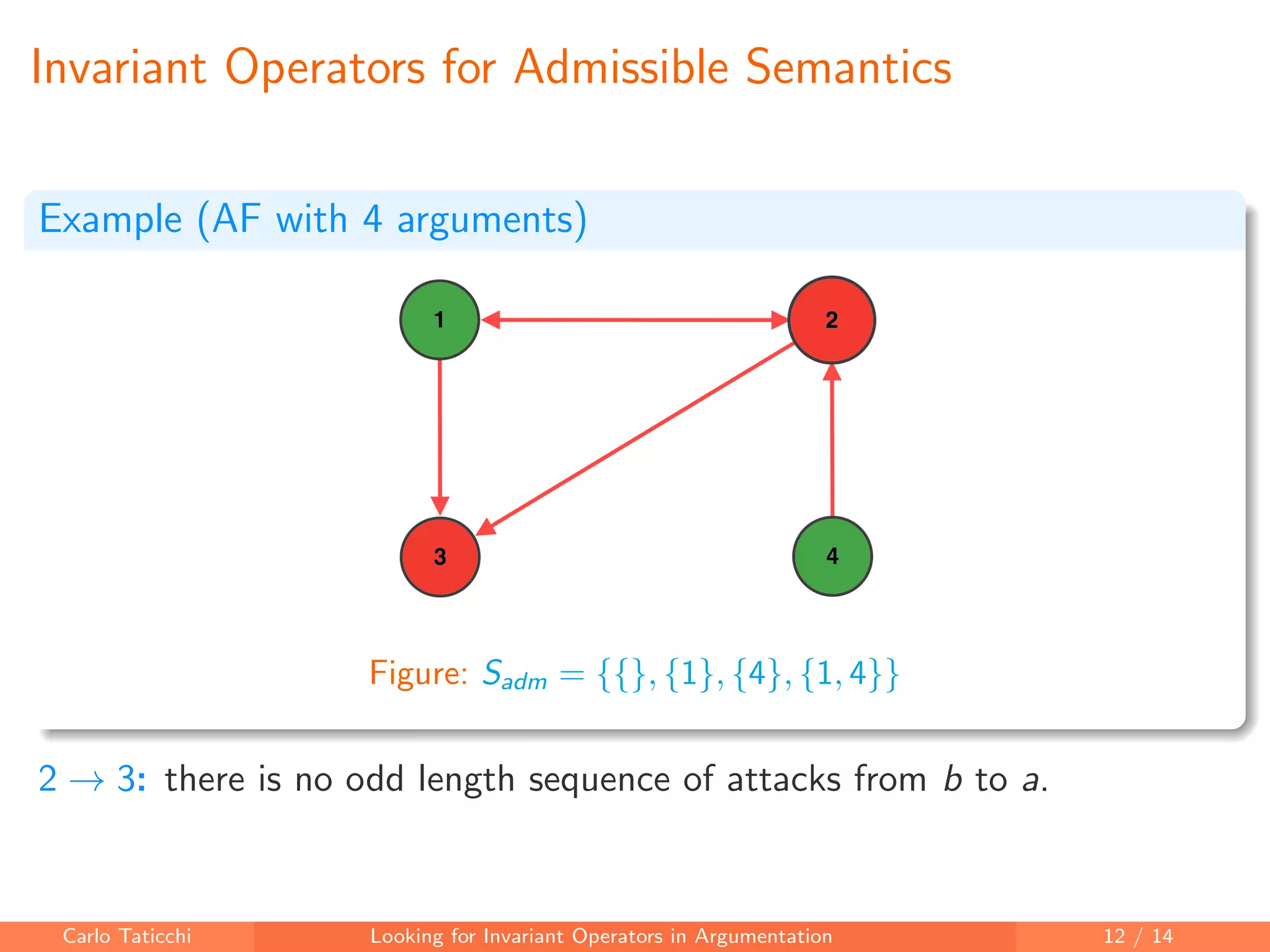
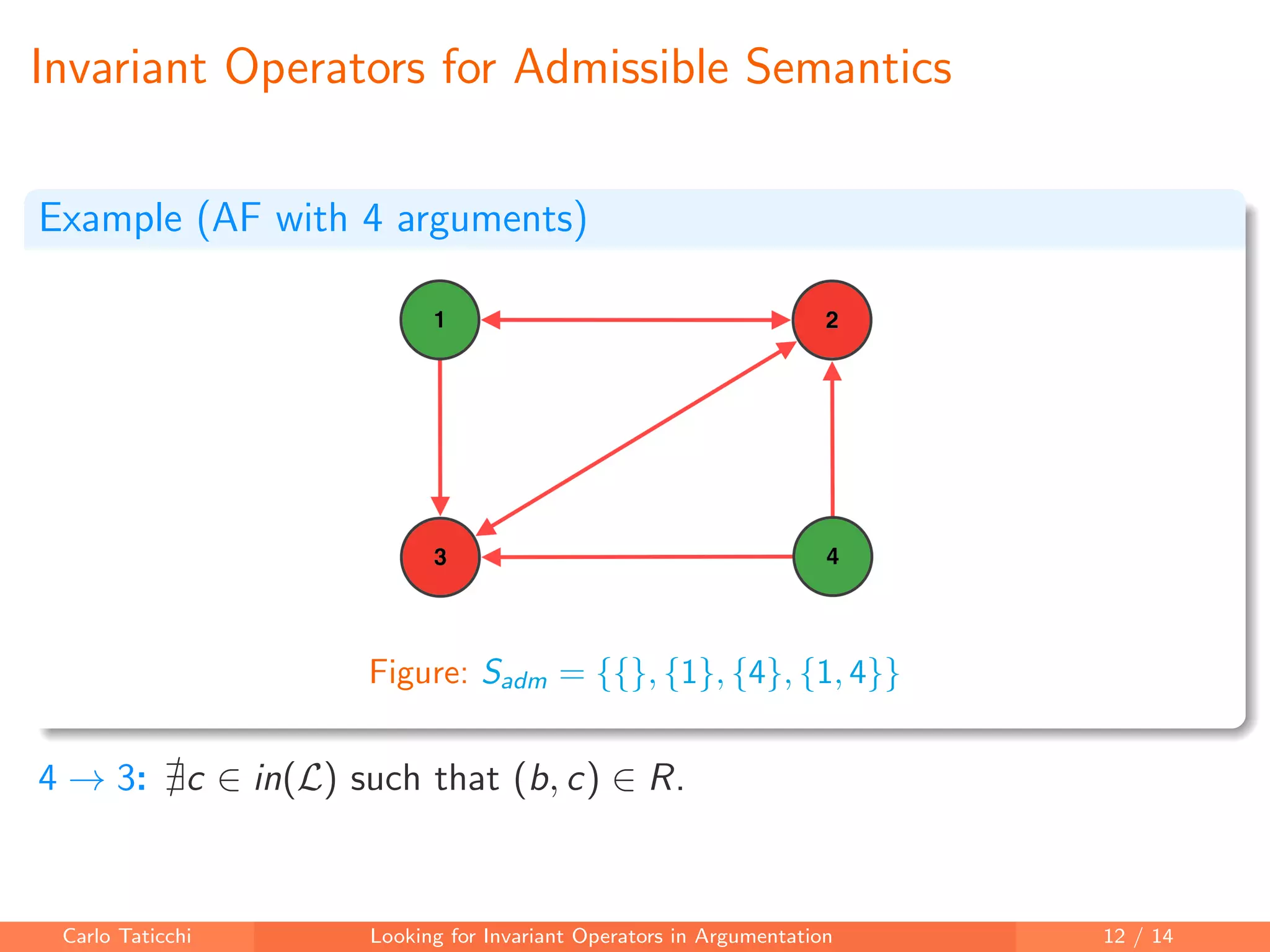
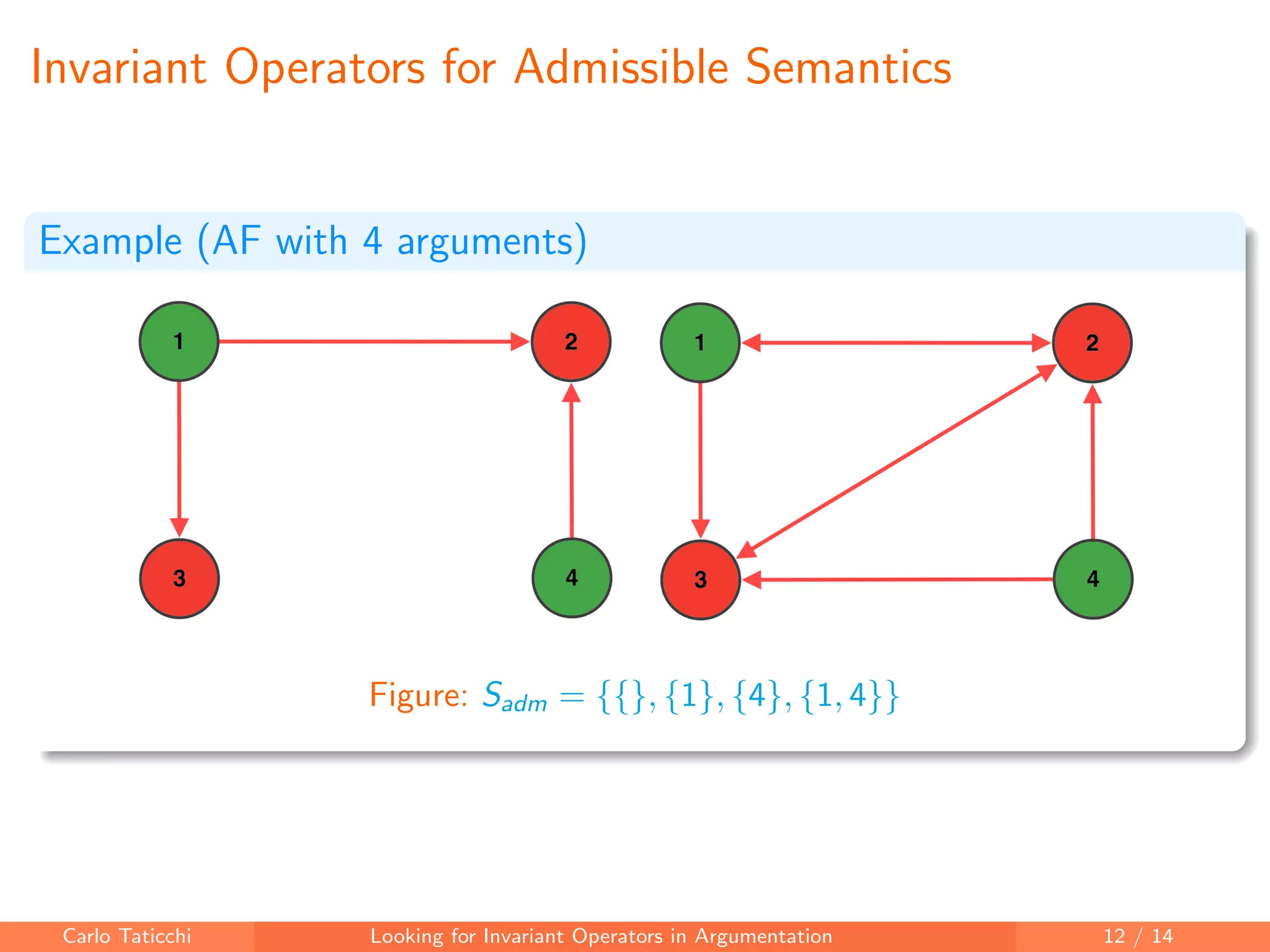
The document discusses looking for invariant operators in argumentation frameworks. It defines invariant operators as functions that modify argumentation frameworks by adding attack relations while maintaining the admissible semantics. The paper presents examples of invariant operators for admissible semantics and discusses directions for future work, including designing invariant operators for other semantics and considering additional modifications to argumentation frameworks.

1. Looking for Invariant Operators in Argumentation
Stefano Bistarelli1 Francesco Santini1 Carlo Taticchi2
stefano.bistarelli@unipg.it francesco.santini@unipg.it carlo.taticchi@gssi.it
1Universit`a degli Studi di Perugia, Italy
2Gran Sasso Science Institute (GSSI), L’Aquila, Italy

6. Index
1 Background - Argumentation Frameworks
2 Definition - Invariant Operators
3 Conclusion and Future Work
Carlo Taticchi Looking for Invariant Operators in Argumentation 3 / 14

7. Argumentation Frameworks1
A human-like fashion to deal with knowledge
Definition (AF)
An Abstract Argumentation Framework is a pair G = A, R where A is a
set of arguments and R is a binary relation on A.
1
PHAN MINH DUNG. On the Acceptability of Arguments and its Fundamental Role in Nonmonotonic Reasoning, Logic
Programming and n-Person Games. Artif. Intell., 77(2):321–358, 1995.
Carlo Taticchi Looking for Invariant Operators in Argumentation 4 / 14

8. Sets of Extensions
Definition (Conflict-free extensions)
Let G = A, R be an AF. A set E ⊆ A is conflict-free in G if there are no
a, b ∈ A | (a, b) ∈ R.
Carlo Taticchi Looking for Invariant Operators in Argumentation 5 / 14

9. Sets of Extensions
Definition (Conflict-free extensions)
Let G = A, R be an AF. A set E ⊆ A is conflict-free in G if there are no
a, b ∈ A | (a, b) ∈ R.
Scf (G) = {{}, {1}, {2}, {3}, {4}, {5},
{1, 2}, {1,4}, {1, 5}, {2,5}, {3, 5}, {1, 2, 5}}
Carlo Taticchi Looking for Invariant Operators in Argumentation 5 / 14

10. Dung’s Semantics
Definition (Admissible Semantics)
Let G = A, R be an AF. A set E ⊆ A is admissible in G if E is
conflict-free and each a ∈ E is defended by E.
Sadm(G) = {{}, {1},{2}, {3}, {4}, {5},
{1, 2},{1,4},{1, 5}, {2, 5}, {3, 5}, {1, 2, 5}}
Carlo Taticchi Looking for Invariant Operators in Argumentation 6 / 14

11. Dung’s Semantics
Definition (Admissible Semantics)
Let G = A, R be an AF. A set E ⊆ A is admissible in G if E is
conflict-free and each a ∈ E is defended by E.
Similar definitions for complete, grounded, preferred and stable.
Carlo Taticchi Looking for Invariant Operators in Argumentation 6 / 14

12. Reinstatement Labelling2
Every argument can be labelled in, out or undec.
Example (Labelling of an AF)
2
MARTIN CAMINADA. On the Issue of Reinstatement in Argumentation. Logics in Artificial Intelligence: 10th European
Conference, JELIA 2006 Liverpool, UK, September 13-15, 2006 Proceedings, pages 111–123, 2006.
Carlo Taticchi Looking for Invariant Operators in Argumentation 7 / 14

13. Robustness3,4
A property of an AF to withstand changes
Tries to answer the following questions:
• Is it possible to change the outcome of a debate according to a
particular semantics or meaning?
• If so, how easy could it be to perform such change?
• And which consequences does it bring?
3
S. BISTARELLI, F. FALOCI, F. SANTINI, AND C. TATICCHI. Robustness in abstract argumentation frameworks. In
Proceedings of the 29th International Florida Artificial Intelligence Research Society Conf. FLAIRS, page 703, 2016.
4
CARLO TATICCHI. A Study of Robustness in Abstract Argumentation Frameworks. Proceedings of the Doctoral
Consortium of AI*IA 2016, Genova, Italy, November 29, 2016, pages 11–16. CEUR-WS.org, 2016.
Carlo Taticchi Looking for Invariant Operators in Argumentation 8 / 14

14. Modifying Operators
Allow to construct AFs adding an attack relations at time.
Definition (Modifying operator)
Let G = A, R ∈ Fn be an AF. A modifying operator is a function
m : Fn → Fn such that m(G) = A, m(R) , where m(R) ⊇ R.
Carlo Taticchi Looking for Invariant Operators in Argumentation 9 / 14

15. Modifying Operators
Allow to construct AFs adding an attack relations at time.
Definition (Modifying operator)
Let G = A, R ∈ Fn be an AF. A modifying operator is a function
m : Fn → Fn such that m(G) = A, m(R) , where m(R) ⊇ R.
Carlo Taticchi Looking for Invariant Operators in Argumentation 9 / 14

16. Modifying Operators
Allow to construct AFs adding an attack relations at time.
Definition (Modifying operator)
Let G = A, R ∈ Fn be an AF. A modifying operator is a function
m : Fn → Fn such that m(G) = A, m(R) , where m(R) ⊇ R.
Carlo Taticchi Looking for Invariant Operators in Argumentation 9 / 14

17. Comparing AFs
We have defined a partial order on the set Fn of all AFs with n
arguments and all possible combinations of attack relations.
Definition (AFs inclusion w.r.t. attacks)
Let G1 = A, R1 and G2 = A, R2 be two AFs. We say that G1 is
included in G2 w.r.t. attacks if R1 ⊆ R2 and we write G1 ≤A G2.
Figure: G1 Figure: G2
Carlo Taticchi Looking for Invariant Operators in Argumentation 10 / 14

18. Comparing Semantics
Definition (Semantics inclusion)
Let S and S be two sets of extensions. We say that S ⊆ S if and only if
∀E ∈ S ∃E ∈ S | E ⊆ E .
Figure: Sadm(G1) = {{}, {1}, {1, 3}} Figure: Sadm(G2) = {{}, {1}}
Carlo Taticchi Looking for Invariant Operators in Argumentation 11 / 14

19. Invariant Operators for Admissible Semantics
Example (AF with 4 arguments)
Figure: Sadm = {{}, {1}, {4}, {1, 4}}
Carlo Taticchi Looking for Invariant Operators in Argumentation 12 / 14

20. Invariant Operators for Admissible Semantics
Example (AF with 4 arguments)
Figure: Sadm = {{}, {1}, {4}, {1, 4}}
2 → 1: ∃c = b such that there is an odd length sequence of attacks from
c to a, but not from a to c.
Carlo Taticchi Looking for Invariant Operators in Argumentation 12 / 14

21. Invariant Operators for Admissible Semantics
Example (AF with 4 arguments)
Figure: Sadm = {{}, {1}, {4}, {1, 4}}
2 → 3: there is no odd length sequence of attacks from b to a.
Carlo Taticchi Looking for Invariant Operators in Argumentation 12 / 14

22. Invariant Operators for Admissible Semantics
Example (AF with 4 arguments)
Figure: Sadm = {{}, {1}, {4}, {1, 4}}
4 → 3: c ∈ in(L) such that (b, c) ∈ R.
Carlo Taticchi Looking for Invariant Operators in Argumentation 12 / 14

23. Invariant Operators for Admissible Semantics
Example (AF with 4 arguments)
Figure: Sadm = {{}, {1}, {4}, {1, 4}}
Carlo Taticchi Looking for Invariant Operators in Argumentation 12 / 14

24. Summing Up
Invariant local expansion operators for the admissible semantics allow for:
• adding an attack in an AF, while
• maintaining the admissible semantics unchanged
a → b Condition
in → in never possible
in → out c ∈ in(L) | (b, c) ∈ R
in → undec c ∈ undec(L) | (c, c) /∈ R and (b, c) ∈ R
out → in (b, a) ∈ R or ∃c ∈ out | (c, b) ∈ R
out →
in there is no odd length sequence of attacks from b to a
out → out or ∃c = b | there is an odd length sequence of attacks
undec from c to a, but not from a to c
undec → in never possible
undec → out no condition required
undec → undec no condition required
Carlo Taticchi Looking for Invariant Operators in Argumentation 13 / 14

25. Further Research
Next possible steps:
• To design invariant operators with respect to the complete,
grounded, preferred, semi-stable, and stable semantics.
• To find the essential extensions for which every change inside
modifies the semantics, while changes outside do not.
• To study local expansion operators also for semiring-based
weighted AFs5.
• To consider different notions of equivalence6 (e.g. local
equivalence) and additional modifications of AFs (as the deletion of
attack or the addition/removal of arguments).
5
S. BISTARELLI, F. ROSSI, AND F. SANTINI. A Collective Defence Against Grouped Attacks for Weighted Abstract
Argumentation Frameworks. FLAIRS Conference 2016: 638-643
6
E. OIKARINEN, AND S. WOLTRAN. Characterizing strong equivalence for argumentation frameworks. 2011. Artificial
Intelligence 175(14-15):1985–2009.
Carlo Taticchi Looking for Invariant Operators in Argumentation 14 / 14

26. Further Research
Next possible steps:
• To design invariant operators with respect to the complete,
grounded, preferred, semi-stable, and stable semantics.
• To find the essential extensions for which every change inside
modifies the semantics, while changes outside do not.
• To study local expansion operators also for semiring-based
weighted AFs5.
• To consider different notions of equivalence6 (e.g. local
equivalence) and additional modifications of AFs (as the deletion of
attack or the addition/removal of arguments).
5
S. BISTARELLI, F. ROSSI, AND F. SANTINI. A Collective Defence Against Grouped Attacks for Weighted Abstract
Argumentation Frameworks. FLAIRS Conference 2016: 638-643
6
E. OIKARINEN, AND S. WOLTRAN. Characterizing strong equivalence for argumentation frameworks. 2011. Artificial
Intelligence 175(14-15):1985–2009.
Carlo Taticchi Looking for Invariant Operators in Argumentation 14 / 14

27. Further Research
Next possible steps:
• To design invariant operators with respect to the complete,
grounded, preferred, semi-stable, and stable semantics.
• To find the essential extensions for which every change inside
modifies the semantics, while changes outside do not.
• To study local expansion operators also for semiring-based
weighted AFs5.
• To consider different notions of equivalence6 (e.g. local
equivalence) and additional modifications of AFs (as the deletion of
attack or the addition/removal of arguments).
5
S. BISTARELLI, F. ROSSI, AND F. SANTINI. A Collective Defence Against Grouped Attacks for Weighted Abstract
Argumentation Frameworks. FLAIRS Conference 2016: 638-643
6
E. OIKARINEN, AND S. WOLTRAN. Characterizing strong equivalence for argumentation frameworks. 2011. Artificial
Intelligence 175(14-15):1985–2009.
Carlo Taticchi Looking for Invariant Operators in Argumentation 14 / 14

28. Further Research
Next possible steps:
• To design invariant operators with respect to the complete,
grounded, preferred, semi-stable, and stable semantics.
• To find the essential extensions for which every change inside
modifies the semantics, while changes outside do not.
• To study local expansion operators also for semiring-based
weighted AFs5.
• To consider different notions of equivalence6 (e.g. local
equivalence) and additional modifications of AFs (as the deletion of
attack or the addition/removal of arguments).
5
S. BISTARELLI, F. ROSSI, AND F. SANTINI. A Collective Defence Against Grouped Attacks for Weighted Abstract
Argumentation Frameworks. FLAIRS Conference 2016: 638-643
6
E. OIKARINEN, AND S. WOLTRAN. Characterizing strong equivalence for argumentation frameworks. 2011. Artificial
Intelligence 175(14-15):1985–2009.
Carlo Taticchi Looking for Invariant Operators in Argumentation 14 / 14

29. Looking for Invariant Operators in Argumentation
Stefano Bistarelli1 Francesco Santini1 Carlo Taticchi2
stefano.bistarelli@unipg.it francesco.santini@unipg.it carlo.taticchi@gssi.it
Thanks for your attention!
Questions?
1Universit`a degli Studi di Perugia, Italy
2Gran Sasso Science Institute (GSSI), L’Aquila, Italy