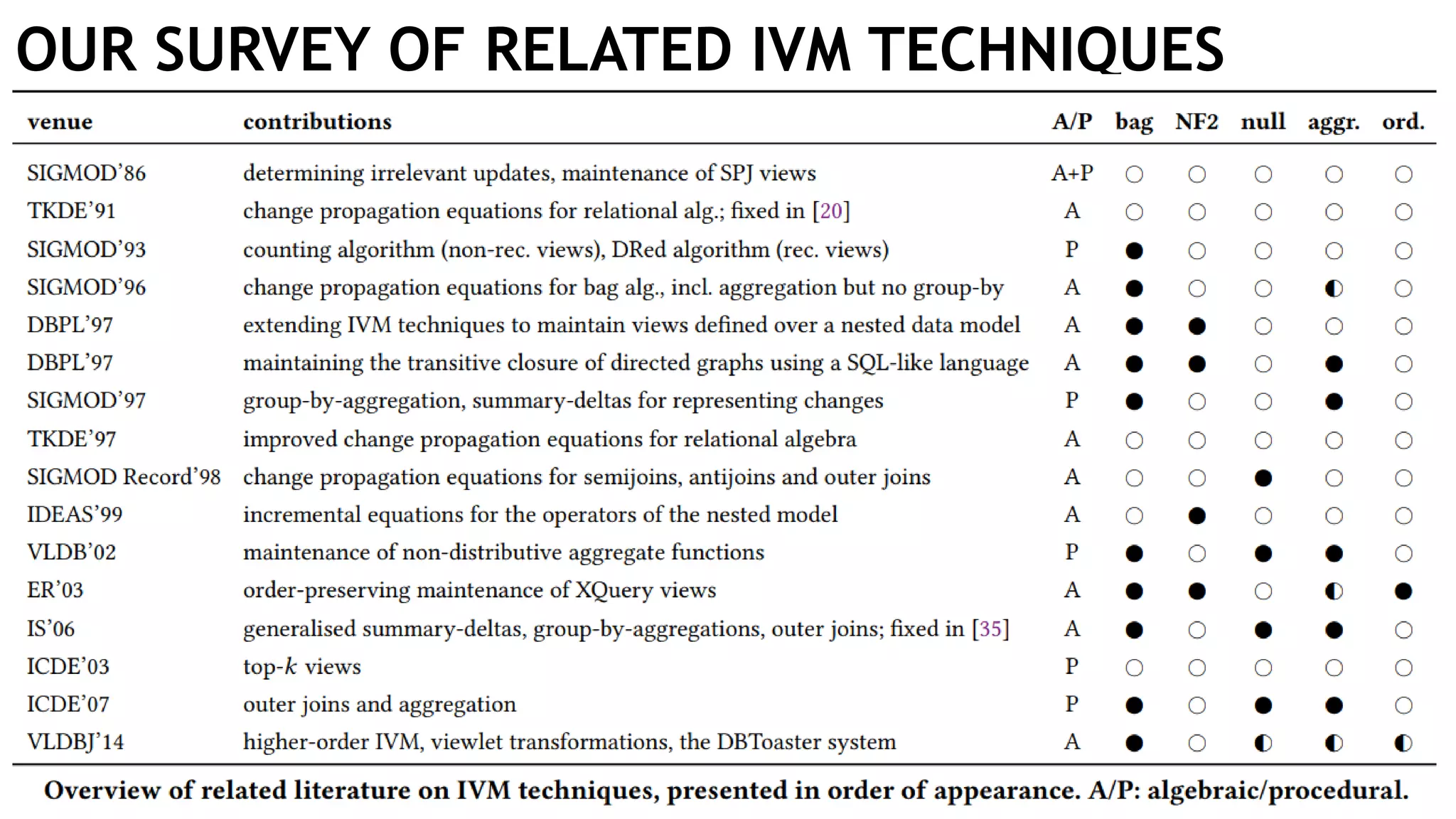
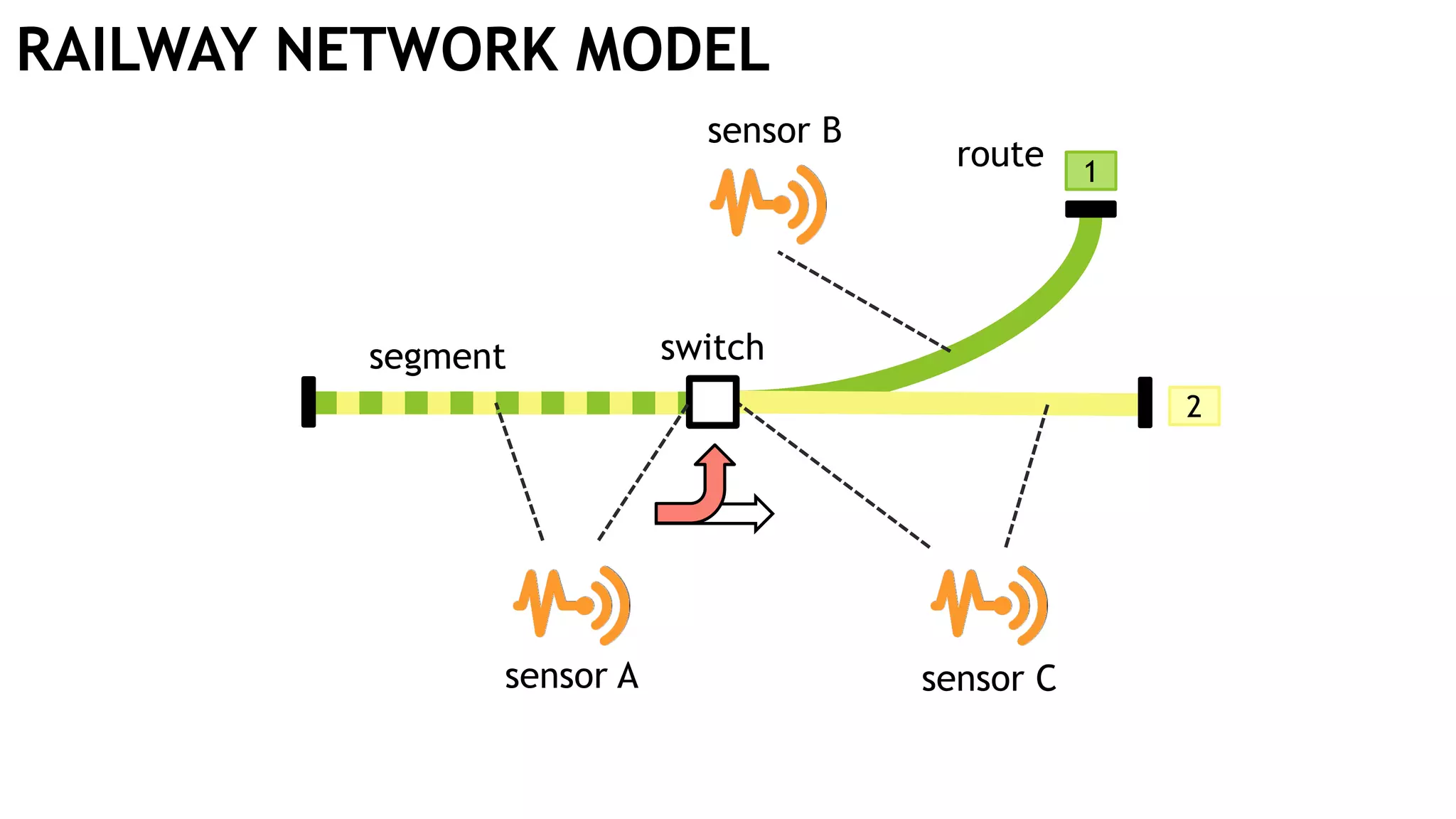
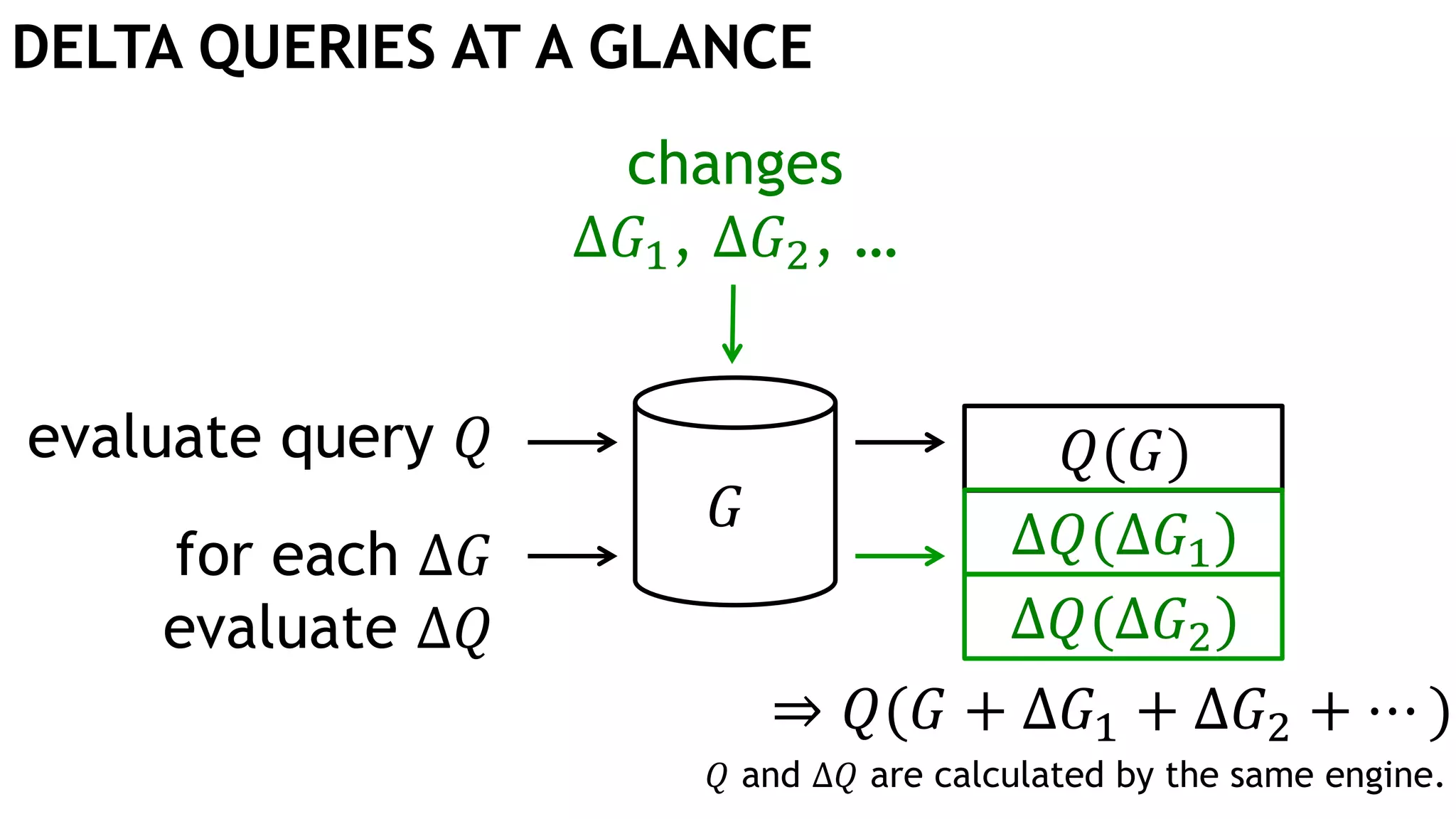
The document discusses incremental view maintenance (IVM) for OpenCypher queries, focusing on graph applications like model validation and recommendation systems. It presents approaches to map IVM to relational algebra and provides examples of delta queries for graph modifications. The paper notes the complexities of integrating IVM techniques with the property graph data model and Cypher language.


![MODEL VALIDATION
Implemented with model queries
Models are typed, attributed graphs
Typical queries
o Get two components connected by a particular edge
MATCH (r:R)…(s:S) WHERE NOT (r)-[:E]->(s)
o Check if two objects are reachable
MATCH (r:R)…(s:S) WHERE NOT (r)-[:E1|E2*]->(s)
o Property checks
MATCH (r:R)-->(s:S) WHERE r.a = 'x' OR (s:Y)
Complex graph queries](https://image.slidesharecdn.com/ocim4-ivm-180525103338/75/Incremental-View-Maintenance-for-openCypher-Queries-3-2048.jpg)
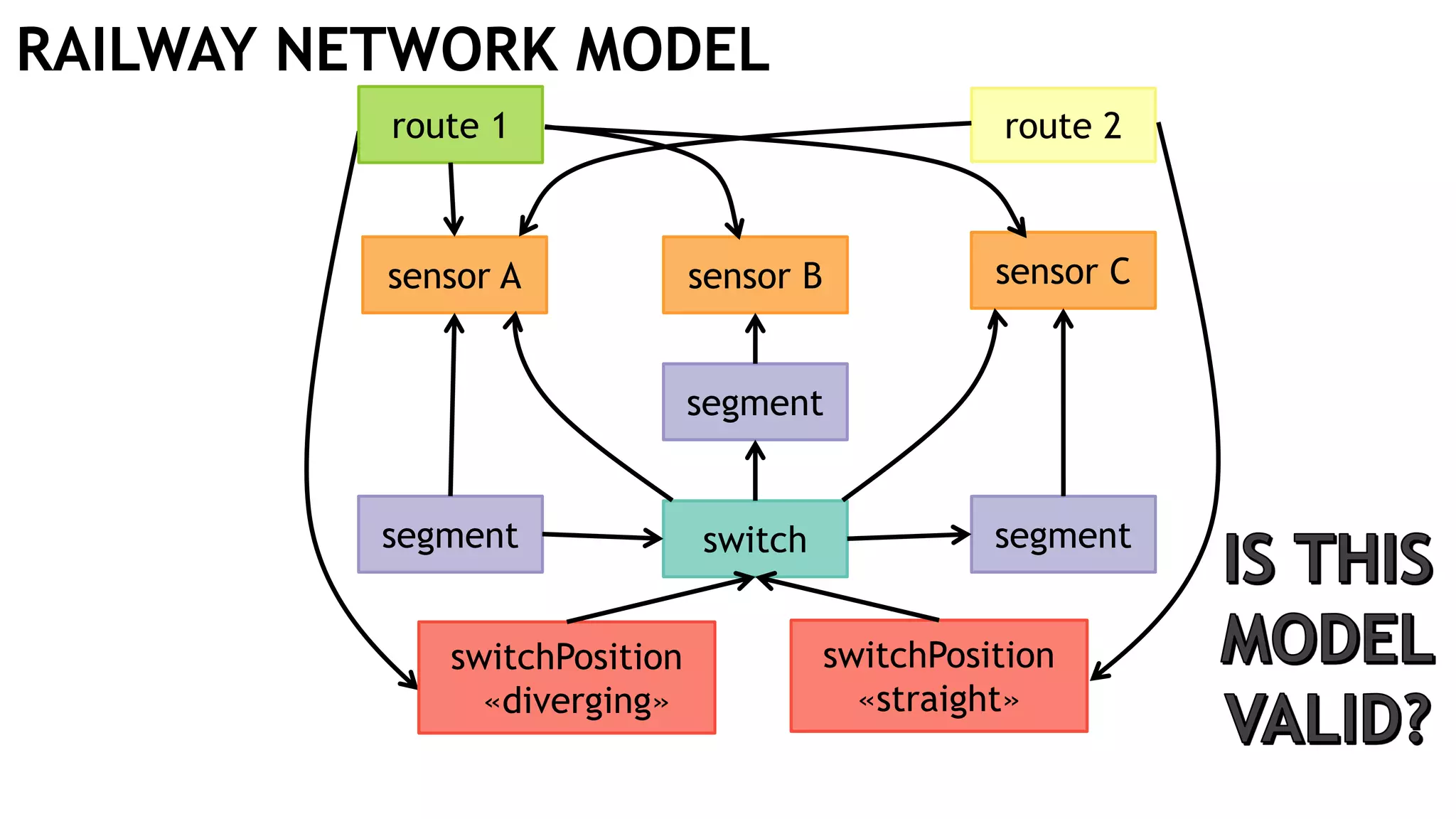
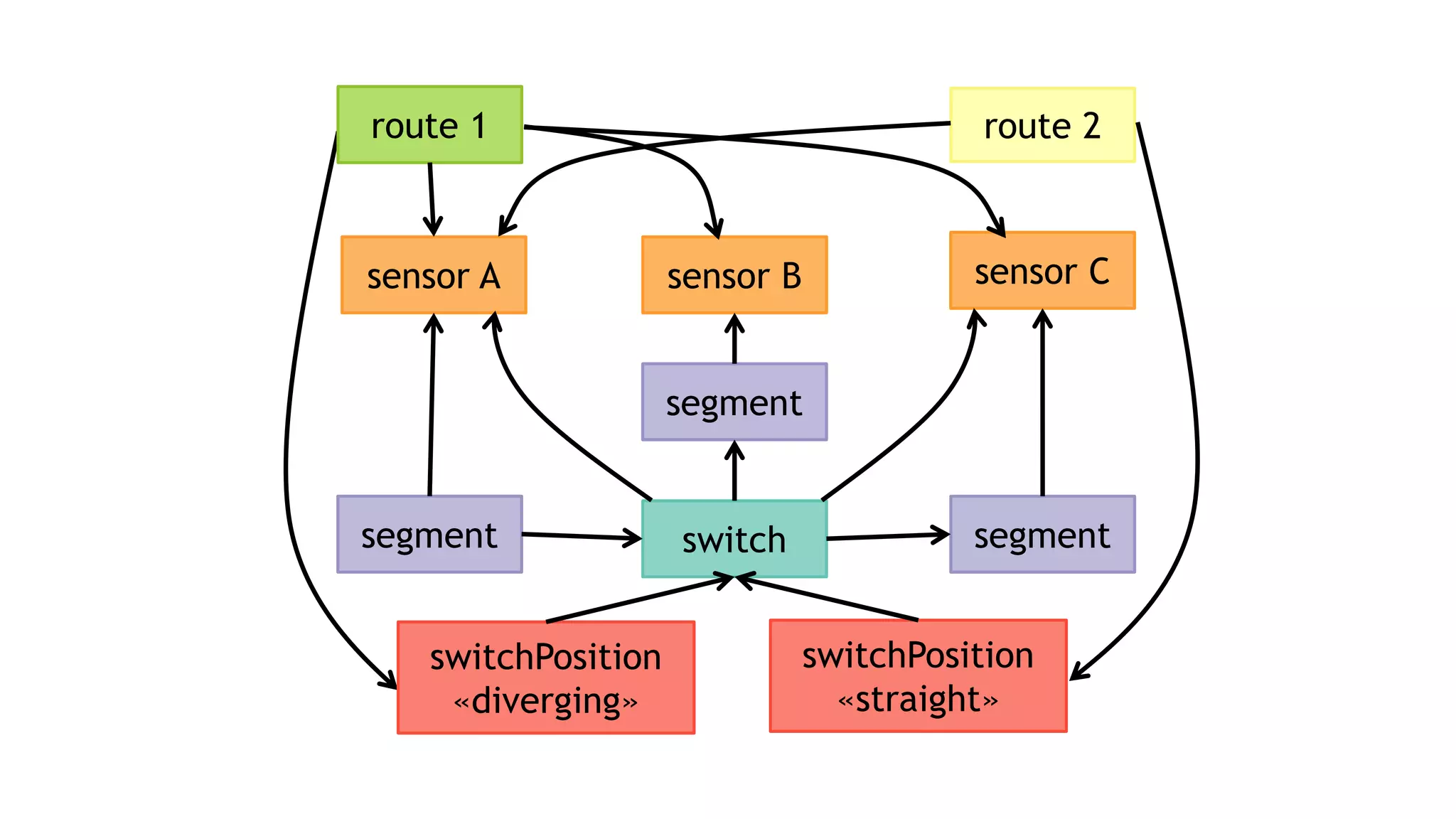
![:FOLLOWS
:MONITORED_BY
:TARGET:REQUIRES
MATCH (route:Route)
-[:FOLLOWS]->(swP:SwitchPosition)
-[:TARGET]->(sw:Switch)
-[:MONITORED_BY]->(sensor:Sensor)
WHERE NOT (route)-[:REQUIRES]->(sensor)
RETURN route, sensor, swP, sw
sw: Switchsensor: Sensor
route: Route swP: SwitchPosition
G. Szárnyas, B. Izsó, I. Ráth, D. Varró:
The Train Benchmark: cross-technology performance
evaluation of continuous model queries.
Software and Systems Modeling, 2017](https://image.slidesharecdn.com/ocim4-ivm-180525103338/75/Incremental-View-Maintenance-for-openCypher-Queries-7-2048.jpg)







![v1 v2 v3
1 2 3
1 2 6
RELATIONAL ALGEBRA FOR CYPHER
Natural join: 𝑟 ⋈ 𝑠
MATCH (v1)-[:r]->(v2)-[:s]->(v3)
RETURN *
Semijoin: 𝑟 ⋉ 𝑠
MATCH (v1)-[:r]->(v2)
WHERE (v2)-[:s]->()
Antijoin: 𝑟 ഥ⋉ 𝑠
MATCH (v1)-[:r]->(v2)
WHERE NOT (v2)-[:s]->()
Left outer join: 𝑟 ⟕ 𝑠
MATCH (v1)-[:r]->(v2)
OPTIONAL MATCH (v2)-[:s]->(v3)
1 3
4
2
5 6
:r
:r
:s
:s
v1 v2
1 2
v1 v2
4 5
1 3
4
2
5 6
:r
:r
:s
:s
1 3
4
2
5 6
:r
:r
:s
:s
1 3
4
2
5 6
:r
:r
:s
:s
1 32
6
:r :s
:s
1 2:r
4 5
:r
1 3
4
2
5 6
:r
:r
:s
:s
v1 v2 v3
1 2 3
1 2 6
4 5 null
4 5
v1 v2 v3
1 2 3
1 2 6](https://image.slidesharecdn.com/ocim4-ivm-180525103338/75/Incremental-View-Maintenance-for-openCypher-Queries-26-2048.jpg)



![EXAMPLE QUERY #1
MATCH (v1)-[:a]->(v2)-[:b]->(v3)-[:c]->(v4)
RETURN v1, v2, v3, v4
Relational algebra expression: 𝑎 ⋈ 𝑏 ⋈ 𝑐
Δ 𝑎 ⋈ 𝑏 ⋈ 𝑐
= 𝑎 ⋈ 𝑏 𝑚
⋈ Δ𝑐 + Δ 𝑎 ⋈ 𝑏 ⋈ 𝑐 𝑚
= 𝑎 ⋈ 𝑏 𝑚
⋈ Δ𝑐 + 𝑎 𝑚
⋈ Δ𝑏 ⋈ 𝑐 𝑚
+ Δ𝑎 ⋈ 𝑏 𝑚
⋈ 𝑐 𝑚
= 𝑎 𝑚
⋈ 𝑏 𝑚
⋈ Δ𝑐 + 𝑎 𝑚
⋈ Δ𝑏 ⋈ 𝑐 𝑚
+ Δ𝑎 ⋈ 𝑏 𝑚
⋈ 𝑐 𝑚
Similarly to 𝛻 𝑎 ⋈ 𝑏 ⋈ 𝑐 .
v1 v2 v3
:b:a
𝑎 𝑣1, 𝑣2
𝑏 𝑣2, 𝑣3
𝑐 𝑣3, 𝑣4
v4
:c](https://image.slidesharecdn.com/ocim4-ivm-180525103338/75/Incremental-View-Maintenance-for-openCypher-Queries-30-2048.jpg)
![EXAMPLE QUERY #1
MATCH (v1)-[:a]->(v2)-[:b]->(v3)-[:c]->(v4)
RETURN v1, v2, v3, v4
Δ 𝑎 ⋈ 𝑏 ⋈ 𝑐
= 𝑎 𝑚
⋈ 𝑏 𝑚
⋈ Δ𝑐 + 𝑎 𝑚
⋈ Δ𝑏 ⋈ 𝑐 𝑚
+ Δ𝑎 ⋈ 𝑏 𝑚
⋈ 𝑐 𝑚
UNWIND $pcs AS pc
MATCH (v1)-[:a]->(v2)-[:b]->(v3)-[pc]->(v4)
RETURN v1, v2, v3, v4
$pcs -> pass lists of nodes/edges as parameters
// This only works in embedded mode, see neo4j/issues/10239
v1 v2 v3
:b:a
𝑎 𝑣1, 𝑣2
𝑏 𝑣2, 𝑣3
𝑐 𝑣3, 𝑣4
v4
:c](https://image.slidesharecdn.com/ocim4-ivm-180525103338/75/Incremental-View-Maintenance-for-openCypher-Queries-31-2048.jpg)
![POSITIVE DELTA QUERY FOR 𝑎 ⋈ 𝑏 ⋈ 𝑐
// r1 = a⋈b⋈Δc
UNWIND $pcs AS pc
MATCH (v1)-[:a]->(v2)-[:b]->(v3)-[pc]->(v4)
RETURN v1, v2, v3, v4
UNION ALL
// r2 = a⋈Δb⋈c
UNWIND $pbs AS pb
MATCH (v1)-[:a]->(v2)-[pb]->(v3)-[:c]->(v4)
RETURN v1, v2, v3, v4
UNION ALL
// r3 = Δa⋈b⋈c
UNWIND $pas AS pa
MATCH (v1)-[pa]->(v2)-[:b]->(v3)-[:c]->(v4)
RETURN v1, v2, v3, v4](https://image.slidesharecdn.com/ocim4-ivm-180525103338/75/Incremental-View-Maintenance-for-openCypher-Queries-32-2048.jpg)
![POSITIVE DELTA QUERY FOR 𝑎 ⋈ 𝑏 ⋈ 𝑐
Long WITH chains are cumbersome -> patterns+list comprehensions.
WITH [pc IN $pcs | // r1 = a⋈b⋈Δc
[(v1)-[:a]->(v2)-[:b]->(v3)-[pc]->(v4) |
[v1, v2, v3, v4]]]
[pb IN $pbs | // r2 = a⋈Δb⋈c
[(v1)-[:a]->(v2)-[pb]->(v3)-[:c]->(v4) |
[v1, v2, v3, v4]]] +
[pa IN $pas | // r3 = Δa⋈b⋈c
[(v1)-[pa]->(v2)-[:b]->(v3)-[:c]->(v4) |
[v1, v2, v3, v4]]] AS r
RETURN
r[0] AS v1, r[1] AS v2, r[2] AS v3, r[3] AS v4](https://image.slidesharecdn.com/ocim4-ivm-180525103338/75/Incremental-View-Maintenance-for-openCypher-Queries-33-2048.jpg)
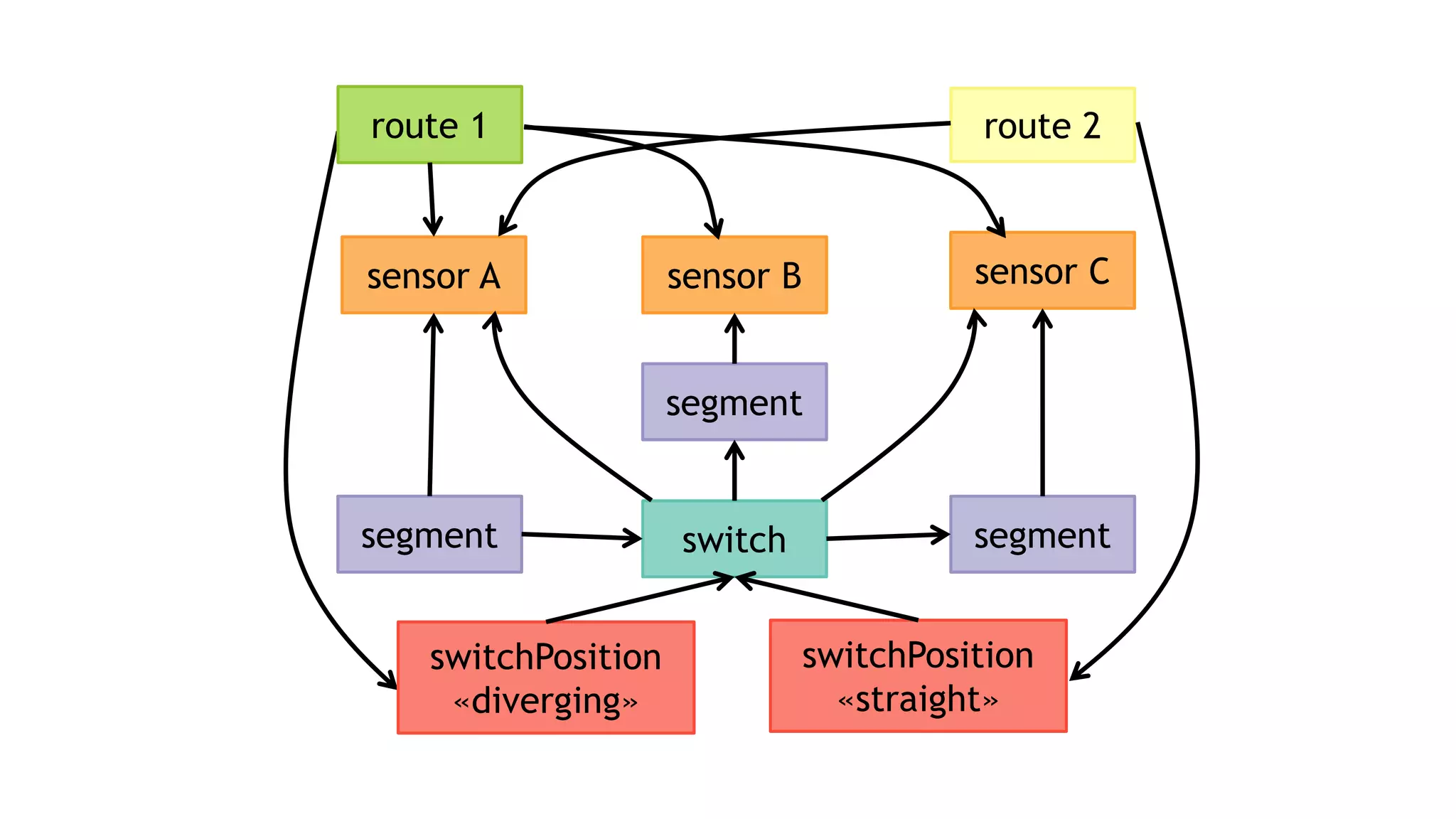
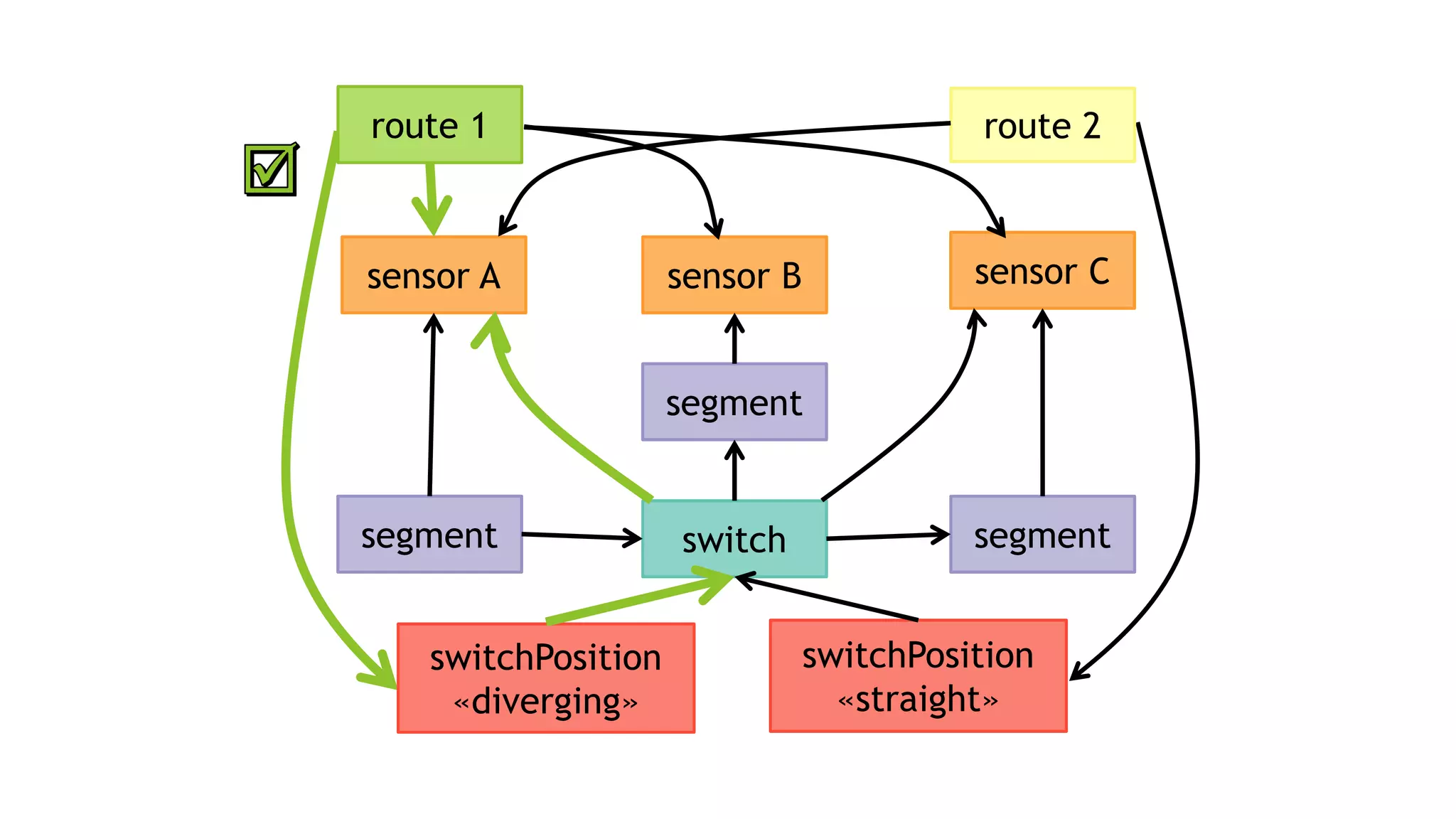
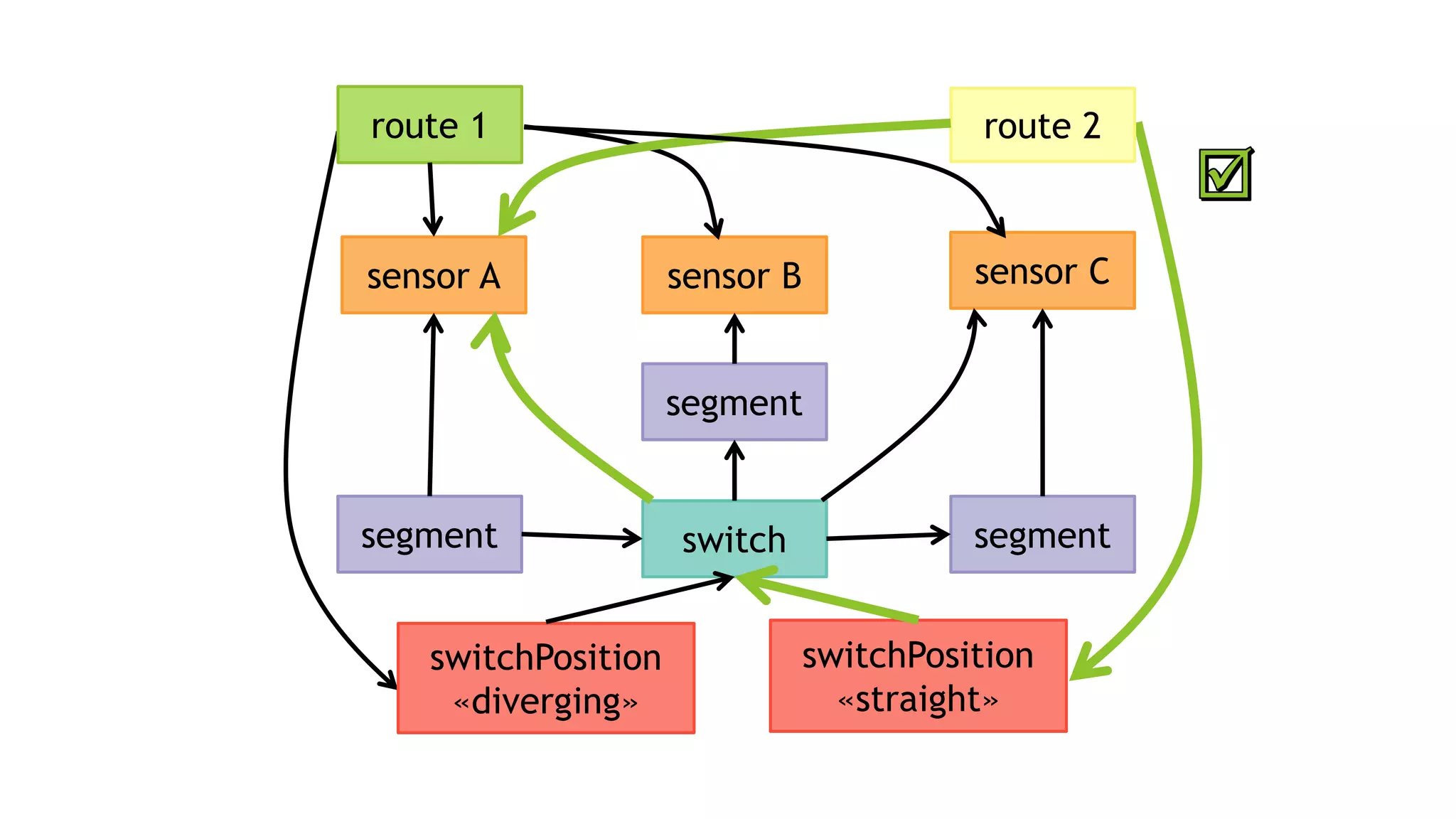
![EXAMPLE QUERY #2
MATCH (route:Route)
-[:FOLLOWS]->(swP:SwitchPosition)
-[:TARGET]->(sw:Switch)
-[:MONITORED_BY]->(sensor:Sensor)
WHERE NOT (route)-[:REQUIRES]->(sensor)
RETURN route, sensor, swP, sw
MATCH (v1)
-[:a]->(v2)
-[:b]->(v3)
-[:c]->(v4)
WHERE NOT (v1)-[:d]->(v4)
RETURN v1, v2, v3, v4
v1 v2
v3v4
:b
:c
:d
:a
:FOLLOWS
:MONITORED_BY
:TARGET:REQUIRES
sw: Switchsensor: Sensor
route: Route
swP:
SwitchPosition](https://image.slidesharecdn.com/ocim4-ivm-180525103338/75/Incremental-View-Maintenance-for-openCypher-Queries-34-2048.jpg)
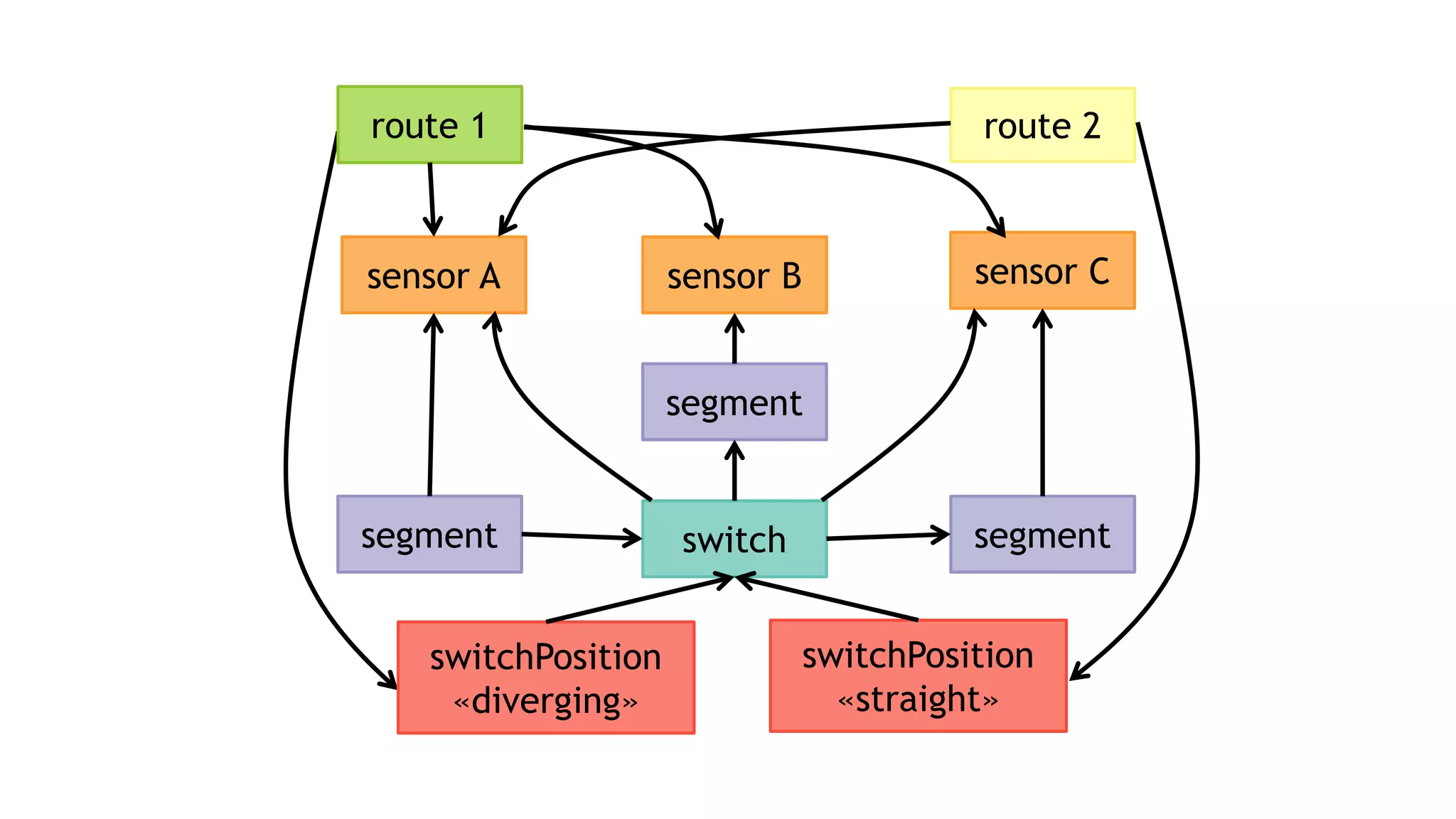
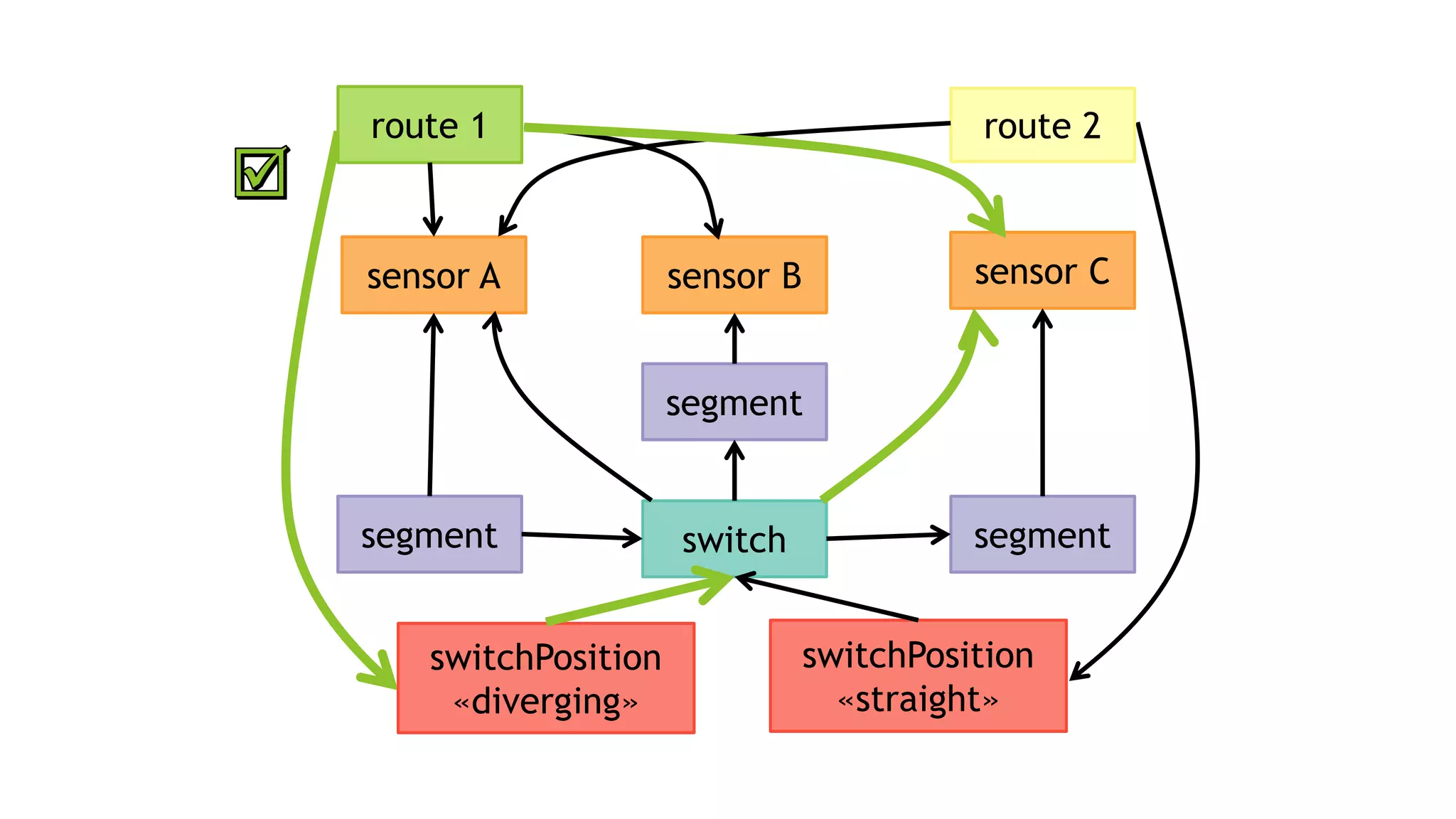
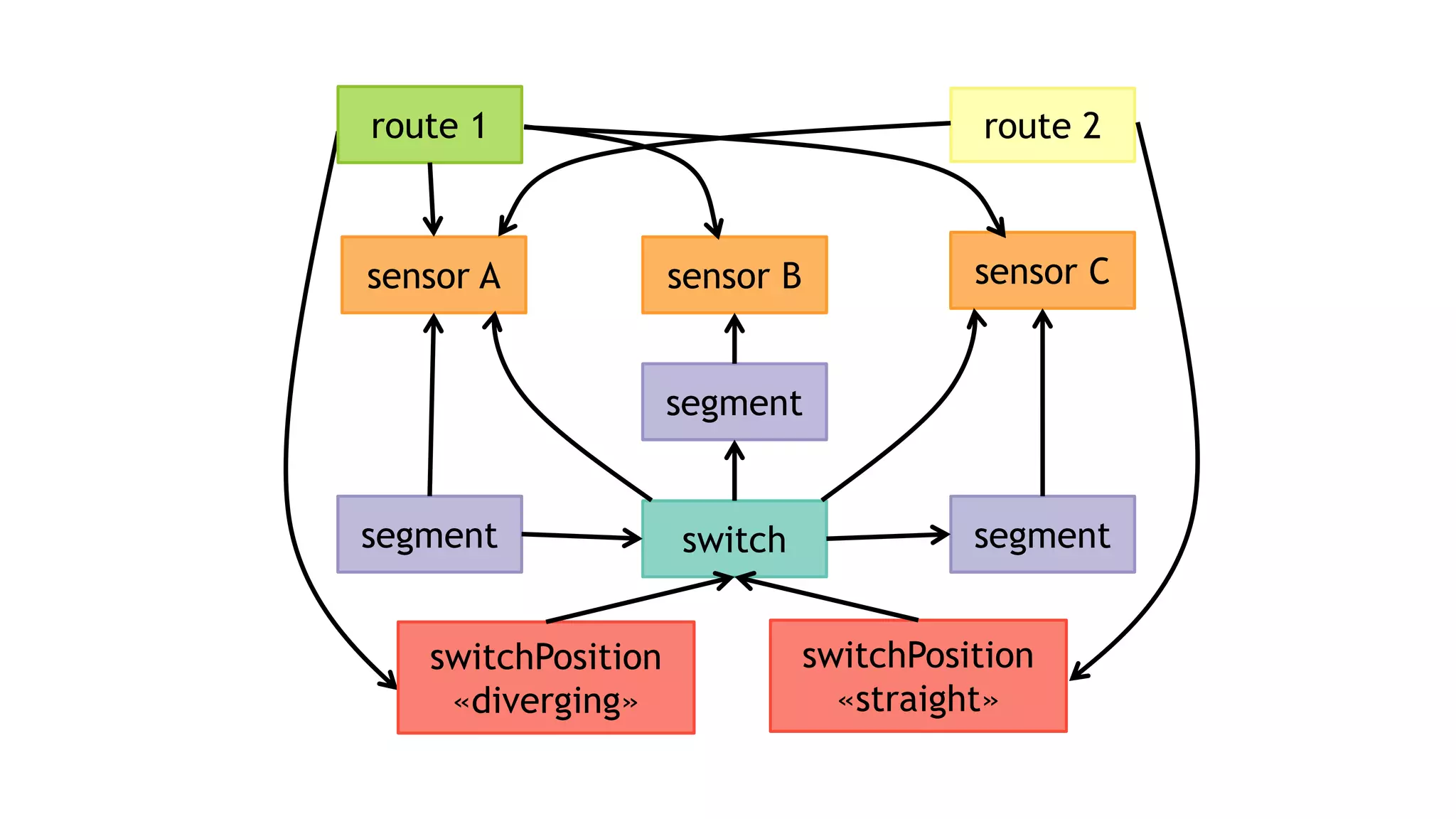
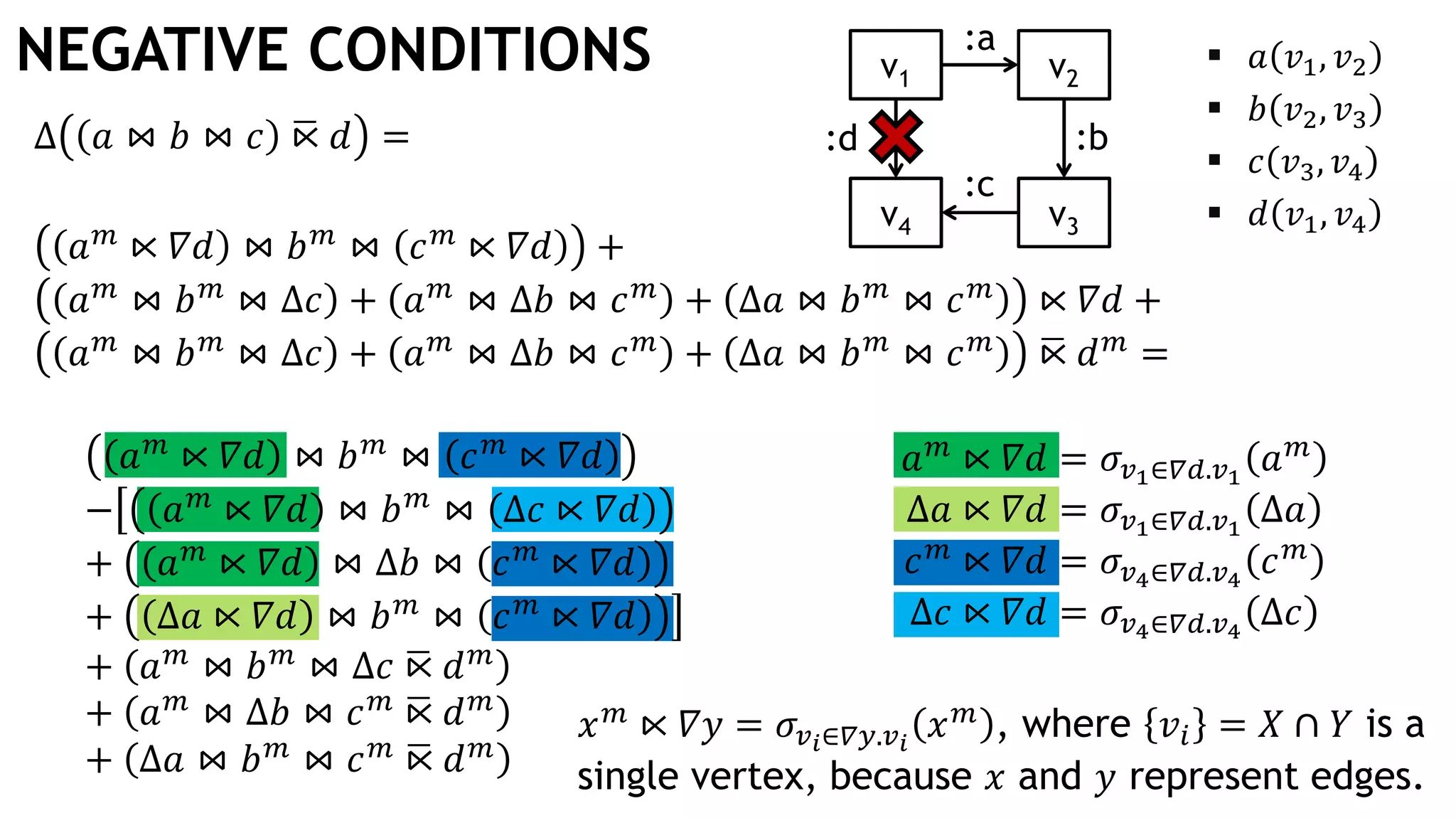
![NEGATIVE CONDITIONS
v1 v2
v3v4
:b
:c
:d
:a
MATCH (v1)
-[:a]->(v2)
-[:b]->(v3)
-[:c]->(v4)
WHERE NOT (v1)-[:d]->(v4)
RETURN v1, v2, v3, v4
𝑎 𝑣1, 𝑣2
𝑏 𝑣2, 𝑣3
𝑐 𝑣3, 𝑣4
𝑑 𝑣1, 𝑣4
⇒ 𝑎 ⋈ 𝑏 ⋈ 𝑐 ഥ⋉ 𝑑](https://image.slidesharecdn.com/ocim4-ivm-180525103338/75/Incremental-View-Maintenance-for-openCypher-Queries-35-2048.jpg)





![WITH
[] AS pes, [] AS nes
WITH
[pe IN pes WHERE type(pe) = 'a'|pe] AS pas,
[pe IN pes WHERE type(pe) = 'b'|pe] AS pbs,
[pe IN pes WHERE type(pe) = 'c'|pe] AS pcs,
[pe IN pes WHERE type(pe) = 'd'|pe] AS pds,
[ne IN nes WHERE type(ne) = 'a'|ne] AS nas,
[ne IN nes WHERE type(ne) = 'b'|ne] AS nbs,
[ne IN nes WHERE type(ne) = 'c'|ne] AS ncs,
[ne IN nes WHERE type(ne) = 'd'|ne] AS nds
WITH
pas, nas, pbs, nbs, pcs, ncs, pds, nds,
[nd IN nds | startNode(nd)] AS nd_v1s,
[nd IN nds | endNode(nd)] AS nd_v4s
// calculating s1s...s4s
// s1s: (𝑎⋉∇𝑑)
UNWIND nd_v1s AS v1
MATCH (v1)-[:a]->(v2)
WITH
pas, nas, pbs, nbs, pcs, ncs, pds, nds,
nd_v1s, nd_v4s,
collect({v1: v1, v2: v2}) AS s1s
// s2s: (Δ𝑎⋉∇𝑑)
UNWIND pas AS pa
MATCH (v1)-[pa]->(v2)
WHERE v1 IN nd_v1s
WITH
pas, nas, pbs, nbs, pcs, ncs, pds, nds,
nd_v1s, nd_v4s,
s1s,
collect({v1: v1, v2: v2}) AS s2s
// s3s: (𝑐⋉∇𝑑)
UNWIND nd_v4s AS v4
MATCH (v3)-[:c]->(v4)
WITH
pas, nas, pbs, nbs, pcs, ncs, pds, nds,
nd_v1s, nd_v4s,
s1s, s2s,note
collect({v3: v3, v4: v4}) AS s3s
// s4s: (Δ𝑐⋉∇𝑑)
UNWIND pcs AS pc
MATCH (v3)-[pc]->(v4)
WHERE v4 IN nd_v1s
WITH
pas, nas, pbs, nbs, pcs, ncs, pds, nds,
nd_v1s, nd_v4s,
s1s, s2s, s3s,
collect({v3: v3, v4: v4}) AS s4s
// calculating r1...r7
WITH
pas, nas, pbs, nbs, pcs, ncs, pds, nds,
nd_v1s, nd_v4s, s1s, s2s, s3s, s4s
// r1: (𝑎⋉∇𝑑) ⋈ 𝑏 ⋈ (𝑐⋉∇𝑑)
UNWIND s1s AS s1
UNWIND s3s AS s3
WITH
pas, nas, pbs, nbs, pcs, ncs, pds, nds,
nd_v1s, nd_v4s, s1s, s2s, s3s, s4s,
s1.v1 AS v1, s1.v2 AS v2, s3.v3 AS v3, s3.v4
AS v4
WHERE (v2)-[:b]->(v3)
WITH
pas, nas, pbs, nbs, pcs, ncs, pds, nds,
nd_v1s, nd_v4s, s1s, s2s, s3s, s4s,
collect([v1, v2, v3, v4]) AS r1
// r2: -(𝑎⋉∇𝑑) ⋈ 𝑏 ⋈ (Δ𝑐⋉∇𝑑)
UNWIND s1s AS s1
UNWIND s4s AS s4
WITH
pas, nas, pbs, nbs, pcs, ncs, pds, nds,
nd_v1s, nd_v4s, s1s, s2s, s3s, s4s,
r1,
s1.v1 AS v1, s1.v2 AS v2, s4.v3 AS v3, s4.v4
AS v4
WHERE (v2)-[:b]->(v3)
WITH
pas, nas, pbs, nbs, pcs, ncs, pds, nds,
nd_v1s, nd_v4s, s1s, s2s, s3s, s4s,
r1,
collect([v1, v2, v3, v4]) AS r2
// r3: -(𝑎⋉∇𝑑) ⋈ Δ𝑏 ⋈ (𝑐⋉∇𝑑)
UNWIND s1s AS s1
UNWIND s3s AS s3
WITH
pas, nas, pbs, nbs, pcs, ncs, pds, nds,
nd_v1s, nd_v4s, s1s, s2s, s3s, s4s,
r1, r2,
s1.v1 AS v1, s1.v2 AS v2, s3.v3 AS v3, s3.v4
AS v4
MATCH (v2)-[b:b]->(v3)
WHERE b IN pbs
WITH
pas, nas, pbs, nbs, pcs, ncs, pds, nds,
nd_v1s, nd_v4s, s1s, s2s, s3s, s4s,
r1, r2,
collect([v1, v2, v3, v4]) AS r3
// r4: -(Δ𝑎⋉∇𝑑) ⋈ 𝑏 ⋈ (𝑐⋉∇𝑑)
UNWIND s2s AS s2
UNWIND s3s AS s3
WITH
pas, nas, pbs, nbs, pcs, ncs, pds, nds,
nd_v1s, nd_v4s, s1s, s2s, s3s, s4s,
r1, r2, r3,
s2.v1 AS v1, s2.v2 AS v2, s3.v3 AS v3, s3.v4
AS v4
MATCH (v2)-[b:b]->(v3)
WHERE b IN pbs
WITH
pas, nas, pbs, nbs, pcs, ncs, pds, nds,
nd_v1s, nd_v4s, s1s, s2s, s3s, s4s,
r1, r2, r3,
collect([v1, v2, v3, v4]) AS r4
// r5: 𝑎 ⋈ 𝑏 ⋈ Δ𝑐 ̅⋉ 𝑑
UNWIND pcs AS pc
MATCH (v1)-[:a]->(v2)-[:b]->(v3)-[:pc]->(v4)
WHERE NOT (v1)-[:d]->(v4)
WITH
pas, nas, pbs, nbs, pcs, ncs, pds, nds,
nd_v1s, nd_v4s, s1s, s2s, s3s, s4s,
r1, r2, r3, r4,
collect([v1, v2, v3, v4]) AS r5
// r6: 𝑎 ⋈ Δ𝑏 ⋈ 𝑐 ̅⋉ 𝑑
UNWIND pbs AS pb
MATCH (v1)-[:a]->(v2)-[:pb]->(v3)-[:c]->(v4)
WHERE NOT (v1)-[:d]->(v4)
WITH
pas, nas, pbs, nbs, pcs, ncs, pds, nds,
nd_v1s, nd_v4s, s1s, s2s, s3s, s4s,
r1, r2, r3, r4, r5,
collect([v1, v2, v3, v4]) AS r6
// r7: Δ𝑎 ⋈ 𝑏 ⋈ 𝑐 ̅⋉ 𝑑
UNWIND pas AS pa
MATCH (v1)-[:pa]->(v2)-[:b]->(v3)-[:c]->(v4)
WHERE NOT (v1)-[:d]->(v4)
WITH
pas, nas, pbs, nbs, pcs, ncs, pds, nds,
nd_v1s, nd_v4s, s1s, s2s, s3s, s4s,
r1, r2, r3, r4, r5, r6,
collect([v1, v2, v3, v4]) AS r7
WITH
r1 + r5 + r6 + r7 AS rp,
r2 + r3 + r4 AS rn
RETURN
[r IN rp WHERE NOT r IN rn] AS results
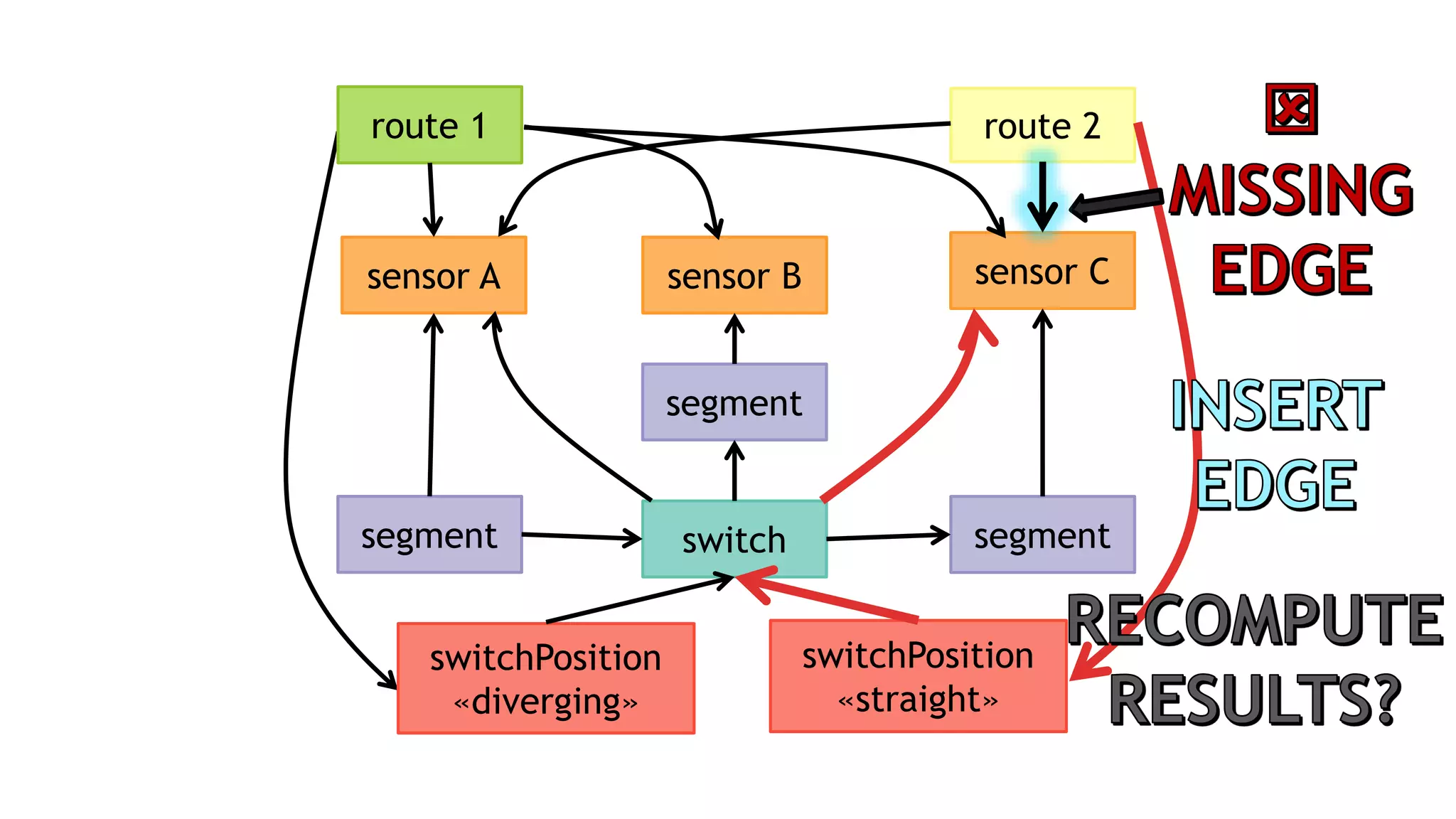
POSITIVE DELTA QUERY FOR 𝑎 ⋈ 𝑏 ⋈ 𝑐 ഥ⋉ 𝑑](https://image.slidesharecdn.com/ocim4-ivm-180525103338/75/Incremental-View-Maintenance-for-openCypher-Queries-42-2048.jpg)
![POSITIVE DELTA QUERY FOR 𝑎 ⋈ 𝑏 ⋈ 𝑐 ഥ⋉ 𝑑
Workaround: knowing the change workload helps
o Only consider changes in Δ𝑑 and 𝛻𝑑
o Query is cleaner and much more efficient
UNWIND $nds AS nd
WITH
startNode(nd) AS v1,
endNode(nd) AS v4
MATCH (v1)-[:a]->(v2)-[:b]->(v3)-[:c]->(v4)
RETURN v1, v2, v3, v4
This can outperform recomputing the query from scratch.](https://image.slidesharecdn.com/ocim4-ivm-180525103338/75/Incremental-View-Maintenance-for-openCypher-Queries-43-2048.jpg)
![LIST OPERATIONS IN CYPHER
Instead of subqueries, use chained queries and combine lists.
WITH [1, 1, 2, 2, 3] AS xs
UNWIND xs AS x
RETURN
collect(DISTINCT x) AS unique
WITH [1, 2, 3] AS xs, [2] AS ys
RETURN
xs + ys AS append,
[x IN xs WHERE NOT x IN ys] AS subtraction,
[x IN xs WHERE x IN ys] AS intersection
WITH [1, 1, 2, 2, 3] AS xs
RETURN
reduce(acc = [], x in xs |
acc + CASE x IN acc
WHEN false THEN [x]
ELSE []
END) AS unique
Get unique list in openCypher](https://image.slidesharecdn.com/ocim4-ivm-180525103338/75/Incremental-View-Maintenance-for-openCypher-Queries-44-2048.jpg)
![DELTA QUERIES IN CYPHER
Delta queries are complex. Features that would be nice:
Subqueries //pattern comprehensions go some length
Named subqueries //help reusability
Subtracting lists //related: CIR-2017-180
Use collection elements or function results for matching
These are probably too much to ask.
-> recommended approach: compile directly to query plans.
MATCH (n)
WITH collect(n) AS ns
MATCH (ns[0])
RETURN *
MATCH (n)
WITH collect(n) AS ns
WITH ns[0] AS x
MATCH (x)
RETURN *
](https://image.slidesharecdn.com/ocim4-ivm-180525103338/75/Incremental-View-Maintenance-for-openCypher-Queries-45-2048.jpg)