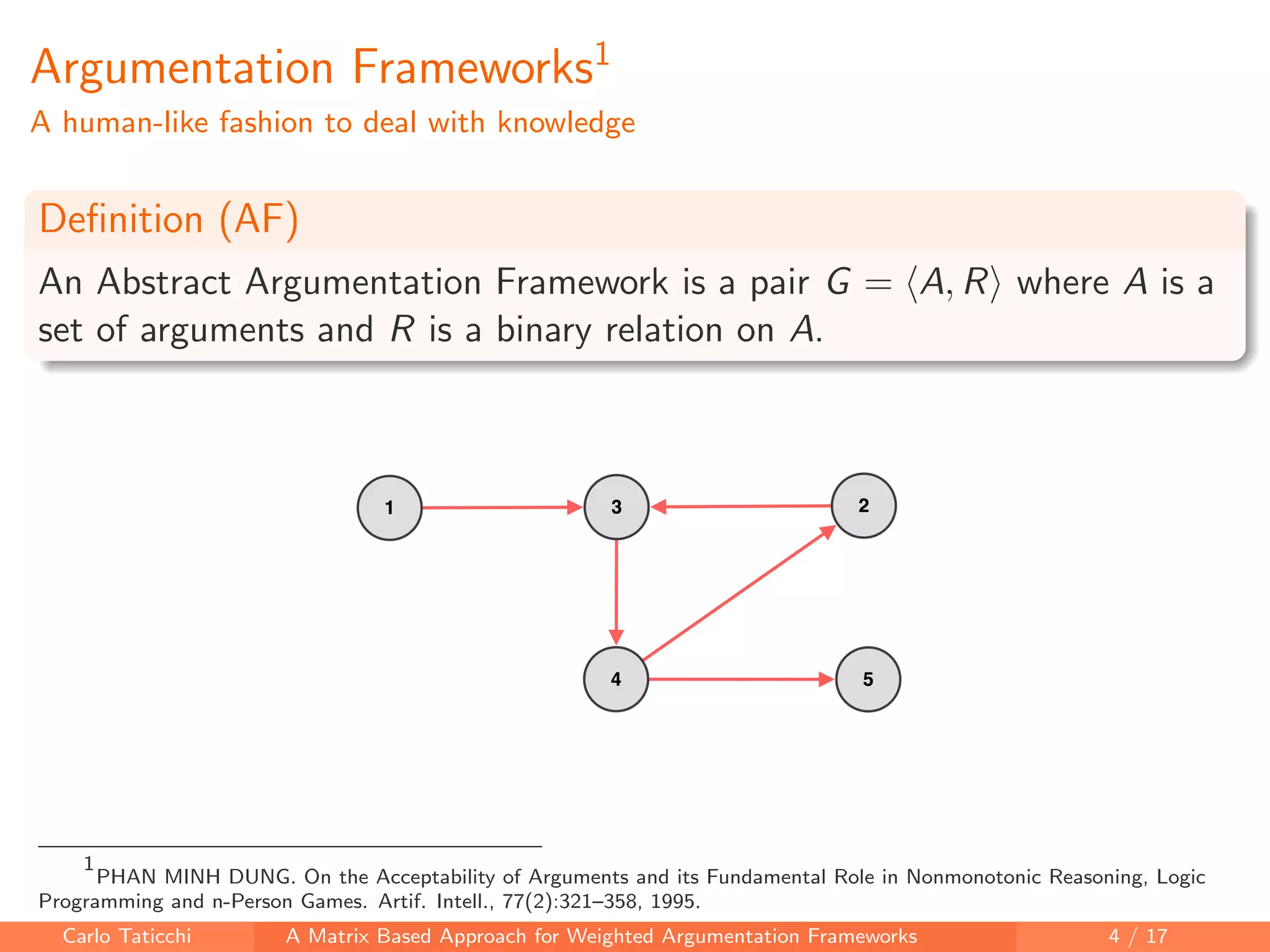
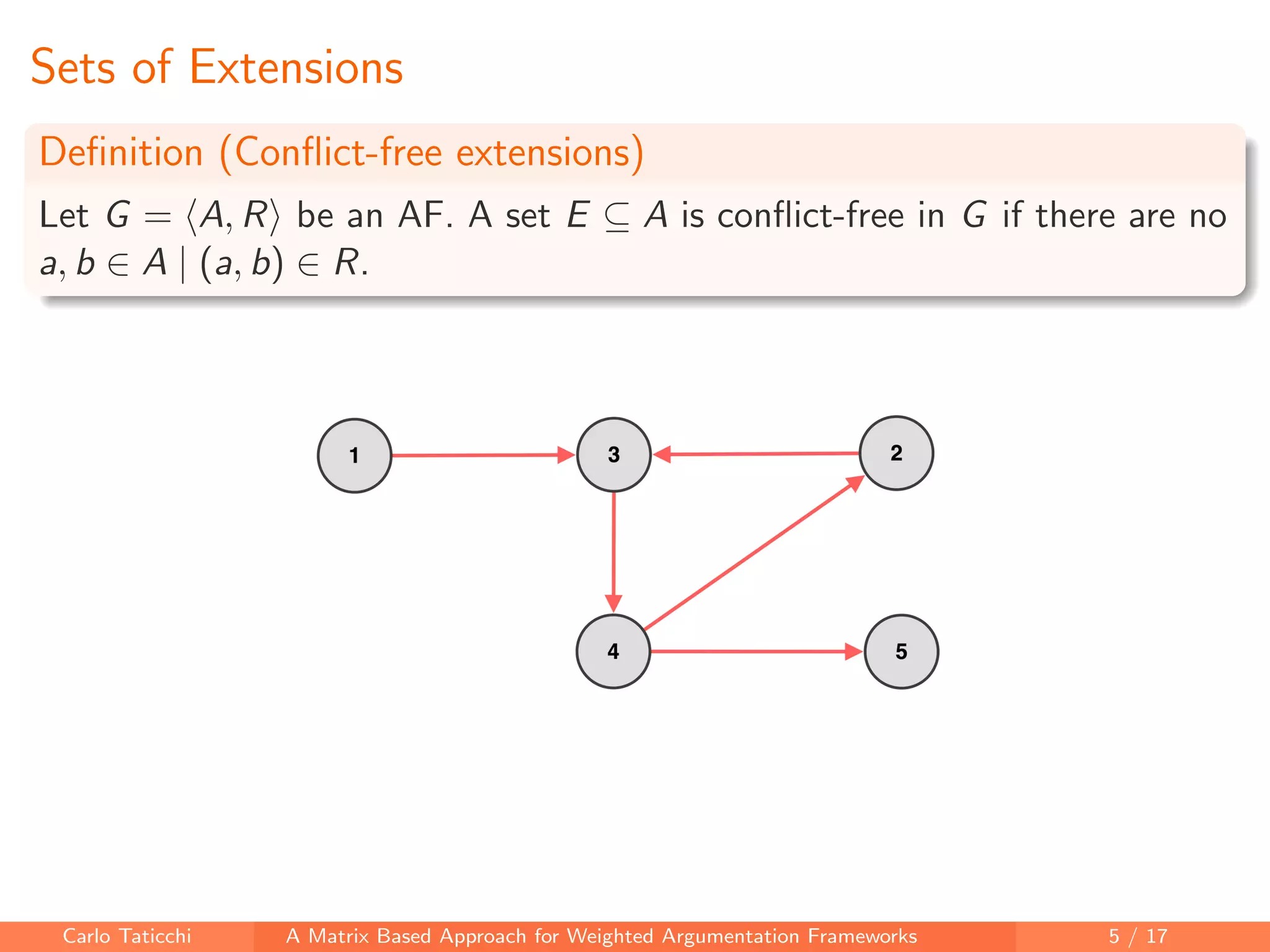
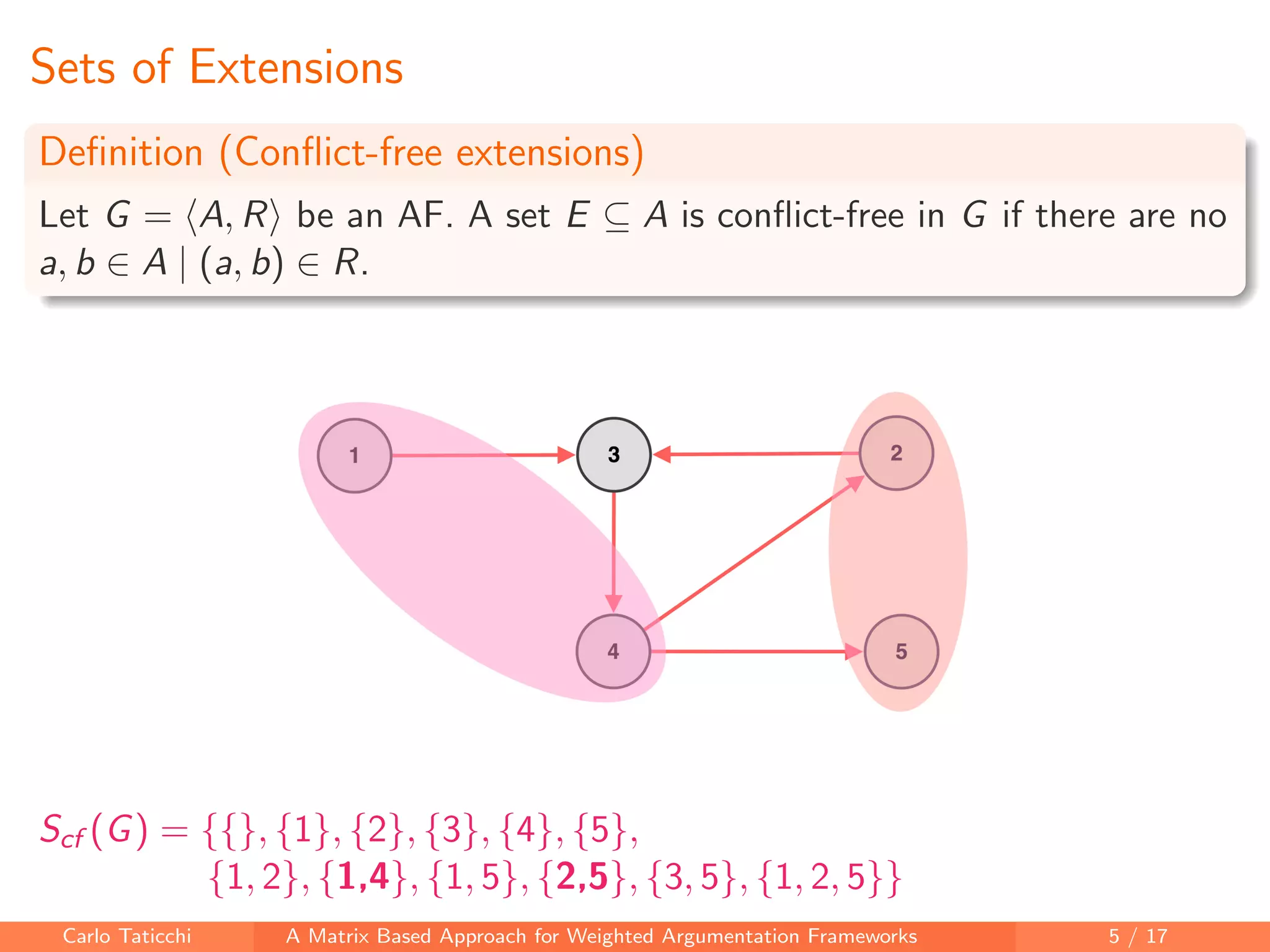
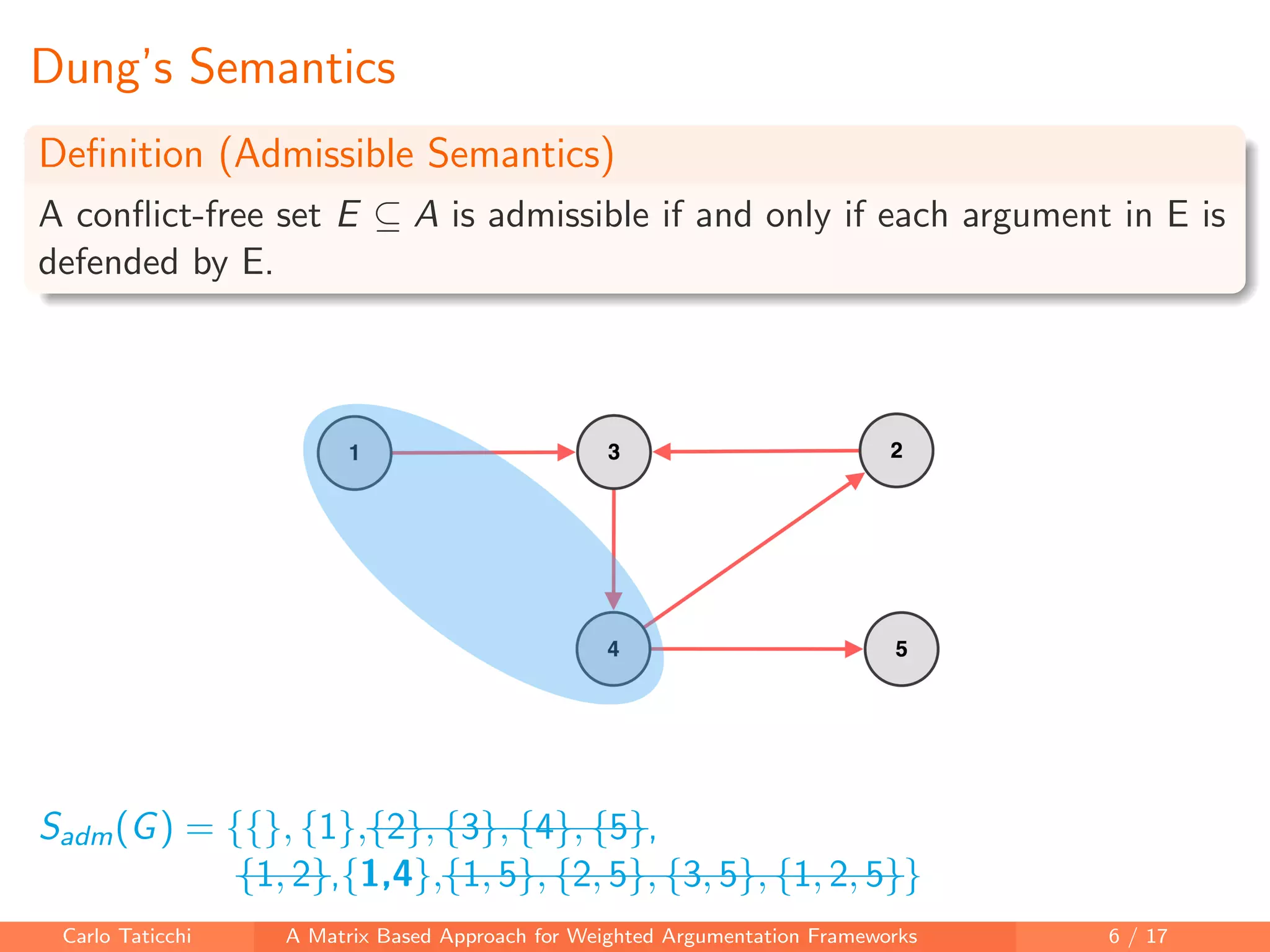
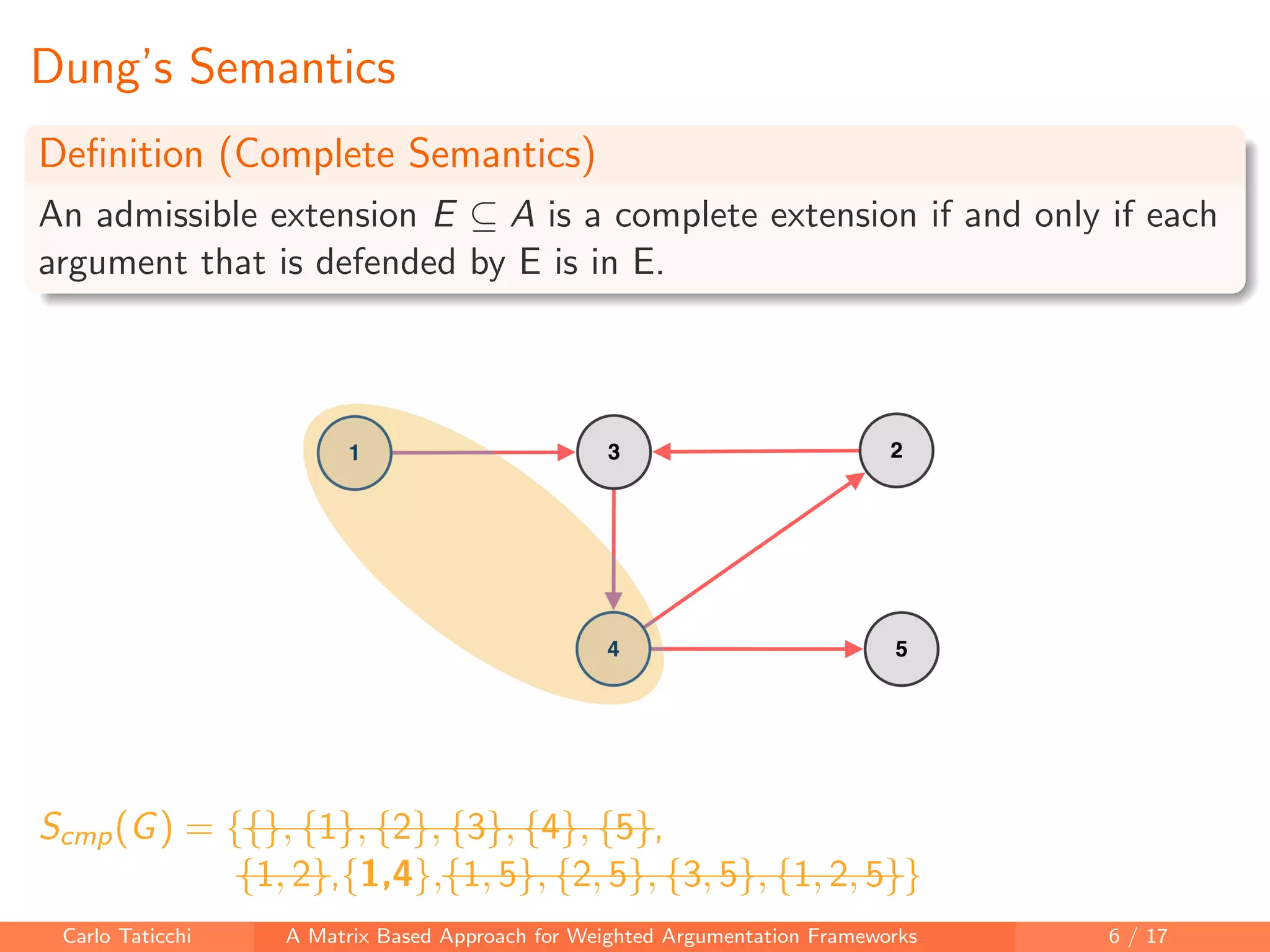
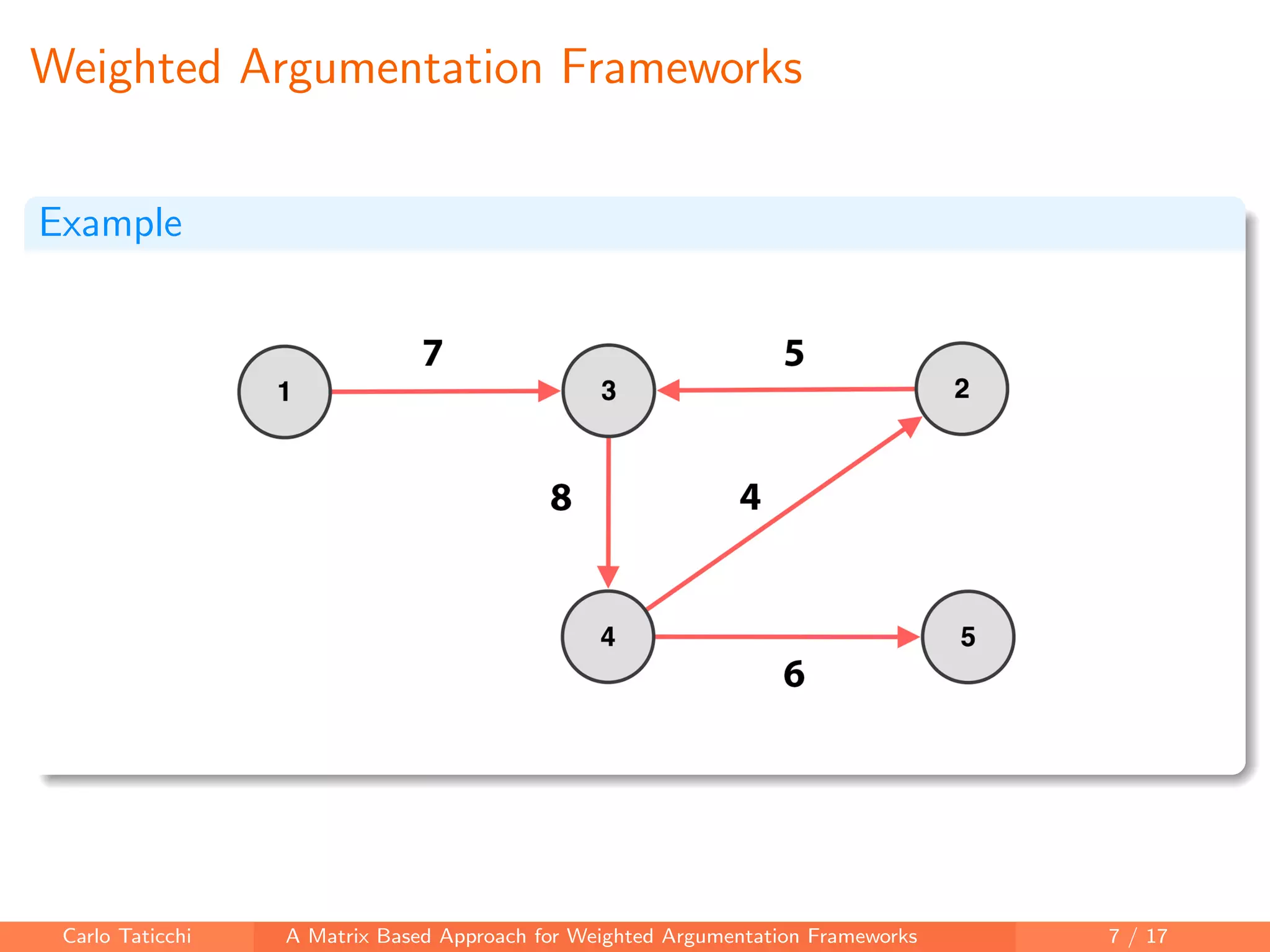
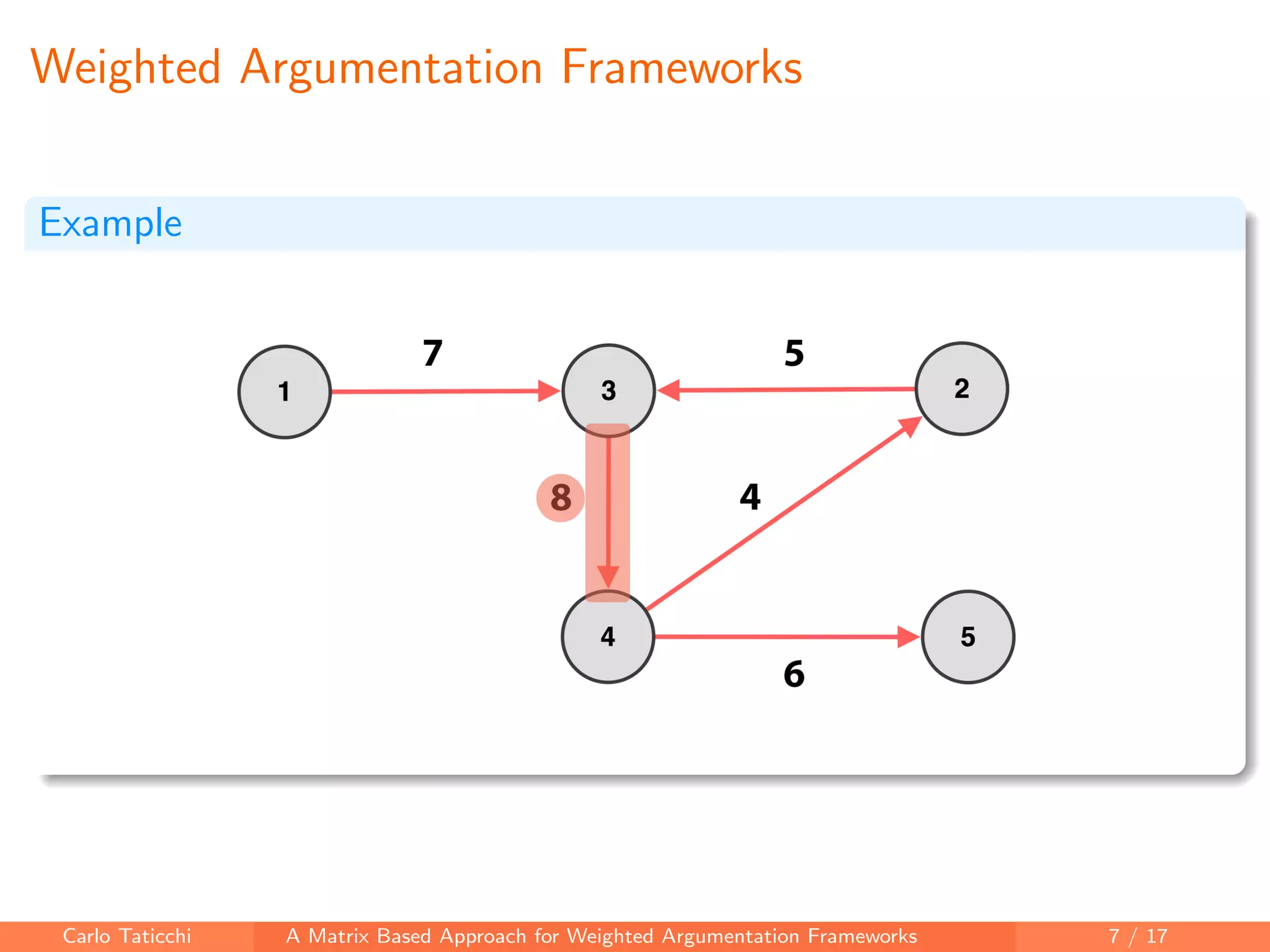
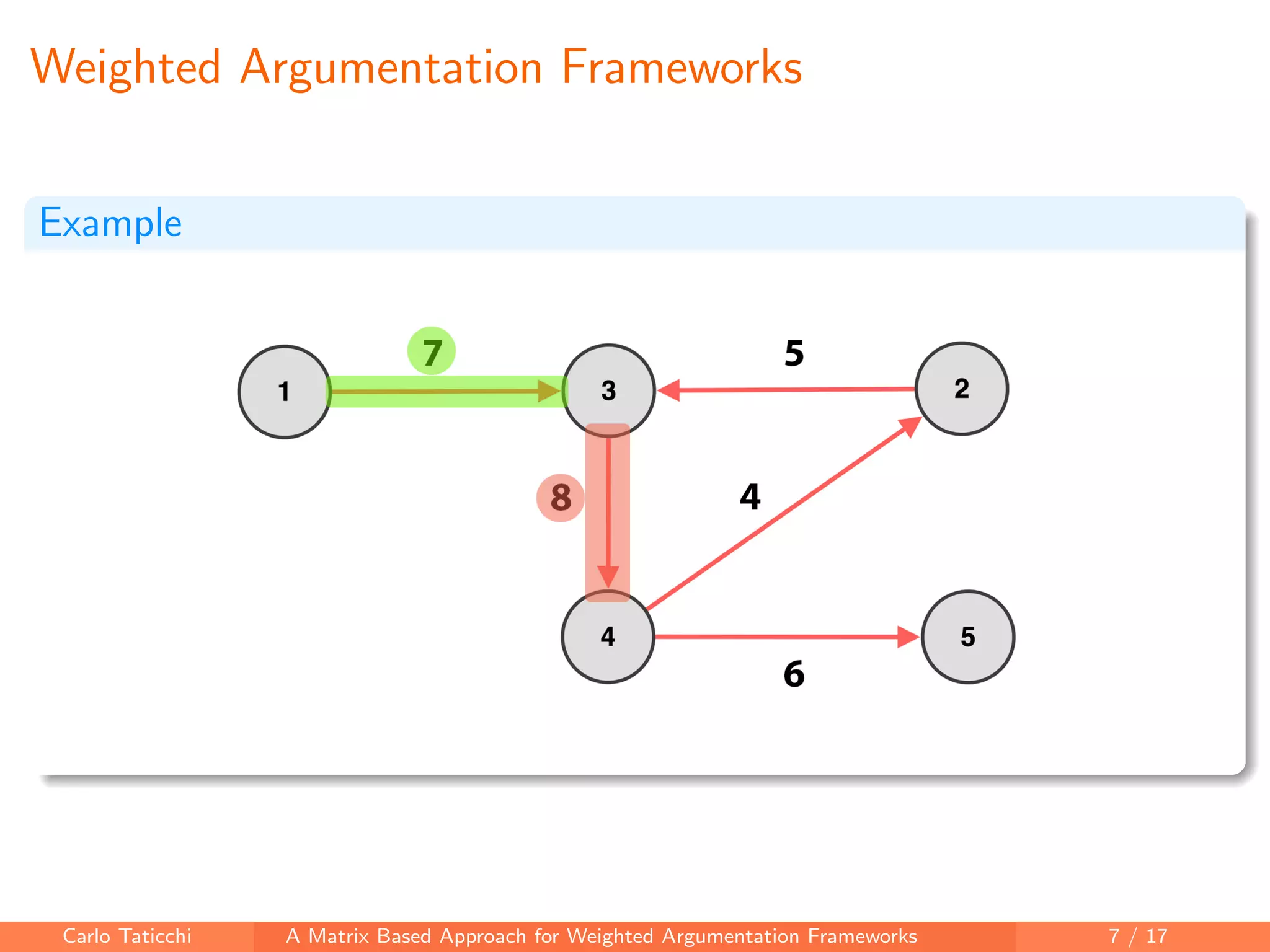
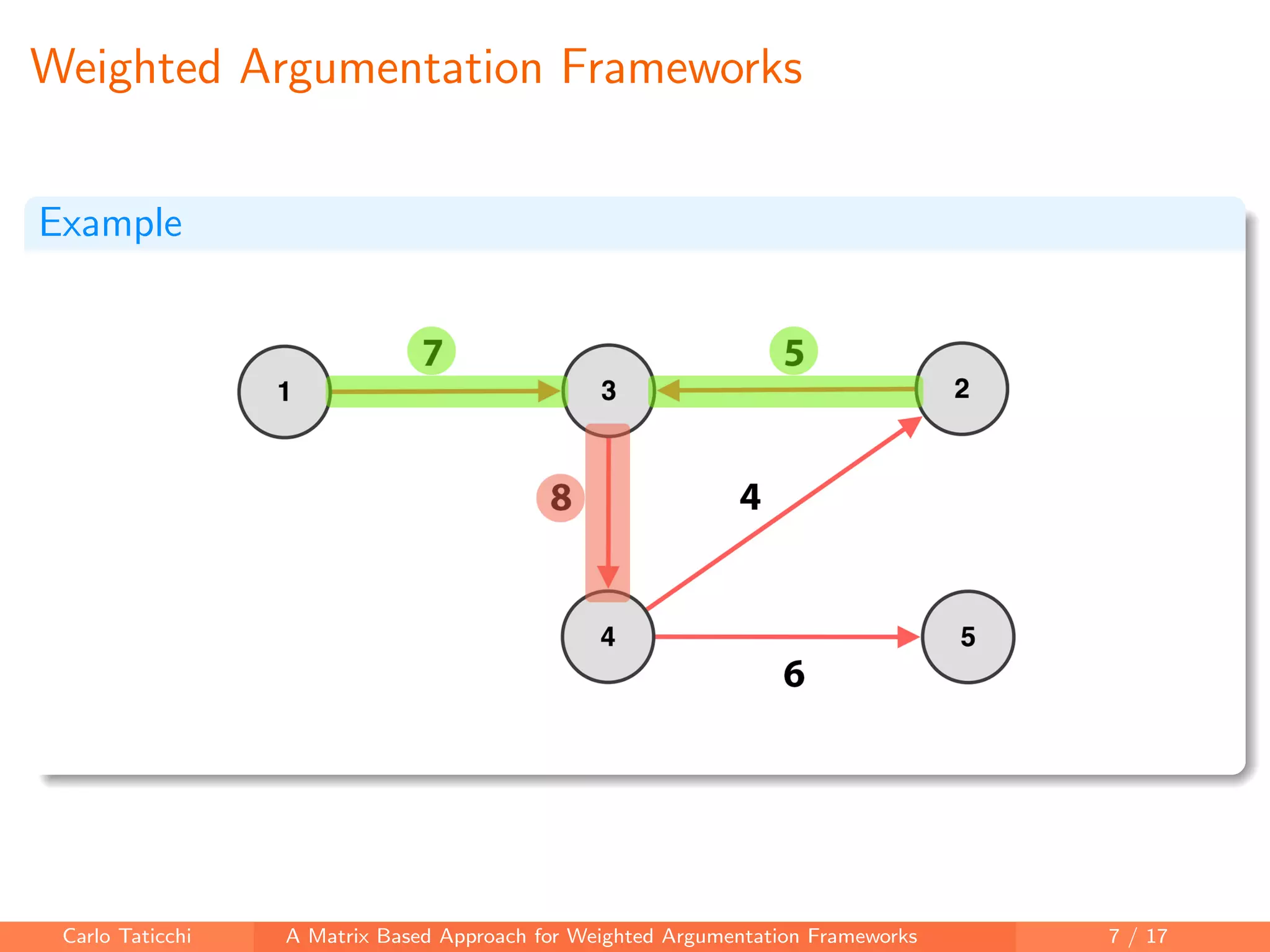
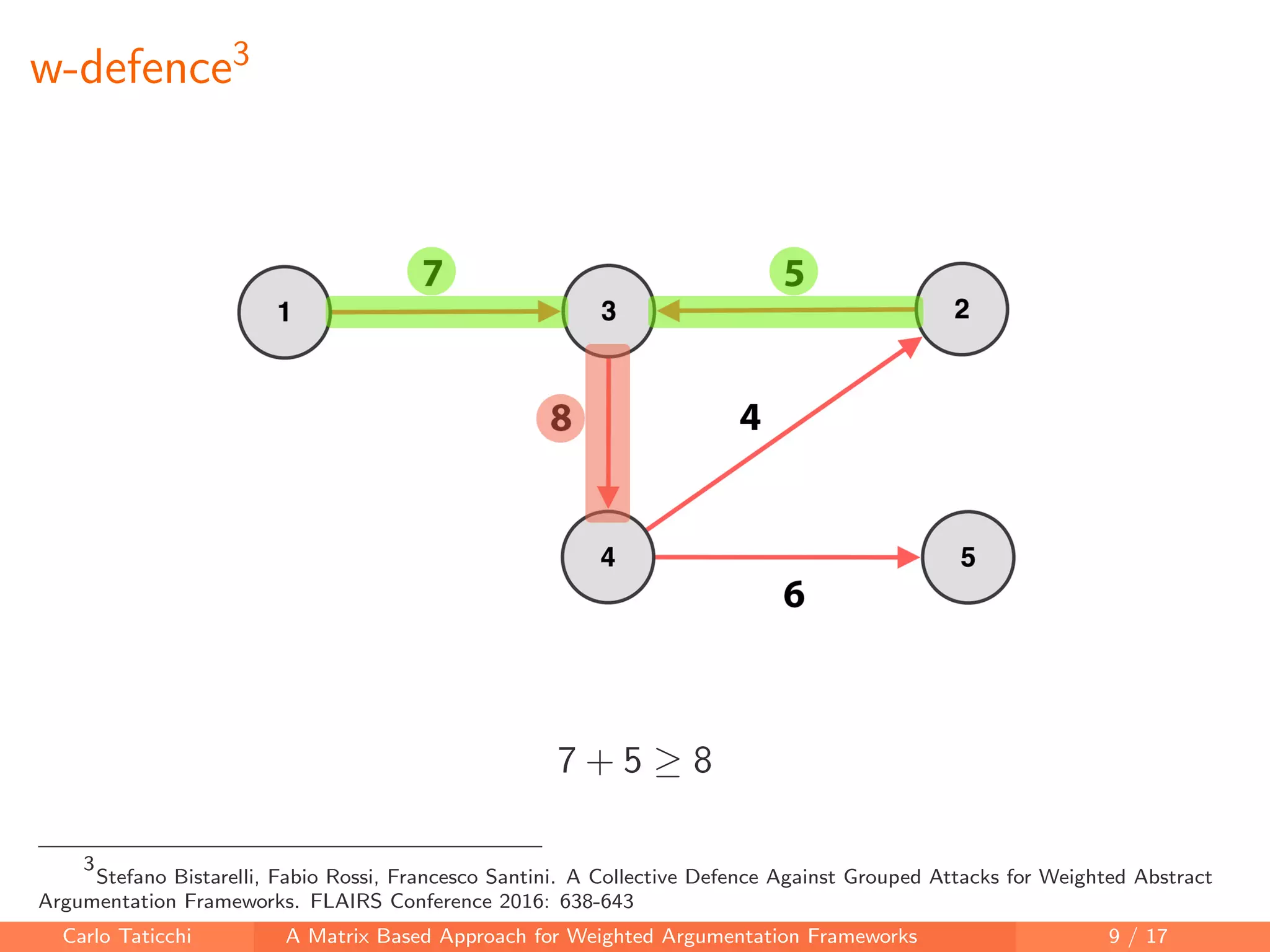
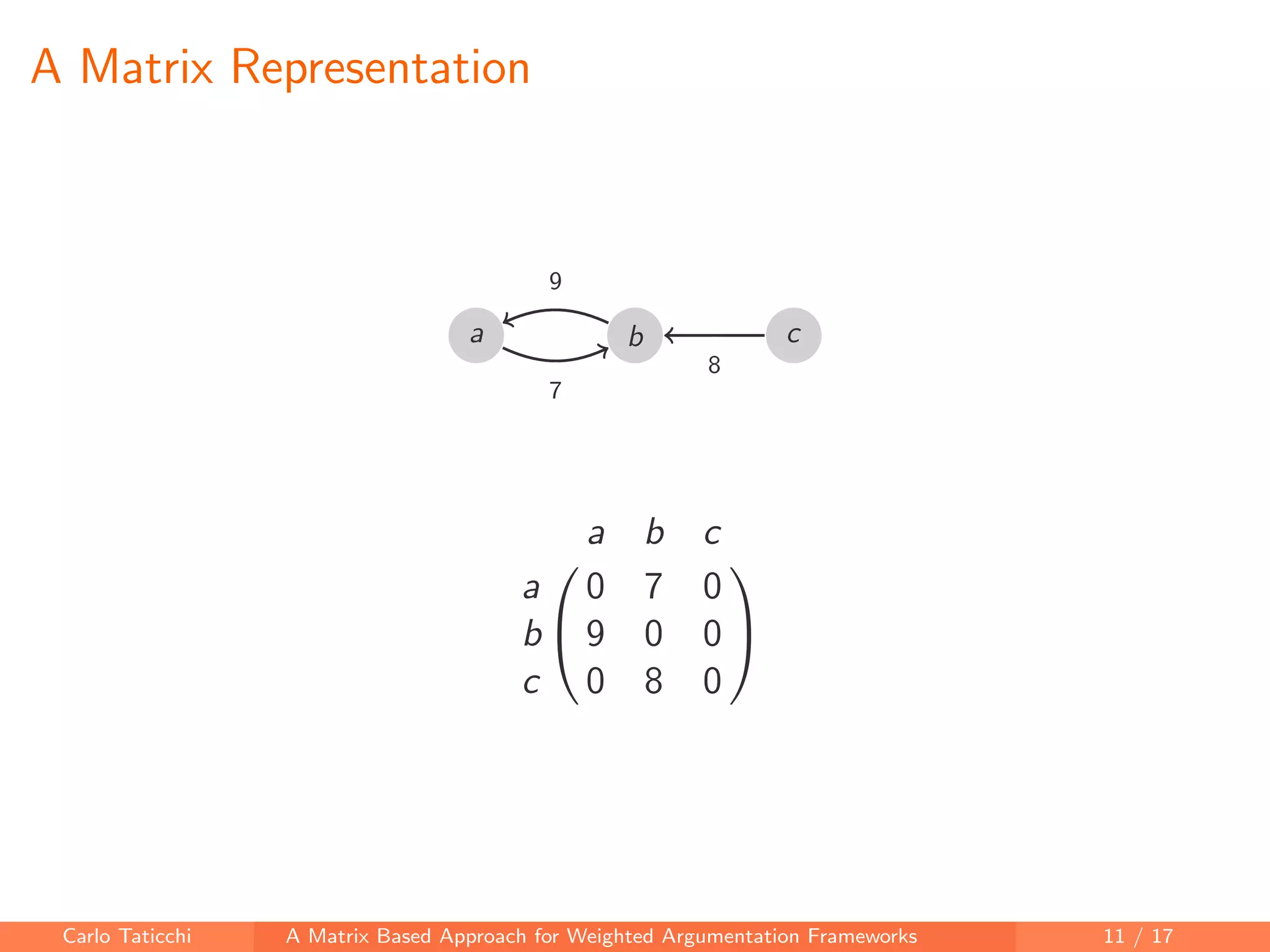
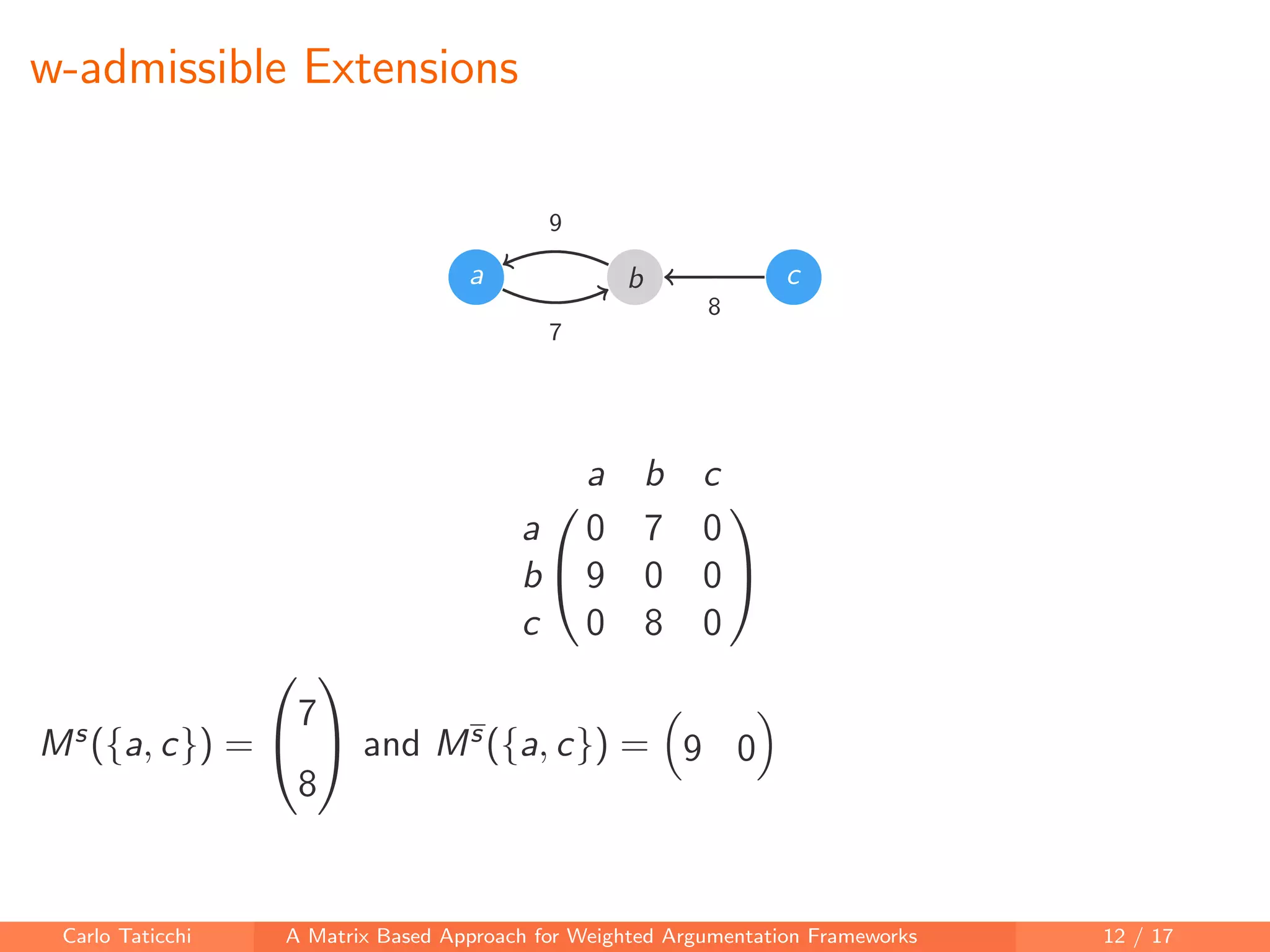
The document presents a matrix-based approach for analyzing weighted argumentation frameworks, focusing on extensions and various semantics such as admissible and complete semantics. It highlights methods for reducing the size of argumentation frameworks and discusses proposed future work, including extending existing systems and testing the advantages of reduction techniques. The authors aim to provide a structured computational framework for evaluating argument acceptability in nonmonotonic reasoning.

1. A Matrix Based Approach for
Weighted Argumentation Frameworks
Stefano Bistarelli1 Alessandra Tappini1 Carlo Taticchi2
stefano.bistarelli@unipg.it alessandra.tappini@unipg.it carlo.taticchi@gssi.it
1Universit`a degli Studi di Perugia, Italy
2Gran Sasso Science Institute (GSSI), L’Aquila, Italy

5. Index
1 Background - Argumentation Frameworks
2 A Matrix Representation for Weighted AFs
3 Reducing the Size of an AF
4 Conclusion and Future Work
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 3 / 17

6. Argumentation Frameworks1
A human-like fashion to deal with knowledge
Definition (AF)
An Abstract Argumentation Framework is a pair G = A, R where A is a
set of arguments and R is a binary relation on A.
1
PHAN MINH DUNG. On the Acceptability of Arguments and its Fundamental Role in Nonmonotonic Reasoning, Logic
Programming and n-Person Games. Artif. Intell., 77(2):321–358, 1995.
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 4 / 17

7. Sets of Extensions
Definition (Conflict-free extensions)
Let G = A, R be an AF. A set E ⊆ A is conflict-free in G if there are no
a, b ∈ A | (a, b) ∈ R.
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 5 / 17

8. Sets of Extensions
Definition (Conflict-free extensions)
Let G = A, R be an AF. A set E ⊆ A is conflict-free in G if there are no
a, b ∈ A | (a, b) ∈ R.
Scf (G) = {{}, {1}, {2}, {3}, {4}, {5},
{1, 2}, {1,4}, {1, 5}, {2,5}, {3, 5}, {1, 2, 5}}
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 5 / 17

9. Dung’s Semantics
Definition (Admissible Semantics)
A conflict-free set E ⊆ A is admissible if and only if each argument in E is
defended by E.
Sadm(G) = {{}, {1},{2}, {3}, {4}, {5},
{1, 2},{1,4},{1, 5}, {2, 5}, {3, 5}, {1, 2, 5}}
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 6 / 17

10. Dung’s Semantics
Definition (Complete Semantics)
An admissible extension E ⊆ A is a complete extension if and only if each
argument that is defended by E is in E.
Scmp(G) = {{}, {1}, {2}, {3}, {4}, {5},
{1, 2},{1,4},{1, 5}, {2, 5}, {3, 5}, {1, 2, 5}}
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 6 / 17

11. Weighted Argumentation Frameworks
Example
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 7 / 17

12. Weighted Argumentation Frameworks
Example
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 7 / 17

13. Weighted Argumentation Frameworks
Example
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 7 / 17

14. Weighted Argumentation Frameworks
Example
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 7 / 17

15. Semiring-based WAF2
• WAFS : A, R, W , S
• S : S, ⊕, ⊗, ⊥,
• Sweighted = R+ ∪ {+∞}, min, +, +∞, 0
• W (B, D) =
b∈B,d∈D
W (b, d)
2
Stefano Bistarelli, Francesco Santini. A Common Computational Framework for Semiring-based Argumentation Systems.
ECAI 2010: 131-136.
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 8 / 17

16. Semiring-based WAF2
• WAFS : A, R, W , S
• S : S, ⊕, ⊗, ⊥,
• Sweighted = R+ ∪ {+∞}, min, +, +∞, 0
• W (B, D) =
b∈B,d∈D
W (b, d)
2
Stefano Bistarelli, Francesco Santini. A Common Computational Framework for Semiring-based Argumentation Systems.
ECAI 2010: 131-136.
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 8 / 17

17. Semiring-based WAF2
• WAFS : A, R, W , S
• S : S, ⊕, ⊗, ⊥,
• Sweighted = R+ ∪ {+∞}, min, +, +∞, 0
• W (B, D) =
b∈B,d∈D
W (b, d)
2
Stefano Bistarelli, Francesco Santini. A Common Computational Framework for Semiring-based Argumentation Systems.
ECAI 2010: 131-136.
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 8 / 17

18. Semiring-based WAF2
• WAFS : A, R, W , S
• S : S, ⊕, ⊗, ⊥,
• Sweighted = R+ ∪ {+∞}, min, +, +∞, 0
• W (B, D) =
b∈B,d∈D
W (b, d)
2
Stefano Bistarelli, Francesco Santini. A Common Computational Framework for Semiring-based Argumentation Systems.
ECAI 2010: 131-136.
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 8 / 17

19. w-defence3
7 + 5 ≥ 8
3
Stefano Bistarelli, Fabio Rossi, Francesco Santini. A Collective Defence Against Grouped Attacks for Weighted Abstract
Argumentation Frameworks. FLAIRS Conference 2016: 638-643
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 9 / 17

20. A Matrix Approach
for Computing Extensions

21. A Matrix Representation
a b c
7
9
8


a b c
a 0 7 0
b 9 0 0
c 0 8 0


Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 11 / 17

22. w-admissible Extensions
a b c
7
9
8


a b c
a 0 7 0
b 9 0 0
c 0 8 0


Ms({a, c}) =


7
8

 and Ms({a, c}) = 9 0
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 12 / 17

23. w-admissible Extensions
a b c
7
9
8


a b c
a 0 7 0
b 9 0 0
c 0 8 0


Ms({a, c}) =


7
8

 and Ms({a, c}) = 9 0 {a, c} is w-admissible
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 12 / 17

24. w-complete Extensions
a
b c
d
4
8
3




a b c d
a 0 4 0 0
b 0 0 8 0
c 0 0 0 0
d 0 3 0 0




Ms({a, d}) =


4 0
3 0

 and Mc({a, d}) =


0 8
0 0


Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 13 / 17

25. w-complete Extensions
a
b c
d
4
8
3




a b c d
a 0 4 0 0
b 0 0 8 0
c 0 0 0 0
d 0 3 0 0




Ms({a, d}) =


4 0
3 0

 and Mc({a, d}) =


0 8
0 0

 {a, d} is w-complete
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 13 / 17

26. Reduction by Contraction
a b c
7
9
8
Example


a b c
a 0 7 0
b 9 0 0
c 0 8 0

 becomes
a b
a 0 7 + 8
b 9 0
• a = {a} ∪ {c}
• {a, c} is w-admissible iff {a } is w-admissible
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 14 / 17

27. Reduction by Contraction
a b c
7
9
8
Example


a b c
a 0 7 0
b 9 0 0
c 0 8 0

 becomes
a b
a 0 7 + 8
b 9 0
• a = {a} ∪ {c}
• {a, c} is w-admissible iff {a } is w-admissible
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 14 / 17

28. Reduction by Contraction
a b c
7
9
8
Example


a b c
a 0 7 0
b 9 0 0
c 0 8 0

 becomes
a b
a 0 7 + 8
b 9 0
• a = {a} ∪ {c}
• {a, c} is w-admissible iff {a } is w-admissible
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 14 / 17

29. Reduction by Division
for w-grounded and w-preferred extensions
a b
c
d
5
2
8
Build w-grounded
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 15 / 17

30. Reduction by Division
for w-grounded and w-preferred extensions
a b
c
a b
d
5
2
8
Build w-grounded
{a}
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 15 / 17

31. Reduction by Division
for w-grounded and w-preferred extensions
a b
c
a b
c
d
5
2
8
Build w-grounded
{a} ∪ {c}
Theorem
The union of non conflicting w-admissible extensions is w-admissible.
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 15 / 17

32. Conclusion
• Matrix approach for studying extensions of semiring-based semantics.
• Check if a set of arguments is an extension for some semantics.
• Reduce the number of arguments of a WAF.
• Incremental procedure for w-grounded and w-preferred extensions.
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 16 / 17

33. Conclusion
• Matrix approach for studying extensions of semiring-based semantics.
• Check if a set of arguments is an extension for some semantics.
• Reduce the number of arguments of a WAF.
• Incremental procedure for w-grounded and w-preferred extensions.
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 16 / 17

34. Conclusion
• Matrix approach for studying extensions of semiring-based semantics.
• Check if a set of arguments is an extension for some semantics.
• Reduce the number of arguments of a WAF.
• Incremental procedure for w-grounded and w-preferred extensions.
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 16 / 17

35. Conclusion
• Matrix approach for studying extensions of semiring-based semantics.
• Check if a set of arguments is an extension for some semantics.
• Reduce the number of arguments of a WAF.
• Incremental procedure for w-grounded and w-preferred extensions.
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 16 / 17

36. Future Work
• Extend ConArg4 with the matrix approach.
• Test the real advantages of the reduction.
• Consider coalitions of arguments5.
4
http://www.dmi.unipg.it/conarg
5
S. Bistarelli, and F. Santini. 2013. Coalitions of arguments: An approach with constraint programming. Fundam. Inform.
124(4):383–401.
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 17 / 17

37. Future Work
• Extend ConArg4 with the matrix approach.
• Test the real advantages of the reduction.
• Consider coalitions of arguments5.
4
http://www.dmi.unipg.it/conarg
5
S. Bistarelli, and F. Santini. 2013. Coalitions of arguments: An approach with constraint programming. Fundam. Inform.
124(4):383–401.
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 17 / 17

38. Future Work
• Extend ConArg4 with the matrix approach.
• Test the real advantages of the reduction.
• Consider coalitions of arguments5.
4
http://www.dmi.unipg.it/conarg
5
S. Bistarelli, and F. Santini. 2013. Coalitions of arguments: An approach with constraint programming. Fundam. Inform.
124(4):383–401.
Carlo Taticchi A Matrix Based Approach for Weighted Argumentation Frameworks 17 / 17

39. A Matrix Based Approach for
Weighted Argumentation Frameworks
Stefano Bistarelli1 Alessandra Tappini1 Carlo Taticchi2
stefano.bistarelli@unipg.it alessandra.tappini@unipg.it carlo.taticchi@gssi.it
Thanks for your attention!
Questions?
1Universit`a degli Studi di Perugia, Italy
2Gran Sasso Science Institute (GSSI), L’Aquila, Italy