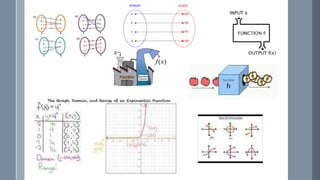
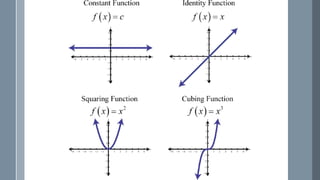
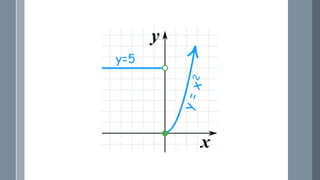
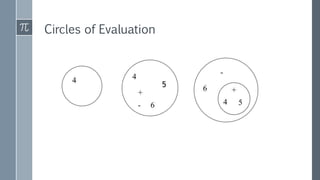
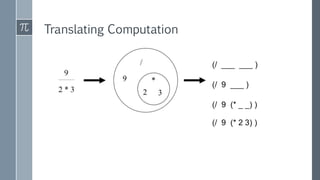
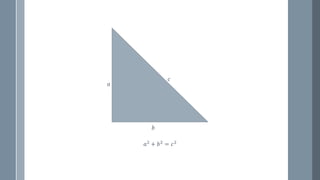
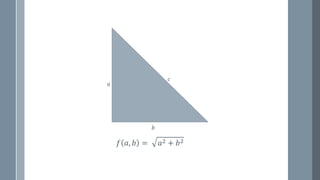
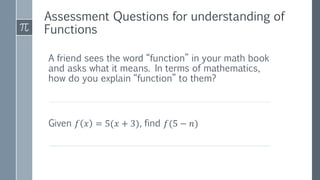
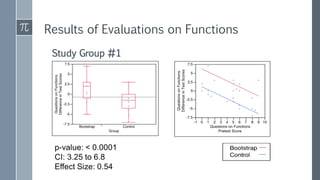
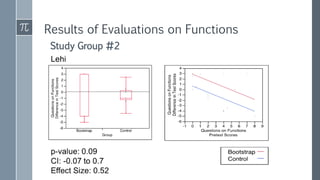
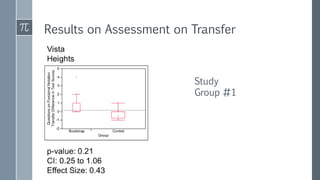
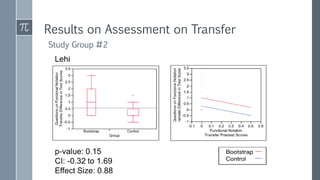
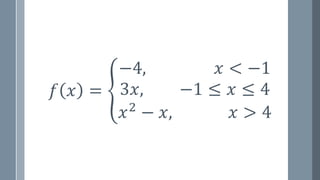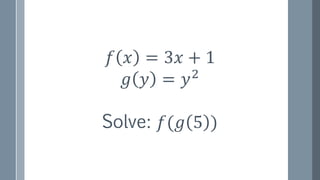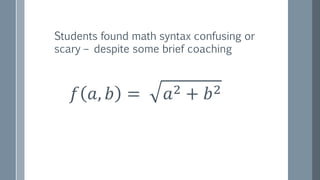The document discusses a curriculum using functional programming to teach algebra, piloted in the summer of 1967, highlighting how programming provides concrete insights into mathematical concepts like functions. It details the experiences of two Bootstrap courses taught at different schools, their assessment methods, and the students' struggles with mathematical syntax compared to programming syntax. The findings suggest that while programming can teach some mathematical principles, the transfer of knowledge from programming to traditional math understanding is limited.

1. Teaching Algebra Through
Functional Programming
Using Bootstrap Curriculum

2. Thanks to our Sponsors!
Partners
Premier
Logo:

3. Why Use
Programming to
Teach Math

9. With support from the US Office of
Naval Research, Logo was pilot-
tested in the summer of 1967 with
fifth- and sixth-grade math students.

10. The reason that a laboratory is not traditionally used in
mathematical study is not that it would be less valuable there
than in biology, chemistry, or physics; rather, the idea of a
mathematical experiment was, until recently, unrealizable, and
barely conceivable, except in very special or superficial senses.
How could a person set in motion a sequence of
mathematical events or a mathematical process, and then see
its effects unfold? Using a computer with an appropriate
programming language adds this extra dimension to mathe-
matical experience; the important contribution of the computer
is a new and powerful operational universe for mathematical
experiment
By W. Feurzeig, S. Papert, Mo Bloom, R. Grant, C. Solomon.
Taken from the Final Report on the first fifteen months of the LOGO Project,
November 30, 1969.
Submitted to the National Science Foundation on Contract NSF-C 558.
Copies will be available from ERIC

11. Programming can be used to give students very
specific insights into a number of key concepts.
Ideas such as variable and function remain, to say
the least, obscure for many high school students.
Indeed, college students often have trouble with the
many roles of the “x” in algebra: sometimes it
appears to be a number, sometimes a subtly
different kind of object called a variable, and on
other occasions it is to be treated as a function…
In programming, the distinctions arise concretely.
By W. Feurzeig, S. Papert, Mo Bloom, R. Grant, C. Solomon.
Taken from the Final Report on the first fifteen months of the LOGO Project,
November 30, 1969.
Submitted to the National Science Foundation on Contract NSF-C 558.
Copies will be available from ERIC

12. Logo Turtles

13. What is a function?

16. 𝑓 𝑥 =
−4, 𝑥 < −1
3𝑥, −1 ≤ 𝑥 ≤ 4
𝑥2
− 𝑥, 𝑥 > 4

18. 𝑓 𝑥 = 3𝑥 + 1
𝑔 𝑦 = 𝑦2
Solve: 𝑓(𝑔 5 )

19. Definition of a function
› a relationship or expression involving one or more
variables (dictionary.com)
› a mathematical correspondence that assigns exactly one
element of one set to each element of the same or
another set (merriam-webster.com)
› a process or a relation that associates each element x of
a set X, the domain of the function, to a single
element y of another set Y (wikipedia)

20. How do programmers
define a function?

21. Functions in programming
› method
› procedure
› subroutine
› statement
› abstraction
› encapsulation
› calculation
› grouping
› named section (Wikipedia)

23. Bootstrap applies mathematical
concepts and rigorous programming
principles to creating a simple
videogame

24. Students create a simple, 3-character game involving a
player, a target and a danger. They design what each
character looks like, and use algebraic concepts to detect
collisions.

25. Introduction to Scheme
› Prefix language with parenthesis
› (+ 1 2)
› (define (foo (a b)) (+ a b))
› (define (foo (a b c)) (+ a (- b c)))

26. WeScheme (a subset of Scheme)
› Students are given
predefined functions for
– IO
– higher-order functions
› Are able to focus on
calculations

27. Circles of Evaluation

28. Translating Computation

31. 𝑎2
+ 𝑏2
= 𝑐2
𝑎
𝑏
𝑐

32. 𝑎
𝑏
𝑐
𝑓 𝑎, 𝑏 = 𝑎2 + 𝑏2

33. double distance(int x, int y, int x1, int y1) {
double aSquared = Math.pow(x - x1, 2);
double bSquared = Math.pow(y - y1, 2);
double cSquared = aSquared + bSquared;
return Math.sqrtc(cSquared);
}
Why Scheme? Why not Java?
A first course in computer programming should not be about the current “hot”
language in industry – which may be obsolete by the time today’s freshmen
graduate – but rather about lasting, transferable concepts and practices of good
programming. Yet beginning programming students spend much of their time
wrestling with the language, and often mistake that as the subject of the course; the
programming language distracts from the course material. – Stephen Bloch
(Math/CS Department Adelphi University)

34. Why Scheme?
› Syntax is simple
– Parenthesis
– Operators
– define keyword
› Functional
– Not imperative

35. Study on Bootstrap Curriculum
› The Bootstrap curriculum was taught at two schools
› An assessment on math skills was given before and after
the course to both the study and control groups
› Assessments were statistically analyzed
› Interviews were conducted with all the participants in the
Bootstrap course

36. Bootstrap course #1
› Taught at a middle school as an after school class
› Participants volunteered
– 14 started the course, 9 finished
› The course lasted about 6 weeks
– Twice a week
– 1 ½ hours each class
› Control group was a CTE (Careers, Technology,
Engineering) class

37. Bootstrap course #2
› Taught at a high school during school
› Participants where chosen by administration
– juniors and seniors who could not pass basic algebra
– students received ½ math credit for participation in math
– 14 started the course, 9 finished
› The course lasted about 6 weeks
– Twice a week
– 1 ½ hours each class
› Control group was a CTE (Careers, Technology,
Engineering) class

38. A friend sees the word “function” in your math book
and asks what it means. In terms of mathematics,
how do you explain “function” to them?
Given 𝑓 𝑥 = 5(𝑥 + 3), find 𝑓(5 − 𝑛)
Assessment Questions for understanding of
Functions

39. Assessment Questions for understanding of
Functions

40. Results of Evaluations on Functions
Study Group #1

41. Results of Evaluations on Functions
Study Group #2

42. Transfer from Scheme to Algebra
(define distance (x y x1 y1)
(sqrt
(+ (sq (-(x x1) sq(- (b b1)))))
𝑓 𝑥, 𝑥1
, 𝑦, 𝑦1
= (𝑥1 − 𝑥)2+(𝑦1 − 𝑦)2

43. Consider the following function:
On a graph, plot and label and .
How far apart are the two points?
Show your work.
f (x) = 3
4 x + 2
f (0) f (4)
Using the following two functions,
find the value of the composite function, f (g(5)).
Show your work.
f (x) = 2x
g(y) = y2
Questions on Transferring Programming
Functions to Algebra Functions

44. Questions on Transferring Programming
Functions to Algebra Functions

45. Results on Assessment on Transfer
Study
Group #1

46. Results on Assessment on Transfer
Study Group #2

47. Observations
› Students in both study and control groups didn’t answer
the harder questions
› In interviews with the study group
– when asked why they didn’t answer the hard questions
– did not remember what the syntax meant
– said the algebra syntax looked scary
– students very comfortable with the Scheme syntax

48. 𝑓 𝑎, 𝑏 = 𝑎2 + 𝑏2
Students found math syntax confusing or
scary – despite some brief coaching

49. (define distance (a b)
(sqrt
(+ (sq a) sq(b))))
Students showed in interview they were comfortable with
Scheme Syntax, probably because they had worked with it
in building their games.

51. Conclusions
› Programming in most languages can teach some math
principles
– PEMDAS
– Cartesian Planes
– Formulas like Pythagorean Theorem
› Programming does not transfer well to math
symbols/syntax
– Unfamiliarity
– The term scary is used
› Programming can teach Computational Thinking

52. Conclusions
› Functional Programming is very good at teaching
functions
› The understanding of functions gained may help with the
concept in later education

53. The demonstration of positive transfer from
programming into algebra is exciting, but the
findings should not be generalized to suggest that
merely “learning to program” would result in
mathematical gains for students. Bootstrap’s
success rests on a conscious selection of
programming language, software tools, curriculum
and pedagogical practice that are drawn from
the algebraic domain.
-Emanuel Schanzer in his Doctoral Thesis

54. Robert W. Lee
https://www.linkedin.com/in/roblee
https://twitter.com/leerobertw
http://robertwlee.weebly.com
Master’s Thesis
https://scholarsarchive.byu.edu/etd/3519
Bootstrap website
http://www.bootstrapworld.org/
Schanzuer at TedX
https://www.youtube.com/watch?v=FbqnaoU-3VI
Bootstrap on Code.org
https://studio.code.org/s/algebra
Schanzer Doctoral Thesis
https://dash.harvard.edu/handle/1/16461037
Educator Resources
https://code.org/educate/curriculum/3rd-party