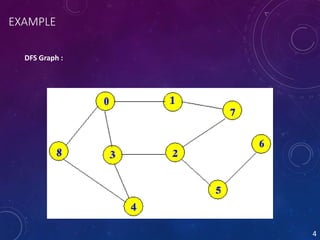
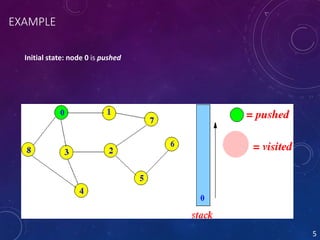
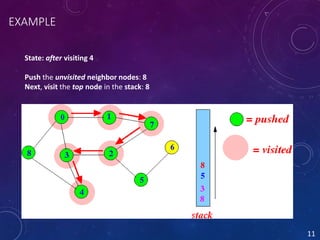
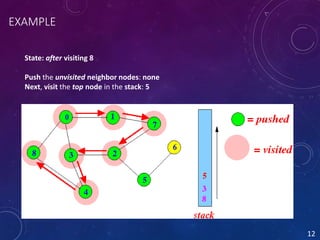
Depth-first search (DFS) is an algorithm for traversing tree and graph data structures. It starts at the root node and explores as far as possible along each branch before backtracking. It continues visiting neighbors in a recursive pattern, recursively visiting all unvisited neighbors of each visited vertex before backtracking. The DFS algorithm works by starting with any vertex on a stack, visiting and removing it from the stack while adding its unvisited neighbors to the top of the stack, repeating until the stack is empty.

1. DEPTH-FIRST SEARCH
ALGORITHM
T.M.D.M DISSANAYAKE
SEU / IS /15 /ICT / 045
FACULTY OF TECHNOLOGY

2. DFSALGORITHM
• Depth-first search (DFS) is an algorithm for traversing or searching tree or
graph data structures. The algorithm starts at the root node and explores
as far as possible along each branch before backtracking.
• DFS will continue to visit neighbors in a recursive pattern
• Whenever we visit v from u, we recursively visit all unvisited neighbors of v.
• Then we backtrack (return) to u. u
v
w1 w2
w3
2

3. CONTINUE… DFS ALGORITHM
The purpose of the algorithm is to mark each vertex as visited while
avoiding cycles.
The DFS algorithm works as follows:
• Start by putting any one of the graph's vertices on top of a stack.
• Take the top item of the stack and add it to the visited list.
• Create a list of that vertex's adjacent nodes. Add the ones which aren't
in the visited list to the top of stack.
• Keep repeating steps 2 and 3 until the stack is empty.
3

4. EXAMPLE
DFS Graph :
4

5. EXAMPLE
Initial state: node 0 is pushed
5

6. EXAMPLE
State: after visiting 0
Push the unvisited neighbor nodes: 8, 3, 1
Next, visit the top node in the stack: 1
6

7. EXAMPLE
State: after visiting 1
Push the unvisited neighbor nodes: 7
Next, visit the top node in the stack: 7
7

8. EXAMPLE
State: after visiting 7
Push the unvisited neighbor nodes: 2
Next, visit the top node in the stack: 2
8

9. EXAMPLE
State: after visiting 2
Push the unvisited neighbor nodes: 5, 3
Next, visit the top node in the stack: 3
9

10. EXAMPLE
State: after visiting 3
Node 0, already visited.
Push the unvisited neighbor nodes: 4
Next, visit the top node in the stack: 4
10

11. EXAMPLE
State: after visiting 4
Push the unvisited neighbor nodes: 8
Next, visit the top node in the stack: 8
11

12. EXAMPLE
State: after visiting 8
Push the unvisited neighbor nodes: none
Next, visit the top node in the stack: 5
12

13. EXAMPLE
State: after visiting 5
Push the unvisited neighbor nodes: 6
Next, visit the top node in the stack: 6
13

14. EXAMPLE
State: after visiting 6
Push the unvisited neighbor nodes: none
Next, visit the top node in the stack: 3
3 is visited: skip
14

15. EXAMPLE
Next, visit the top node in the stack: 8
8 is visited: skip
15

16. EXAMPLE
Result:
DONE
• The stack has become empty
• and all the nodes of the graph have been traversed.
16

17. EXAMPLE
Result:
The printing sequence of the graph will be :
0  1  7  2  3  4  8  5  6
Final Path
• All nodes are covered by DFS Algorithm
17

18. THANK YOU