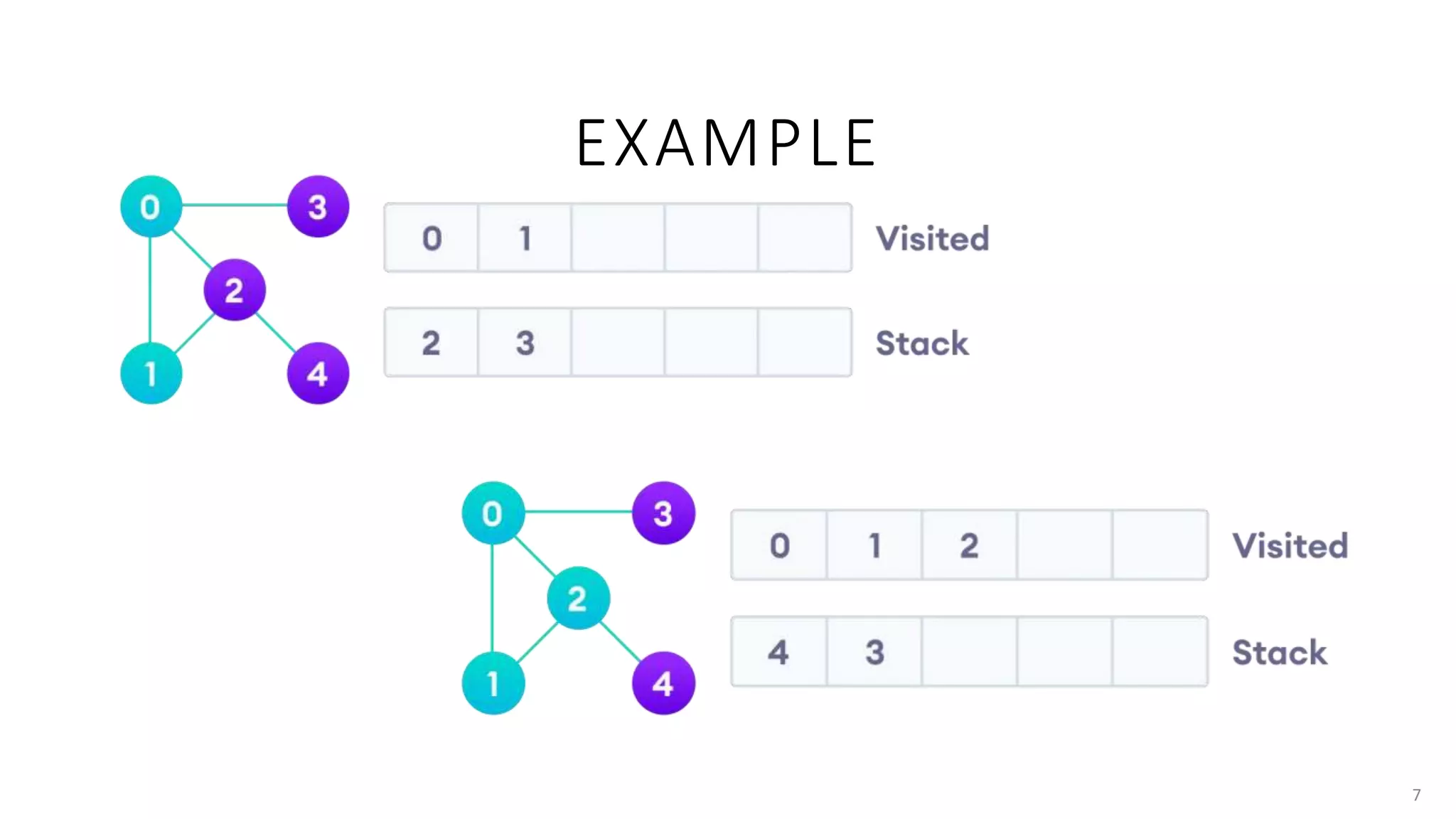
The document discusses depth first search (DFS), an algorithm for traversing or searching trees or graphs. It begins with an introduction to DFS, explaining that it explores edges out of the most recently discovered vertex as deep as possible before backtracking. It then provides pseudocode for the DFS algorithm and explains that it has a time complexity of O(V+E), where V is the number of vertices and E is the number of edges. Finally, it lists some applications of DFS such as cycle detection, solving mazes, and analyzing networks.

1. DEPTH FIRST SEARCH
ALEEZA SHAKEEL 2021-CS-15
LAIBA 2021-CS-51

2. TOPICS:
I N T R O D U C T I O N
D e p t h f i rs t s e a rc h A l g o r i t h m
E xa m p l e
T i m e c o m p l e x i t y
Ps e u d o c o d e
A p p l i c a t i o n s o f D F S
2

3. 3
INTRODUCTION
The strategy followed by depth-first search is, as its
name implies, to search “deeper” in the graph
whenever possible. Depth-first search explores
edges out of the most recently discovered vertex
that still has unexplored edges leaving it. Once all
of ’s edges have been explored, the search
“backtracks” to explore edges leaving the vertex
from which was discovered.
This process continues until we have discovered all
the vertices that are reachable from the original
source vertex. If any undiscovered vertices remain,
then depth-first search selects one of them as a
new source, and it repeats the search from that
source. The algorithm repeats this entire process
until it has discovered every vertex
3

4. 4
4
• A standard DFS implementation puts each vertex of the graph
into one of two categories:
1. Visited
2. Explored
• The purpose of the algorithm is to mark each vertex as visited
while avoiding cycles.
• The DFS algorithm works as follows:
1. Start by putting any one of the graph's vertices on top of a
stack.
2. Take the top item of the stack and add it to the visited list.
3. Create a list of that vertex's adjacent nodes. Add the ones
which aren't in the visited list to the top of the stack.
4. Keep repeating steps 2 and 3 until the stack is empty.
DEPTH FIRST SEARCH ALGORITHM

5. EXAMPLE
D F S
5

6. EXAMPLE
6

7. EXAMPLE
7

8. EXAMPLE
8

9. PSEUDO CODE
9

10. TIME COMPLEXITY
10
Depth-first search visits every vertex once and checks every edge in the
graph once.
DFS complexity is:
O(V + E)
V=vertex
E=edges
O(V+E) assumes that the graph is represented as an adjancey list

11. Application of depth First Search Algorithm
11
• Depth-first search is used in scheduling problems, cycle
detection in graphs, and solving puzzles with only one solution,
such as a maze or a sudoku puzzle.
• Analyzing networks, like testing if a graph is bipartite .
• Depth-first search is often used as a subroutine in network flow
algorithms
• DFS is also used as a subroutine in matching algorithms
in graph theory
• Depth-first searches are used in mapping routes
• scheduling, and finding spanning trees