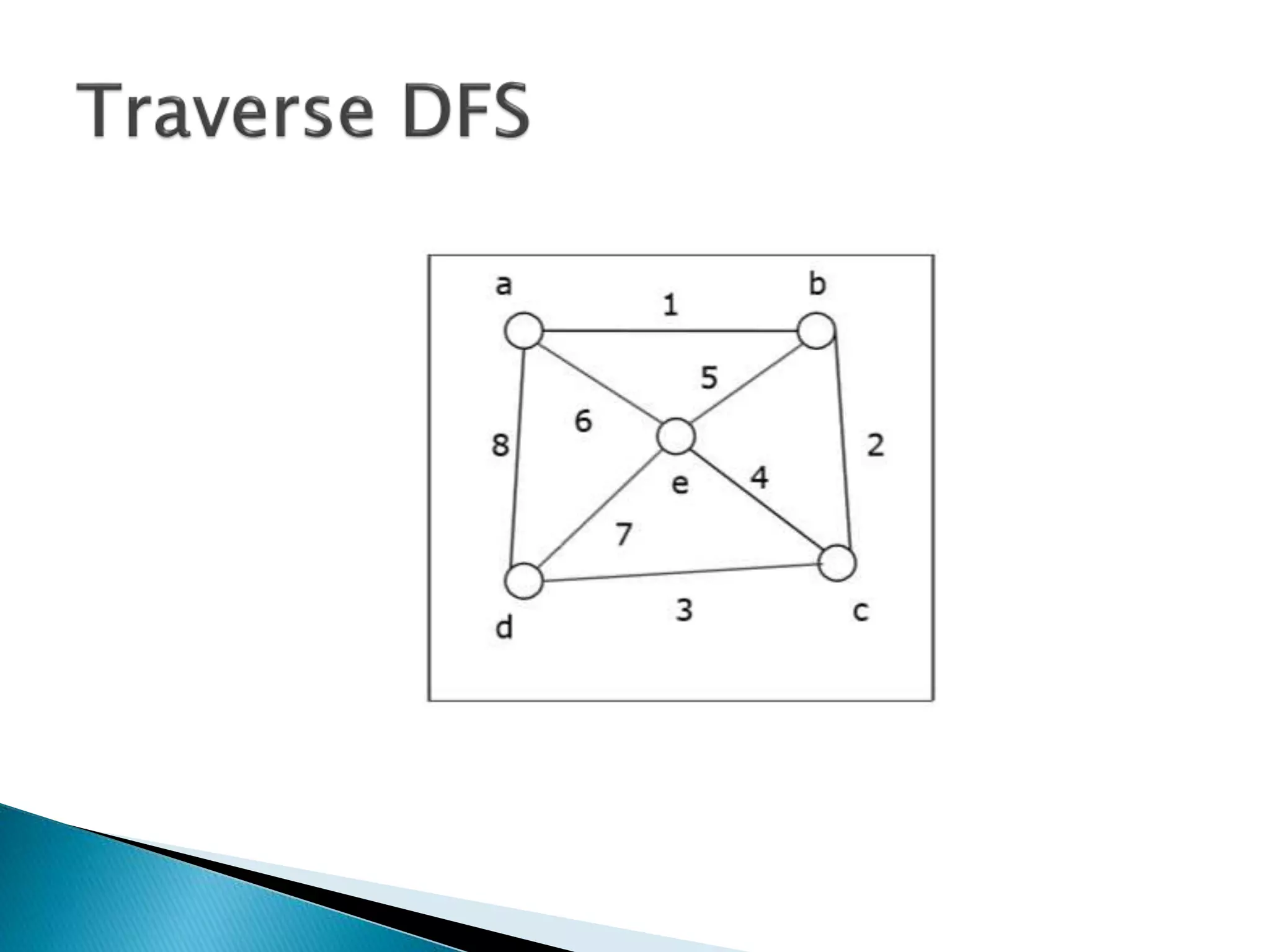
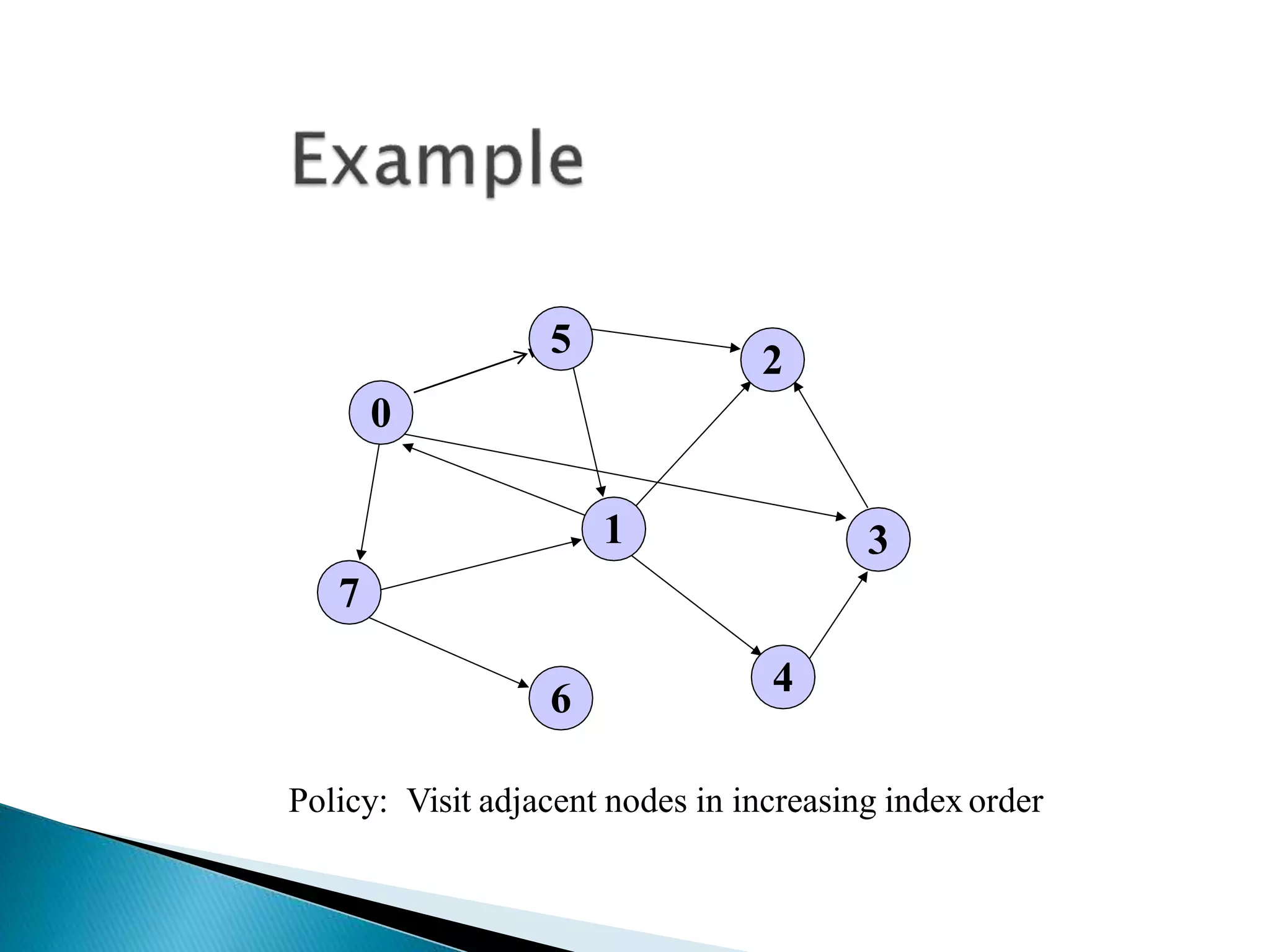
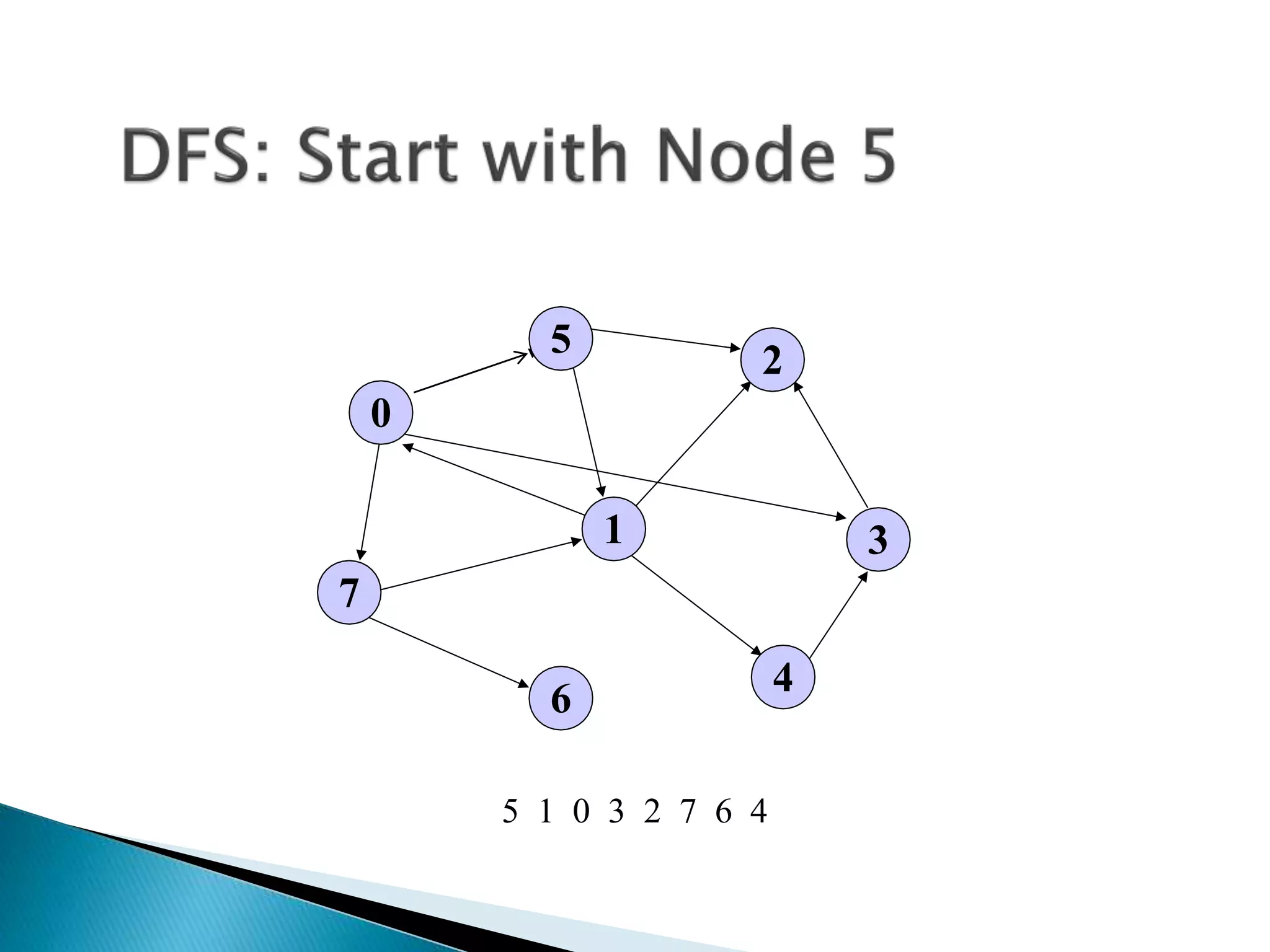
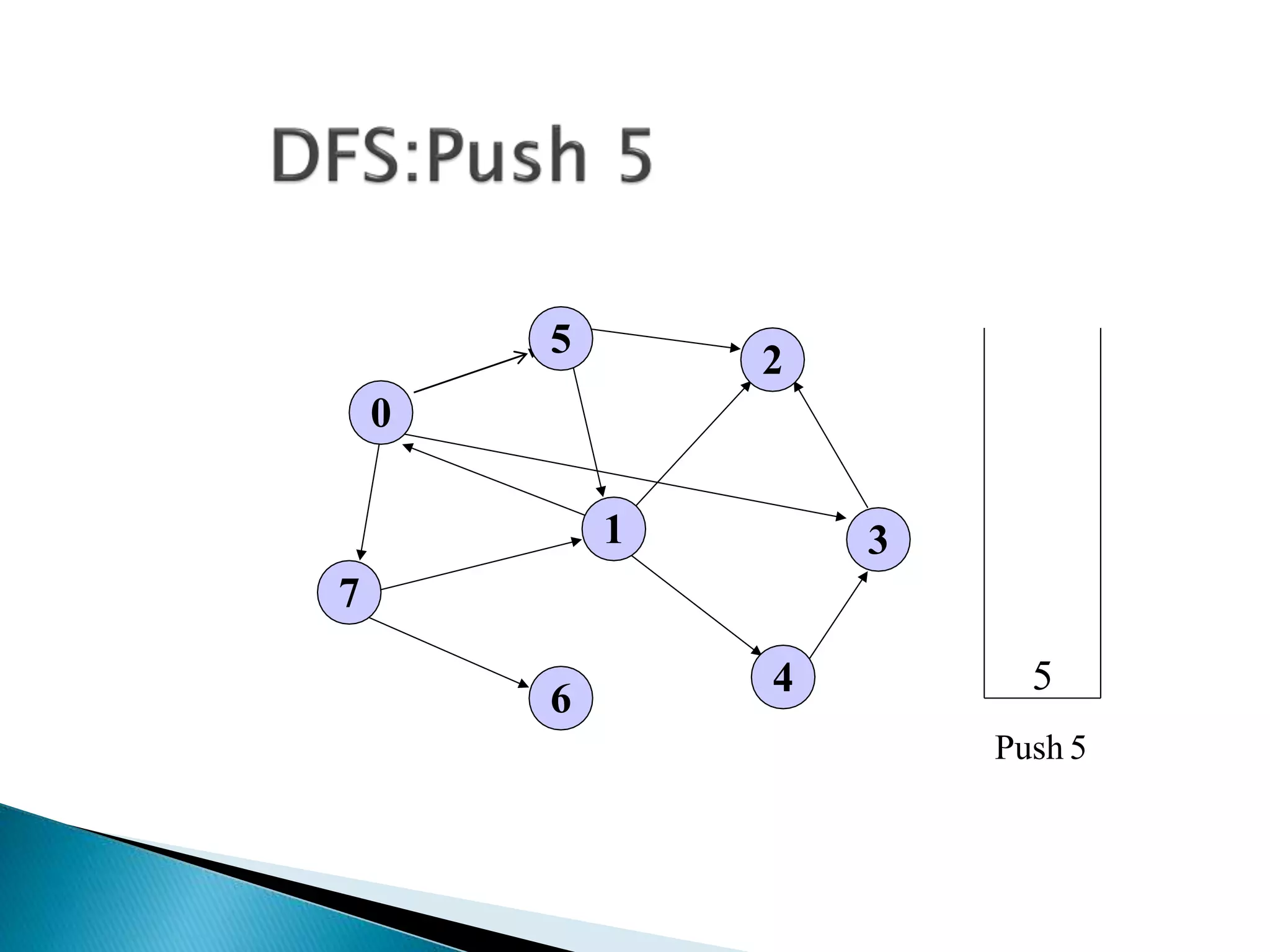
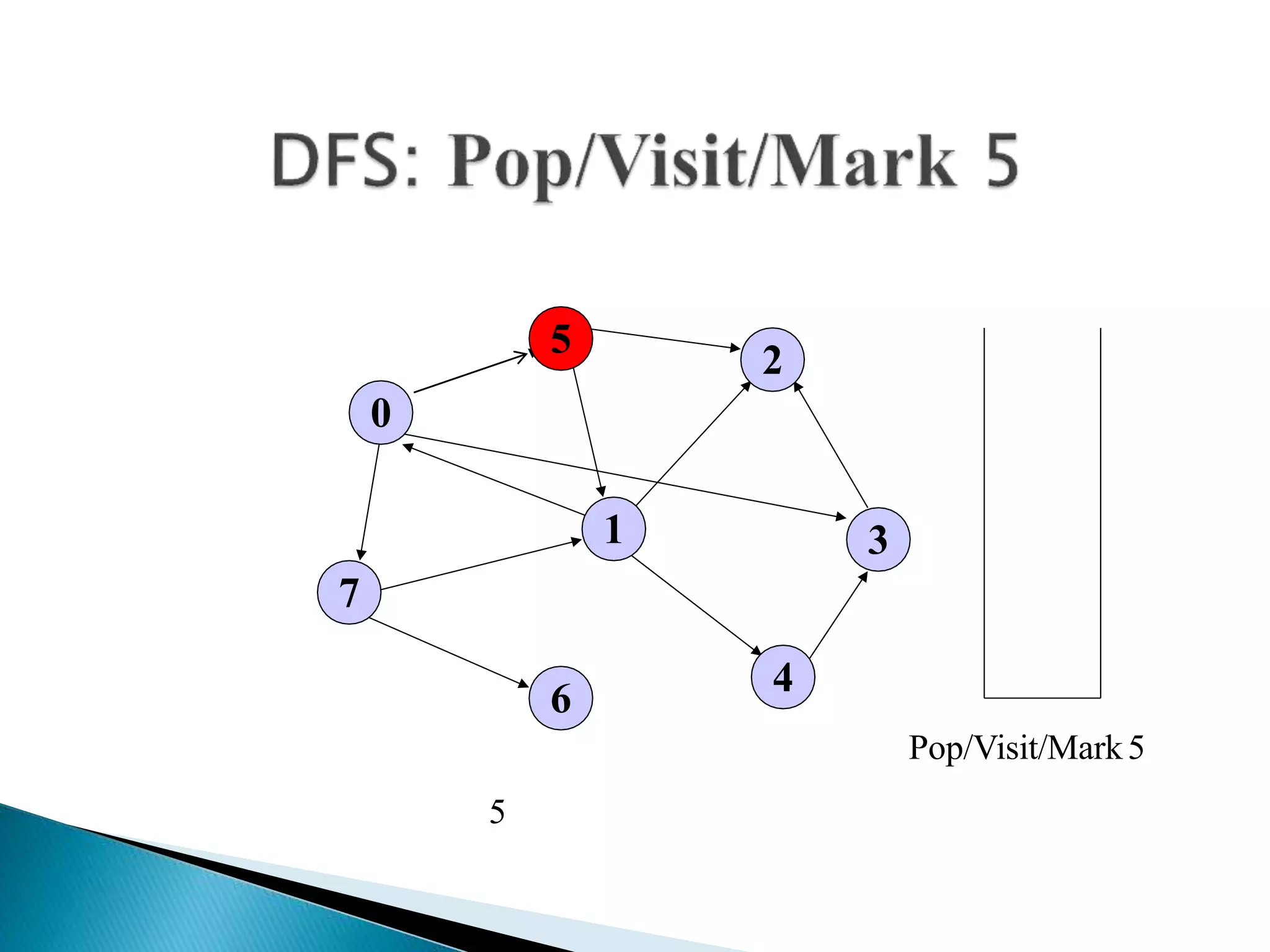
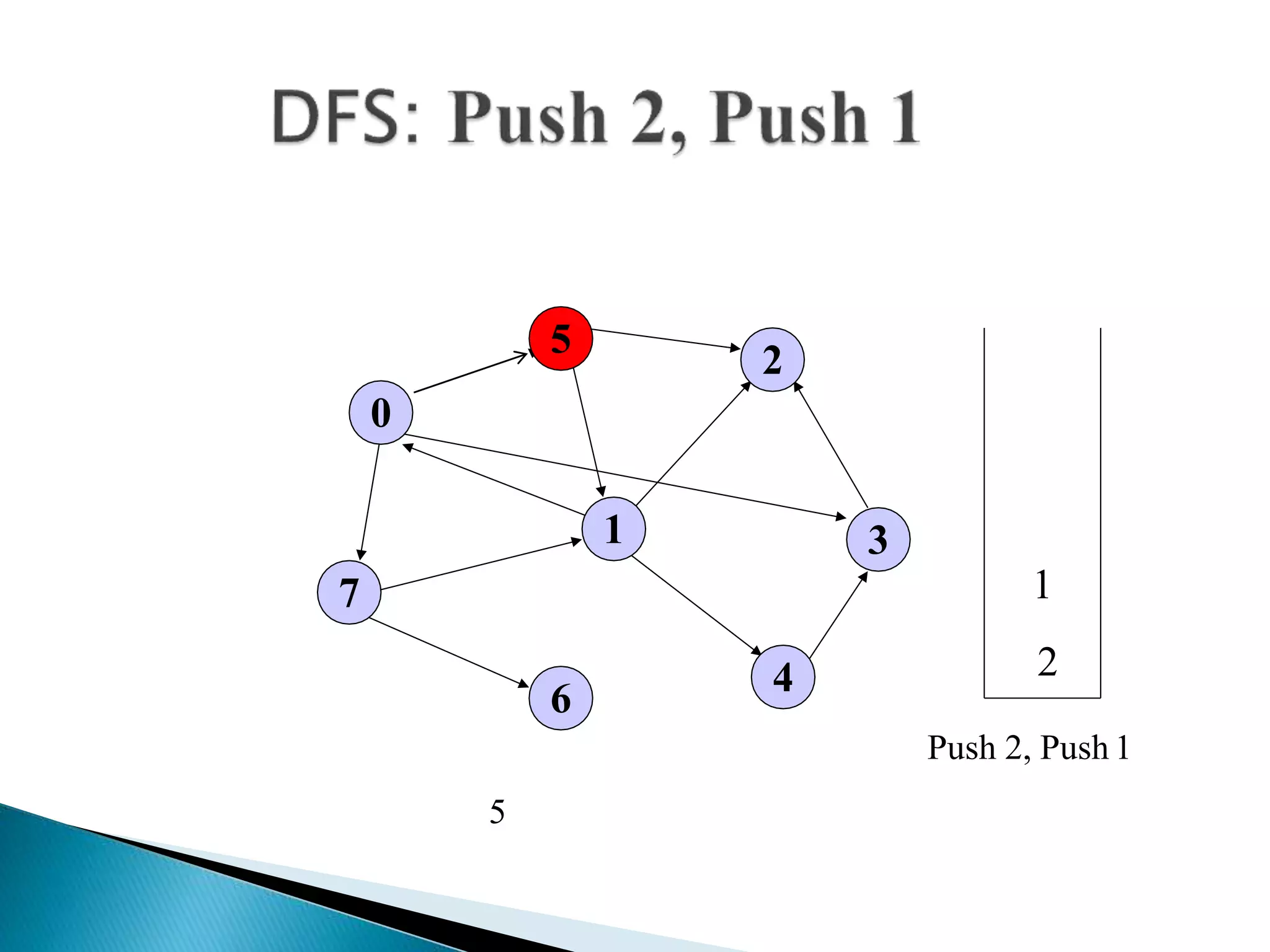
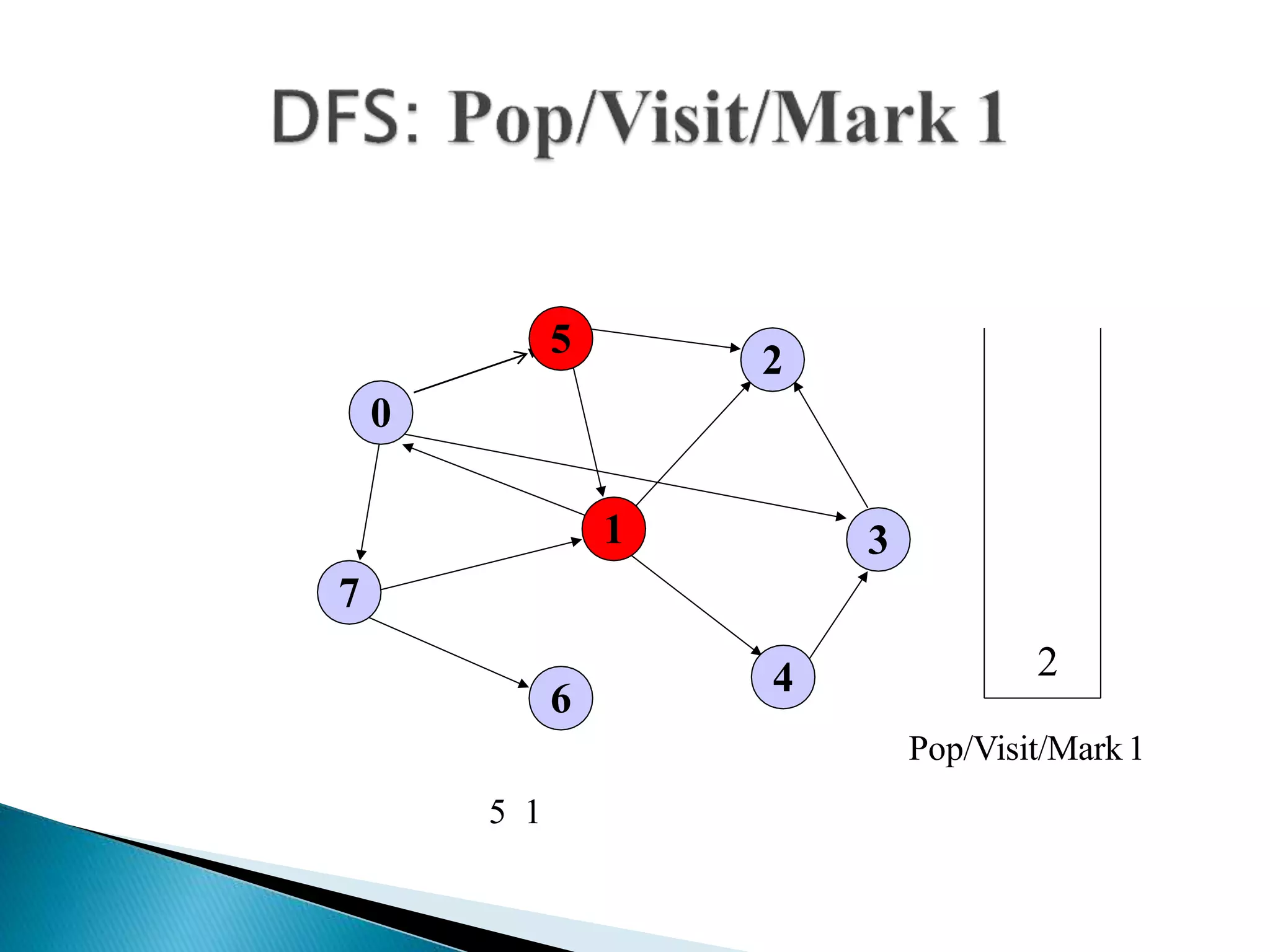
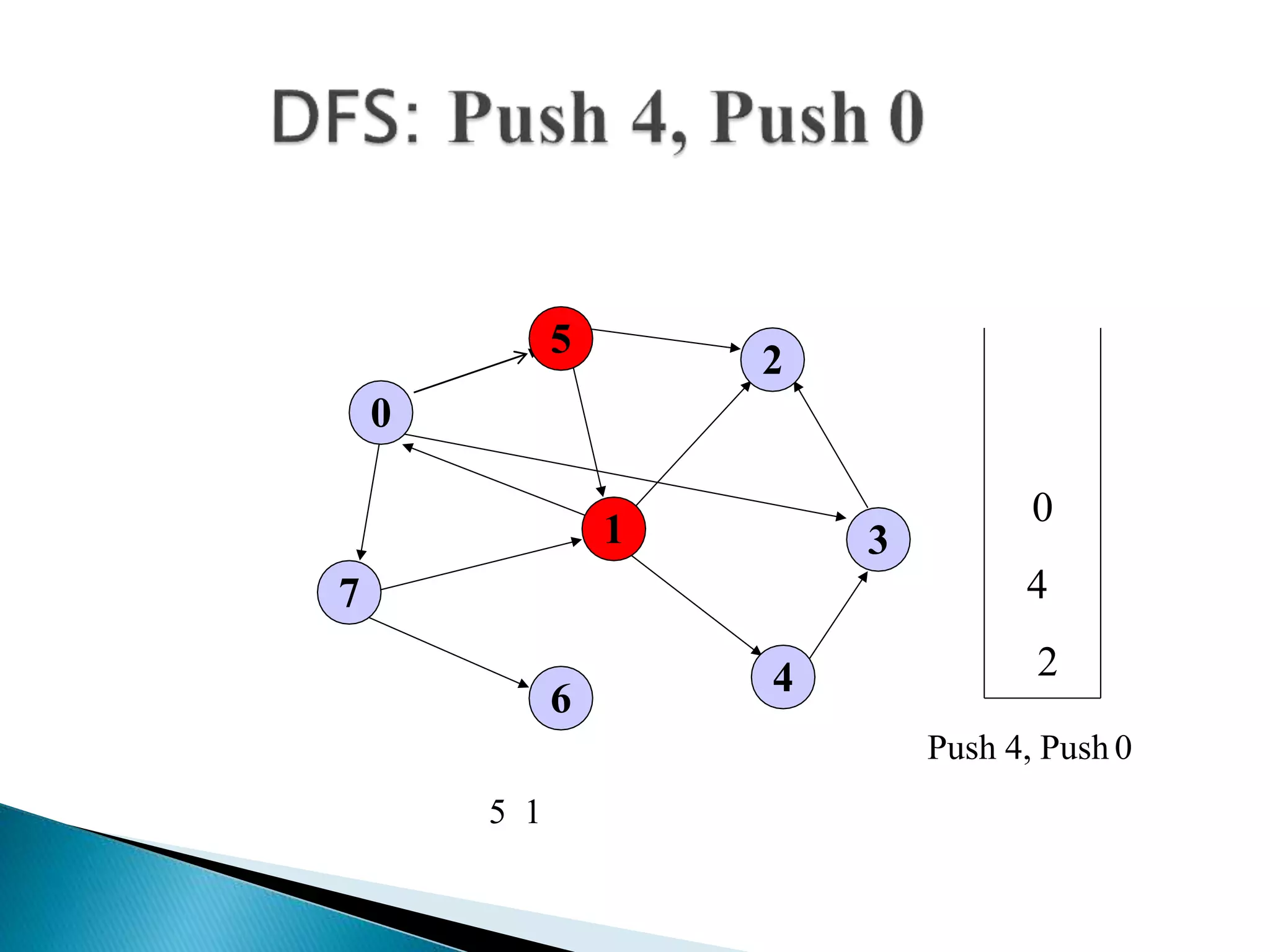
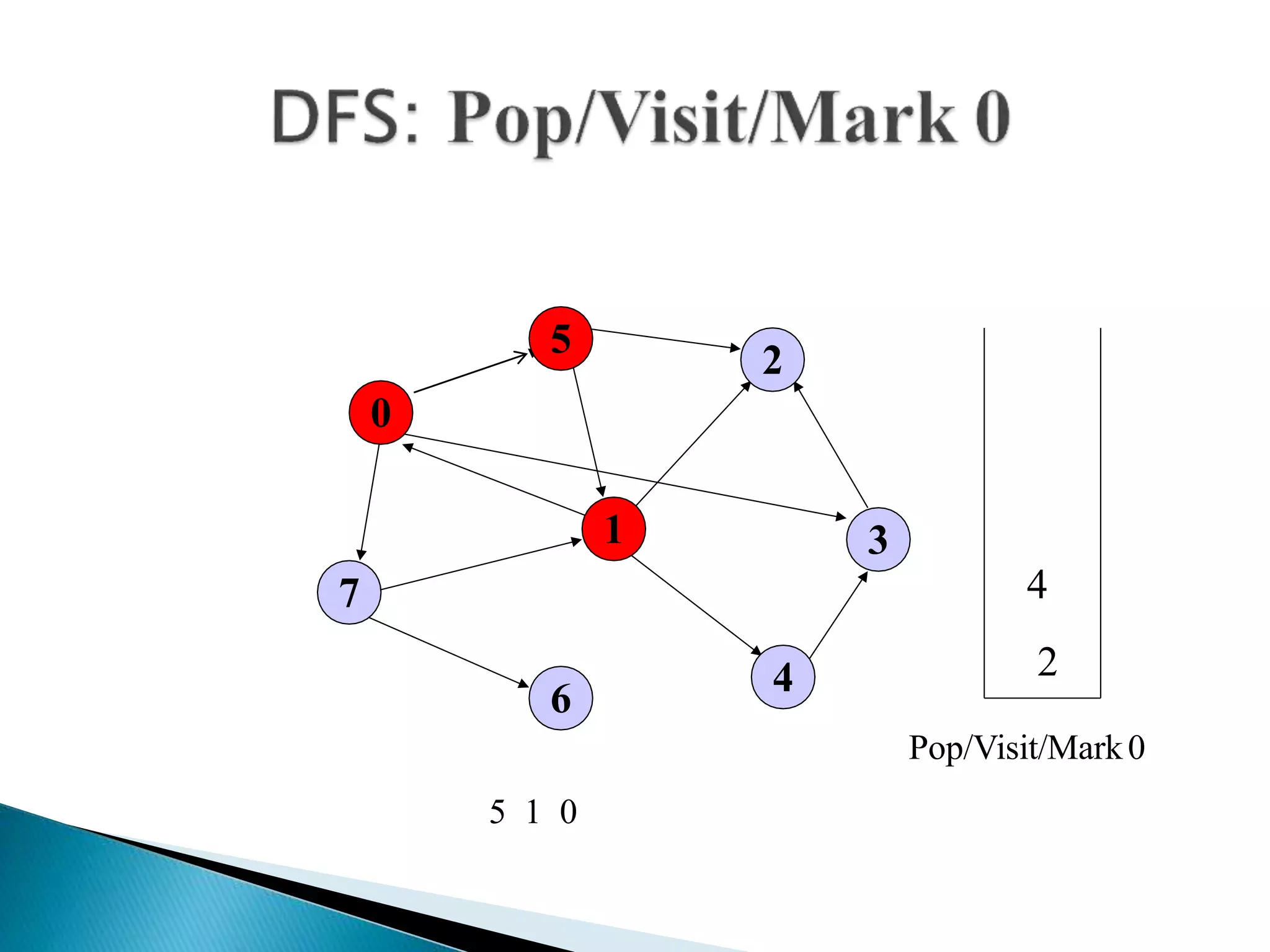
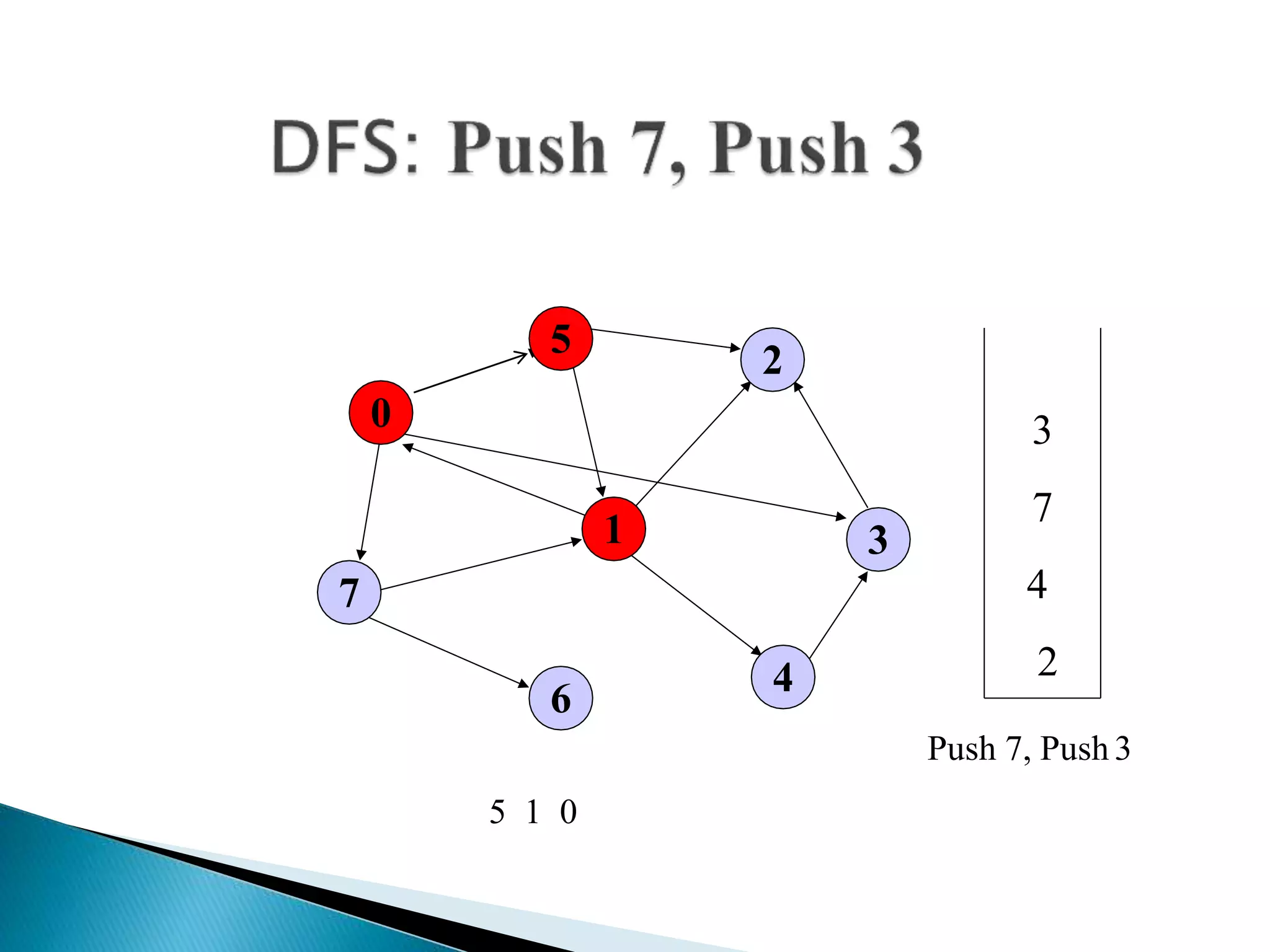
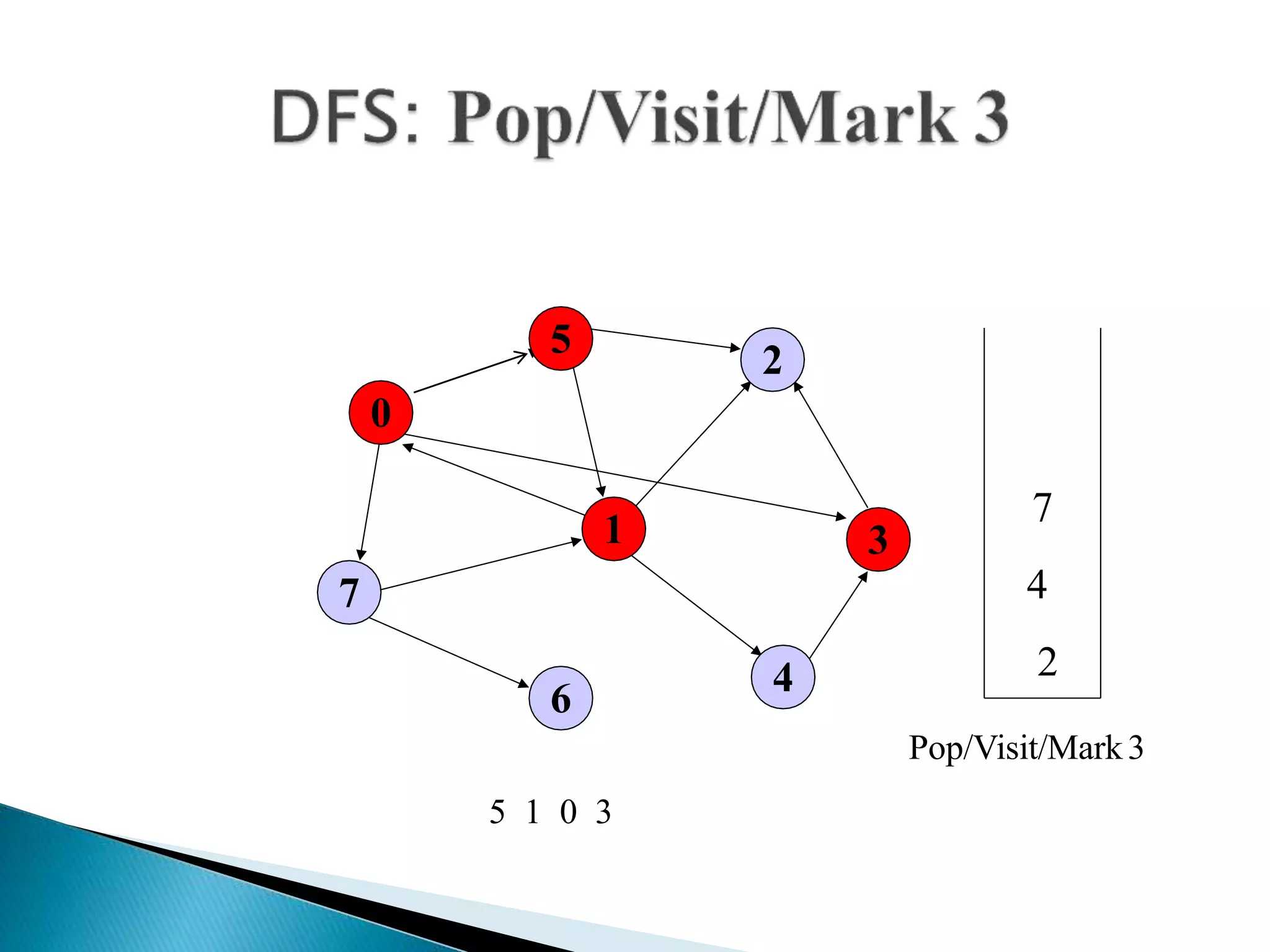
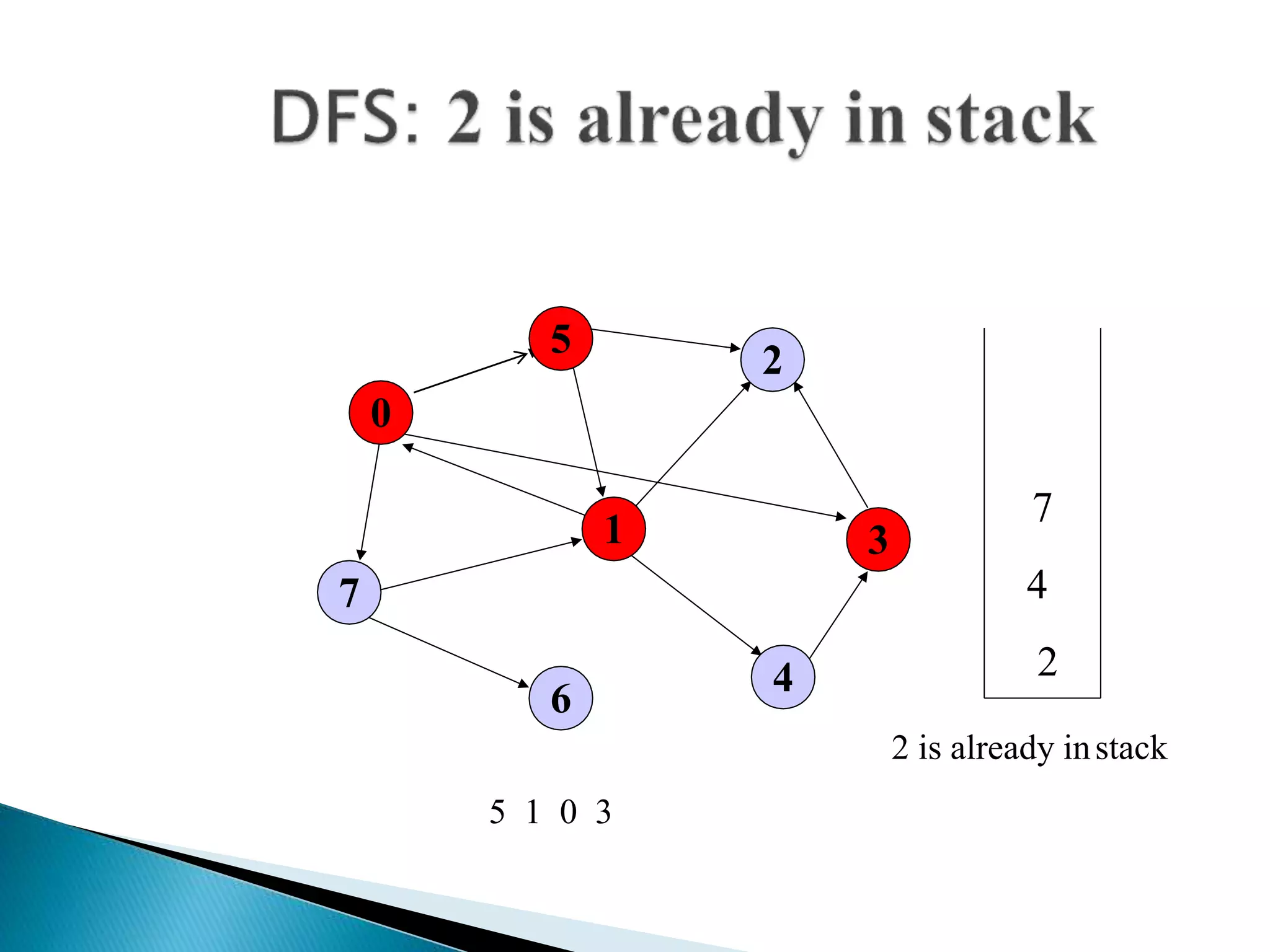
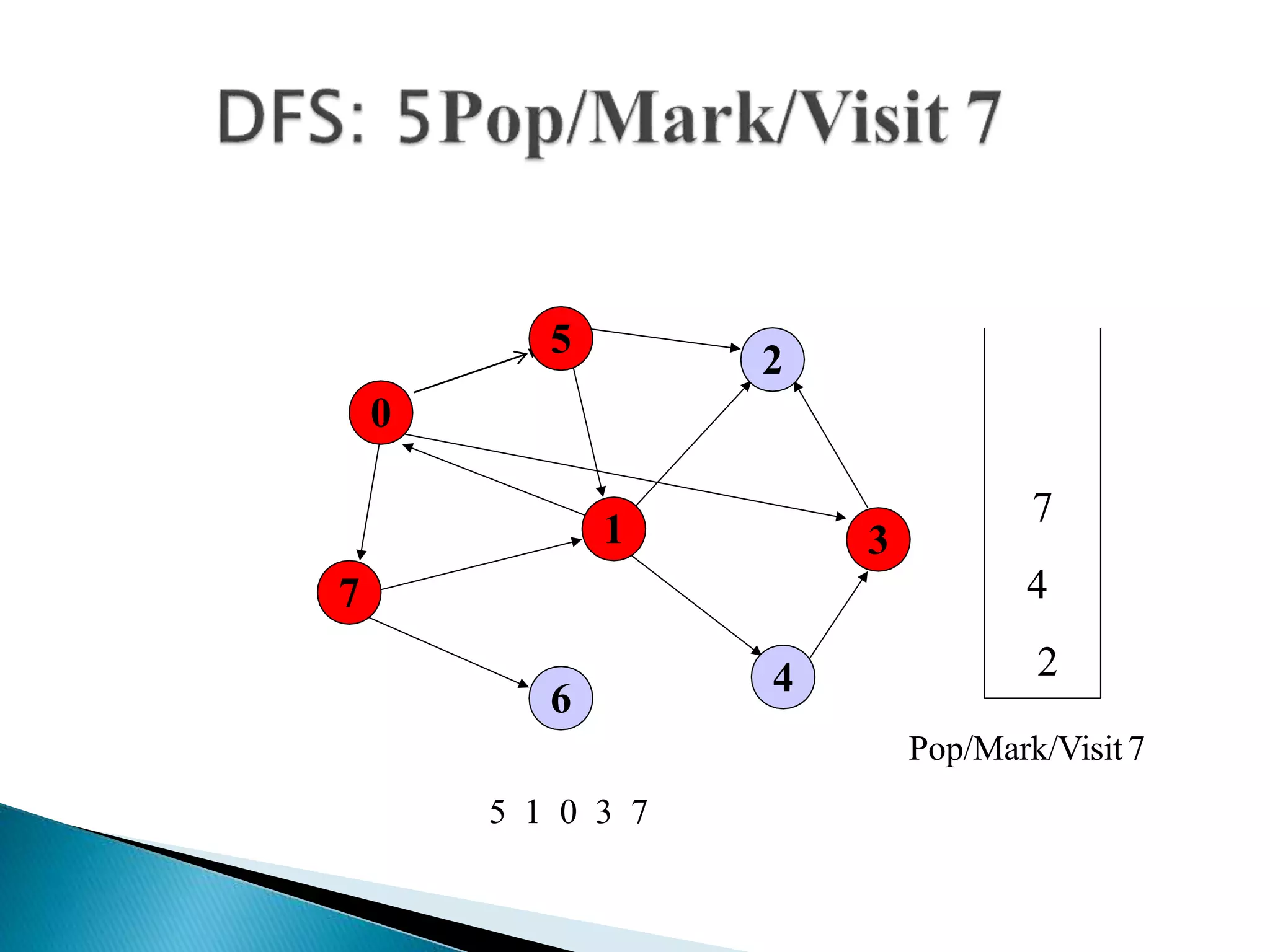
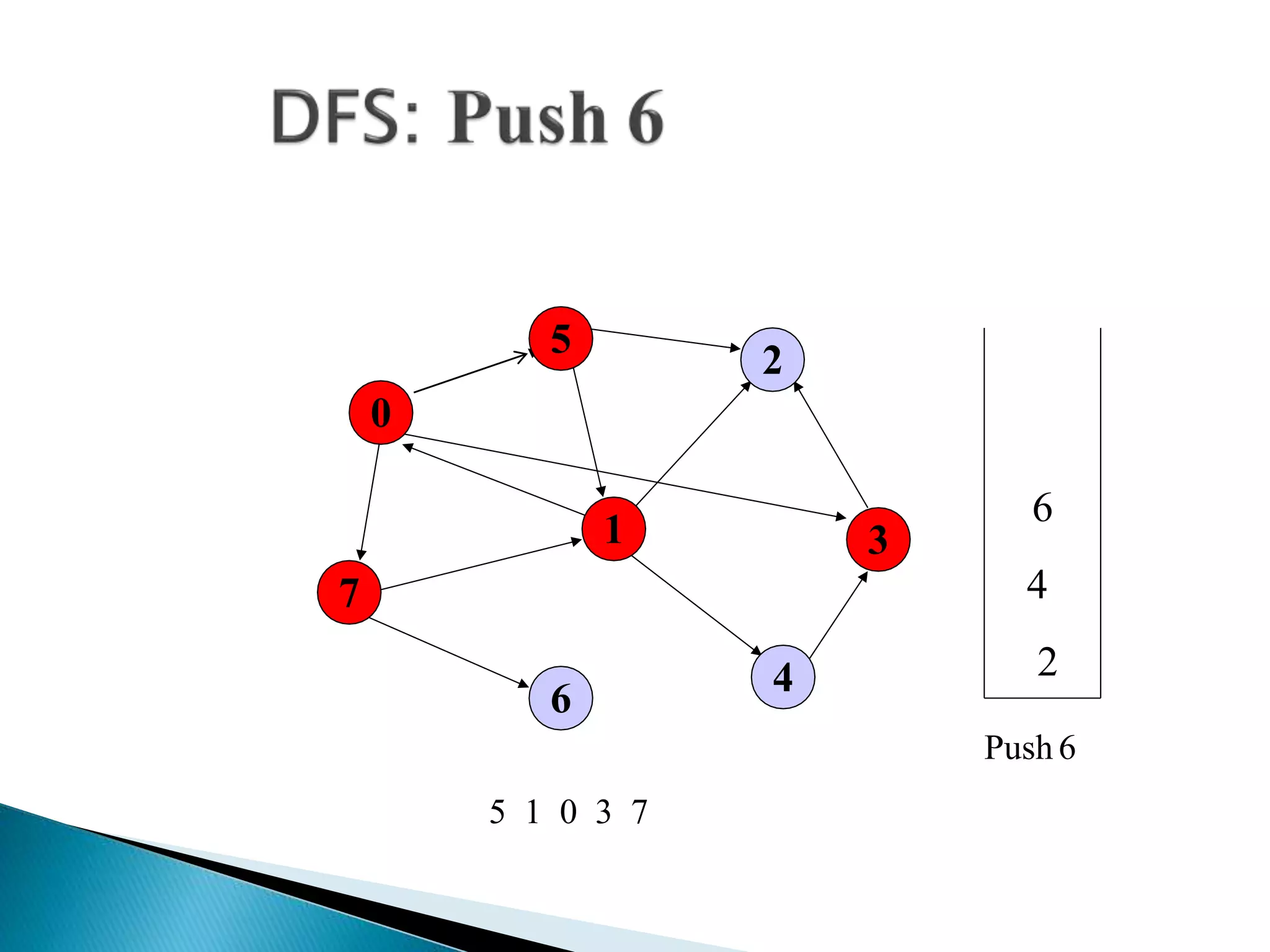
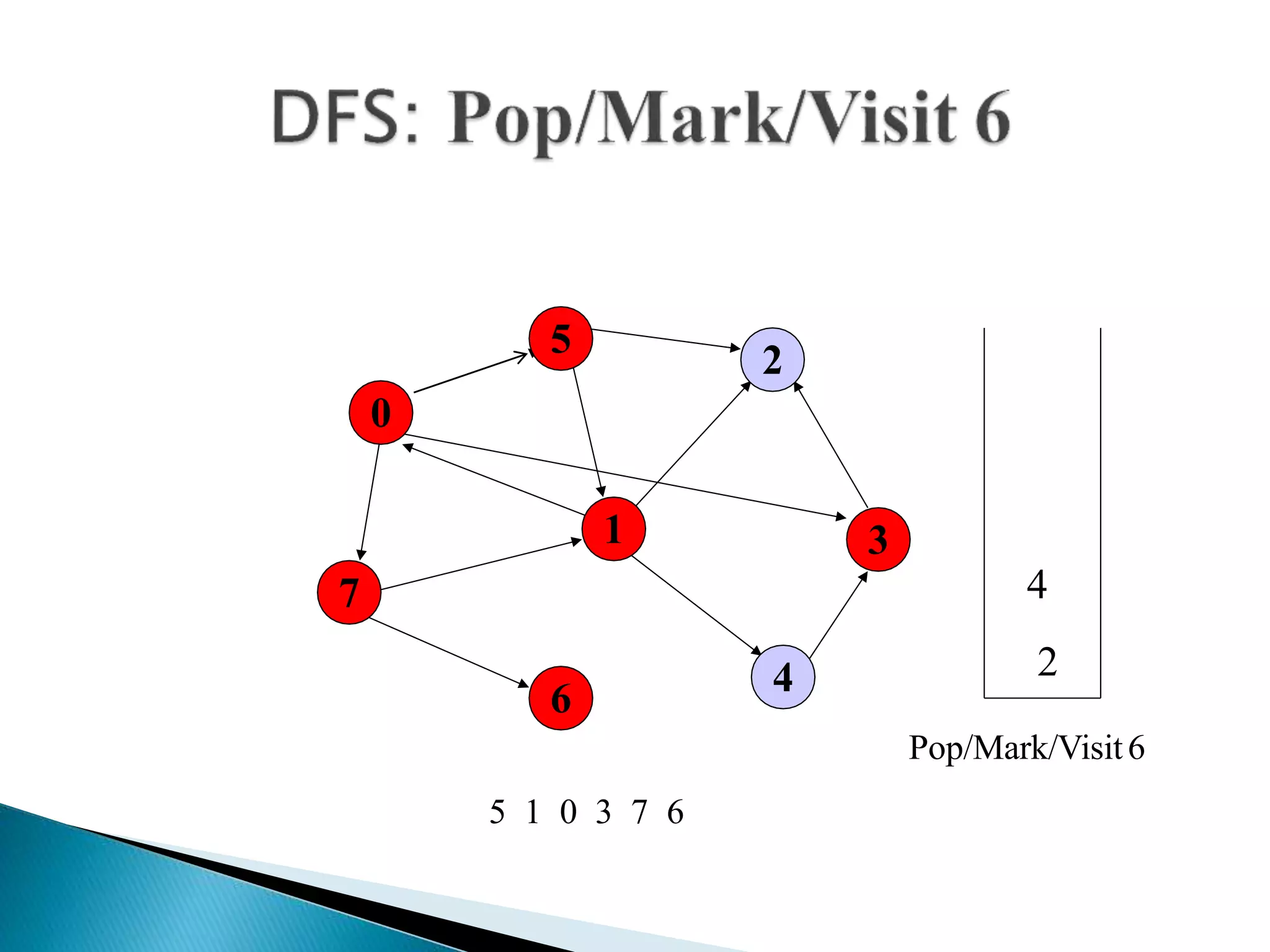
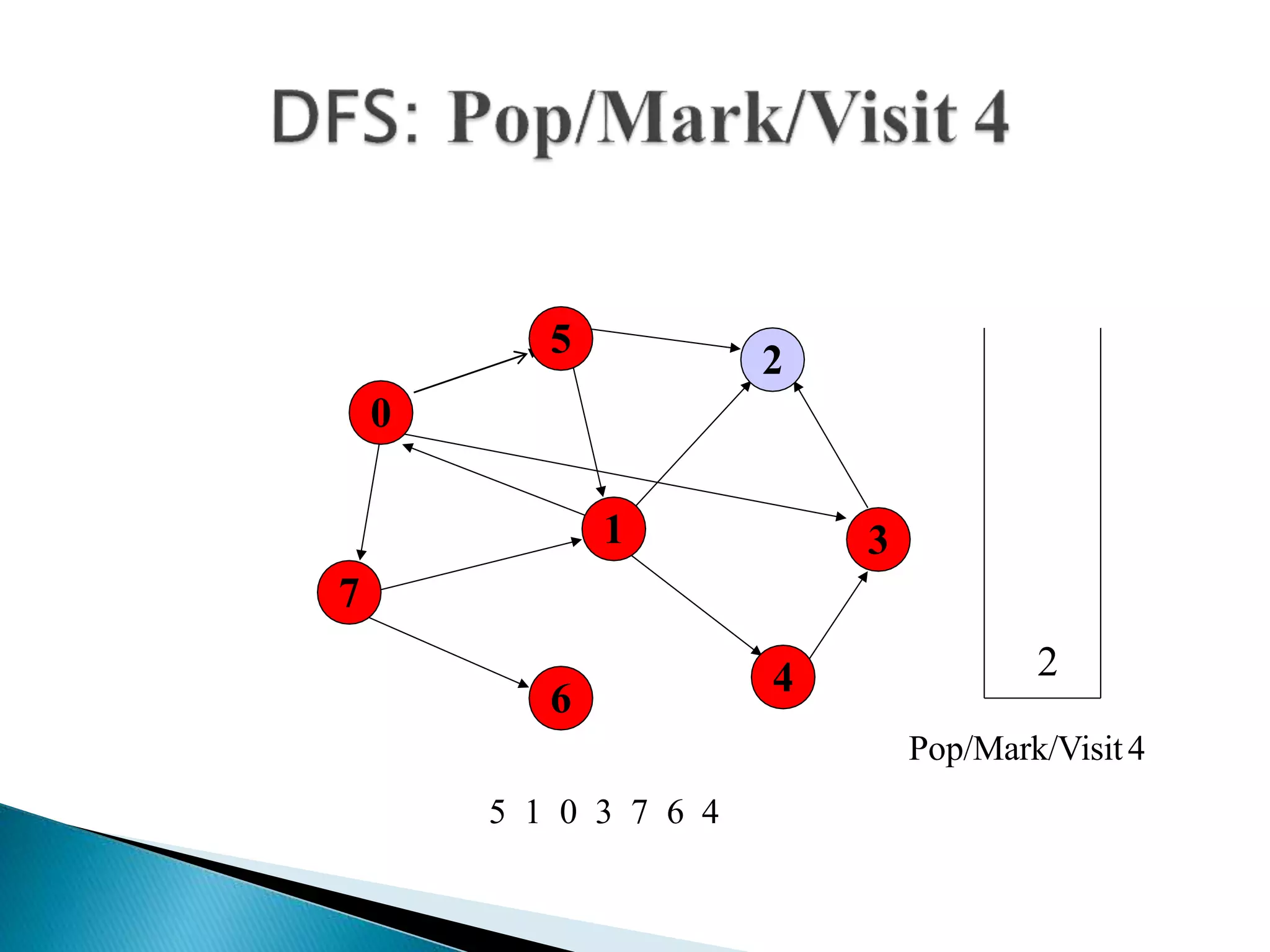
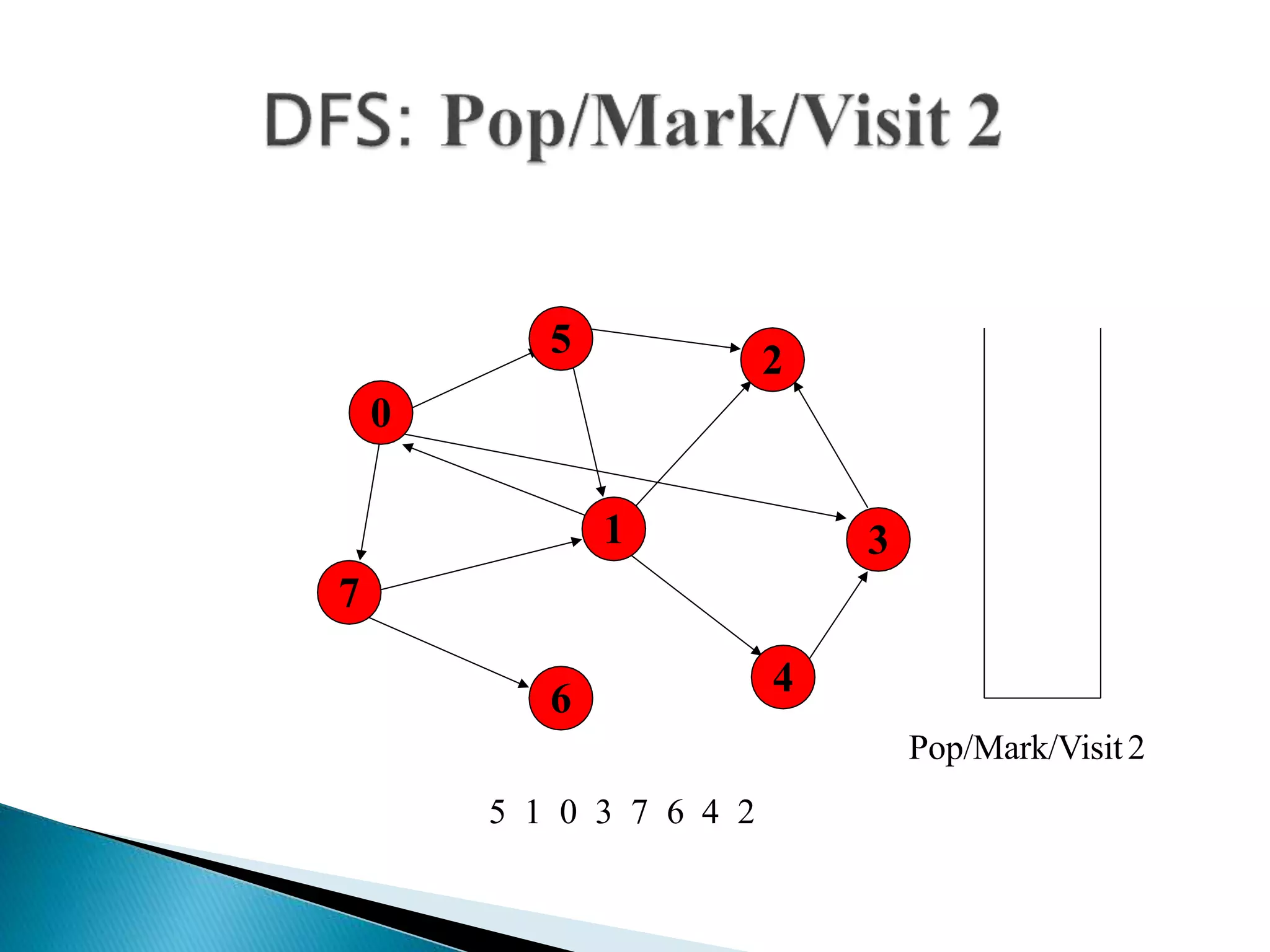
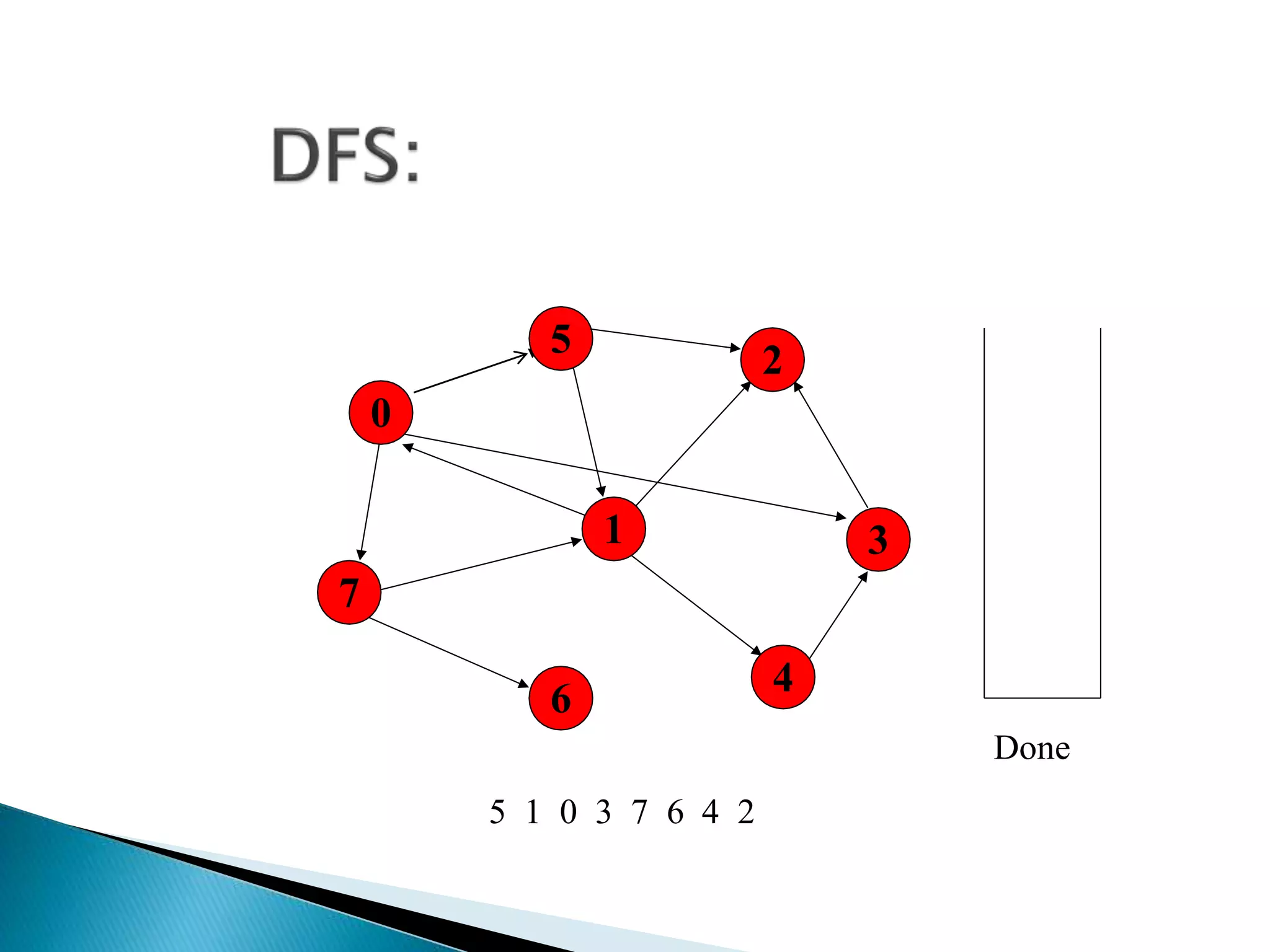
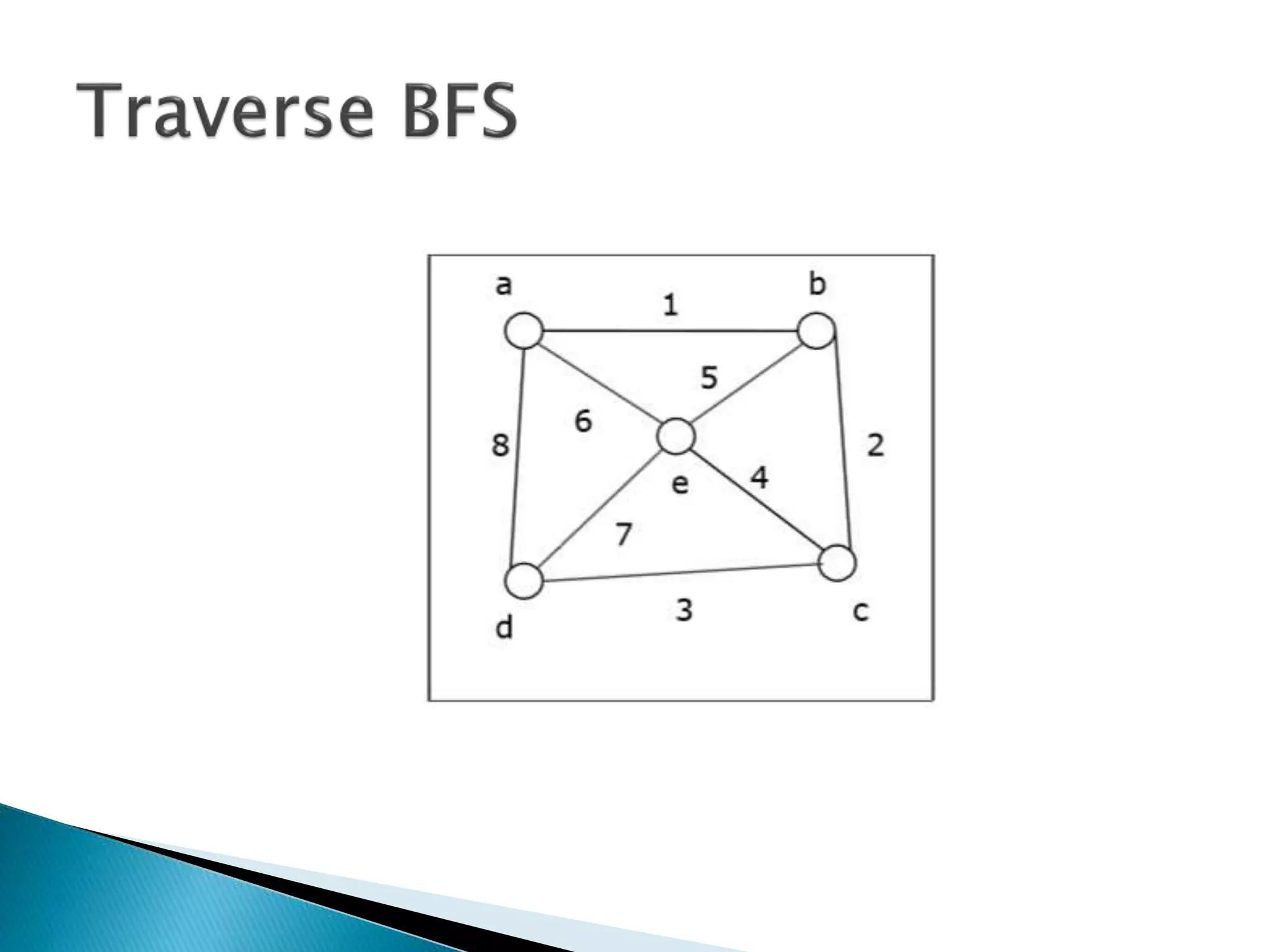
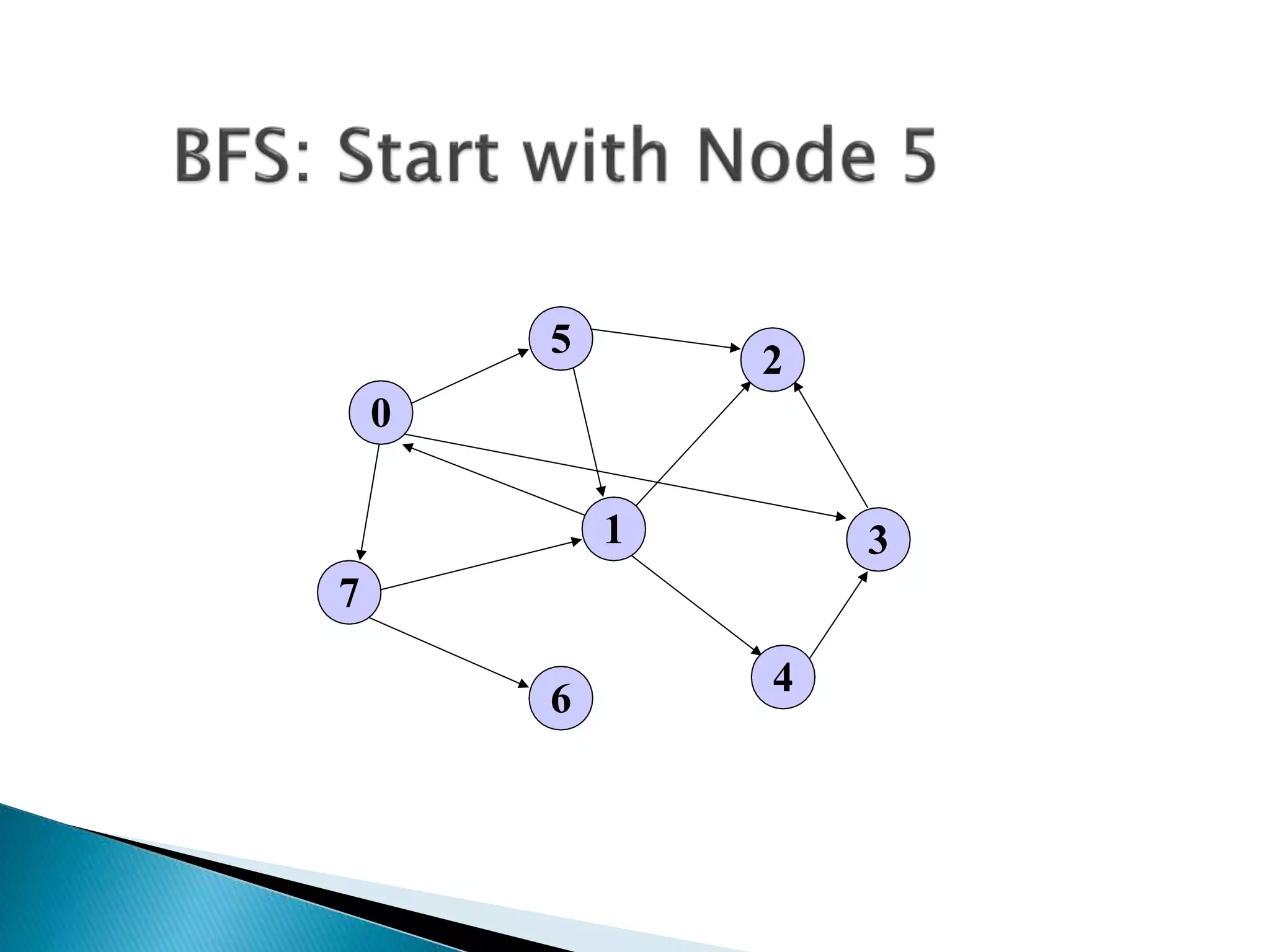
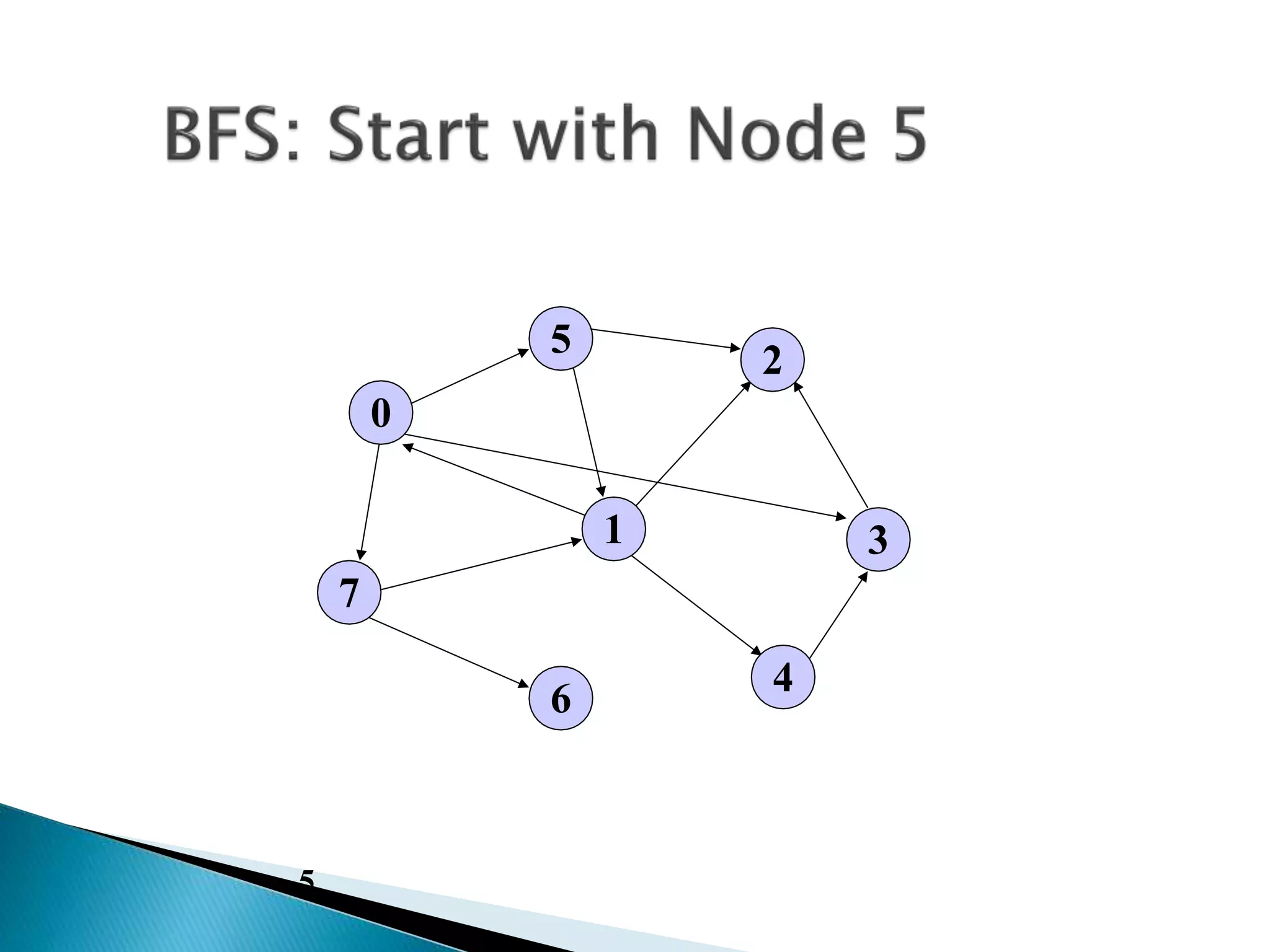
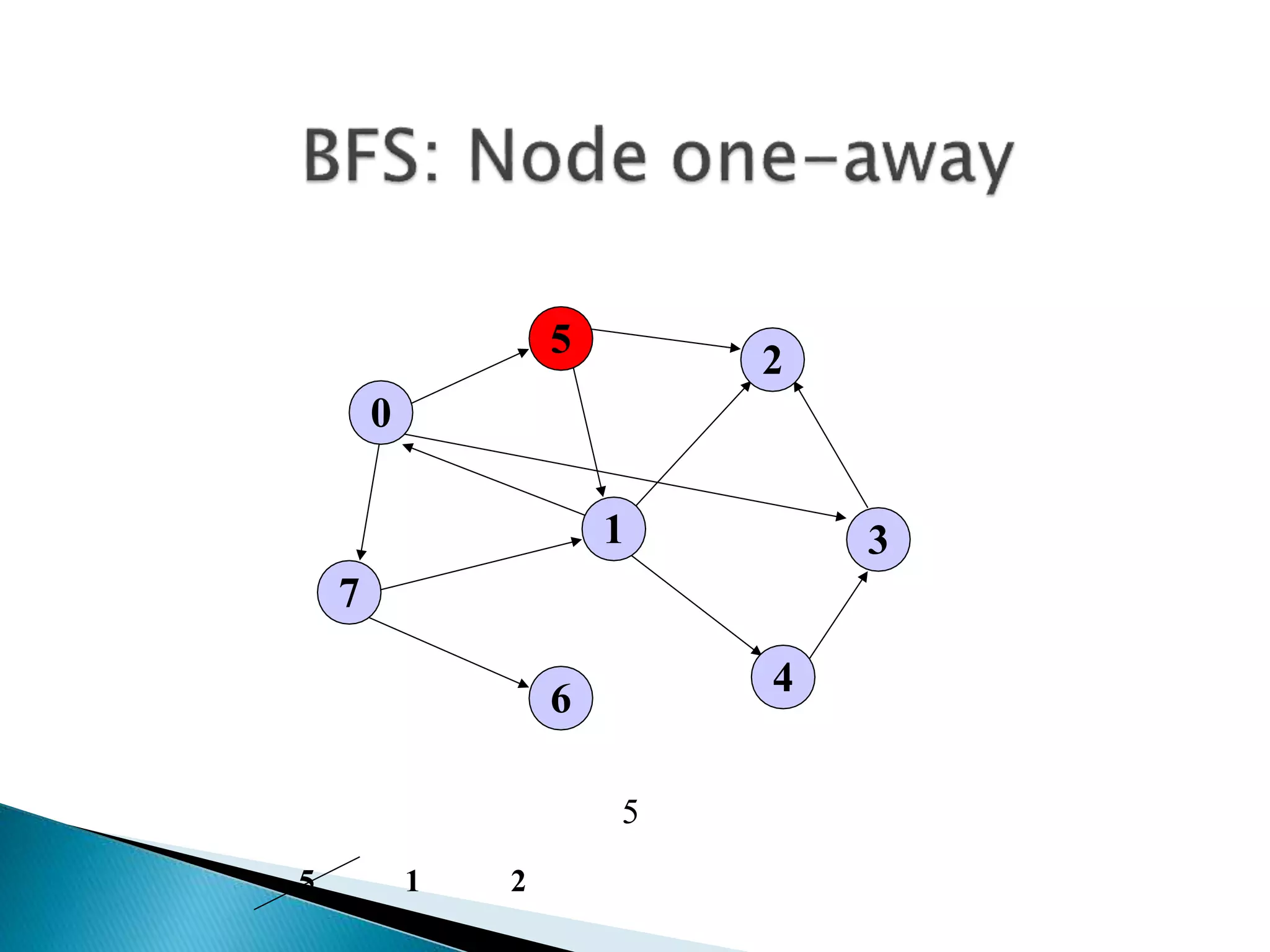
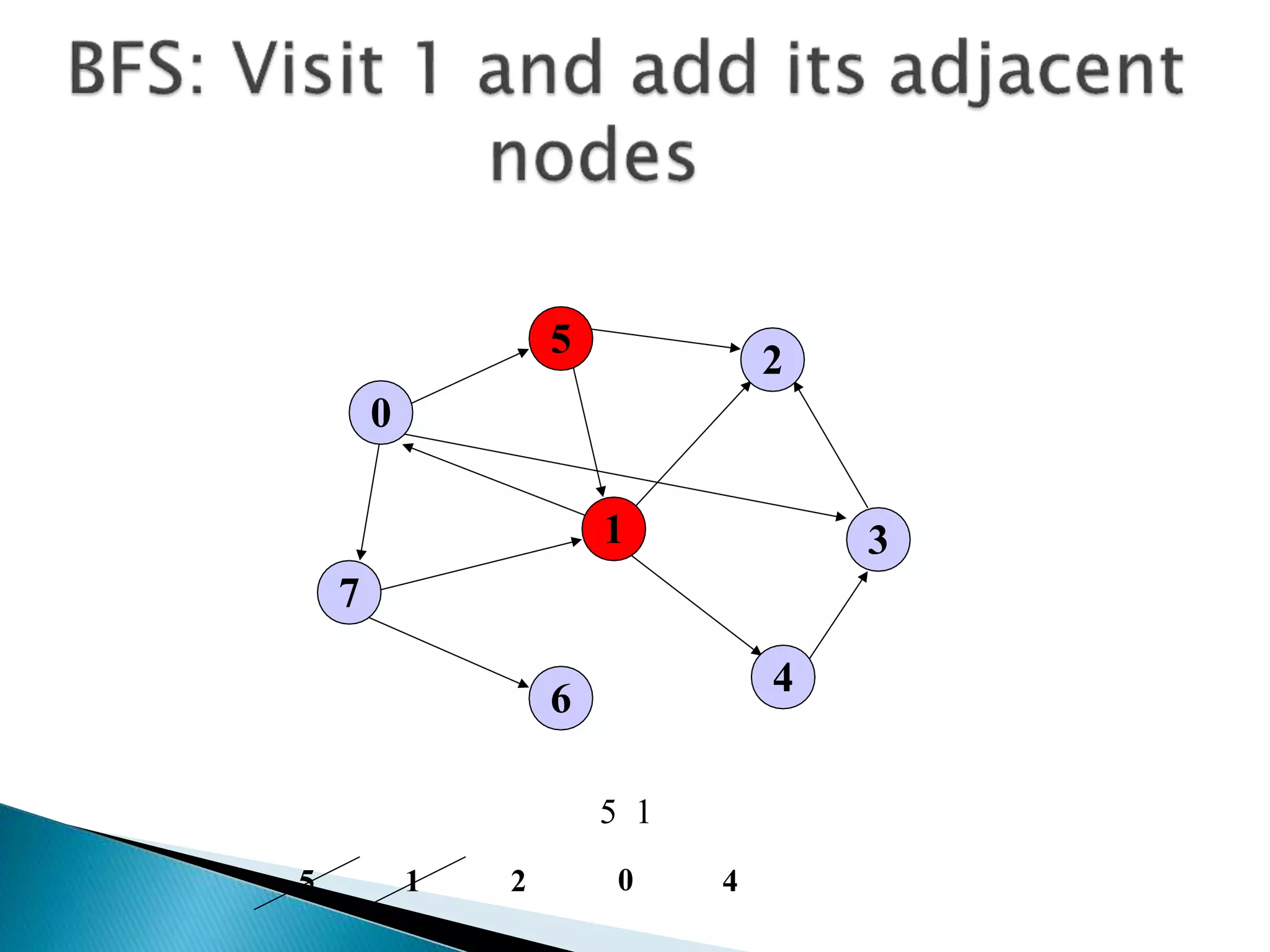
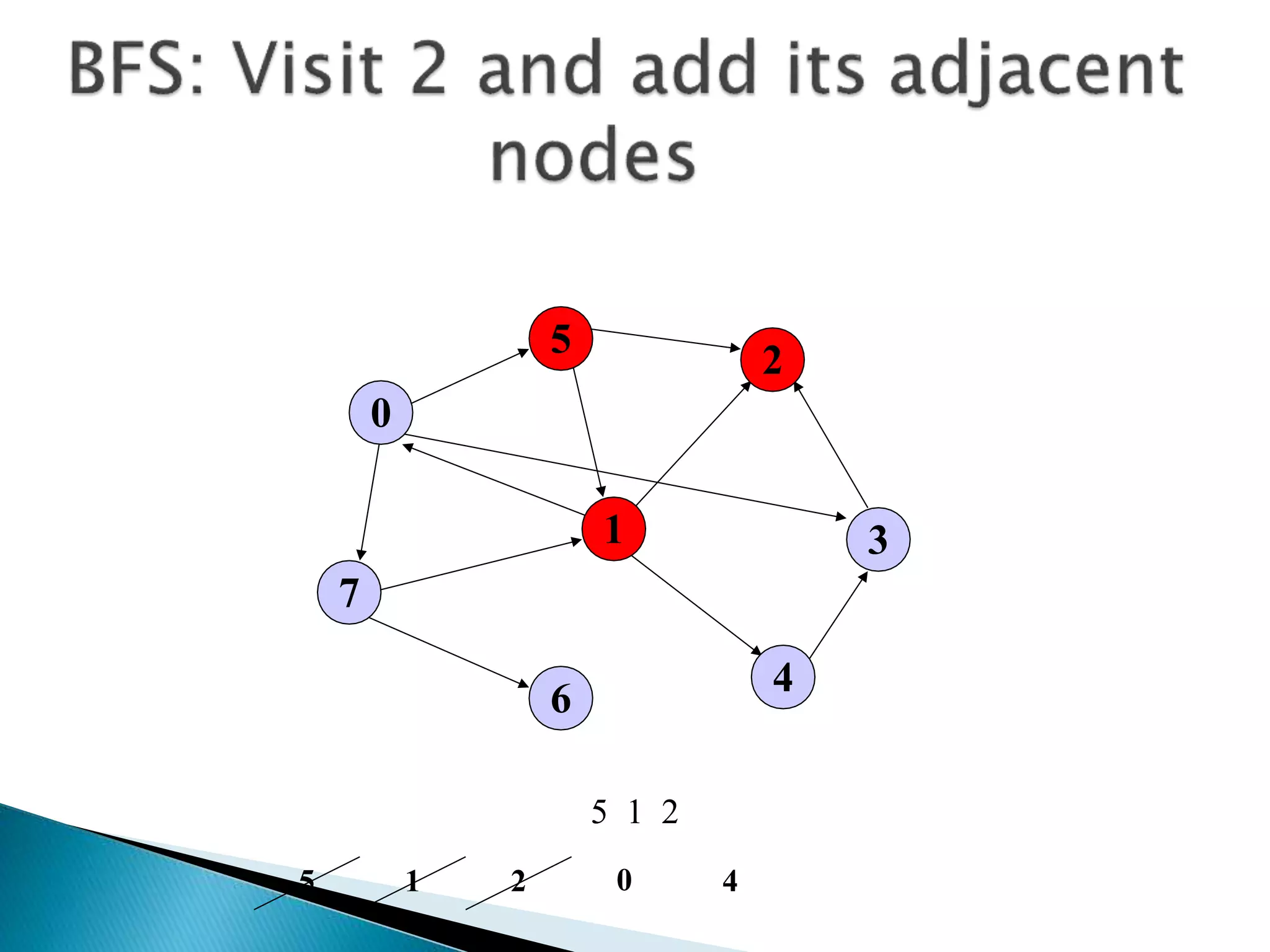
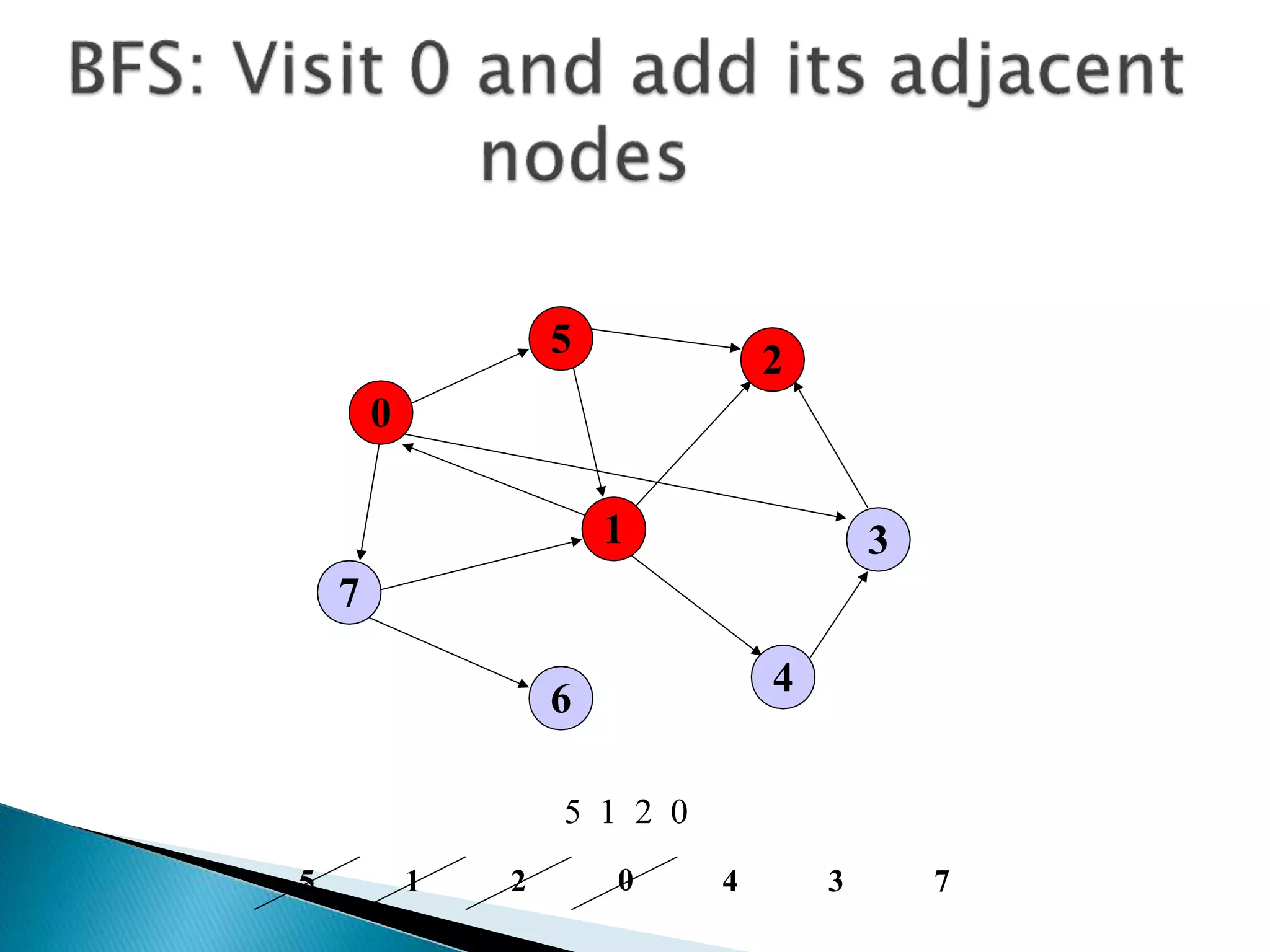
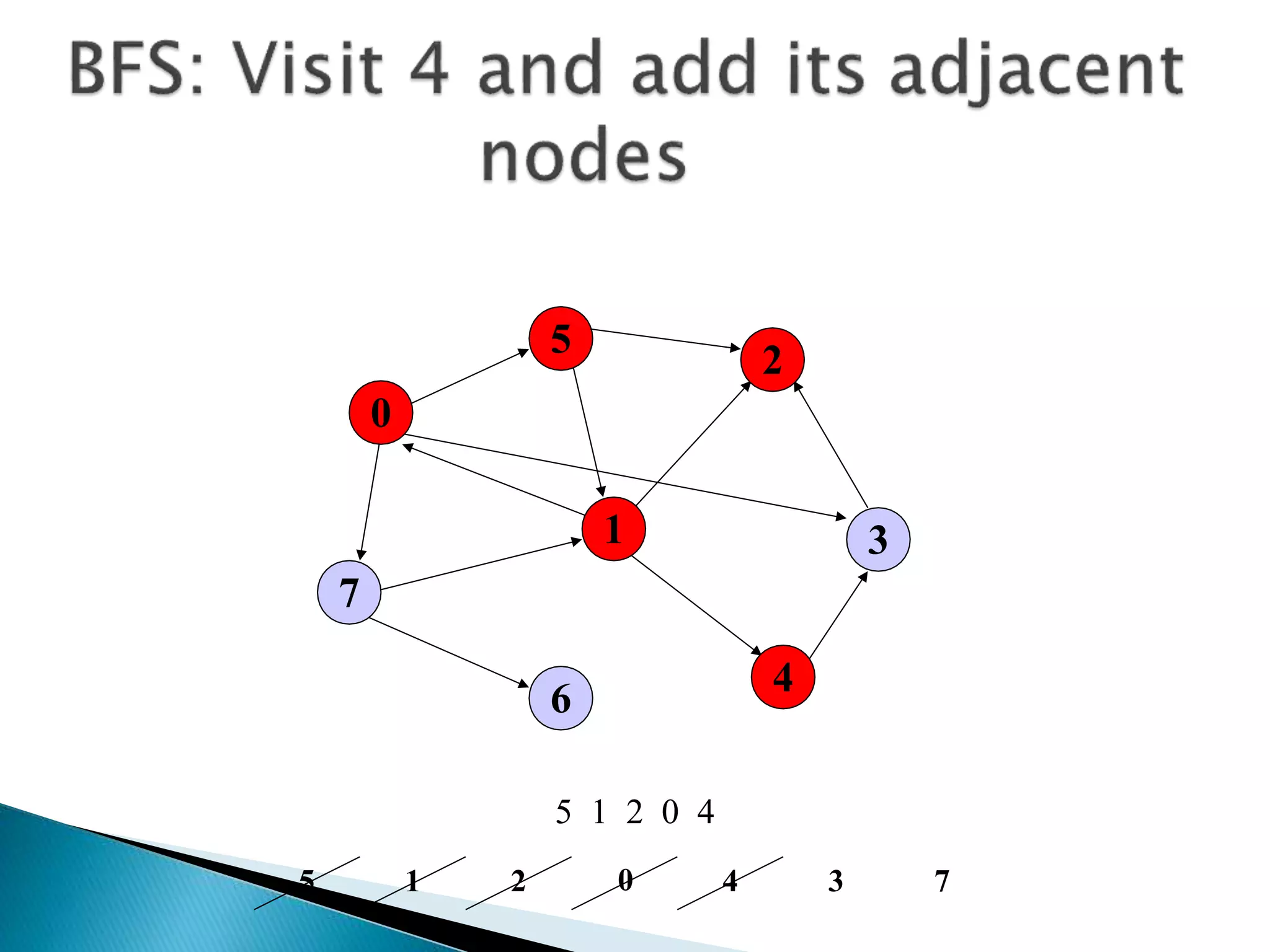
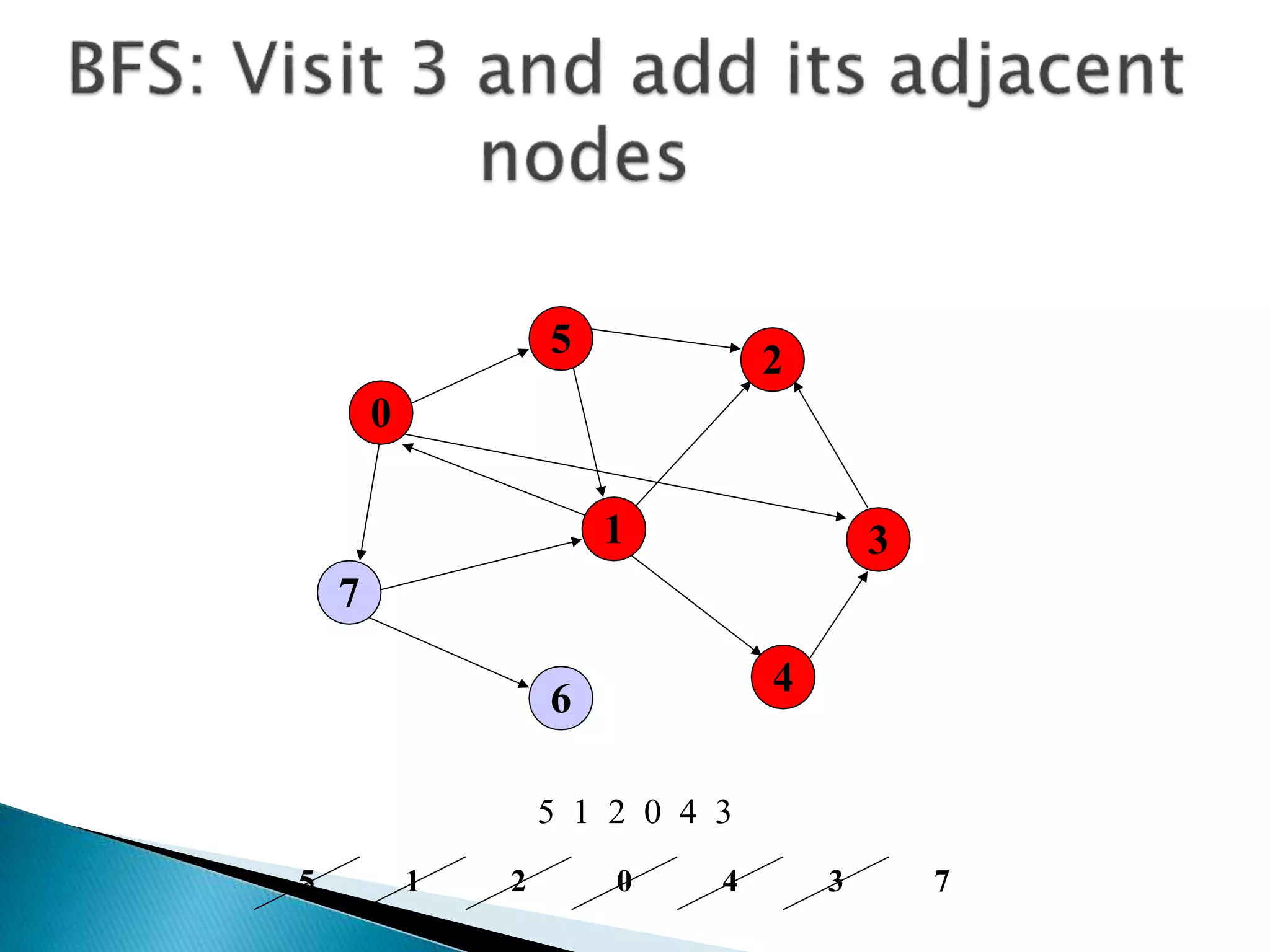
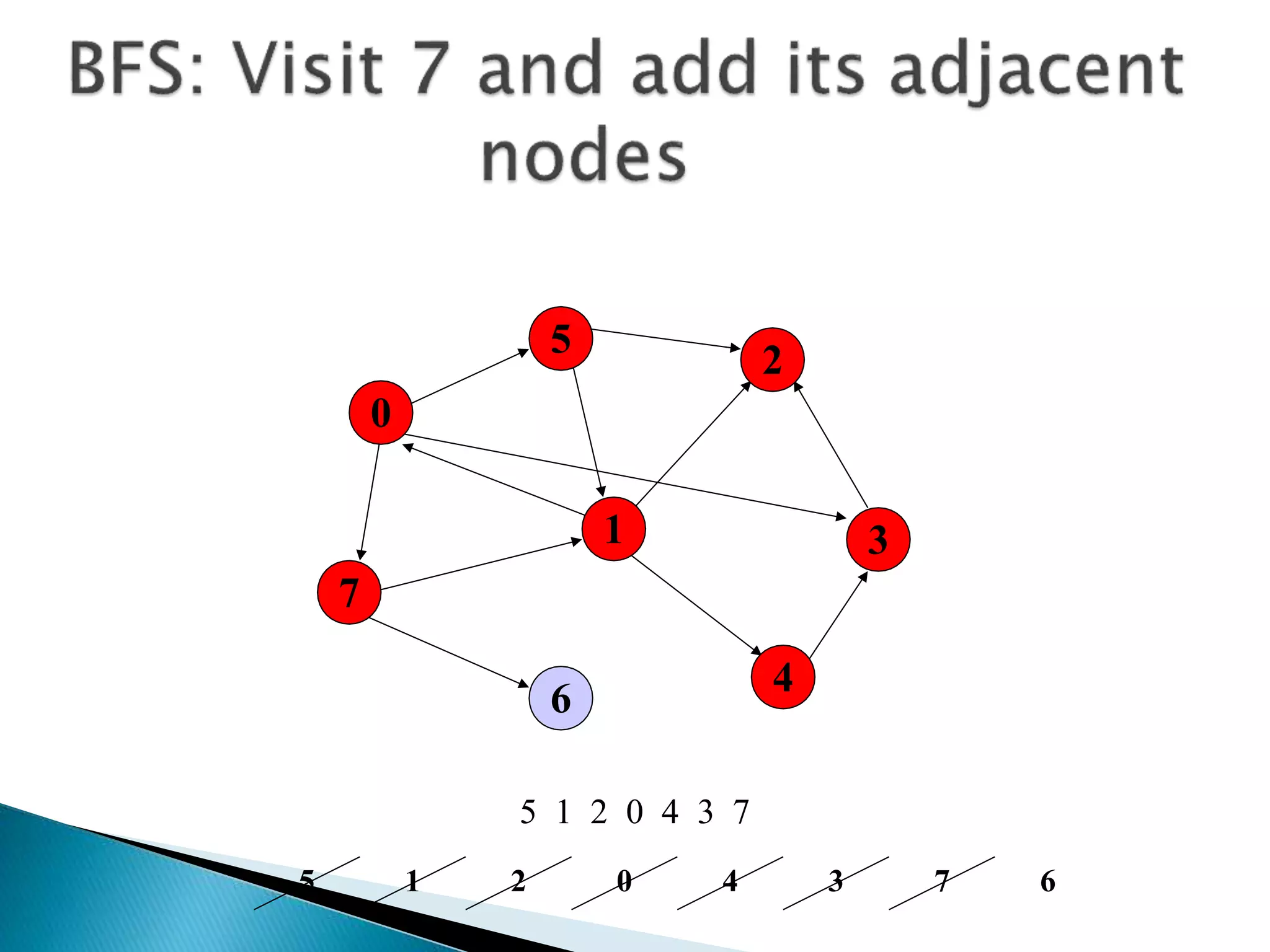
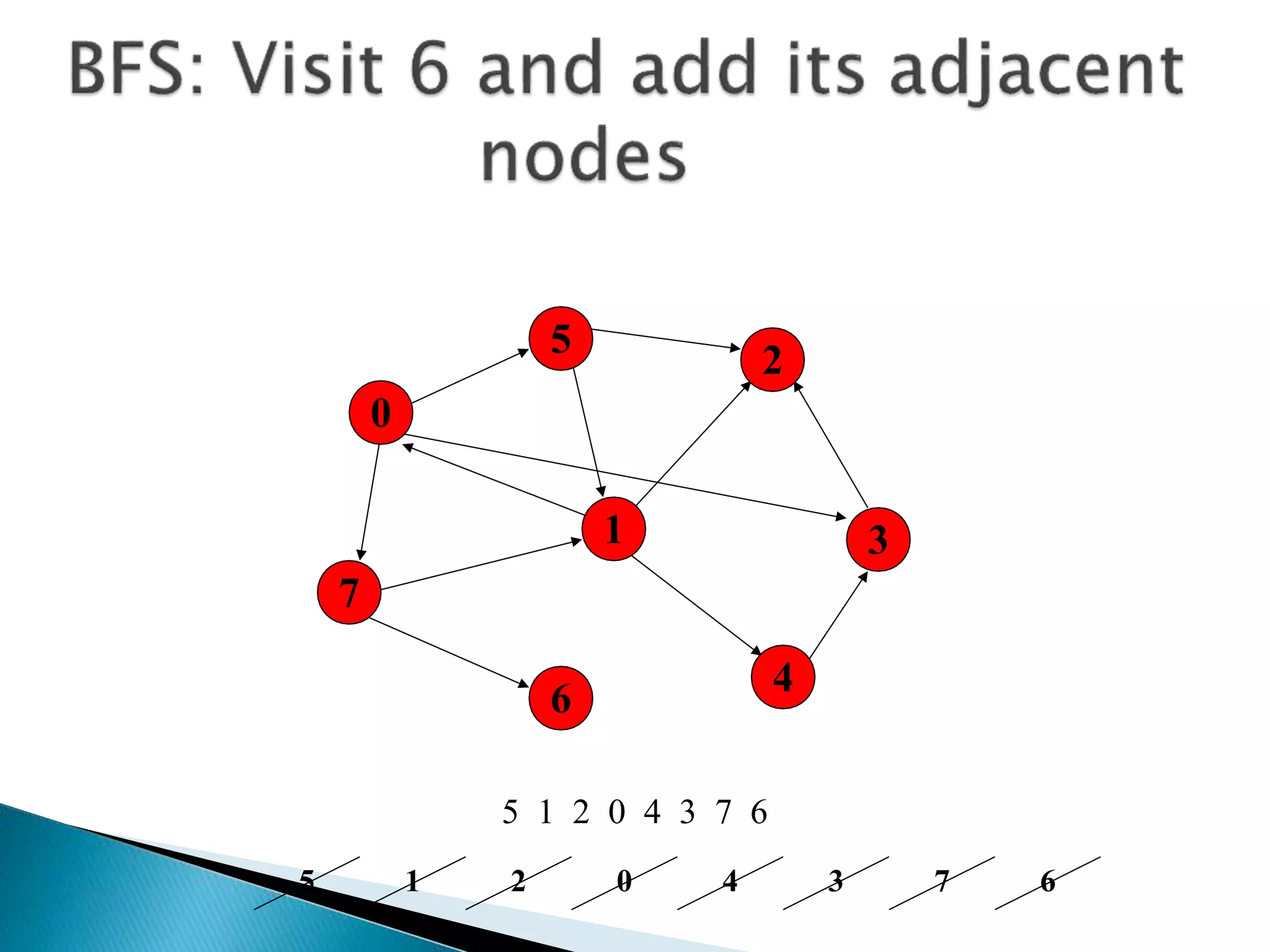
The document discusses graph traversal algorithms depth-first search (DFS) and breadth-first search (BFS). DFS uses a stack and traverses deeper nodes before shallower ones, outputting different traversal orders depending on the starting node. BFS uses a queue and traverses all neighbors of a node before moving to the next level, always outputting the same traversal order. Examples are given of applying DFS and BFS to a sample graph. Applications of the algorithms include computing distances, checking for cycles, and determining reachability between nodes.

1. BY:
Kirti Verma
AP, CSE
LNCTE

2.  Introduction
 Types of graph Traversal
 Depth-First Search
 Breadth-First Search
 Application of BFS and DFS

3. Graph traversal is also known as graph search
refers to the process of visiting each vertex in a graph.
Such traversals are classified by the order in which
the vertices are visited. Tree traversal is a special
case of graph traversal.

4. • Depth-first search (DFS) is an algorithm for traversing
or searching tree or graph data structures.
• DFS uses stack.
• If at any vertex, it encounters that all the adjacent
vertices are visited, then it backtracks until it finds the
first vertex having an adjacent vertex that has not
been traversed before.
• Then, it traverses that vertex, continues with its
adjacent vertices until it traverses all visited vertices
and has to backtrack again.

5. The concept is to visit all the neighbor vertices of a neighbor
vertex before visiting the other neighbor vertices.
 Initialize status of all nodes as “Ready”
 Put source vertex in a stack and change its status to “Waiting”
 Repeat the following two steps until stack is empty −
◦ Pop the top vertex from the stack and mark it as “Visited”
◦ Push onto the top of the stack all neighbors of the removed
vertex whose status is “Ready”. Mark their status as
“Waiting”.

7.  Initialize status of all vertices to “Ready”.
 Push a in stack and change its status to “Waiting”.
 Pop a and mark it as “Visited”.
 Push a’s neighbors in “Ready” state e, d and b to top of stack and
mark them as “Waiting”.
 Pop b from stack, mark it as “Visited”, push its “Ready”
neighbor c onto stack.
 Pop c from stack and mark it as “Visited”. It has no “Ready”
neighbor.
 Pop d from stack and mark it as “Visited”. It has no “Ready”
neighbor.
 Pop e from stack and mark it as “Visited”. It has no “Ready”
neighbor.
 Stack is empty. So stop.

8.  The alternate orders of traversal are −
 a → e → b → c → d
 Or, a → b → e → c → d
 Or, a → d → e → b → c
 Or, a → d → c → e → b
 Or, a → d → c → b → e

9. // recursive, preorder
void dfs (Node v) {
if (v == null)
return;
if (v not yet visited)
visit&mark(v); // visit node before adjacent nodes
for (each w adjacent to v)
if (w has not yet been visited)
dfs(w);
} // dfs

10. 0
7
1
5
4
3
2
6
Policy: Visit adjacent nodes in increasing index order

11. 0
7
1
5
4
3
2
6
5 1 0 3 2 7 6 4

12. 0
7
1
5
4
3
2
6
5
Push 5

13. 0
7
1
5
4
3
2
6
Pop/Visit/Mark5
5

14. 0
7
1
5
4
3
2
6
1
2
5
Push 2, Push 1

15. 0
7
1
5
4
3
2
6
2
Pop/Visit/Mark1
5 1

16. 0
7
1
5
4
3
2
6
0
4
2
5 1
Push 4, Push 0

17. 0
7
1
5
4
3
2
6
4
2
5 1 0
Pop/Visit/Mark0

18. 0
7
1
5
4
3
2
6
3
7
4
2
Push 7, Push 3
5 1 0

19. 0
7
1
5
4
3
2
6
7
4
2
5 1 0 3
Pop/Visit/Mark3

20. 0
7
1
5
4
3
2
6
7
4
2
5 1 0 3
2 is already instack

21. 0
7
1
5
4
3
2
6
7
4
2
Pop/Mark/Visit7
5 1 0 3 7

22. 0
7
1
5
4
3
2
6
6
4
2
5 1 0 3 7
Push 6

23. 0
7
1
5
4
3
2
6
4
2
5 1 0 3 7 6
Pop/Mark/Visit6

24. 0
7
1
5
4
3
2
6
2
Pop/Mark/Visit4
5 1 0 3 7 6 4

25. 0
7
1
5
4
3
2
6
Pop/Mark/Visit2
5 1 0 3 7 6 4 2

26. 0
7
1
5
4
3
2
6
Done
5 1 0 3 7 6 4 2

27. Breadth-first search (BFS) is an algorithm for
traversing or searching tree or graph data structures.
It uses queue.

28.  The concept is to visit all the neighbor vertices
before visiting other neighbor vertices of
neighbor vertices.
 Initialize status of all nodes as “Ready”.
 Put source vertex in a queue and change its
status to “Waiting”.
 Repeat the following two steps until queue is
empty −
◦ Remove the first vertex from the queue and mark it as
“Visited”.
◦ Add to the rear of queue all neighbors of the removed
vertex whose status is “Ready”. Mark their status as
“Waiting”.

30.  Initialize status of all vertices to “Ready”.
 Put a in queue and change its status to “Waiting”.
 Remove a from queue, mark it as “Visited”.
 Add a’s neighbors in “Ready” state b, d and e to end of queue and mark
them as “Waiting”.
 Remove b from queue, mark it as “Visited”, put its “Ready”
neighbor c at end of queue and mark c as “Waiting”.
 Remove d from queue and mark it as “Visited”. It has no neighbor in
“Ready” state.
 Remove e from queue and mark it as “Visited”. It has no neighbor in
“Ready” state.
 Remove c from queue and mark it as “Visited”. It has no neighbor in
“Ready” state.
 Queue is empty so stop.
So the traversal order is −
 a → b → d → e → c

31.  The alternate orders of traversal are −
 a → b → e → d → c
 Or, a → d → b → e → c
 Or, a → e → b → d → c
 Or, a → b → e → d → c
 Or, a → d → e → b → c

32.  // non-recursive, preorder, breadth-first search
void bfs (Node v) {
 if (v == null)
return;
 enqueue(v);
 while (queue is not empty) {
dequeue(v);
 if (v has not yet been visited)
mark&visit(v);
 for (each w adjacent to v)
 if (w has not yet been visited && has not been queued)
enqueue(w);
 } // while
 } // bfs

33. 7
1
5
4
3
2
6
0

34. 7
1
5
4
3
2
6
0
5

35. 7
1
5
4
3
2
6
0
5
5 1 2

36. 7
1
5
4
3
2
6
0
5 1
0
5 1 2 4

37. 7
1
5
4
3
2
6
0
5 1 2
0
5 1 2 4

38. 7
1
5
4
3
2
6
0
5 1 2 0
0
5 1 2 4 3 7

39. 7
1
5
4
3
2
6
0
5 1 2 0 4
0
5 1 2 4 3 7

40. 7
1
5
4
3
2
6
0
5 1 2 0 4 3
5 1 2 0 4 3 7

41. 7
1
5
4
3
2
6
0
5 1 2 0 4 3 7
5 1 2 0 4 3 7 6

42. 7
1
5
4
3
2
6
0
5 1 2 0 4 3 7 6
5 1 2 0 4 3 7 6

43. 7
1
5
4
3
2
6
5 1 2 0 4 3 7 6
0

44. •
•
•
Computing Distances
Checking for cycles in a graph
Reachability: Given a graph G and vertices x and y, determine if there
exists a path from x to y.

45. • Checking for Biconnected Graph: A graph is biconnected if removal of
any vertex does not affect connectivity of the other vertices. Used to
test if network is robust to failure of certain nodes. A single DFS
traversal algorithm.