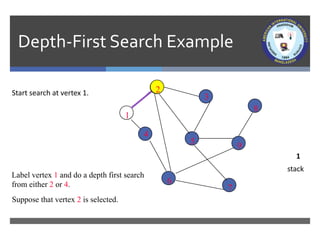
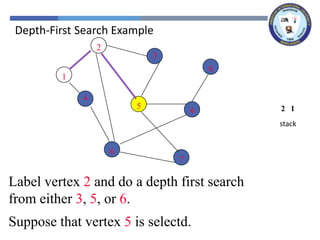
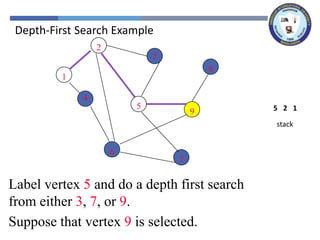
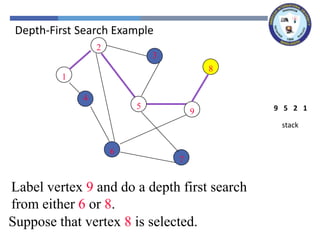
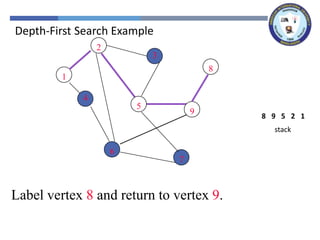
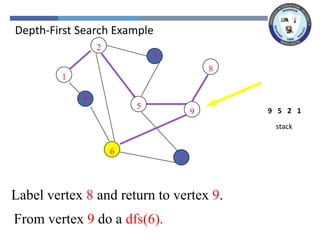
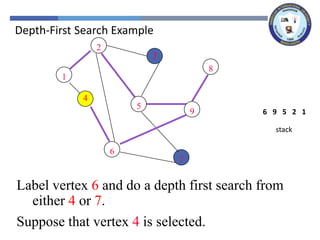
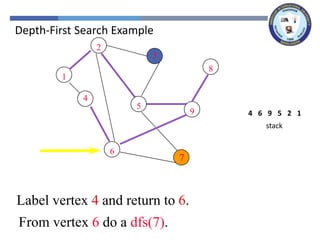
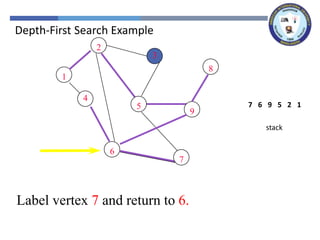
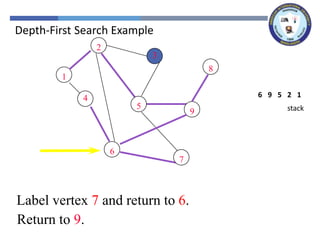
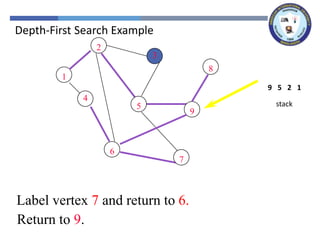
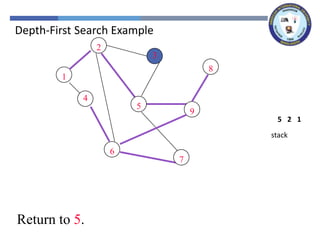
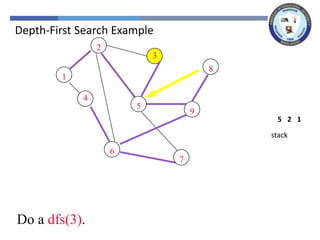
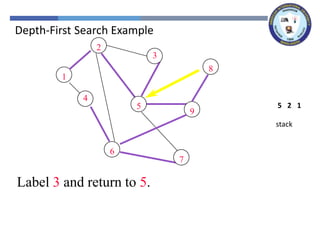
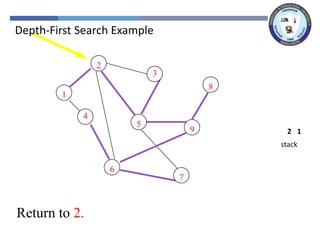
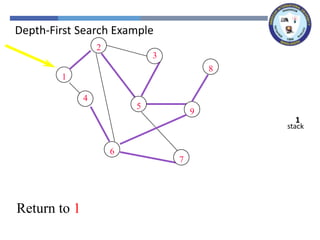
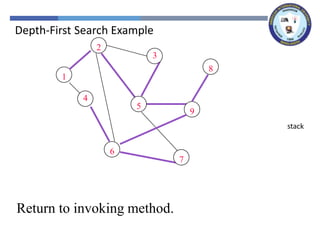
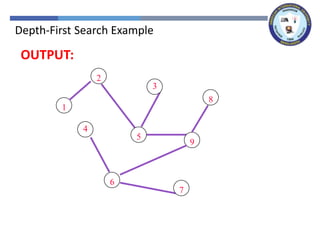
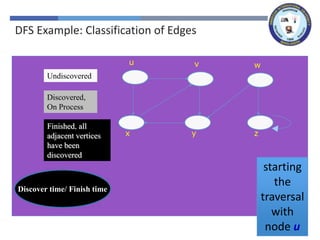
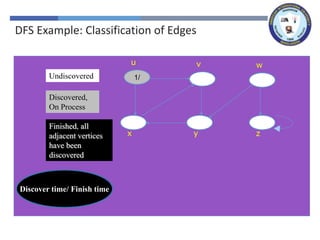
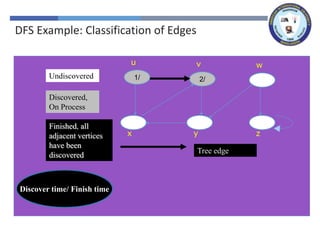
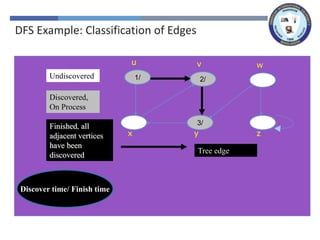
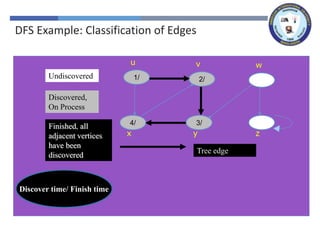
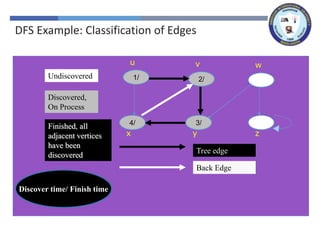
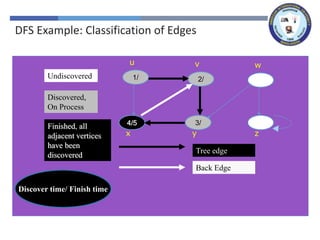
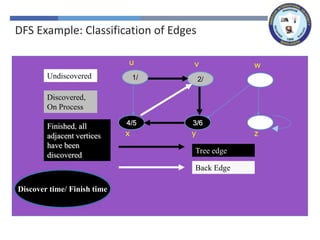
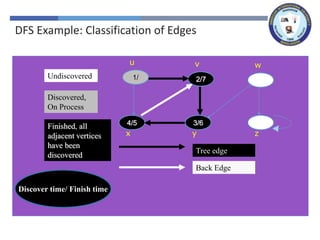
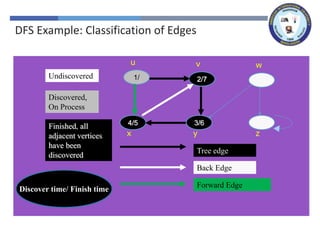
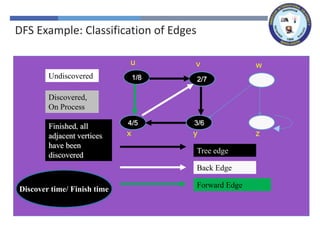
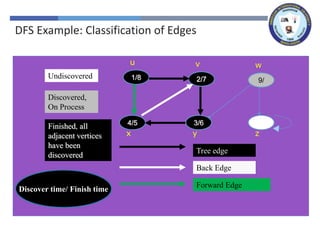
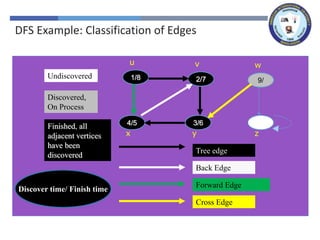
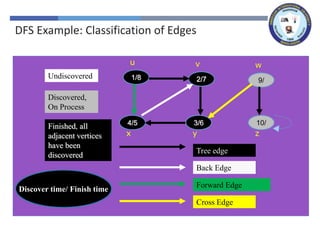
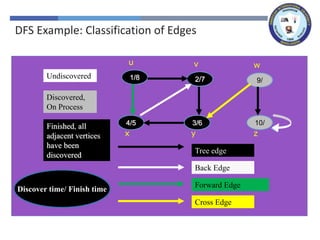
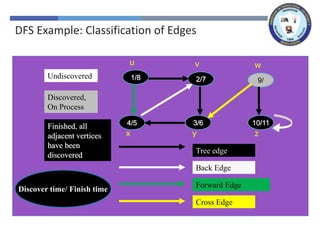
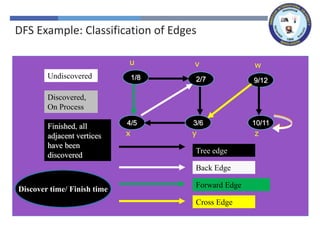
The document outlines a lecture on graph search methods, specifically focusing on depth-first search (DFS) in the context of data structures. It describes the DFS algorithm, examples of traversing graphs, and the classification of edges encountered during the search, such as tree edges, back edges, forward edges, and cross edges. Key concepts include the exploration strategy of DFS, timestamps for discovery and completion, and the implications for understanding graph structures.

1. GraphTraversing and Searching
Course Code: CSC 2106
Dept. of Computer Science
Faculty of Science and Technology
Lecture No: 12.2 Week No: 12 Semester: 21-22 Fall
Lecturer: Dr. Md Mehedi Hasan; mmhasan@aiub.edu
Course Title: Data Structure (Theory)

2. Lecture Outline
1. Graph Search Methods
2. Depth-First-Search (DFS)
3. DFS Example

3. Graph Search Methods
Given: a graph G = (V, E), directed or undirected
Goal: methodically explore every vertex and edge
Ultimately: build a tree on the graph
 Pick a vertex as the root
 Choose certain edges to produce a tree
 Note: might also build a forest if graph is not connected

4. Graph Search Methods
 Many graph problems solved using a search method.
 Path from one vertex to another.
 Is the graph connected?
 Find a spanning tree.
 Etc.
 Commonly used search methods:
 Depth-first search.
 Breadth-first search.
 Other variants: best-first, iterated deepening search, etc.

5. Depth-First Search
depthFirstSearch(v)
{
Label vertex v as reached.
for (each unreached vertex u
adjacenct from v)
depthFirstSearch(u);
}

6. Depth-First Search Example
Suppose that vertex 2 is selected.
2
3
8
1
4
5
9
6
7
1
2
1
stack
Start search at vertex 1.
Label vertex 1 and do a depth first search
from either 2 or 4.

7. Depth-First Search Example
2
3
8
1
4
5
9
6
7
Label vertex 2 and do a depth first search
from either 3, 5, or 6.
1
2
2
5
stack
Suppose that vertex 5 is selectd.

8. 2
3
8
1
4
5
9
6
7
Label vertex 5 and do a depth first search
from either 3, 7, or 9.
1
2
2
5
5
9
Suppose that vertex 9 is selected.
stack
1
2
5
Depth-First Search Example

9. Label vertex 9 and do a depth first search
from either 6 or 8.
Suppose that vertex 8 is selected.
stack
1
2
5
9
2
3
8
1
4
5
9
6
7
1
2
2
5
5
9
9
8
Depth-First Search Example

10. 2
3
8
1
4
5
9
6
7
Label vertex 8 and return to vertex 9.
1
2
2
5
5
9
9
8
8
6
stack
1
2
5
9
8
Depth-First Search Example

11. 2
3
8
1
4
5
9
6
7
Label vertex 8 and return to vertex 9.
1
2
2
5
5
9
9
8
8
From vertex 9 do a dfs(6).
6
stack
1
2
5
9
Depth-First Search Example

12. 2
3
8
1
4
5
9
6
7
1
2
2
5
5
9
9
8
8
Label vertex 6 and do a depth first search from
either 4 or 7.
6
6
4
Suppose that vertex 4 is selected.
stack
1
2
5
9
6
Depth-First Search Example

13. 2
3
8
1
4
5
9
6
7
1
2
2
5
5
9
9
8
8
Label vertex 4 and return to 6.
6
6
4
4
From vertex 6 do a dfs(7).
7
stack
1
2
5
9
6
4
Depth-First Search Example

14. 2
3
8
1
4
5
9
6
7
1
2
2
5
5
9
9
8
8
Label vertex 7 and return to 6.
6
6
4
4
7
7
stack
1
2
5
9
6
7
Depth-First Search Example

15. 2
3
8
1
4
5
9
6
7
1
2
2
5
5
9
9
8
8
Label vertex 7 and return to 6.
6
6
4
4
7
7
Return to 9.
stack
1
2
5
9
6
Depth-First Search Example

16. 2
3
8
1
4
5
9
6
7
1
2
2
5
5
9
9
8
8
Label vertex 7 and return to 6.
6
6
4
4
7
7
Return to 9.
stack
1
2
5
9
Depth-First Search Example

17. 2
3
8
1
4
5
9
6
7
1
2
2
5
5
9
9
8
8
6
6
4
4
7
7
Return to 5.
stack
1
2
5
Depth-First Search Example

18. 2
3
8
1
4
5
9
6
7
1
2
2
5
5
9
9
8
8
6
6
4
4
7
7
Do a dfs(3).
3
stack
1
2
5
Depth-First Search Example

19. 2
3
8
1
4
5
9
6
7
1
2
2
5
5
9
9
8
8
6
6
4
4
7
7
Label 3 and return to 5.
3
3
stack
1
2
5
Depth-First Search Example

20. 2
3
8
1
4
5
9
6
7
1
2
2
5
5
9
9
8
8
6
6
4
4
7
7
3
3
Return to 2.
stack
1
2
Depth-First Search Example

21. 2
3
8
1
4
5
9
6
7
1
2
2
5
5
9
9
8
8
6
6
4
4
7
7
3
3
Return to 1
stack
1
Depth-First Search Example

22. 2
3
8
1
4
5
9
6
7
1
2
2
5
5
9
9
8
8
6
6
4
4
7
7
3
3
Return to invoking method.
stack
Depth-First Search Example

23. 1
2
5
9
8
6
4
7
3
OUTPUT:
Depth-First Search Example

24. Depth-First Search
 Explore “deeper” in the graph whenever possible - (Follows LIFO
mechanism)
 Edges are explored/visited out of the most recently discovered vertex v that
still has unexplored/unvisited edges.
 When all of v’s edges have been explored, backtrack to the vertex from which
v was discovered.
 computes 2 timestamps: 𝒅( ) (discovered) and 𝒇( ) (finished)
 builds one or more depth-first tree(s) (depth-first forest)
 Algorithm colors each vertex
 WHITE: undiscovered
 GRAY: discovered, in process
 BLACK: finished, all adjacent vertices have been discovered

25. DFS: Classification of Edges
 DFS can be used to classify edges of G:
 Tree edges: Edges in the depth-first forest.
 Back edges: Edges (u, v) connecting a vertex u to an ancestor v in a
depth-first tree (where v is not the parent of u). It also applies for
self loops.
 Forward edges: Non-tree edges (u, v) connecting a vertex u to a
descendant v in a depth-first tree.
 Cross edges: All other edges.
 DFS yields valuable information about the structure of a graph.
 In DFS of an undirected graph we get only tree and back edges; no
forward or back-edges.

26. DFS Example: Classification of Edges
x z
y
w
v
u
Undiscovered
Discovered,
On Process
Finished, all
adjacent vertices
have been
discovered
Discover time/ Finish time
starting
the
traversal
with
node u

27. x z
y
w
v
u
x z
y
w
v
1/
u
Undiscovered
Discovered,
On Process
Finished, all
adjacent vertices
have been
discovered
Discover time/ Finish time
DFS Example: Classification of Edges

28. x z
y
w
v
u
x z
y
w
v
1/
u
x z
y
w
2/
v
1/
u
Tree edge
Undiscovered
Discovered,
On Process
Finished, all
adjacent vertices
have been
discovered
Discover time/ Finish time
DFS Example: Classification of Edges

29. x z
y
w
v
u
x z
y
w
v
1/
u
x z
y
w
2/
v
1/
u
Tree edge
x z
3/
y
w
2/
v
1/
u
Undiscovered
Discovered,
On Process
Finished, all
adjacent vertices
have been
discovered
Discover time/ Finish time
DFS Example: Classification of Edges

30. x z
y
w
v
u
x z
y
w
v
1/
u
x z
y
w
2/
v
1/
u
Tree edge
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
Undiscovered
Discovered,
On Process
Finished, all
adjacent vertices
have been
discovered
Discover time/ Finish time
DFS Example: Classification of Edges

31. x z
y
w
v
u
x z
y
w
v
1/
u
x z
y
w
2/
v
1/
u
Tree edge
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
Back Edge
Undiscovered
Discovered,
On Process
Finished, all
adjacent vertices
have been
discovered
Discover time/ Finish time
DFS Example: Classification of Edges

32. x z
y
w
v
u
x z
y
w
v
1/
u
x z
y
w
2/
v
1/
u
Tree edge
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
Back Edge
4/5
x z
3/
y
w
2/
v
1/
u
Undiscovered
Discovered,
On Process
Finished, all
adjacent vertices
have been
discovered
Discover time/ Finish time
DFS Example: Classification of Edges

33. x z
y
w
v
u
x z
y
w
v
1/
u
x z
y
w
2/
v
1/
u
Tree edge
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
Back Edge
4/5
x z
3/
y
w
2/
v
1/
u
4/5
x z
3/6
y
w
2/
v
1/
u
Undiscovered
Discovered,
On Process
Finished, all
adjacent vertices
have been
discovered
Discover time/ Finish time
DFS Example: Classification of Edges

34. x z
y
w
v
u
x z
y
w
v
1/
u
x z
y
w
2/
v
1/
u
Tree edge
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
Back Edge
4/5
x z
3/
y
w
2/
v
1/
u
4/5
x z
3/6
y
w
2/
v
1/
u
4/5
x z
3/6
y
w
2/7
v
1/
u
Undiscovered
Discovered,
On Process
Finished, all
adjacent vertices
have been
discovered
Discover time/ Finish time
DFS Example: Classification of Edges

35. x z
y
w
v
u
x z
y
w
v
1/
u
x z
y
w
2/
v
1/
u
Tree edge
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
Back Edge
4/5
x z
3/
y
w
2/
v
1/
u
4/5
x z
3/6
y
w
2/
v
1/
u
4/5
x z
3/6
y
w
2/7
v
1/
u
4/5
x z
3/6
y
w
2/7
v
1/8
u
4/5
x z
3/6
y
w
2/7
v
1/
u
Forward Edge
Undiscovered
Discovered,
On Process
Finished, all
adjacent vertices
have been
discovered
Discover time/ Finish time
DFS Example: Classification of Edges

36. x z
y
w
v
u
x z
y
w
v
1/
u
x z
y
w
2/
v
1/
u
Tree edge
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
Back Edge
4/5
x z
3/
y
w
2/
v
1/
u
4/5
x z
3/6
y
w
2/
v
1/
u
4/5
x z
3/6
y
w
2/7
v
1/
u
4/5
x z
3/6
y
w
2/7
v
1/8
u
Undiscovered
Discovered,
On Process
Finished, all
adjacent vertices
have been
discovered
4/5
x z
3/6
y
w
2/7
v
1/8
u
Forward Edge
Discover time/ Finish time
DFS Example: Classification of Edges

37. x z
y
w
v
u
x z
y
w
v
1/
u
x z
y
w
2/
v
1/
u
Tree edge
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
Back Edge
4/5
x z
3/
y
w
2/
v
1/
u
4/5
x z
3/6
y
w
2/
v
1/
u
4/5
x z
3/6
y
w
2/7
v
1/
u
4/5
x z
3/6
y
w
2/7
v
1/8
u
4/5
x z
3/6
y
w
2/7
v
1/8
u
Forward Edge
4/5
x z
3/6
y
9/
w
2/7
v
1/8
u
Undiscovered
Discovered,
On Process
Finished, all
adjacent vertices
have been
discovered
Discover time/ Finish time
DFS Example: Classification of Edges

38. x z
y
w
v
u
x z
y
w
v
1/
u
x z
y
w
2/
v
1/
u
Tree edge
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
Back Edge
4/5
x z
3/
y
w
2/
v
1/
u
4/5
x z
3/6
y
w
2/
v
1/
u
4/5
x z
3/6
y
w
2/7
v
1/
u
4/5
x z
3/6
y
w
2/7
v
1/8
u
4/5
x z
3/6
y
w
2/7
v
1/8
u
Forward Edge
4/5
x z
3/6
y
9/
w
2/7
v
1/8
u
4/5
x z
3/6
y
9/
w
2/7
v
1/8
u
Cross Edge
Undiscovered
Discovered,
On Process
Finished, all
adjacent vertices
have been
discovered
Discover time/ Finish time
DFS Example: Classification of Edges

39. x z
y
w
v
u
x z
y
w
v
1/
u
x z
y
w
2/
v
1/
u
Tree edge
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
Back Edge
4/5
x z
3/
y
w
2/
v
1/
u
4/5
x z
3/6
y
w
2/
v
1/
u
4/5
x z
3/6
y
w
2/7
v
1/
u
4/5
x z
3/6
y
w
2/7
v
1/8
u
4/5
x z
3/6
y
w
2/7
v
1/8
u
Forward Edge
4/5
x z
3/6
y
9/
w
2/7
v
1/8
u
4/5
x z
3/6
y
9/
w
2/7
v
1/8
u
Cross Edge
4/5
x
10/
z
3/6
y
9/
w
2/7
v
1/8
u
Undiscovered
Discovered,
On Process
Finished, all
adjacent vertices
have been
discovered
Discover time/ Finish time
DFS Example: Classification of Edges

40. x z
y
w
v
u
x z
y
w
v
1/
u
x z
y
w
2/
v
1/
u
Tree edge
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
Back Edge
4/5
x z
3/
y
w
2/
v
1/
u
4/5
x z
3/6
y
w
2/
v
1/
u
4/5
x z
3/6
y
w
2/7
v
1/
u
4/5
x z
3/6
y
w
2/7
v
1/8
u
4/5
x z
3/6
y
w
2/7
v
1/8
u
Forward Edge
4/5
x z
3/6
y
9/
w
2/7
v
1/8
u
4/5
x z
3/6
y
9/
w
2/7
v
1/8
u
Cross Edge
4/5
x
10/
z
3/6
y
9/
w
2/7
v
1/8
u
4/5
x
10/
z
3/6
y
9/
w
2/7
v
1/8
u
Undiscovered
Discovered,
On Process
Finished, all
adjacent vertices
have been
discovered
Discover time/ Finish time
DFS Example: Classification of Edges

41. x z
y
w
v
u
x z
y
w
v
1/
u
x z
y
w
2/
v
1/
u
Tree edge
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
Back Edge
4/5
x z
3/
y
w
2/
v
1/
u
4/5
x z
3/6
y
w
2/
v
1/
u
4/5
x z
3/6
y
w
2/7
v
1/
u
4/5
x z
3/6
y
w
2/7
v
1/8
u
4/5
x z
3/6
y
w
2/7
v
1/8
u
Forward Edge
4/5
x z
3/6
y
9/
w
2/7
v
1/8
u
4/5
x z
3/6
y
9/
w
2/7
v
1/8
u
Cross Edge
4/5
x
10/
z
3/6
y
9/
w
2/7
v
1/8
u
4/5
x
10/
z
3/6
y
9/
w
2/7
v
1/8
u
4/5
x
10/11
z
3/6
y
9/
w
2/7
v
1/8
u
Undiscovered
Discovered,
On Process
Finished, all
adjacent vertices
have been
discovered
Discover time/ Finish time
DFS Example: Classification of Edges

42. x z
y
w
v
u
x z
y
w
v
1/
u
x z
y
w
2/
v
1/
u
Tree edge
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
4/
x z
3/
y
w
2/
v
1/
u
Back Edge
4/5
x z
3/
y
w
2/
v
1/
u
4/5
x z
3/6
y
w
2/
v
1/
u
4/5
x z
3/6
y
w
2/7
v
1/
u
4/5
x z
3/6
y
w
2/7
v
1/8
u
4/5
x z
3/6
y
w
2/7
v
1/8
u
Forward Edge
4/5
x z
3/6
y
9/
w
2/7
v
1/8
u
4/5
x z
3/6
y
9/
w
2/7
v
1/8
u
Cross Edge
4/5
x
10/
z
3/6
y
9/
w
2/7
v
1/8
u
4/5
x
10/
z
3/6
y
9/
w
2/7
v
1/8
u
4/5
x
10/11
z
3/6
y
9/
w
2/7
v
1/8
u
4/5
x
10/11
z
3/6
y
9/12
w
2/7
v
1/8
u
Undiscovered
Discovered,
On Process
Finished, all
adjacent vertices
have been
discovered
Discover time/ Finish time
DFS Example: Classification of Edges

43. Applications of Depth First Search
 For a weighted graph, DFS traversal of the graph produces the
minimum spanning tree and all pair shortest path tree
 Detecting cycle in a graph
 Path Finding
 Topological Sorting
 To test if a graph is bipartite
 Finding Strongly Connected Components of a graph
 Solving puzzles with only one solution, such as mazes.

44. Books
 “Schaum's Outline of Data Structures with C++”. By John R. Hubbard (Can be
found in university Library)
 “Data Structures and Program Design”, Robert L. Kruse, 3rd Edition, 1996.
 “Data structures, algorithms and performance”, D. Wood, Addison-Wesley, 1993
 “Advanced Data Structures”, Peter Brass, Cambridge University Press, 2008
 “Data Structures and Algorithm Analysis”, Edition 3.2 (C++ Version), Clifford A.
Shaffer, Virginia Tech, Blacksburg, VA 24061 January 2, 2012
 “C++ Data Structures”, Nell Dale and David Teague, Jones and Bartlett Publishers,
2001.
 “Data Structures and Algorithms with Object-Oriented Design Patterns in C++”,
Bruno R. Preiss,

45. References
1. https://en.wikipedia.org/wiki/Data_structure
2. https://visualgo.net/en/dfsbfs?slide=1