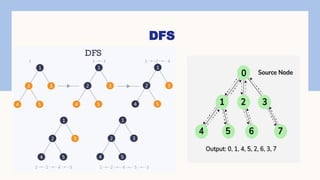
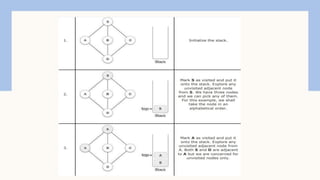
The document explains the depth-first search (DFS) algorithm for graph traversal, emphasizing its systematic approach to visiting vertices using a stack. It outlines the key rules for implementation, including visiting unvisited adjacent vertices and backtracking when necessary. A step-by-step algorithm is provided for initializing vertex states and processing them until the stack is empty.

1. DEPTH FIRST SEARCH ( DFS )

2. GRAPH TRAVERSAL
• Traversal of a graph is a systematic walk that visits all the vertices in a specific order.
• There are mainly two different ways of traversing a graph :
a) Breadth-first traversal
b) Depth-first traversal
• Depth First Search (DFS) algorithm traverses a graph in a depthward motion and
uses a stack
to remember to get the next vertex to start a search, when a dead end occurs in
any iteration.
• DFS uses the idea of backtracking.

3. DFS

4. IMPLEMENTATION
• Rule 1 Visit the adjacent unvisited vertex. Mark it as visited. Display it. Push it in a
−
stack.
• Rule 2 If no adjacent vertex is found, pop up a vertex from the stack. (It will pop
−
up all the
vertices from the stack, which do not have adjacent vertices.)
• Rule 3 Repeat Rule 1 and Rule 2 until the stack is empty
−

6. As C does not have any
unvisited adjacent node so
we keep popping the stack
until we find a node that has
an unvisited adjacent node.
In this case, there's none and
we keep popping until the
stack is empty.

7. ALGORITHM
• Step 1 - Initialize all the vertices to ready state (STATUS = 1)
• Step 2 - Put the starting vertex into STACK and change its status to waiting (STATUS = 2)
• Step 3 - Repeat Steps 4 and 5 until STACK is EMPTY
• Step 4 - POP the top vertex from STACK, Process the vertex, Change its status to processed
state (STATUS = 3)
• Step 5 - PUSH all the neighbors in the ready state (STATUS = 1) to the STACK and change their
status to the waiting state (STATUS = 2)
• Step 6 - Exit.