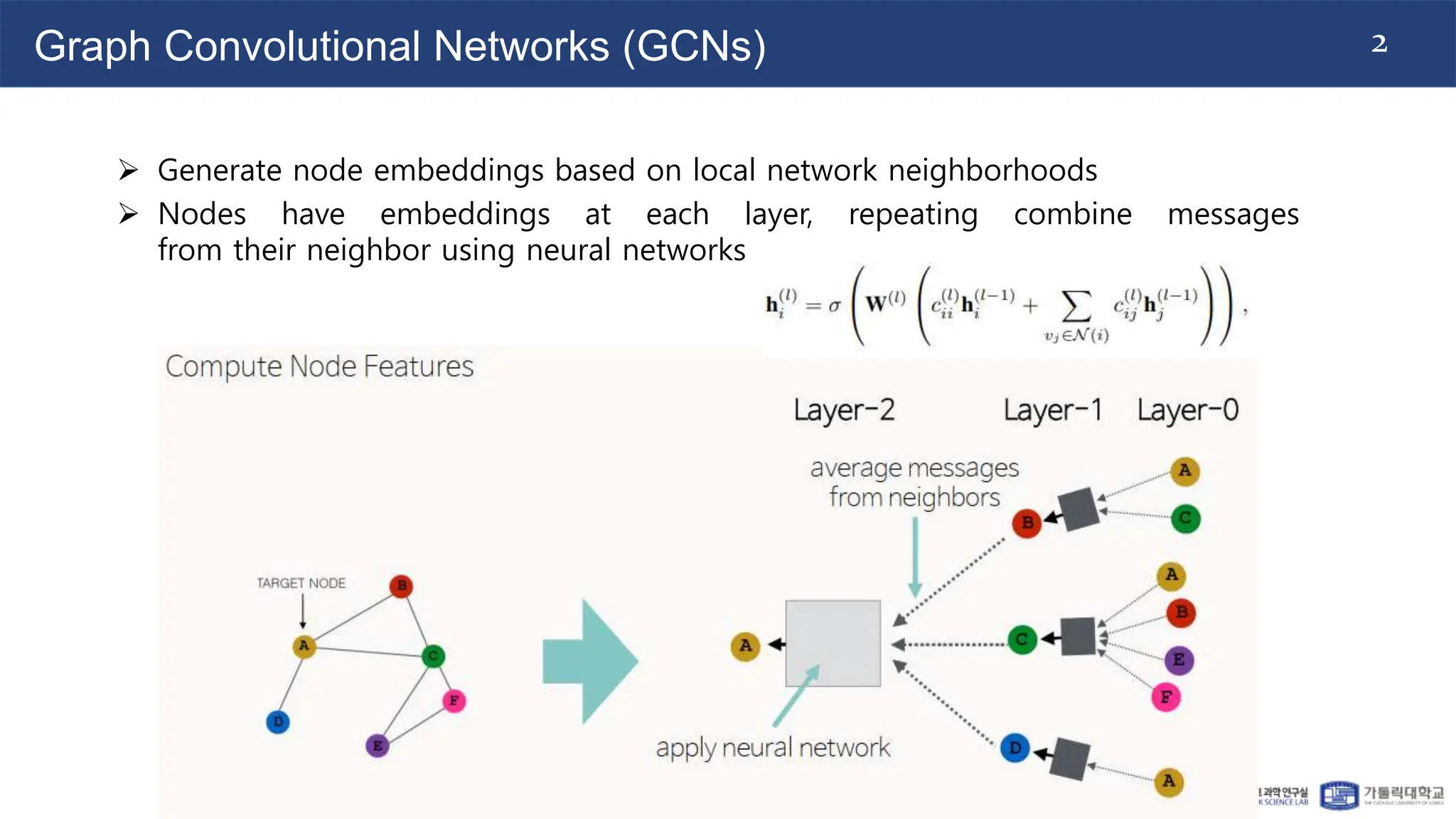
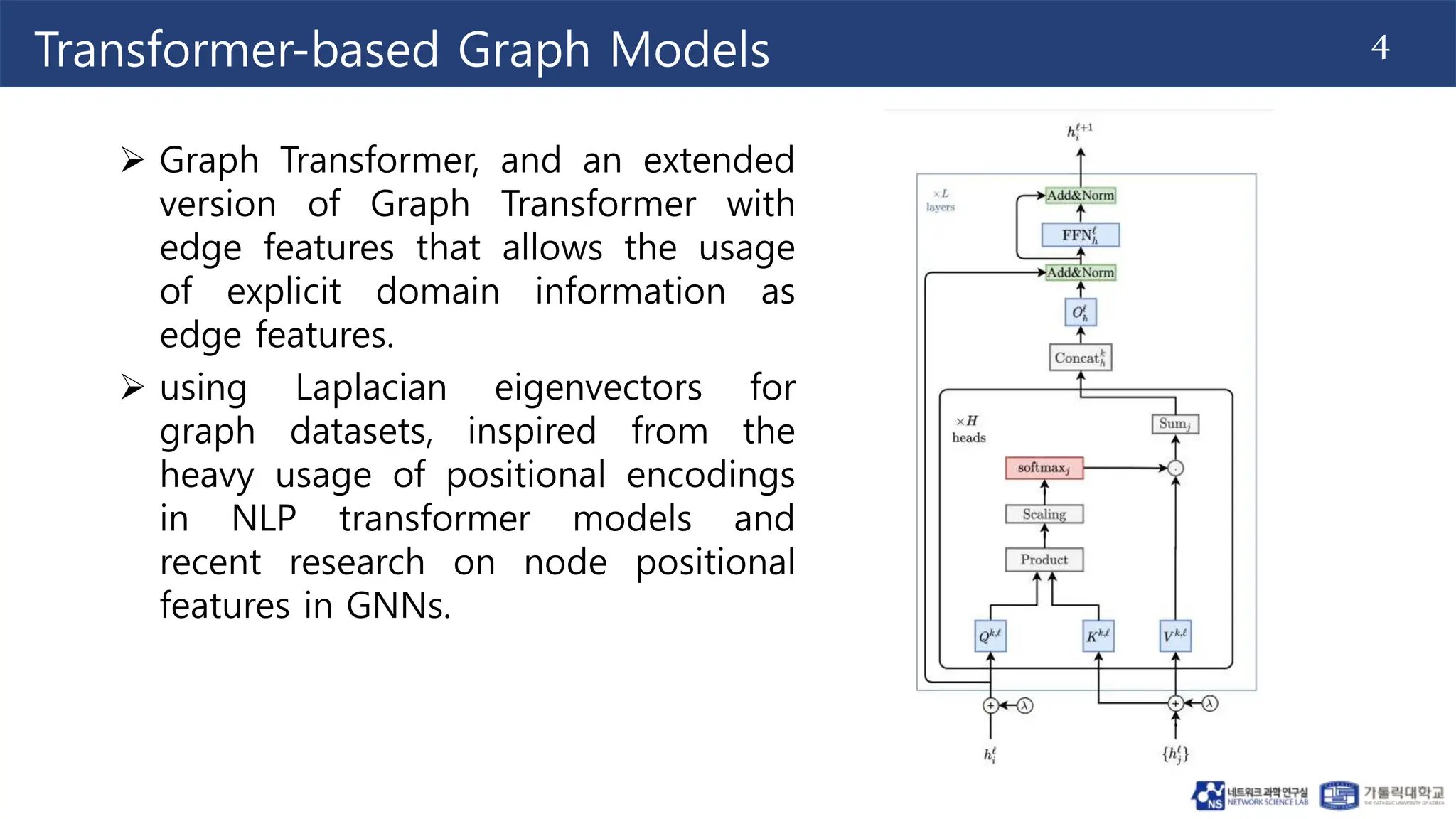
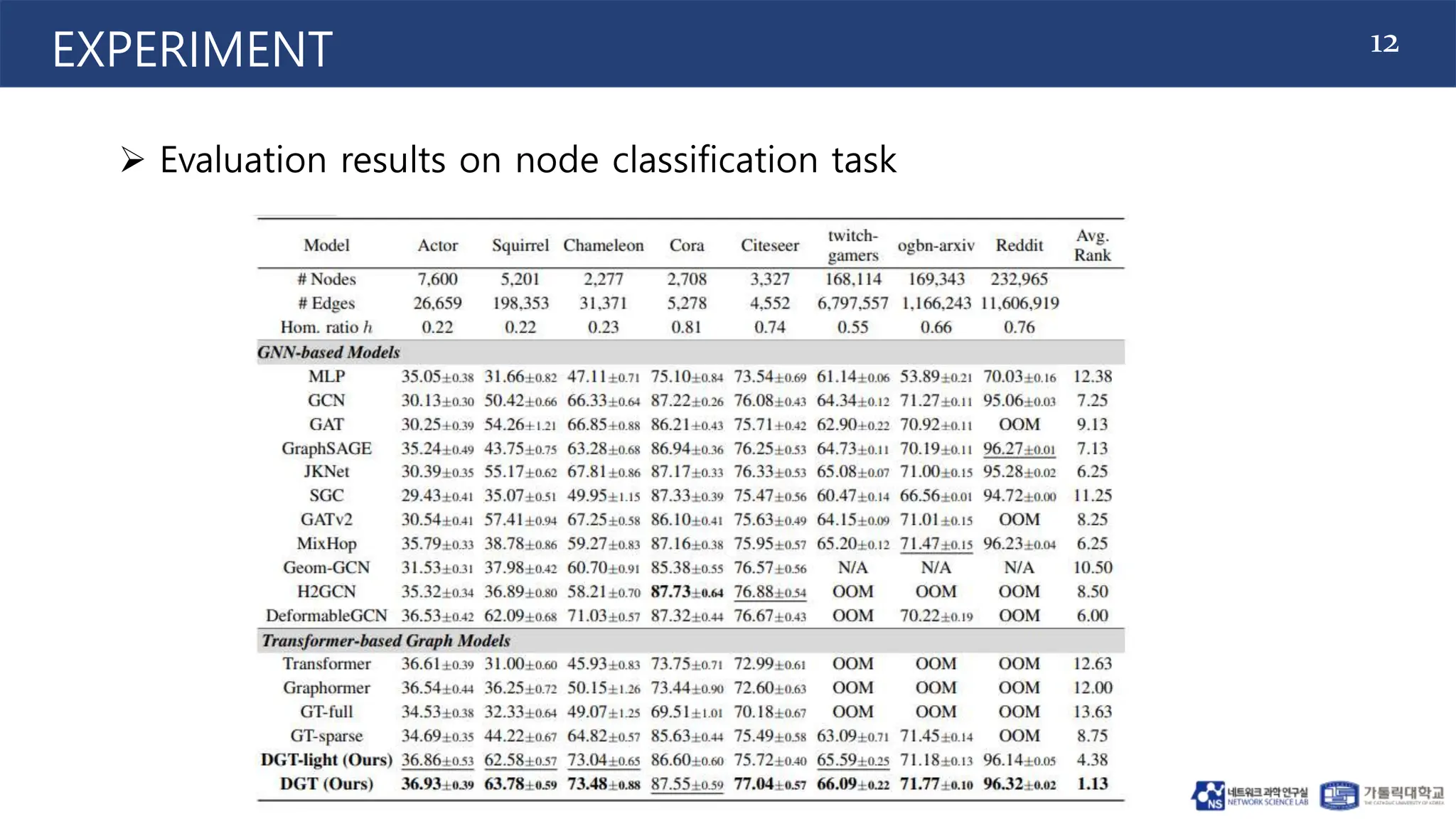
This document proposes the Deformable Graph Transformer (DGT) model, which uses a technique called Deformable Graph Attention (DGA) to perform sparse attention on graphs. DGA flexibly attends to relevant nodes based on their proximity, using multiple sorted node sequences. It also introduces learnable positional encodings called Katz PE that reflect positional information through paths between nodes. The document evaluates DGT on node classification tasks and finds it outperforms other transformer-based graph models while addressing scalability issues.

1. Van Thuy Hoang
Network Science Lab
Dept. of Artificial Intelligence
The Catholic University of Korea
E-mail: hoangvanthuy90@gmail.com
2023-12-26
Jinyoung Park, et. al. AAAI-22

2. 2
Graph Convolutional Networks (GCNs)
 Generate node embeddings based on local network neighborhoods
 Nodes have embeddings at each layer, repeating combine messages
from their neighbor using neural networks

3. 3
Key Contributions
 Deformable Graph Transformer (DGT) performs sparse attention with
a reduced number of keys and values for learning node
representations
 DGA, that flexibly attends to a small set of relevant nodes based on
various types of the proximity between nodes
 Learnable positional encodings named Katz PE

4. 4
Transformer-based Graph Models
 Graph Transformer, and an extended
version of Graph Transformer with
edge features that allows the usage
of explicit domain information as
edge features.
 using Laplacian eigenvectors for
graph datasets, inspired from the
heavy usage of positional encodings
in NLP transformer models and
recent research on node positional
features in GNNs.

5. 5
Overview of the DGA modules
 In pre-processing, NodeSort module first constructs multiple node
sequences (sorting nodes through diverse criteria π)
 Kernel-based interpolation is applied on each offset to get values,
whose offsets are computed by the queries with a linear projection.
 Attention module aggregates the values of each head

6. 6
Overview of the DGA modules
 Multi-Head Attention (MHA) for Transformer-based graph models

7. 7
DEFORMABLE GRAPH ATTENTION
 What we want: finding context nodes
 A NodeSort module that converts a graph into a sorted sequence
of nodes in a regular space
 Given a target node, NodeSort sorts nodes and returns a sequence
of their features

8. 8
DEFORMABLE GRAPH ATTENTION
 Given the set of sorted sequences:
 DGA is defined as:
z_q: features of query node
denotes the representation of the k-th key
node feature at a i-th index of the sequence
kernel-based interpolation:

9. 9
KATZ POSITIONAL ENCODING
 PEs reflect domain-specific positional information into its attention
mechanism.
 Counts all paths between nodes with the decaying weight β to reflect
the preference for shorter paths

10. 10
DEFORMABLE GRAPH TRANSFORMER
 Inputs: . Deformable Graph Transformer first encodes node feature xi
with the learnable function fθ, which can be MLP, and combines with
positional embeddings:
 Given a set of sorted sequences:

11. 11
COMPLEXITY ANALYSIS
 Suppose that N is the number of nodes, C is the dimensionality of
hidden representations.
 The self-attention operation requires a huge computation cost with
the complexity:

12. 12
EXPERIMENT
 Evaluation results on node classification task

13. 13
EXPERIMENT
 Performance comparisons on different ordering and criteria
absolute ordering with random permutation (AR),
absolute ordering with BFS (AB),
absolute ordering with multiple criteria (AM),
relative ordering with BFS (RB),
relative ordering with multiple criteria (RM)

14. 14
CONCLUSION
 DGT that performs sparse attention, named Deformable Graph
Attention (DGA) for learning node representations on large-scale
graphs.
 address two limitations of Transformer-based graph models such as a
scalability issue and aggregation of noisy information.
 Attention considers both structural and semantic proximity based on
diverse node sequences.