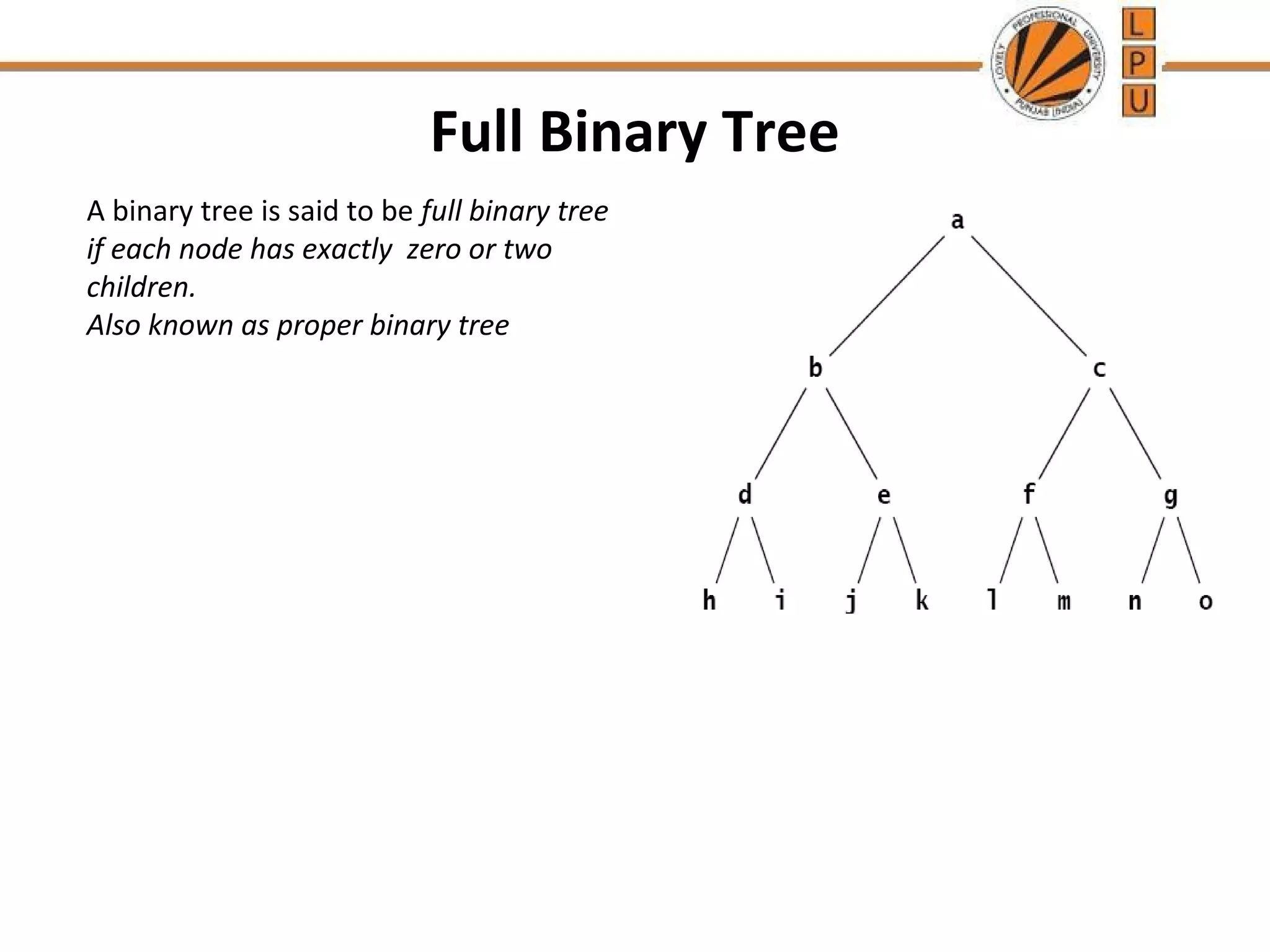
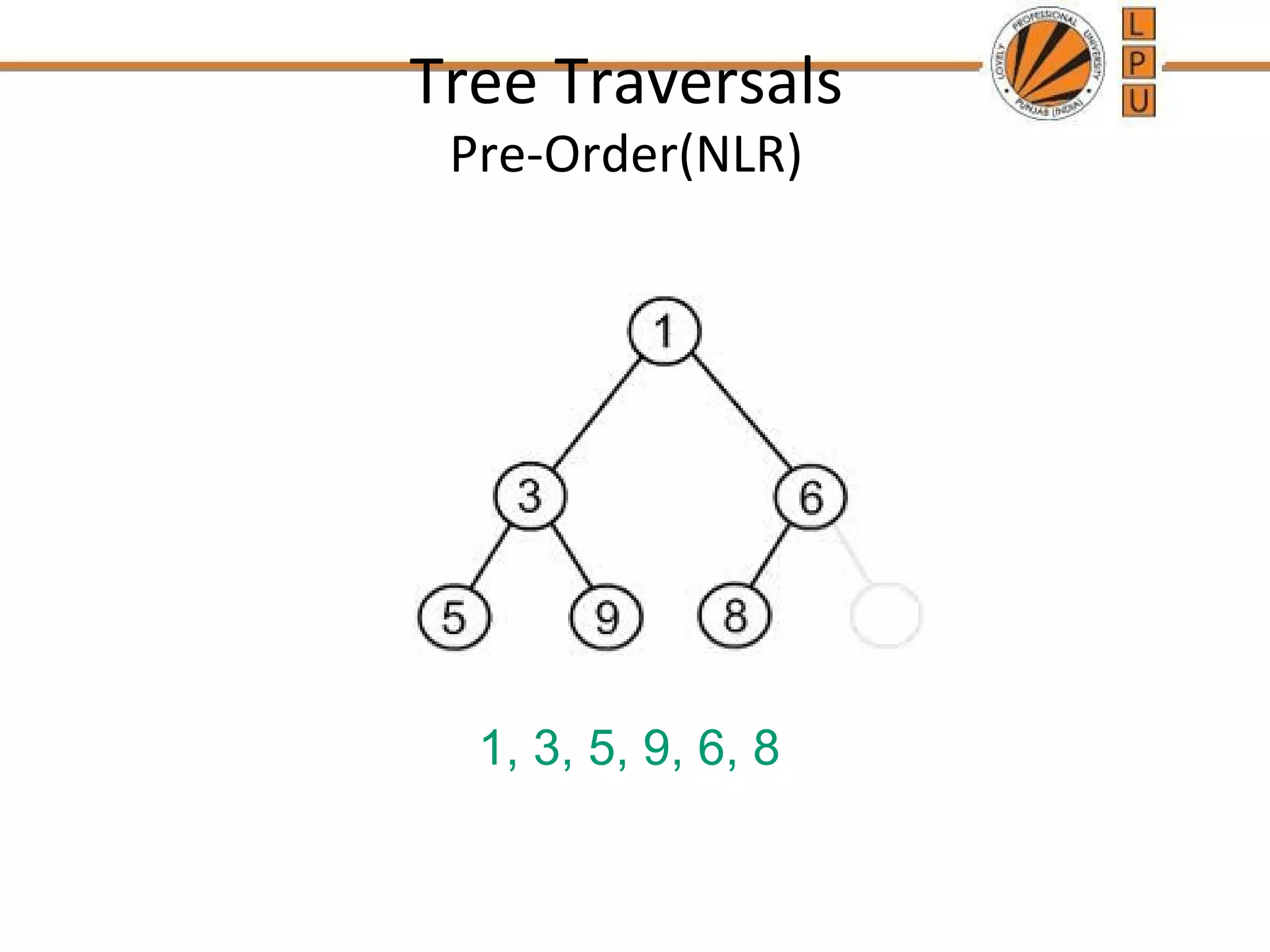
The document discusses trees and binary trees. It defines key tree terminology like nodes, edges, root, leaf, etc. It explains properties of binary trees including full, complete, and binary search trees. It describes techniques for traversing binary trees including preorder, inorder and postorder traversal using recursion and stacks. Searching and insertion operations in binary search trees are also summarized.










![• 4.if n is the number of nodes and e is the number of
edges in an non-empty binary tree then n=e+1.
• 5.if n0 is the number of leaf nodes (no child) and n2 is
the number of nodes with two children in a non-empty
binary tree then n0= n2+1
• 6.for a complete binary tree T with n nodes ,the
height is floor[log2(n+1) -1]](https://image.slidesharecdn.com/trees-141206172727-conversion-gate02/75/Trees-12-2048.jpg)











![• 1.[Initiaaly push NULL onto STACK and initialize
PTR]
Set TOP1.STACK[1]NULL and PTRROOT
2.Repeat steps 3 to 5 while PTR!=NULL
3.Apply PROCESS to INFO[PTR]
4.[Right Child?]
If RIGHT[PTR]!=NULL [Push on STACK]
TOPTOP+1
STACK[TOP]RIGHT[PTR]
[End of if structure]](https://image.slidesharecdn.com/trees-141206172727-conversion-gate02/75/Trees-25-2048.jpg)
![• 5.[Left Child ?]
If LEFT[PTR]!=NULL,
Set PTRLEFT[PTR]
Else [pop from stack]
PTRSTACK[TOP]
TOPTOP-1
[End of if strucutre]
[End of step 2 loop]
6.Exit](https://image.slidesharecdn.com/trees-141206172727-conversion-gate02/75/Trees-26-2048.jpg)

![1.[Push NULL onto STACK and initialize PTR]
TOP1,STACK[1]NULL and PTRROOT
2.Repeat while PTR!=NULL [Push left most path onto
stack]
a)TOPTOP+1 and STACK[TOP]PTR [Saves
nodes]
b)PTRLEFT[PTR] [updates PTR]
[End of loop]
3.PTRSTACK[TOP]
TOPTOP-1 [pops node from STACK]](https://image.slidesharecdn.com/trees-141206172727-conversion-gate02/75/Trees-28-2048.jpg)
![4.Repeat steps 5 to 7 while PTR!=NULL [Backtracking]
5.Apply PROCESS to INFO[PTR]
6.[Right child?]
If RIGHT[PTR]!=NULL
a)PTRRIGHT[PTR]
b)GOTO step 2
7.PTRSTACK[TOP]
TOP=TOP-1 [Pops node]
[end of step 4 loop]
8.Exit](https://image.slidesharecdn.com/trees-141206172727-conversion-gate02/75/Trees-29-2048.jpg)

![1.[push NULL onto STACK and initialize PTR]
Set TOP1,STACK[1]NULL,PTRROOT
2.[Push left-most path onto STACK]
Repeat steps 3 to 5 while(PTR!=NULL)
3.TOPTOP+1
STACK[TOP]PTR [ Pushes PTR on STACK]
4.if RIGHT[PTR]!=NULL, then [Push on STACK]
TOPTOP+1 and STACK[TOP]=-RIGHT[PTR].
[end of If strucutre]](https://image.slidesharecdn.com/trees-141206172727-conversion-gate02/75/Trees-31-2048.jpg)
![Set PTRLEFT[PTR] [Updates pointer PTR]
[End of Step 2 loop]
6.Set PTRSTACK[TOP] and TOPTOP-1 [Pops node from
STACK]
7.Repeat while PTR>0.
A)Apply PROCESS to INFO[PTR]
B)Set PTRSTACK[TOP] and TOPTOP-1 [pops node
from STACK]
8.If PTR<0 ,then:
a)PTR-PTR
b)Goto step 2.
[End of If structure]
9.EXIT](https://image.slidesharecdn.com/trees-141206172727-conversion-gate02/75/Trees-32-2048.jpg)




![1. PTRROOT [Stores address of ROOT into PTR]
2. FLAG0 [Assume search is unsuccessful]
3. LOCNULL
4. Repeat steps while PTR!=NULL and FLAG=0
5. If ITEM =INFO(PTR) then [Item found]
FLAG1, LOCPTR
Else if ITEM < INFO(PTR) then [Item in left subtree]
PTRLEFT(PTR)
Else
PTRRIGHT(PTR) [Item in right subtree]
[End if structure]
[End of step 4 loop]](https://image.slidesharecdn.com/trees-141206172727-conversion-gate02/75/Trees-37-2048.jpg)



![1. If AVAIL=NULL then [No space for new node]
Write “ Overflow”.
return
[End of if structure]
2. [Get new node from availability list]
a) NEWAVIAL
b) AVAILLEFT(AVAIL)
c) INFO(NEW)ITEM [Copy ITEM into INFO part of new node]
3.[New node has no children]
a) LEFT(NEW)NULL
b) RIGHT(NEW)NULL
4.If ROOT=NULL then [Tree is empty]
ROOTNEW [Insert new node as root]
return
[End of if structure]](https://image.slidesharecdn.com/trees-141206172727-conversion-gate02/75/Trees-41-2048.jpg)
![[Remaining steps insert new node at appropriate location in non empty tree]
5.PTRROOT, PTRNULL
6. Repeat steps 7 and 8 while PTR!=NULL [Finding parent of new node]
7.PPTRPTR [ Make current node as parent]
8. If ITEM> INFO(PTR) then [Item>current node’s INFO part]
PTRRIGHT(PTR) [Move towards right subtree]
ELSE
PTRLEFT(PTR) [Move towards left subtree]
[End of If structure]
[End of step 6 loop]
9.If ITEM<INFO(PPTR) then
LEFT(PPTR)NEW [Insert new node as left child]
Else
RIGHT(PPTR)NEW [Insert new as right child]
10. Return](https://image.slidesharecdn.com/trees-141206172727-conversion-gate02/75/Trees-42-2048.jpg)

![1.PTRROOT, FLAG0 [Initialize PTR, assume search successful]
2. Repeat steps 3 while PTR!=NULL [All nodes served ] and FLAG=0 [Search
Unsuccessful]
3. If ITEM=INFO(PTR) then [Node to be deleted found]
FLAG1, LOCPTR
Else If ITEM < INFO(PTR) then [ITEM in left subtree]
PPTRPTR [Make current node as a parent]
PTRLEFT(PTR) [Make a left child as current node]
Else [ITEM in right subtree]
PPTRPTR
PTRRIGHT(PTR)
[End of If structure]
[End of step 3 loop]
4. If LOC=NULL then
Write “ITEM does not exist”
return](https://image.slidesharecdn.com/trees-141206172727-conversion-gate02/75/Trees-44-2048.jpg)
![[End of If structure]
5. If RIGHT(LOC)!=NULL and LEFT(LOC)!=NULL then [ Case 3]
Call DELNODE_TWOCH(ROOT, LOC, PPTR)
Else[Case 1 and Case 2]
Call DELNODE_ZRONECH(ROOT,LOC,PPTR)
[End of If structure]
6.[Returning deleted node to availability list]
LEFT(LOC)AVAIL
AVAILLOC
7. Return](https://image.slidesharecdn.com/trees-141206172727-conversion-gate02/75/Trees-45-2048.jpg)

![1.[Initialize childnode]
If LEFT(LOC)=NULL and RIGHT(LOC)=NULL then [No Child]
CHILDNODENULL
Else If LEFT(LOC)!=NULL then
CHILDNODELEFT(LOC)
Else
CHILDNODERIGHT(LOC)
[End of If structure]
2.If PPTR=NULL then [No parent]
ROOTCHILDNODE
Else If LOC=LEFT(PPTR) then [Deleted node to the left of parent node]
LEFT(PPTR)CHILDNODE
ELSE [Deleted Node to the right of parent node]
RIGHT(PPTR)CHILDNODE
[End of If structure] [End of structure] 3. Return](https://image.slidesharecdn.com/trees-141206172727-conversion-gate02/75/Trees-47-2048.jpg)

![[Find inorder successor node and parent of successor node[Step 1 and 2]]
1.SUCCRIGHT(LOC), PARSUCCLOC
2. Repeat while LEFT(SUCC) !=NULL
PARSUCCSUCC [ Make successor as parent]
SUCCLEFT(SUCC) [ Make left child of successor as successor node]
[End of Step 2 loop]
3. Call DELNODE_ZRONECH(ROOT,SUCC,PARSUCC) [Delete inorder successor]
[Steps 4 and 5 replace node N by its inorder successor]
4. If PARSUCC=NULL then [No Parent]
ROOTSUCC
Else if LOC=LEFT(PPTR) then [deleted node to left of its parent]
LEFT(PPTR)SUCC
Else [deleted node to right of its parent]
RIGHT(PPTR)SUCC](https://image.slidesharecdn.com/trees-141206172727-conversion-gate02/75/Trees-49-2048.jpg)
![[End of If structure]
5. a) LEFT(SUCC)LEFT(LOC)
b) RIGHT(SUCC)RIGHT(LOC)
6. Return](https://image.slidesharecdn.com/trees-141206172727-conversion-gate02/75/Trees-50-2048.jpg)