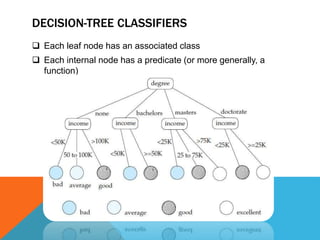
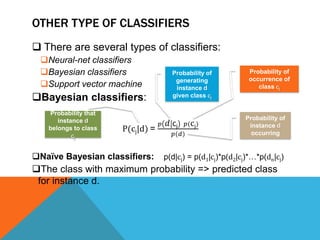
The document discusses various data mining and machine learning techniques. It describes data mining as the process of analyzing large databases to find useful patterns. It discusses classification, decision trees, regression, support vector machines, and validating classifiers. Classification involves predicting which class new data belongs to, based on attributes. Decision trees use a greedy algorithm to recursively split data into pure subsets. Regression predicts a numeric value. Support vector machines find the maximum margin separating hyperplane. Validating classifiers measures accuracy on test data.

2. DATA MINING
 The process of semiautomatically analyzing large
databases to find useful patterns.
 Knowledge discovered can be represented by:
 A set of rules (degree of support and confidance)
 Equations relating different variables to each other
 Other mechanisms for predicting outcomes
 Most widely used applications:
 Prediction: if the person is a good credit risk.
 Association: books that tend to be bought together.

3. CLASSIFICATION
 Given the items belong to one of several classes,
and given past instances (training instances) of
items along with the classes to which they belong,
the problem is to predict the class to which a new
item belongs.

4. CLASSIFICATION
 Classification can be done by finding rules that partition
the given data into disjoint groups.
 A case study: Credit-card company
 The company assigns a credit-worthiness level of:
excellent, good, average, bad to each of a sample
set of current customers.
 Then it attempts to find rules that classify its current
customers into those classes.

5. CLASSIFICATION
 For example:
∀person P, P.degree = masters and P.income > 75, 000 ⇒ P.credit = excellent
∀ person P, P.degree = bachelors or
(P.income ≥ 25, 000 and P.income ≤ 75, 000) ⇒ P.credit = good
The process of building a classifier starts from a sample of
data: training set
For each tuple in the training set, the class to which the tuple
belongs is already known.
There are several ways of building a classifier…

6. DECISION-TREE CLASSIFIERS
 Each leaf node has an associated class
 Each internal node has a predicate (or more generally, a
function)

7. BUILDING DECISION-TREE CLASSIFIERS
 The most common way: a greedy algorithm
 Works recursively, starting at the root with all training
instances associated, and building the three
downward.
 At each node, if all or almost all training instances
associated with it, belong to the same class => the
node becomes a leaf node associated with that class.
 Otherwise, a partitioning attribute and partitioning
condition must be selected to create child nodes.

8. BEST SPLITS
 To judge the benefit of picking a particular attribute
and condition for partitioning of the data at a node,
we measure the purity of the data at the children
resulting from partitioning by that attribute.
 The attribute and condition that result in the
maximum purity are chosen.
 The purity of a set S of training instances can be
measured in several ways…

9. BEST SPLITS

10. BEST SPLITS
 the information gain due to a particular split of S into Si:
Information-gain(S,{Si, Si,..., Si}) = purity(S) - purity(Si, Si,..., Si)
 The information content of a particular split can be
defined in terms of entropy as:
Information-content(S,{Si, Si,..., Si}) = - 𝑖−1
𝑟 |Si|
|𝑆|
log2
|Si|
|𝑆|
 The best split for an attribute is the one that gives the
maximum information gain ratio, defined as:
𝐼𝑛𝑓𝑜𝑟𝑚𝑎𝑡𝑖𝑜𝑛 − 𝑔𝑎𝑖𝑛(S,{Si, Si,..., Si})
𝐼𝑛𝑓𝑜𝑟𝑚𝑎𝑡𝑖𝑜𝑛 − 𝑐𝑜𝑛𝑡𝑒𝑛𝑡(S,{Si, Si,..., Si})

11. FINDING BEST SPLITS
 How to split an attribute depends on type of it.
Continuous values can be ordered, like numbers
(income)
Categorical values have no meaningful order (degree)
 Continuous-valued attribute, finding best binary splits :
First sort the attribute values in the training instances.
Then compute the information gain obtained by splitting
at each value. (training instance values: 1,10,15,25 => split
points: 1,10,15)
 For a categorical attribute, a child for each value.

12. DECISION-TREE CONSTRUCTION ALGORITHM
 Evaluate different attributes and different
partitioning conditions, and pick the one that results
in maximum information-gain ratio.
 The same procedure works recursively on each of
the sets resulting from the split.
 The recursion stops when the purity of a set is 0 or
sufficiently high.

13. DECISION-TREE CONSTRUCTION ALGORITHM
procedure GrowTree(S)
Partition(S);
procedure Partition (S)
if (purity(S) > p or |S| < s ) then
return;
for each attribute A
evaluate splits on attribute A;
Use best split found (across all attributes) to partition
S into S1, S2, . . . , Sr ;
for i = 1, 2, . . . , r
Partition(Si );
For each leaf node we generate a rule as follows:
Degree=masters and income>75000 => excellent
conjunction of all the split conditions on the path to the leaf class of the leaf

14. OTHER TYPE OF CLASSIFIERS
 There are several types of classifiers:
Neural-net classifiers
Bayesian classifiers
Support vector machine
Bayesian classifiers:
P(cj|d) =
𝑝 𝑑 cj 𝑝(cj)
𝑝(𝑑)
Naïve Bayesian classifiers: p(d|cj) = p(d1|cj)*p(d2|cj)*…*p(dn|cj)
The class with maximum probability => predicted class
for instance d.
Probability of
occurrence of
class cj
Probability of
generating
instance d
given class cj
Probability of
instance d
occurring
Probability that
instance d
belongs to class
cj

15. THE SUPPORT VECTOR MACHINE (SVM)
 We are given a training set of points whose class is known.
 We need to build a classifier of points using these training
points.
 Suppose a line, such that all points in class A lie to one side and
all points in class B lie to the other.
 The SVM classifier chooses the line whose distance from the
nearest point in either class is maximum: the maximum
margin line
X: points in class
A
O: points in class
B

16. REGRESSION
 Deals with the prediction of a value, rather than a class.
 Given values for a set variables, X1,X2,…,Xn, we wish to
predicate the value of the variable Y.
 Linear regression:
Y = a0 + a1*X1 + a2*X2 + … an*Xn
 Curve fitting (may be only approximate)
 Regression aims to find coefficients that gives the best
possible fit.

17. VALIDATING A CLASSIFIER
 Measuring its classification error, before deciding to use it.
 A set of test cases where the outcome is already known is used.
 The quality of classifier can be measured in several ways:
1. Accuracy: (t-pos+t-neg)/(pos+neg)
2. Recall (Sensitivity): t-pos/pos
3. Precision: t-pos/(t-pos+f-pos)
4. Specificity: t-neg/neg
Which of these should be used, depends on the needs of
application.
It’s a bad idea to use exactly the same set of test cases to train as
well as to measure the quality of classifier.