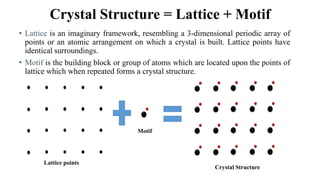
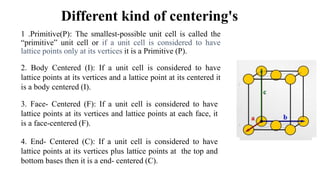
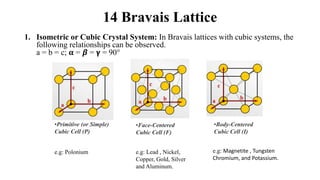
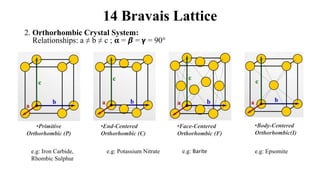
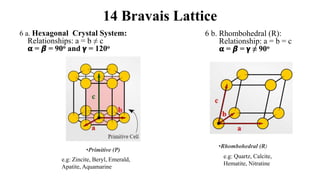
The document discusses Bravais lattices, which are the 14 possible arrangements of points in a crystal structure that satisfy translational symmetry. A Bravais lattice is composed of a motif that is repeated by translations to form the crystal structure. There are six crystal systems that the 14 Bravais lattices fall into based on their unit cell dimensions and angles. The document provides examples of common crystal structures that use each of the different Bravais lattice types.

1. Bravais Lattice
Sujan Raj Pandey/ 05
M.Sc. 1st Semester, 2077

2. Crystal Structure = Lattice + Motif
• Lattice is an imaginary framework, resembling a 3-dimensional periodic array of
points or an atomic arrangement on which a crystal is built. Lattice points have
identical surroundings.
• Motif is the building block or group of atoms which are located upon the points of
lattice which when repeated forms a crystal structure.
Lattice points
Motif
Crystal Structure

3. Bravais Law
• Crystal faces develop along planes defined by the points in the lattice. In other
words, all crystal faces must intersect atoms or molecules that make up the points.
• In 1850, Auguste Bravais found that, “ A face is more commonly developed in a
crystal if it intersects a larger number of lattice points.” This is known as the
Bravais Law.
• In general, the line that connects most of the lattice points decides the faces.
• For example, in the plane lattice shown at the
right, faces will be more common if they
develop along the lattice planes labeled 1,
somewhat common if they develop along those
labeled 2, and less and less common if they
develop along planes labeled 3, 4, and 5.

4. Bravais Lattice
• Bravais lattices are the foundation for crystal structures
• Bravais lattices move a specific motif by translation symmetry so that it lines up to
an identical motif and divides the lattice into number of identical blocks or unit cell.
• In 1850,Bravais showed that identical points can be arranged spatially to produce
14 types of unit cell.
• Thus, a Bravais lattice refer that only these 14 types of unit cells are compatible
with the orderly arrangements of atoms found in crystals.
• The 14 Bravais lattice are distributed within the six crystal system with each crystal
system having four different types of centering.

5. Different kind of centering's
1 .Primitive(P): The smallest-possible unit cell is called the
“primitive” unit cell or if a unit cell is considered to have
lattice points only at its vertices it is a Primitive (P).
2. Body Centered (I): If a unit cell is considered to have
lattice points at its vertices and a lattice point at its centered it
is a body centered (I).
3. Face- Centered (F): If a unit cell is considered to have
lattice points at its vertices and lattice points at each face, it
is a face-centered (F).
4. End- Centered (C): If a unit cell is considered to have
lattice points at its vertices plus lattice points at the top and
bottom bases then it is a end- centered (C).

6. 14 Bravais Lattice
1. Isometric or Cubic Crystal System: In Bravais lattices with cubic systems, the
following relationships can be observed.
a = b = c; 𝛂 = 𝞫 = 𝝲 = 90°
•Primitive (or Simple)
Cubic Cell (P)
•Face-Centered
Cubic Cell (F)
•Body-Centered
Cubic Cell (I)
e.g: Polonium e.g: Lead , Nickel,
Copper, Gold, Silver
and Aluminum.
e.g: Magnetite , Tungsten
Chromium, and Potassium.

7. 14 Bravais Lattice
2. Orthorhombic Crystal System:
Relationships: a ≠ b ≠ c ; 𝛂 = 𝞫 = 𝝲 = 90°
•Primitive
Orthorhombic (P)
•Face-Centered
Orthorhombic (F)
•Body-Centered
Orthorhombic(I)
•End-Centered
Orthorhombic (C)
e.g: Iron Carbide,
Rhombic Sulphur
e.g: Potassium Nitrate e.g: Barite e.g: Epsomite

8. 14 Bravais Lattice
3. Tetragonal Crystal System:
Relationships: a = b ≠ c ; 𝛂 = 𝞫 = 𝝲 = 90°
•Primitive
Tetragonal (P)
•Body-Centered
Tetragonal (I)
e.g: Cassiterite e.g:Rutile

9. 14 Bravais Lattice
4. Monoclinic Crystal System:
Relationships: a ≠ b ≠ c;
𝞫 = 𝝲 = 90o and 𝛂 ≠ 90o
•Primitive
Monoclinic (P)
•End-Centered
Monoclinic (C)
5. Triclinic Crystal System:
Relationships: a ≠ b ≠ c;
𝛂 ≠ 𝞫 ≠ 𝝲 ≠ 90o
•Primitive Triclinic
(P)
e.g: 𝞫- Sulphur,
Nickel Titanium
e.g: Tenorite,
sodium sulfate
e.g: Plagioclase,
Microcline, Kyanite

10. 14 Bravais Lattice
6 a. Hexagonal Crystal System:
Relationships: a = b ≠ c
𝛂 = 𝞫 = 90o and 𝝲 = 120o
•Primitive (P)
6 b. Rhombohedral (R):
Relationship: a = b = c
𝛂 = 𝞫 = 𝝲 ≠ 90o
•Rhombohedral (R)
e.g: Quartz, Calcite,
Hematite, Nitratine
e.g: Zincite, Beryl, Emerald,
Apatite, Aquamarine