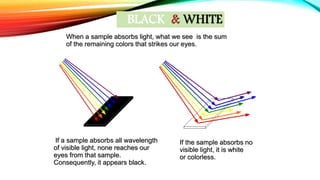
Crystal Field Theory (CFT) explains the color properties and magnetic characteristics of transition metal complexes by describing the bonding between ligands and metals through the splitting of d-orbitals in the presence of ligands. The striking colors of these complexes result from d-d electronic transitions, where electrons jump between split d-orbitals when excited by photons. However, CFT has limitations, including its inability to account for orbital splitting beyond d-orbitals and the order of ligands in the spectro-chemical series.

1. CRYSTAL FIELD THEORY
Colour Properties

2. TRANSITION ELEMENTS
• Present in abundance in the periodic table
• f-block elements
• d-block elements

3. COORDINATION COMPLEXES
𝑴

4. MAGNETIC & COLOUR PROPERTIES

6. WHY CFT???
 Werner’s Theory
 Valence Bond Theory
COULD NOT
EXPLAIN THE
COLOUR
PROPERTIES

7. Introduction To CFT
• Proposed by Bethe and van Vleck.
• Orgel used the concept of crystal field theory to define nature of
bonding between ligands and metals.
• It defines the bonding in ionic crystals due to which
this theory is known as crystal field theory.

8. • Crystal field theory (CFT) explains many important properties of
transition-metal complexes, including their
ocolours,
omagnetism,
ostructures,
ostability, and
oreactivity

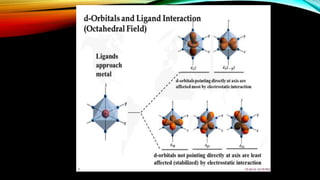
10. • d-orbitals are degenerate
• BUT, when ligands get
attached and are uniformly
distributed; their energy gets
higher
• IF, the ligands are oriented at
the axes i.e. x, y and z, the
degeneracy gets removed and
the d-orbitals split into two
groups [ 𝐞 𝒈 & 𝐭2𝑔]

11. • the 𝐞 𝐠 group consists of
𝐝 𝑧
2 & d𝜘2 𝑦2 , these have
electrons ON the x, y
and z axis
• while, the t2g has dxy,
dyz dzx having electrons
in BETWEEN the xy, yz
and zx axes
• the energies of these two
groups 𝐞 𝐠 & t2g depend
on their orientations in
space

13. APPEARANCE OF COLOURS
• The striking colours that these metal complexes show are because
of the d-d transition of electrons in the d-orbitals
• Involves the jumping of electrons from lower energy orbitals and
their subsequent jumping back
• Jumping occurs when electrons get excited
• In case of colour properties, excitation is caused by photons of
visible light
• A photon of light can excite and can cause jumping, if its energy is
equal to the crystal field splitting energy (Δo) (CFSE)
• CFSE is the difference in energy between the two sets of d-orbitals
• Energy is absorbed and then released, respectively

15. COLORS & HOW WE
PERCEIVE IT
800
430
650 580
560
490
Artist color wheel
showing the colors which
are complementary to one
another and the wavelength
range of each color.
400

16. BLACK & WHITE
If a sample absorbs all wavelength
of visible light, none reaches our
eyes from that sample.
Consequently, it appears black.
When a sample absorbs light, what we see is the sum
of the remaining colors that strikes our eyes.
If the sample absorbs no
visible light, it is white
or colorless.

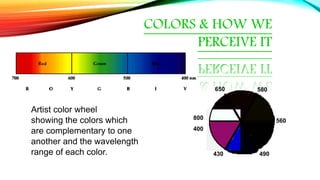
17. COMPLEX INFLUENCE ON
COLOR
[Fe(H2O)6]3+
[Co(H2O)6]2+
[Ni(H2O)6]2+
[Cu(H2O)6]2+
[Zn(H2O)6]2+
800
430
650 580
560
490
400

18. Gemstone owe their color from trace
transition-metal ions
Corundum mineral, Al2O3: Colorless
Cr → Al : Ruby
Mn → Al : Amethyst
Fe → Al : Topaz
TRANSITITON METAL GEMS

19. Ti & Co Al: Sapphire
Beryl mineral, Be3 Al 2Si6O18: Colorless
Cr → Al : Emerald
Fe → Al : Aquamarine

20. LIMITATIONS OF CFT
1. This theory does not consider the splitting of the orbital other than d
orbital.
2. The order of ligand in the Spectro-chemical series can not be
explained solely on electrostatic ground.

21. THANK YOU!!! 