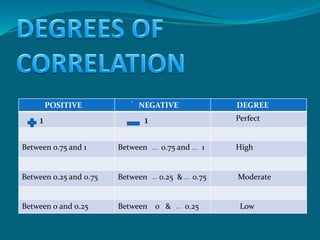
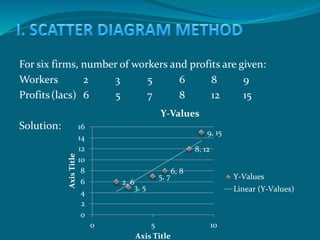
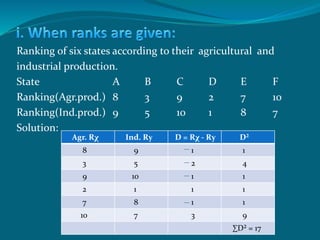
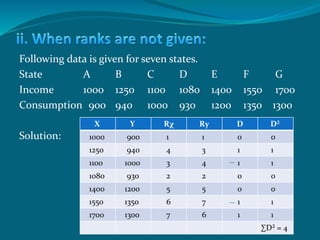
The document discusses correlation as a statistical method to analyze the relationship between variables, detailing positive and negative correlations as well as their degrees. It includes various methods for calculating correlation, such as the scatter diagram and rank methods, along with practical examples and calculations for different datasets. Additionally, it outlines the significance of correlation coefficients in understanding the extent of relationships between variables.

1. Rajat Sharma

2. Correlation is a statistical technique with the
help of which we study the extent, nature and
significance of association between the given
variables.
Thus in correlation we study:
 The given variables are associated or not
 What is the extent of association
 Whether variables are associated positively
or negatively

3.  Correlation is an analysis of the covariance
between two or more variables.
By A.M. Tuttle
 Correlation deals with the association
between two or more variables.
By Simpson
 Correlation shows us the degree to which
variables are linearly related.
By Wonnacott

4. 1) Positive Correlation. If direction of
change in two variables is same,
correlation is said to be positive.
X Y
X Y
For eg; income and consumption

5. 2) Negative Correlation. If direction of
change in the two variables is different ,
correlation is said to be negative.
X Y
X Y
For eg; demand and price

6. POSITIVE NEGATIVE DEGREE
1 1 Perfect
Between 0.75 and 1 Between 0.75 and 1 High
Between 0.25 and 0.75 Between 0.25 & 0.75 Moderate
Between 0 and 0.25 Between 0 & 0.25 Low
.
.
.
.
.
.

7. I. Scatter Diagram Method.
II. Karl Pearson’s Method.
III. Spearmen’s Rank Method.
IV. Concurrent Deviation Method.

8. For six firms, number of workers and profits are given:
Workers 2 3 5 6 8 9
Profits(lacs) 6 5 7 8 12 15
Solution:
2, 6
3, 5
5, 7
6, 8
8, 12
9, 15
0
2
4
6
8
10
12
14
16
0 5 10
AxisTitle
Axis Title
Y-Values
Y-Values
Linear (Y-Values)

9. Find the correlation between age of a child and his weight.
Age(years) 1 2 3 4 5
Weight(kgs.) 3 4 6 7 10
Solution:
X Y X² Y² XY
1 3 1 9 3
2 4 4 16 8
3 6 9 36 18
4 7 16 49 28
5 10 25 100 50
∑X = 15 ∑Y = 30 ∑X² = 55 ∑Y² = 210 ∑XY = 107

10. rχу = n∑XY - ∑X ∑Y
√n∑X² - (∑X)² √n∑Y² - (∑Y)²
rχу = (5) (107) – (15) (30)
√(5) (55) – (5)² √(5) (210) – (30)²
rχу = 535 – 450
√275 – 225 √1050 – 900
rχу = 85 = 85 rχу = 0.981
√7500 86.6

11. There are three types of problems in rank
method:
i. When ranks are given.
ii. When ranks are not given.
iii. When ranks repeat.

12. Ranking of six states according to their agricultural and
industrial production.
State A B C D E F
Ranking(Agr.prod.) 8 3 9 2 7 10
Ranking(Ind.prod.) 9 5 10 1 8 7
Solution:
Agr. Rχ Ind. Rу D = Rχ - Rу D²
8 9 1 1
3 5 2 4
9 10 1 1
2 1 1 1
7 8 1 1
10 7 3 9
∑D² = 17

13. rѕ = 1 – 6∑D²
n³ - n
rs = 1 – (6) (17)
6³ - 6
rs = 1 – 102 1 – 0.485
210
rs = 0.515

14. Following data is given for seven states.
State A B C D E F G
Income 1000 1250 1100 1080 1400 1550 1700
Consumption 900 940 1000 930 1200 1350 1300
Solution:
X Y Rχ Rу D D²
1000 900 1 1 0 0
1250 940 4 3 1 1
1100 1000 3 4 1 1
1080 930 2 2 0 0
1400 1200 5 5 0 0
1550 1350 6 7 1 1
1700 1300 7 6 1 1
∑D² = 4

15. rs = 1 – 6∑D²
n³ - n
rs = 1 – (6) (4)
7³ - 7
rs = 1 – 24
336
rs = 1 – 0.071
rs = 0.929

16. Following are the figures for fertilizers and output.
Fertilizer (kg) 35 40 25 55 85 90 65 55 45 50
Output(kg) 10 10 11 14 15 13 10 12 14 11
Solution:
X Y Rχ Rу D D²
35 10 2 2 0 0
40 10 3 2 1 1
25 11 1 4.5 3.5 12.25
55 14 6.5 8.5 2 4
85 15 9 10 1 1
90 13 10 7 3 9
65 10 8 2 6 36
55 12 6.5 6 0.5 0.25
45 14 4 8.5 4.5 20.25
50 11 5 4.5 0.5 0.25
∑D²=84

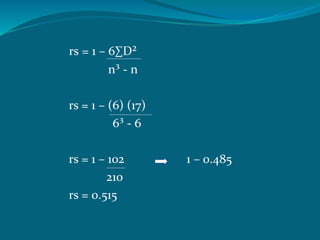
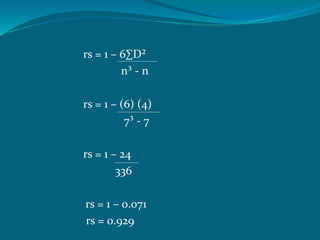
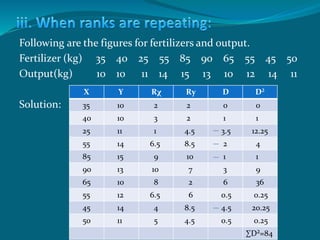
17. rs = 1 – 6[∑D² + 1/12 (m³ - m) + 1/12 (m³ - m) +.....]
n³ - n
rs = 1 – 6[84 + 1/12 (2³-2) + 1/12 (3³-3) + 1/12 (2³-2) + 1/12 (2³-2)
10³ - 10
rs = 1 – 6[84 + 6/12 + 24/12 + 6/12 + 6/12]
990
rs = 1 – 6[84 + 0.5 + 2 + 0.5 + 0.5]
990
rs = 1 – 525
990
rs = 0.47

18. Marks in Economics and Statistics are given below.
Economics 62 65 68 61 76 57 40 52
Statistics 75 79 82 85 90 68 48 50
Solution:
X Y Deviation X Deviation Y Concurrent Dev.
62 75 ...... ...... ......
65 79 + + + (c)
68 82 + + + (c)
61 85 - + ―
76 90 + + + (c)
57 68 - - + (c)
40 48 - - + (c)
52 50 + + + (c)
n = 7 C = 6

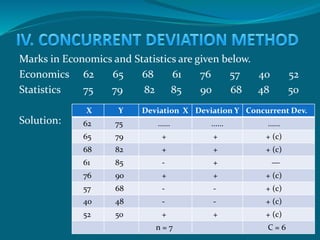
19. r = ±√ ±[2C – n]
√ n
r = ±√±[ (2) (6) – (7)]
√ 7
r = ±√± 0.714
r = 0.845