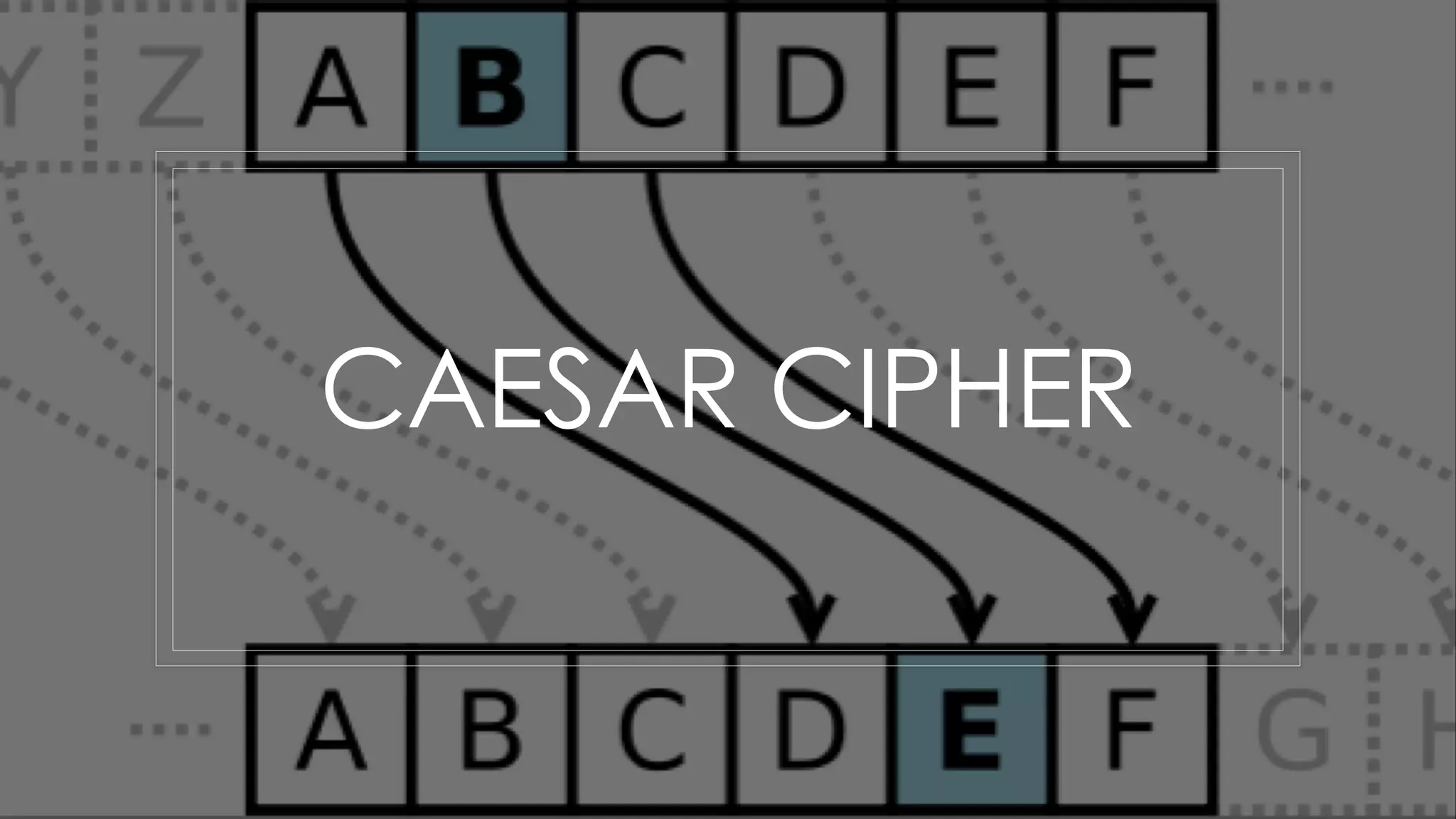
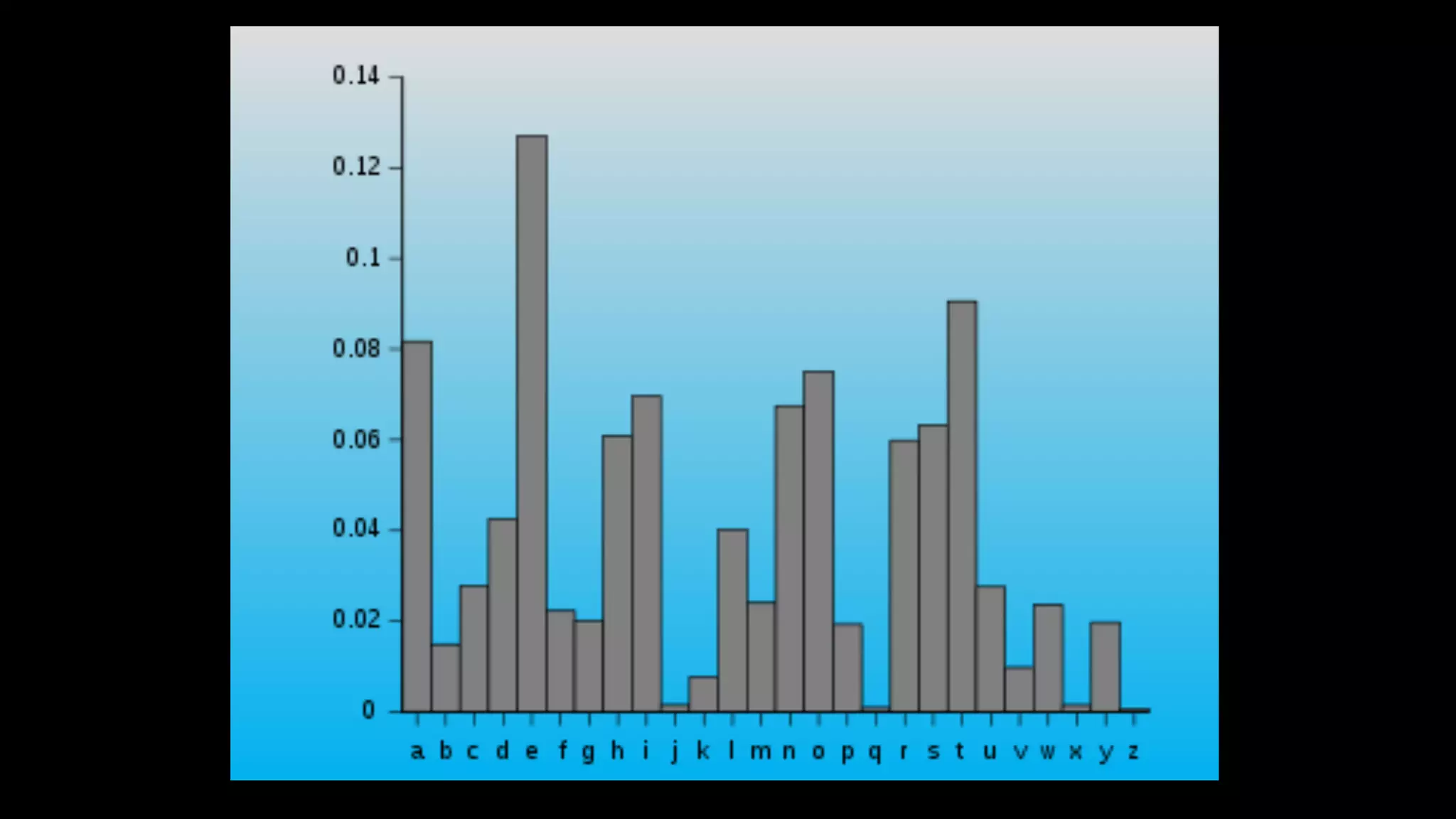
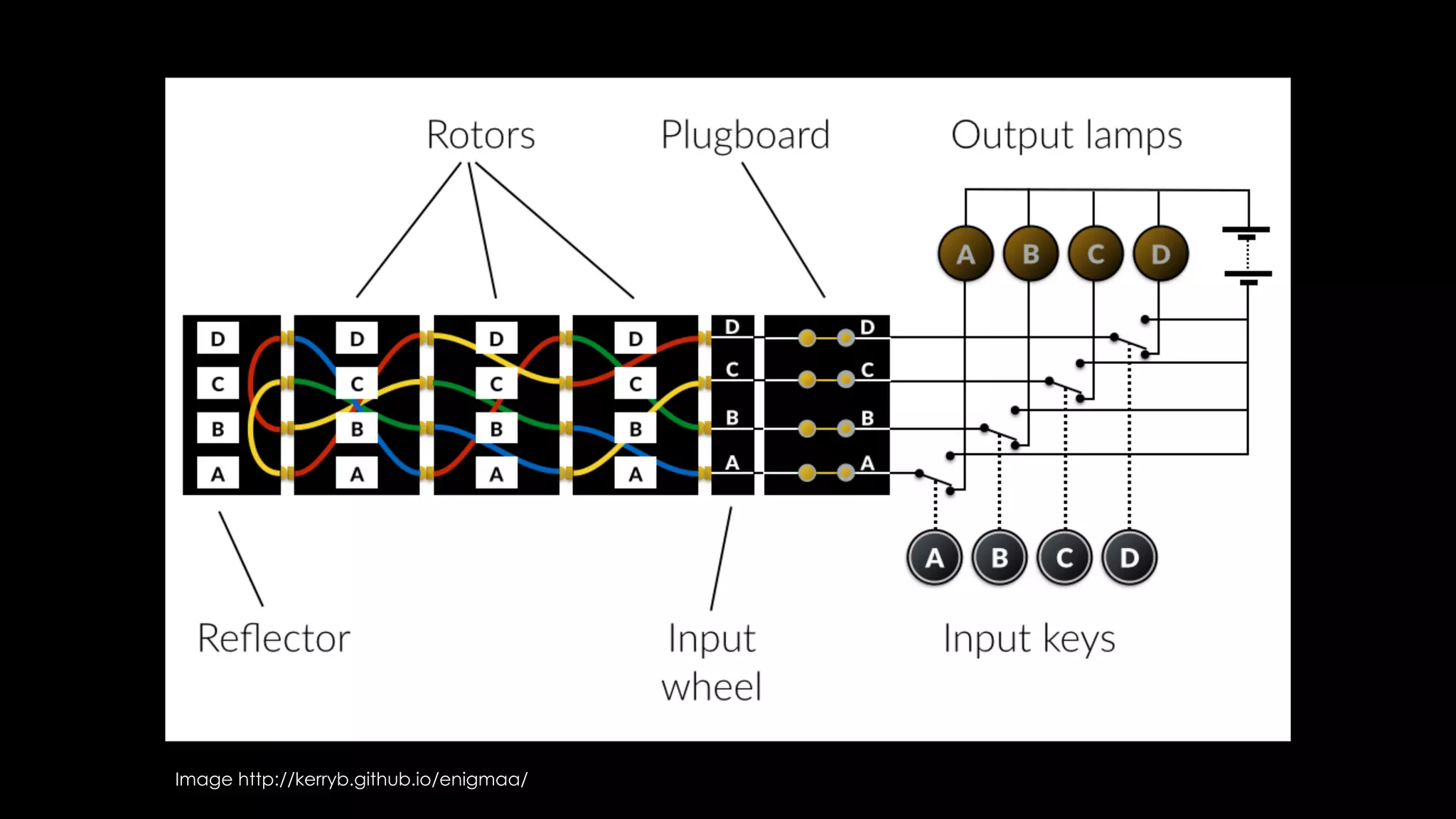
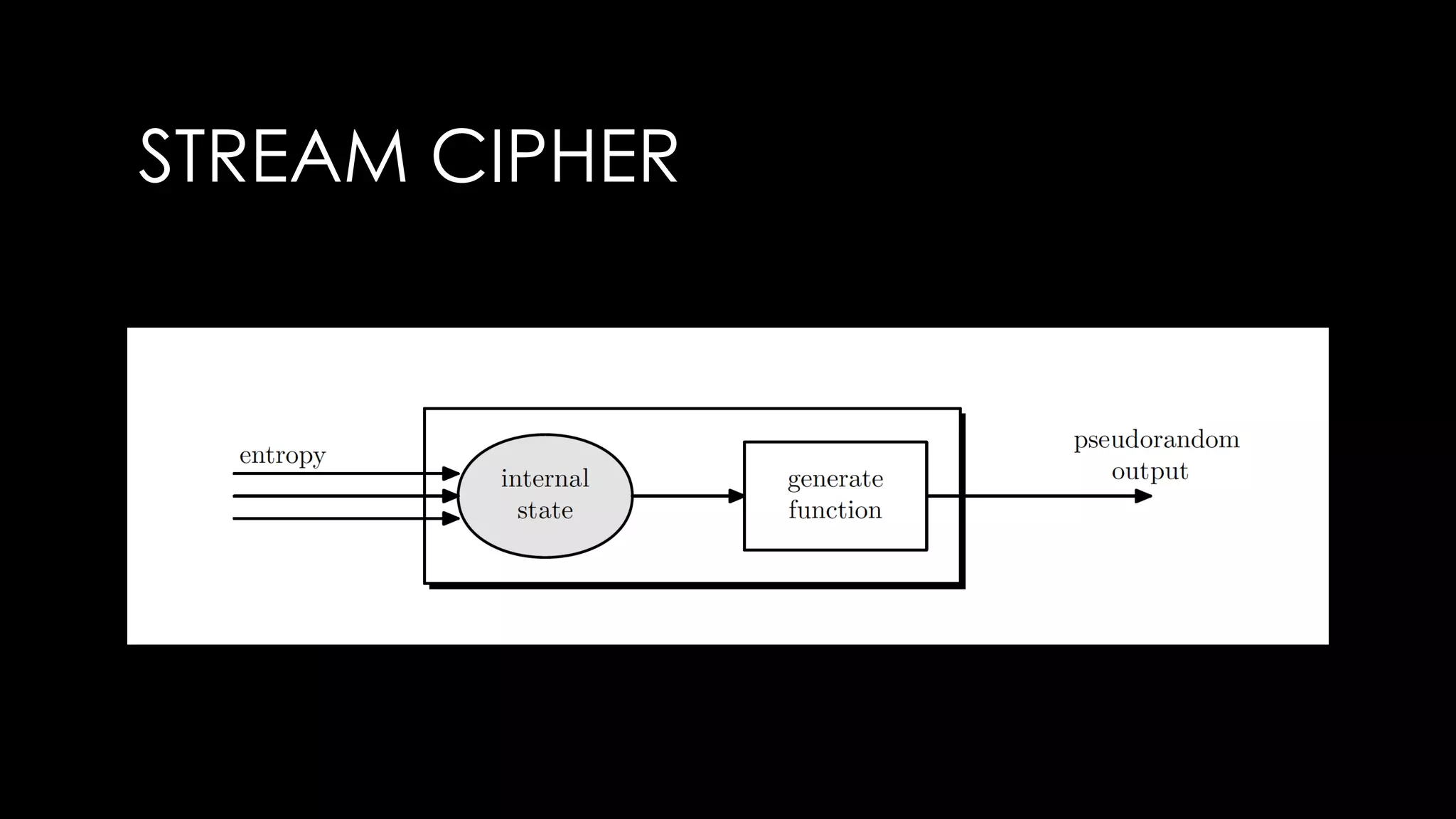
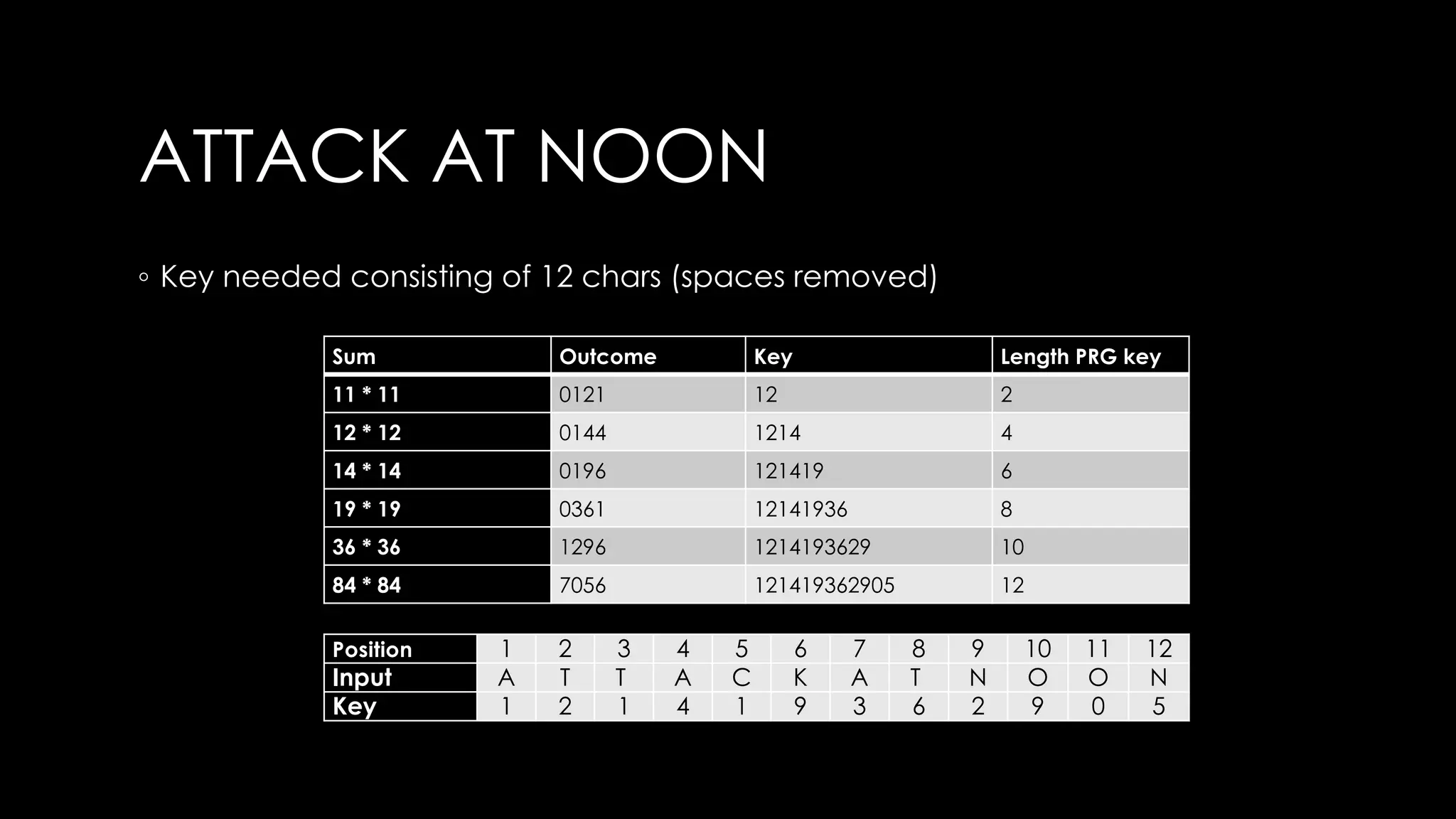
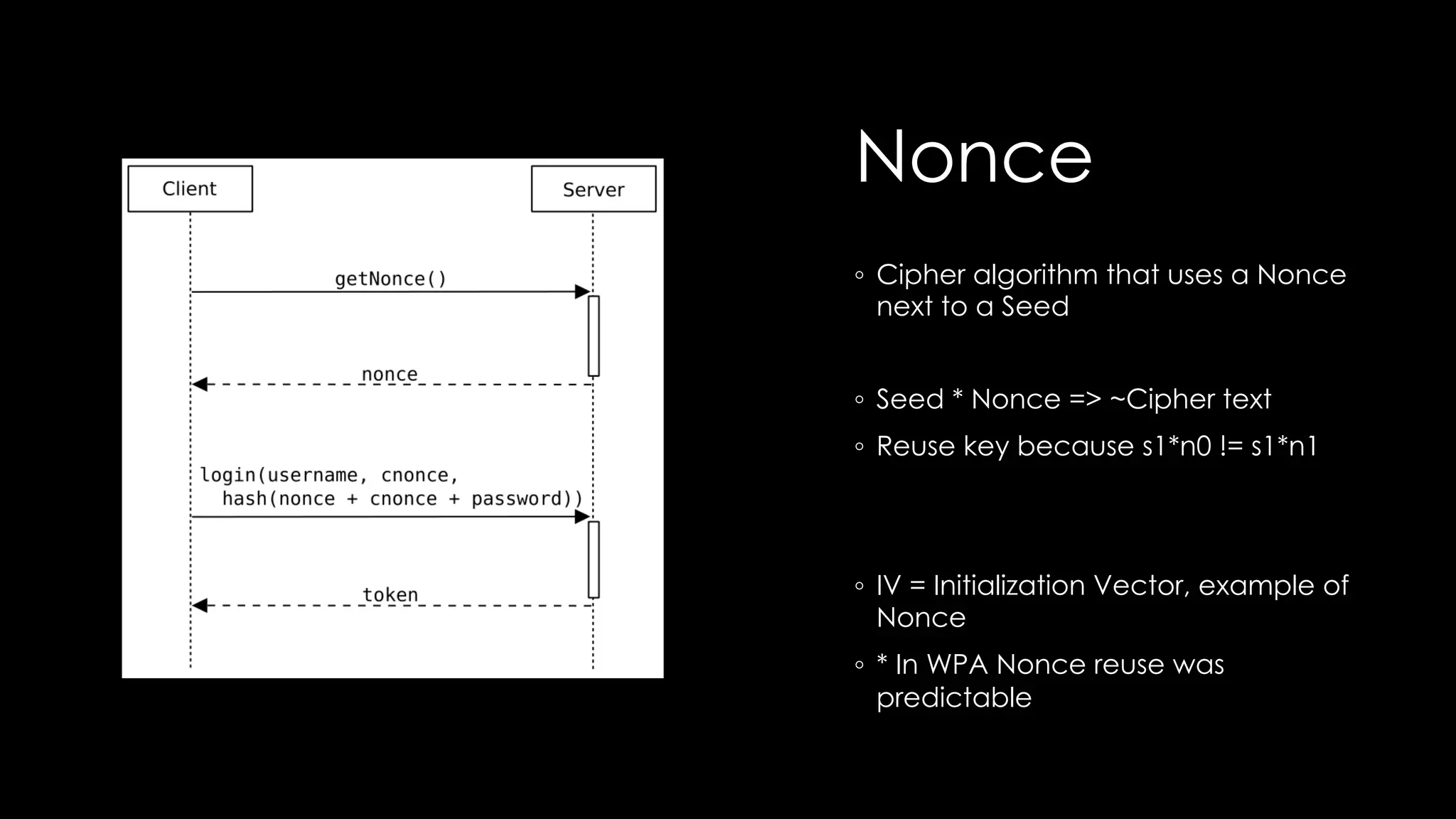
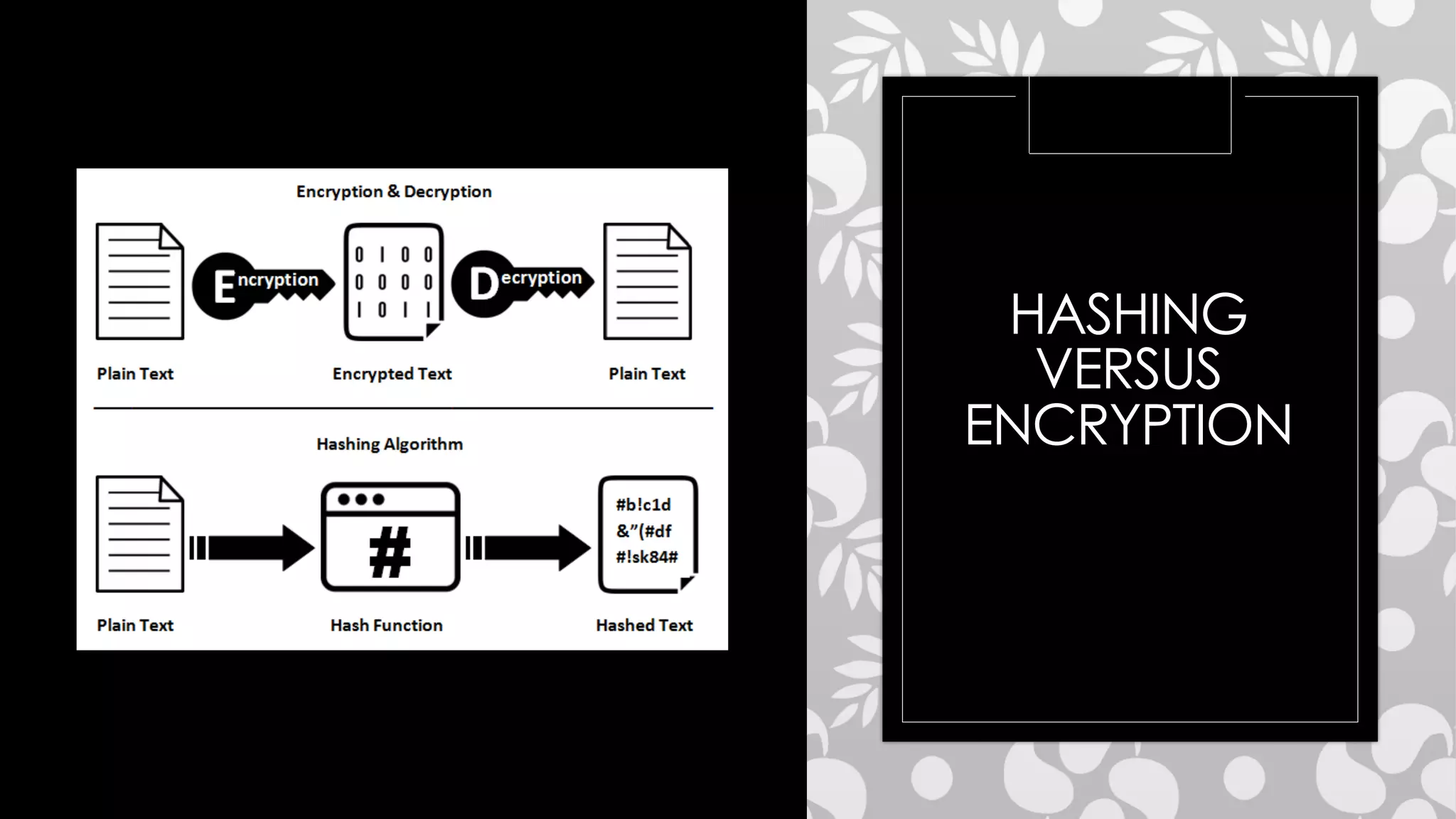
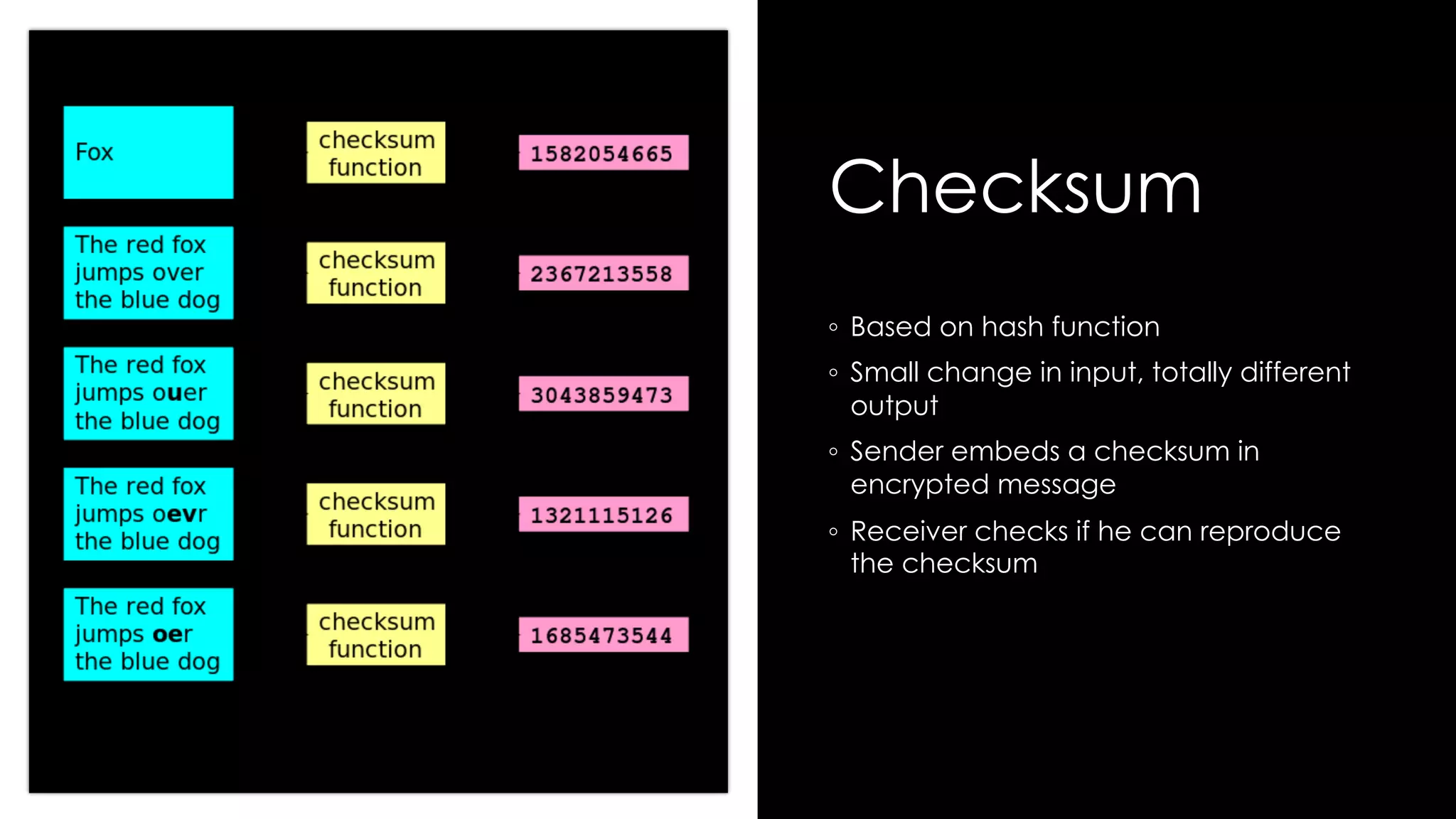
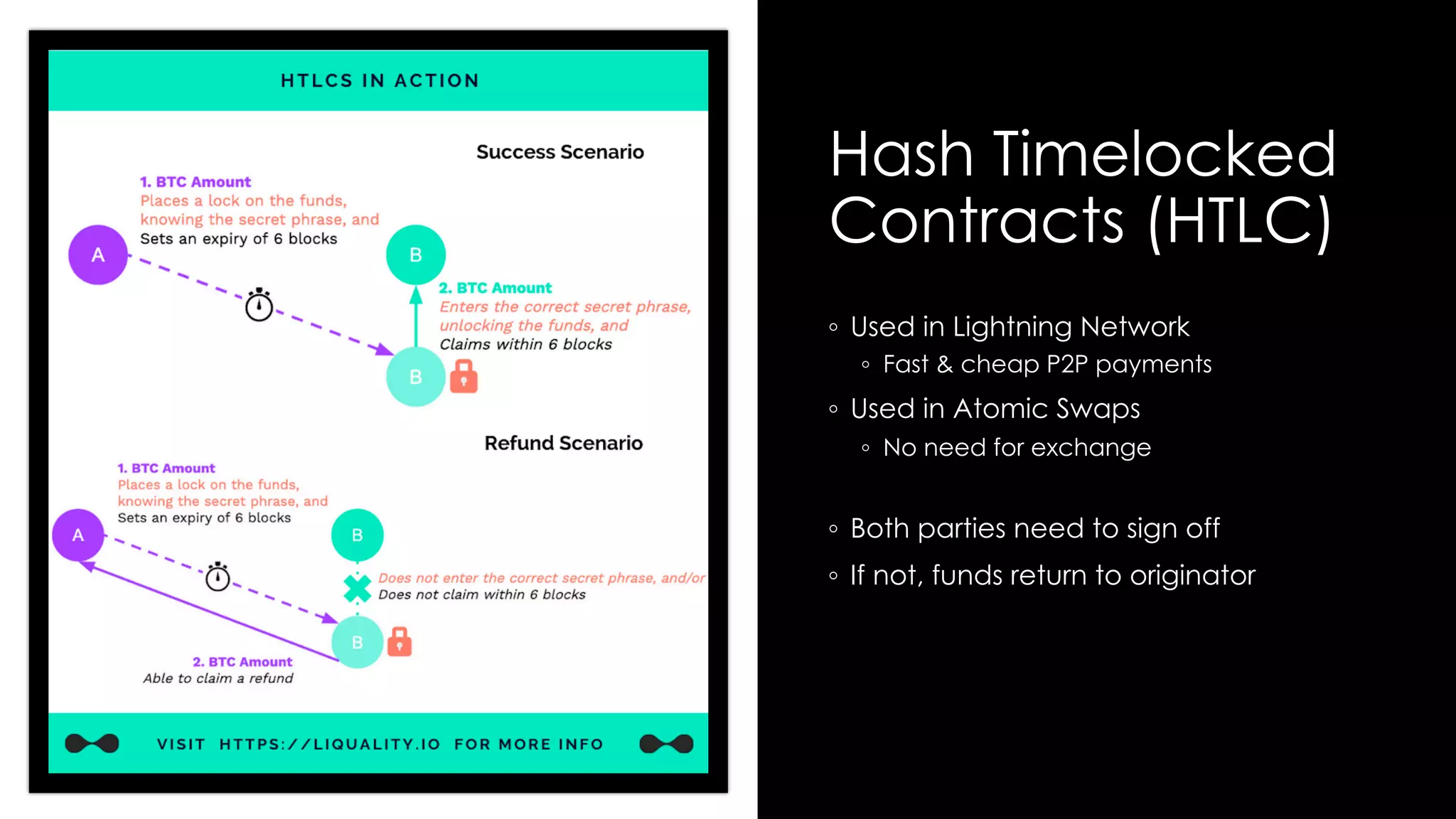
Roy Wasse presented an overview of cryptography concepts including classical ciphers like the Caesar cipher and Vigenère cipher. Modern symmetric ciphers use pseudorandom number generators with nonces to prevent key reuse. Asymmetric encryption allows public/private key pairs. Quantum computing may break current algorithms like RSA and ECC. Anonymity can be achieved using mixing services and onion routing. Zero-knowledge proofs allow verification without revealing information. New developments like Schnorr signatures and Mimblewimble aim to improve scalability and privacy in cryptocurrencies.

2. Intro
◦ Roy Wasse
◦ Co Founder OpenValue
◦ Dutch JUG leader
◦ Love technochange
◦ Disclaimer: no heavy math

3. ΚΡΥΠΤΕΙ
ΓΡΑΦΩ

4. CAESAR CIPHER

7. ◦ Invented by Leon Battista in 1467
◦ Uses multiple alphabets (polyalphabetic)
◦ Circumvents frequency analysis
A T T A C K A T D A W N
L E M O N L E M O N L E
L X F O P V E F R N H R
Vigenère cipher

8. Repetition is deadly

10. Playfair
◦ Key PLAYFAIR EXAMPLE
◦ Plaintext HI DE TH EG OL DI NT HE TR EX ES TU MP
◦ Ciphertext BM OD ZB XD NA BE KU DM UI XM MO UV IF

12. Image http://kerryb.github.io/enigmaa/

13. tps://hackaday.com/2016/04/29/centennial-birthday-of-claude-e-shannon-the-math-and-ee-
pioneer/

14. One time pad
◦ If and only if:
◦ Key length >= Source text
◦ Key is generated randomly
◦ Any key is used only once
◦ Only sender and receiver have key

15. One time function
Source T H I S I S S E C R E T
Position 20 8 9 19 9 19 19 5 3 18 5 20
KEY X V H E U W N O P G D L
+ 23 21 7 4 20 22 13 14 15 6 3 12
Result 43 29 16 23 29 41 32 19 18 24 8 32
Mod 26 17 3 16 23 3 15 6 19 18 24 8 6
Ciphertext R D Q X D P G T S Y 9 G

17. Disadvantages
One time pad
Works fine in some use
cases (pen & paper)
1 GB file requires 1 GB
random key
No access to true
random input
Key can only be used
once

18. Semantic
security
Shorter key
Pseudo random generator
Ciphers for varying message
length
Safe enough for vast amount of
computing power
Practical encryption !=
Mathematical safe

19. STREAM CIPHER

20. Middle Squares
method
◦ Take random input number (11)
◦ Square number (11 * 11 = 121)
◦ Select # middle chars (0121)
◦ add trailing zero if needed
◦ Square those (12 * 12 = 144)
◦ Repeat until key is long enough

21. ATTACK AT NOON
◦ Key needed consisting of 12 chars (spaces removed)
Sum Outcome Key Length PRG key
11 * 11 0121 12 2
12 * 12 0144 1214 4
14 * 14 0196 121419 6
19 * 19 0361 12141936 8
36 * 36 1296 1214193629 10
84 * 84 7056 121419362905 12
Position 1 2 3 4 5 6 7 8 9 10 11 12
Input A T T A C K A T N O O N
Key 1 2 1 4 1 9 3 6 2 9 0 5

22. Pseudo Random is hard

23. Nonce
◦ Cipher algorithm that uses a Nonce
next to a Seed
◦ Seed * Nonce => ~Cipher text
◦ Reuse key because s1*n0 != s1*n1
◦ IV = Initialization Vector, example of
Nonce
◦ * In WPA Nonce reuse was
predictable

24. C M V H
F R O M M O L L Y
Position 6 18 15 13 13 15 12 12 25
KEY X V H U W N O P G
+ 23 21 7 20 22 13 14 15 6
Result 29 39 22 33 35 28 26 27 31
Mod 26 3 13 22 7 9 2 0 1 5
Ciphertext C M V H J C A B X
F R O M A L I C E
Position 6 18 15 13 1 12 9 3 5
KEY D B J E L L M W A
+ 4 2 10 13 1 12 9 3 5
Result 10 20 25 26 2 24 18 6 10
Mod 26 10 20 25 0 2 24 18 6 10
Ciphertext K U Z A C Y S G K
C Y S G KK U Z A
J C A B X

25. HASHING
VERSUS
ENCRYPTION

26. Checksum
◦ Based on hash function
◦ Small change in input, totally different
output
◦ Sender embeds a checksum in
encrypted message
◦ Receiver checks if he can reproduce
the checksum

27. Block ciphers
Plaintext A B C D E F
Ciphertext F A B C D E
Ciphertext E F A C
Plaintext F A C E

29. Asymmetric encryption

31. Quantum computing
◦ Sohr‘s algorithm mid 90’s showed RSA is vulnerable
◦ ECC even more vulnerable
◦ To guess Private key in reasonable amount of time few thousand qubits needed
◦ Currently best Quantum computer has 20-50 qubits
◦ Supersingular Isogeny Diffie-Hellman is post-quantum secure

33. Mixing service & Onion Routing
◦ Implemented in TOR (The Onion Router)
◦ Alice want to send message to Bob’s forum anonymously
◦ Use proxy Carol ( A -> C -> B )
◦ Share a key with Carol and send cyphertext
◦ Use mixing service

34. Peeling the onion
◦ Use Multiple mixing services: David & Carol
◦ Encrypt message with key shared with David, then with key shared with Carol
◦ Carol doesn’t know she’s the entry point / Alice is a sender

35. Hash Timelocked
Contracts (HTLC)
◦ Used in Lightning Network
◦ Fast & cheap P2P payments
◦ Used in Atomic Swaps
◦ No need for exchange
◦ Both parties need to sign off
◦ If not, funds return to originator

36. Alice exchanges 1 BTC for 10 LTC with Bob
1. Create hash from key = BTC contract address
2. Deposit 1 BTC, require key and valid signature, with timelock
3. Send hash to Bob
1. Create same type of LTC contract address from hash
2. Deposit 10 LTC in contract
1. Collect LTC: Present valid signature to LTC contract and present key
2. Contract shares this key with Bob
1. Collect BTC: Present valid signature and
key to BTC contract

37. Commitment Scheme
◦ Alice & Bob going on a date, but which movie to pick?
◦ Coin flip can be manipulated
◦ Bob make a choice (bit commitment), send to Alice
◦ Coin is flipped, outcome is known to Alice & Bob
◦ Alice can now open envelope

38. Zero knowledge proof
CC BY 2.5, https://commons.wikimedia.org/w/index.php?curid=313648

39. ◦Sender’s address
◦Amount of coins sent
◦Receiver’s address

40. Exploiting multiplication to hide
information and verify ownership
Credit: https://medium.com/beam-mw/mimblewimble-explained-like-youre-12-d779a5bb483d

41. Hiding transaction amounts

42. Proving that money in = out

43. Schnorr Signatures
◦ Bitcoin uses script which signs several tx inputs for a
single tx
◦ Signatures take up a lot of space.
◦ Schnorr allows aggregating signatures like:
◦ Input A = Sig 10000
◦ Input B= Sig 5000
◦ Just store 15000 (10000+5000)
◦ This enables scriptless transactions, taproot and
submarine swaps
Image: https://bitcoinmagazine.com/articles/scriptless-scripts-how-bitcoin-can-support-smart-contracts-without-smart-contracts/

44. Scriptless scripts
◦ Smart contracts without use of a script
◦ No one can see the smart contract
◦ In this year maybe implemented in
bitcoin

45. Unlock song with signature
Schnorr 8000
Schnorr 7000
Initiate transaction
Schnorr 1000
Zero knowledge proof
Calculate Song Schnorr 7000
Broadcast Schnorr 8000
Finish transaction

46. Recommended
Reading
Dan Boney & Victor Shoup, A Graduate Course in Applied Cryptography
(September 2017, v0.4). https://crypto.stanford.edu/~dabo/cryptobook/
Applications of Modern Cryptography Technologies, applications and
choices (SURFNet, 2010)
https://www.surf.nl/binaries/content/assets/surf/en/knowledgebase/2010/rap
port_201009_SNcryptoWEB.pdf
Decrypted secrets. Methods & Maixms of Cryptology byF.L Bauer. (2007).
Bitcoin magazine (November 2017)
https://bitcoinmagazine.com/articles/scriptless-scripts-how-bitcoin-can-
support-smart-contracts-without-smart-contracts/
https://medium.com/beam-mw/mimblewimble-explained-like-youre-12-
d779a5bb483d
BIP Scnorr https://github.com/sipa/bips/blob/bip-schnorr/bip-
schnorr.mediawiki
@roywasse for slides