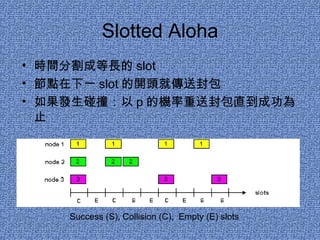
Pure (unslotted) ALOHA is simpler since packets are not required to transmit at the beginning of time slots, increasing the probability of collisions. The probability of successful transmission by a given node is equal to the probability the node transmits multiplied by the probability no other nodes transmit within the same time period. For slotted ALOHA, time is divided into equal length time slots and nodes transmit packets at the beginning of the next slot. If a collision occurs, packets will be retransmitted with probability p until successful. Slotted ALOHA can achieve higher efficiency, with the optimal transmission probability p approaching 1/e = 0.37 as the number of nodes increases, resulting in a maximum throughput of 37%

1. Pure (unslotted) ALOHA unslotted Aloha: 較簡單 , 非同步 封包不會等到在 slot 的開頭才傳送 會增加碰撞的機率

2. Pure Aloha P(success by given node) = P(node transmits) . P(no other node transmits in [p 0 -1,p 0 ] . P(no other node transmits in [p 0 -1,p 0 ] = p . (1-p) . (1-p) P(success by any of N nodes) = N p . (1-p) . (1-p) … choosing optimum p as n -> infty ... = 1/(2e) = .18 S = throughput = “goodput” (success rate) G = offered load = Np 0.5 1.0 1.5 2.0 0.1 0.2 0.3 0.4 Pure Aloha Slotted Aloha

3. Slotted Aloha 時間分割成等長的 slot 節點在下一 slot 的開頭就傳送封包 如果發生碰撞：以 p 的機率重送封包直到成功為止 Success (S), Collision (C), Empty (E) slots

4. Slotted Aloha 效率 假設有 N 個節點要傳送封包 每個 slot 以 p 的機率傳送封包 成功傳送的機率 S 為： 單一節點 : S= p (1-p) (N-1) 任意 N 節點 S = Prob ( 單一傳送 ) = N p (1-p) (N-1) … choosing optimum p as n -> infty ... = 1/e = .37 as N -> infty 最佳情況： 37% 頻道使用率