This document discusses formatting bits to better implement signal processing algorithms with integer arithmetic. It begins by introducing the context and objectives, which is to develop a methodology and tools to implement embedded filter algorithms using only integer arithmetic while controlling errors. It then discusses fixed-point arithmetic and how filters can be implemented using sum-of-products operations. The objective is given a bound on the final error, to find an implementation that reduces bit usage while controlling output error. The document proposes a two-step bit formatting method that first formats the most significant bits using Jackson's rule, then determines the minimum number of least significant bits that need to be kept to ensure faithful rounding of the final result.

1. Context and Objectives
Bits Formatting
Conclusion
Formatting bits to better implement signal
processing algorithms
e
Benoit Lopez - Thibault Hilaire - Laurent-St´phane Didier
PECCS 2014
January 9th 2014
1/20

2. Context and Objectives
Bits Formatting
Conclusion
Outline
1
Context and Objectives
2
Bits Formatting
3
Conclusion
2/20

3. Context and Objectives
Bits Formatting
Conclusion
In PECCS’14
Smartphone applications, measurement applications, embedded
devices, ...
3/20

4. Context and Objectives
Bits Formatting
Conclusion
In PECCS’14
Smartphone applications, measurement applications, embedded
devices, ...
Implementation problem
We need methodology and tools for the implementation of
embedded filter algorithms with only integer arithmetic.
3/20

5. Context and Objectives
Bits Formatting
Conclusion
On the first hand... A filter
x[n]
z
b0
+
+
z
+
+
h(z) =
1
z
Pn
1+
b1
i=0
Pn
bi z
1
y[n]
+
b1
a1
b2
z
a2
1
b3
x[n]
1
a1
1
b2
z
y[n]
+
z
b1
z
+
1
a2
z
1
z
1
z
1
i
i=1 ai z
i
z
1
b3
1
z
a3
1
a3
Signal Processing
LTI filters: FIR or IIR
Its transfer function
Algorithmic relationship used to compute output(s) from
input(s), for example:
n
y (k) =
i=0
n
bi u(k − i) −
i=1
ai y (k − i)
4/20

6. Context and Objectives
Bits Formatting
Conclusion
On the other hand... A target
...
↵
±2
s
2
...
2
0
2
↵
Hardware target (FPGA, ASIC) or software target (DSP,µC)
Due to resources constraints (cost, size, power consumption,
...) we have no FPU, so we can only use fixed-point arithmetic
5/20

7. Context and Objectives
Bits Formatting
Conclusion
Fixed-Point Arithmetic
Fixed-Point number
Fixed-point numbers are integers used to approximate real
numbers.
−2m 2m−1
Xm
20
2−1
2
X0
X−1
X
w
Representation : X .2 with X = Xm Xm−1 ...X0 ...X .
Format : determined by wordlength and fixed-point position,
and noted for example (m, ).
6/20

8. Context and Objectives
Bits Formatting
Conclusion
Fixed-Point Arithmetic
Fixed-Point number
Fixed-point numbers are integers used to approximate real
numbers.
−2m 2m−1
Xm
20
2−1
2
X0
X−1
X
w
Representation : X .2 with X = Xm Xm−1 ...X0 ...X .
Format : determined by wordlength and fixed-point position,
and noted for example (m, ).
Computation in finite precision and choice of formats imply errors.
Numerical degradations
quantization of the coefficients
round-off errors in computations
6/20

9. Context and Objectives
Bits Formatting
Conclusion
Filter
IIR Filter
Let H be the transfer function of a n − th order IIR filter :
H(z) =
b0 + b1 z −1 + · · · + bn z −n
,
1 + a1 z −1 + · · · + an z −n
∀z ∈ C.
(1)
7/20

10. Context and Objectives
Bits Formatting
Conclusion
Filter
IIR Filter
Let H be the transfer function of a n − th order IIR filter :
H(z) =
b0 + b1 z −1 + · · · + bn z −n
,
1 + a1 z −1 + · · · + an z −n
∀z ∈ C.
(1)
This filter is usually realized with the following algorithm
n
y (k) =
i=0
n
bi u(k − i) −
i=1
ai y (k − i)
(2)
where u(k) is the input at step k and y (k) the output at step k.
7/20

11. Context and Objectives
Bits Formatting
Conclusion
Filter
IIR Filter
Let H be the transfer function of a n − th order IIR filter :
H(z) =
b0 + b1 z −1 + · · · + bn z −n
,
1 + a1 z −1 + · · · + an z −n
∀z ∈ C.
(1)
This filter is usually realized with the following algorithm
n
y (k) =
i=0
n
bi u(k − i) −
i=1
ai y (k − i)
(2)
where u(k) is the input at step k and y (k) the output at step k.
We can see round-off errors as the add of an error e(k) on the
output and only y † (k) can be computed.
n
y † (k) =
i=0
n
bi u(k − i) −
i=1
ai y † (k − i) + e(k).
(3)
7/20

12. Context and Objectives
Bits Formatting
Conclusion
Filter
u(k)
e(k)
H
He
y(k)
∆y(k)
+
y † (k)
∆y (k) y † (k) − y (k) can be seen as the result of the error
through the filter He :
He (z) =
1
,
1 + a1 z −1 + · · · + an z −n
∀z ∈ C.
8/20

13. Context and Objectives
Bits Formatting
Conclusion
Filter
u(k)
e(k)
H
He
y(k)
∆y(k)
+
y † (k)
∆y (k) y † (k) − y (k) can be seen as the result of the error
through the filter He :
He (z) =
1
,
1 + a1 z −1 + · · · + an z −n
∀z ∈ C.
If the error e(k) is in [e; e], then we are able to compute ∆y and
∆y such that ∆y (k) is in [∆y ; ∆y ] :
∆y
=
∆y
=
e +e
e −e
|He |DC −
He
2
2
e +e
e −e
|He |DC +
He
2
2
∞
∞
8/20

14. Context and Objectives
Bits Formatting
Conclusion
Objective
Fixed-Point implementation and especially the choice of formats,
imply errors.
In the context of digital signal processing, we are able to control
these errors.
9/20

15. Context and Objectives
Bits Formatting
Conclusion
Objective
Fixed-Point implementation and especially the choice of formats,
imply errors.
In the context of digital signal processing, we are able to control
these errors.
Objective:
Given an algorithm and a bound on the final error, find an
implementation which reduces the number of bits of the
computation while controlling the error on the output result.
9/20

16. Context and Objectives
Bits Formatting
Conclusion
Outline
1
Context and Objectives
2
Bits Formatting
3
Conclusion
10/20

17. Context and Objectives
Bits Formatting
Conclusion
Sum-of-Products
The only operations needed in filter algorithm computation are
sum-of-products:
n
s=
i=1
n
ci · xi =
pi
i=1
where ci are known constants and xi variables (inputs, state or
intermediate variables).
In the context of filter design, we know the fixed-point format
of the final result.
11/20

18. Context and Objectives
Bits Formatting
Conclusion
Formatting
s
s
s
s
s
s
s
s
s
sf
Context
A sum of N terms (pi )1≤i≤N with different formats, and the known
FPF of final result (sf ), less than total wordlength (s).
12/20

19. Context and Objectives
Bits Formatting
Conclusion
Formatting
s
s
s
s
s
s
s
s
s
sf
Context
A sum of N terms (pi )1≤i≤N with different formats, and the known
FPF of final result (sf ), less than total wordlength (s).
Questions:
Can we remove bits that don’t impact the final result ? If we want
a faithful round-off of the final result, can we remove some bits ?
12/20

20. Context and Objectives
Bits Formatting
Conclusion
Formatting
s
s
s
s
s
s
s
s
s
sf
Two-step formatting
1
most significant bits
2
least significant bits
12/20

21. Context and Objectives
Bits Formatting
Conclusion
MSB formatting
Jacskon’s Rule (1979)
This Rule states that in consecutive additions and/or subtractions
in two’s complement arithmetic, some intermediate results and
operands may overflow. As long as the final result representation
can handle the final result without overflow, then the result is valid.
13/20

22. Context and Objectives
Bits Formatting
Conclusion
MSB formatting
Jacskon’s Rule (1979)
This Rule states that in consecutive additions and/or subtractions
in two’s complement arithmetic, some intermediate results and
operands may overflow. As long as the final result representation
can handle the final result without overflow, then the result is valid.
Example :
We want to compute 104 + 82 − 94 with 8 bits :
13/20

23. Context and Objectives
Bits Formatting
Conclusion
MSB formatting
Jacskon’s Rule (1979)
This Rule states that in consecutive additions and/or subtractions
in two’s complement arithmetic, some intermediate results and
operands may overflow. As long as the final result representation
can handle the final result without overflow, then the result is valid.
Example :
We want to compute 104 + 82 − 94 with 8 bits :
104 + 82 = −70 overflow !
13/20

24. Context and Objectives
Bits Formatting
Conclusion
MSB formatting
Jacskon’s Rule (1979)
This Rule states that in consecutive additions and/or subtractions
in two’s complement arithmetic, some intermediate results and
operands may overflow. As long as the final result representation
can handle the final result without overflow, then the result is valid.
Example :
We want to compute 104 + 82 − 94 with 8 bits :
104 + 82 = −70 overflow !
but −70 − 94 = 92 overflow !
This second overflow cancels the first one and we obtain the
expected result.
13/20

25. Context and Objectives
Bits Formatting
Conclusion
MSB formatting
Fixed-Point Jacskon’s Rule
Let s be a sum of n fixed-point number pi s, in format (M, L). If s
is known to have a final MSB equals to mf with mf < M, then:


mf +1
s=
1≤i≤n
mf

j=L
2j pi,j 
s
s
s
s
s
s
s
M
s
mf
L
s
sf
14/20

26. Context and Objectives
Bits Formatting
Conclusion
MSB formatting
Fixed-Point Jacskon’s Rule
Let s be a sum of n fixed-point number pi s, in format (M, L). If s
is known to have a final MSB equals to mf with mf < M, then:


mf +1
s=
1≤i≤n
mf

j=L
2j pi,j 
s
s
s
s
s
s
s s s
s
M
mf
L
s
sf
14/20

27. Context and Objectives
Bits Formatting
Conclusion
LSB formatting
LSB Formatting main idea
s
s
s
s
s
s
s
s
s
sf
15/20

28. Context and Objectives
Bits Formatting
Conclusion
LSB formatting
LSB Formatting main idea
s
s
s
s
s
s
s
s
s
sf
If we remove some bits, we will not compute sf anymore but a
faithful round-off of sf can be acceptable.
15/20

29. Context and Objectives
Bits Formatting
Conclusion
LSB formatting
LSB Formatting main idea
s
s
s
s
s
s
sδ
s
δ
s
sf
Can we determine a minimal δ such that sf is always a faithful
round-off of sf ?
15/20

30. Context and Objectives
Bits Formatting
Conclusion
LSB formatting
LSB Formatting main idea
s
s
s
s
s
s
sδ
s
δ
s
sf
δ evaluation
For both rounding mode (round-to-nearest or truncation), the
smallest integer δ that provides sf = lf (sf ) is given by:
δ = log2 (n)
15/20

31. Context and Objectives
Bits Formatting
Conclusion
Formatting
Formatting method
s
s
s
s
s
s
s
s
1
s
sf
we compute δ
16/20

32. Context and Objectives
Bits Formatting
Conclusion
Formatting
Formatting method
s
s
s
s
s
s
sδ
s
δ
s
1
2
sf
we compute δ
we format all pi s into FPF (mf , lf − δ)
16/20

33. Context and Objectives
Bits Formatting
Conclusion
Formatting
Formatting method
s
s
s
s
sδ
s
δ
s
1
2
3
sf
we compute δ
we format all pi s into FPF (mf , lf − δ)
we compute sδ
16/20

34. Context and Objectives
Bits Formatting
Conclusion
Formatting
Formatting method
s
s
s
s
sδ
s
δ
s
1
2
3
4
we
we
we
we
sf
compute δ
format all pi s into FPF (mf , lf − δ)
compute sδ
obtain sf from sδ
16/20

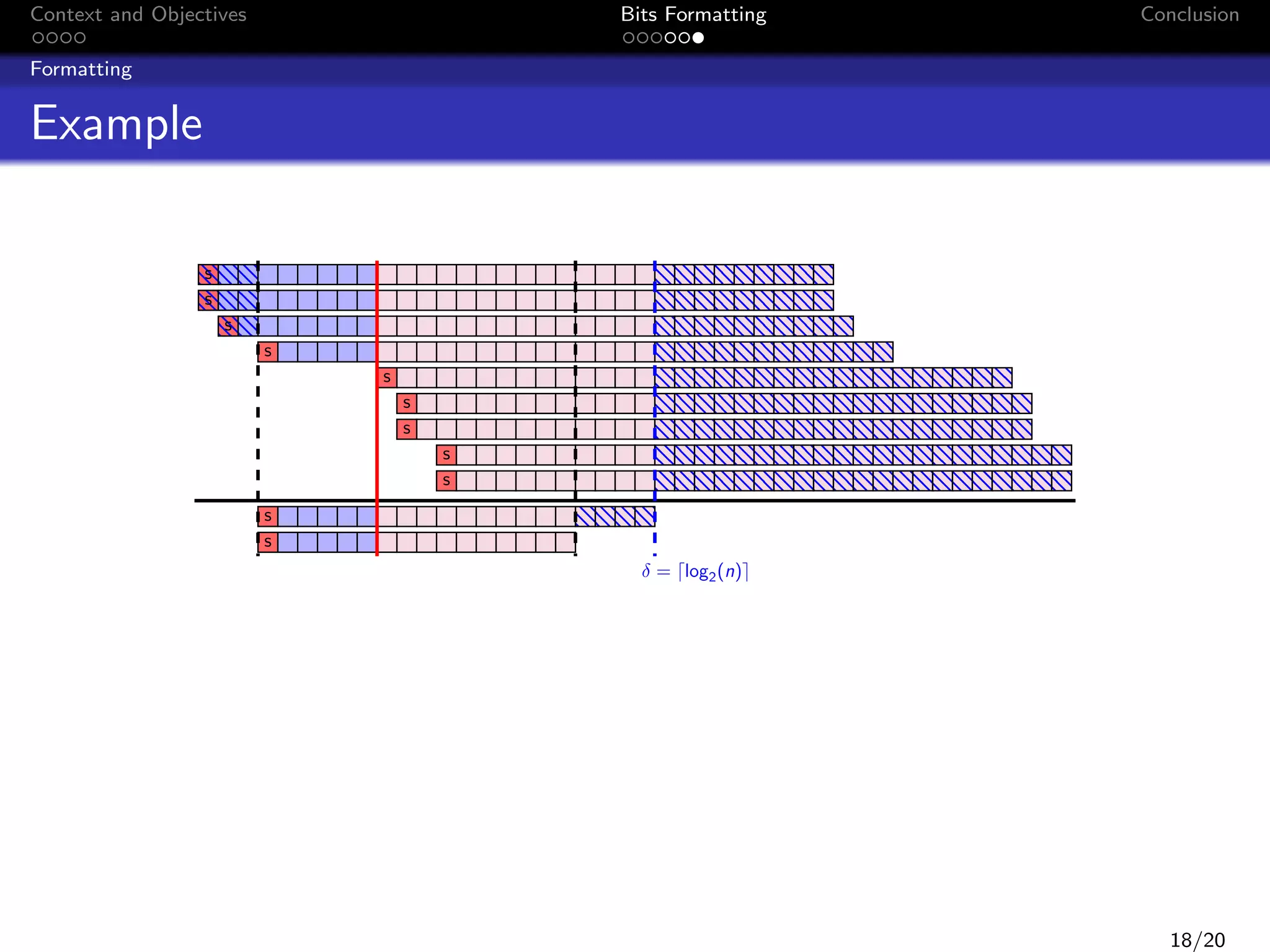
35. Context and Objectives
Bits Formatting
Conclusion
Formatting
Example
The following algorithm is the fixed-point algorithm of a 4th −order
butterworth filter:
y (k) = 0.0013279914856 u(k) + 0.00531196594238 u(k − 1)
+0.00796794891357 u(k − 2) + 0.00531196594238 u(k − 3)
+0.0013279914856 u(k − 4) + 2.87109375 y (k − 1)
−3.20825195312 y (k − 2) + 1.63458251953 y (k − 3)
−0.318710327148 y (k − 4)
Inputs datas :
wordlength of constants, u(k) and y (k) : 16 bits
u(k) ∈ [−13, 13]
17/20

36. Context and Objectives
Bits Formatting
Conclusion
Formatting
Example
The following algorithm is the fixed-point algorithm of a 4th −order
butterworth filter:
y (k) = 0.0013279914856 u(k) + 0.00531196594238 u(k − 1)
+0.00796794891357 u(k − 2) + 0.00531196594238 u(k − 3)
+0.0013279914856 u(k − 4) + 2.87109375 y (k − 1)
−3.20825195312 y (k − 2) + 1.63458251953 y (k − 3)
−0.318710327148 y (k − 4)
Inputs datas :
wordlength of constants, u(k) and y (k) : 16 bits
u(k) ∈ [−13, 13] and y (k) ∈ [−17.123541; 17.123541]
17/20

37. Context and Objectives
Bits Formatting
Conclusion
Formatting
Example
s
s
s
s
s
s
s
s
s
s
s
18/20

38. Context and Objectives
Bits Formatting
Conclusion
Formatting
Example
s
s
s
s
s
s
s
s
s
s
s
δ = log2 (n)
18/20

39. Context and Objectives
Bits Formatting
Conclusion
Conclusion
We try to answer the following question :
For a given sum-of-products, how to reduce the number of bits of
the operands while controlling the error ?
For this, some works have been realized:
FiPoGen : a tool generating fixed-point code for a given
sum-of-products
Bits formatting : a first step towards word-length optimization
19/20

40. Context and Objectives
Bits Formatting
Conclusion
THANK YOU
Any questions?
20/20