sheet6.pdf

January 24, 2012 1
Cryptography and Network Security
Lecture 5: Basic notions of finite fields
Ion Petre
Department of IT, Åbo Akademi University
Spring 2012
http://users.abo.fi/ipetre/crypto/

Content of this lecture
January 24, 2012 http://users.abo.fi/ipetre/crypto/ 2
Z Zp
Zp[X] GF(pn)
Modular
arithmetics
Modular
arithmetics
Polynomials
Every finite field
has this structure
Domain of
operation
of AES

January 24, 2012 3
Why finite fields?
 Increasingly important in cryptography
 Several modern cryptographic algorithms rely on computations in various finite fields, among them
AES and elliptic curve cryptography
 AES uses arithmetic in the finite field GF(28)
 Virtually all modern encryption algorithms (both symmetric and public-key) involve
arithmetic operations on integers
 If we decide to work on n-bit integers, for efficiency of storage we would like to be able to use all
integers on n-bits
 This means we have to do operations on integers from 0 to 2n-1
 We could decide to use operations in Zm, where m=2n
 Difficulty 1: we may need to do divisions and Zm is not a field
 Difficulty 2: arithmetic modulo 2n may give rise to weak cryptographic algorithms
 Example: suppose we work with 3-bit blocks and decide to do arithmetic modulo 8
 In the multiplication table of Z8, 1,2,…,7 appear with different frequency: 1 occurs 4 times, 2 occurs
8 times, 3 occurs 4 times, 4 occurs 12 times, 5 occurs 4 times, 6 occurs 8 times, 7 occurs 4 times
 Solution: use a finite field GF(23) with 8 elements – division is always possible and in the
multiplication table each integer 1,…,7 occurs exactly 7 times

January 24, 2012 4
Why finite fields?
 We need fields: y=ax+b  x=a-1(y-b)
 We need finite fields
 They all have pn elements, with p a prime number
 What is their structure (addition, multiplication table)
 Are there many different fields with pn elements?
 Example: a field with 8 elements

January 24, 2012 5
Modulo 8 example
This is not a field!

January 24, 2012 6
A field with 8 elements!
+ 0 1 2 3 4 5 6 7
0 0 1 2 3 4 5 6 7
1 1 0 3 2 5 4 7 6
2 2 3 0 1 6 7 4 5
3 3 2 1 0 7 6 5 4
4 4 5 6 7 0 1 2 3
5 5 4 7 6 1 0 3 2
6 6 7 4 5 2 3 0 1
7 7 6 5 4 3 2 1 0
X 0 1 2 3 4 5 6 7
0 0 0 0 0 0 0 0 0
1 0 1 2 3 4 5 6 7
2 0 2 4 5 3 1 7 5
3 0 3 6 5 7 4 1 2
4 0 4 3 7 6 2 5 1
5 0 5 1 4 2 7 3 6
6 0 6 7 1 5 3 2 4
7 0 7 5 2 1 6 4 3

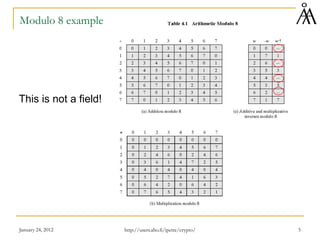
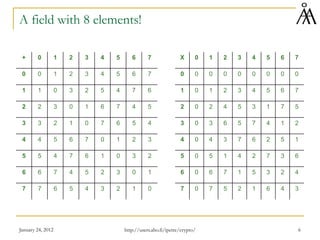
January 24, 2012 7
Summary of the constructions in this lecture
 Consider the integers Z
 Take a prime number p and do operations modulo p: Zp is a field with
p elements (order p)
 Consider polynomials with coefficients in Zp: Zp[X]
 Take an irreducible polynomial m(x) of degree n and do operations
modulo m(x): GF(pn) is a field with pn elements (order pn)
 AES uses GF(28) with arithmetic modulo x8+x4+x3+x+1

January 24, 2012 8
Plan of the lecture
 Introduce here (minimal) notions needed for the understanding of AES
 Groups, rings, fields
 Divisors, modular arithmetic
 Euclid’s algorithm
 Polynomial arithmetic

January 24, 2012 9
Basic notions of abstract algebra:
groups, rings, fields
 Group (G,¤,e): a set G with a binary operation ¤ and an element e∈G
satisfying the following laws:
 Associativity: a ¤ (b ¤ c)=(a ¤ b) ¤ c for any a,b,c∈G
 Identity element: a ¤ e=e ¤ a=a, for any a∈G
 Inverse element: for each a∈G, there exists an element a’∈G such that a ¤ a’=
a’ ¤ a=e.
 a’ is usually denoted as -a and is called the inverse of a
 Example of a group: the set of integers with the addition (Z,+,0)
 Note that the set of integers with the multiplication (Z,x,1) is not a group: the
inverse element does not exist for all integers (it exists only for 1 and –1)

January 24, 2012 10
Groups
 A group (G, ¤,e) is called:
 Commutative (or abelian) if a ¤ b=b ¤ a for all a,b in G
 Finite if set G is finite
 Infinite if set G is infinite
 Example:
 (Z,+,0) is a commutative group
 The set of nxn matrices over integers, with the addition, is a commutative
group
 The set of permutations of the set {1,2,…,n} with the composition, is a finite
non-commutative group

January 24, 2012 11
Rings
 Ring (R,+,•,0,1): a set R with two binary operations + and • satisfying the following laws:
 Associative addition: (a+b)+c=a+(b+c)
 Existence of 0: a+0=0+a=a
 Existence of the inverse: for all a, there is –a such that a+(-a)=(-a)+a=0
 Commutativity of addition: a+b=b+a
 Associative multiplication: a•(b•c)=(a•b)•c for any a,b,c∈R
 Existence of 1: a•1=1•a=a
 Distributivity of • over +: a•(b+c)=a•b + a•c; (a+b)•c=a•c + b•c
 A ring (R,+,•,0) is called commutative if the multiplication • is commutative
 Example:
 (Z,+,•,0,1) is an integral domain
 (Z26, +,•,0,1) is a commutative unitary ring, but not an integral domain: 2•13=0 (mod 26)
 The set of nxn matrices over integers with addition and multiplication is a commutative unitary
ring, but not an integral domain

January 24, 2012 12
Fields
 Field (F,+,•,0,1):
 (F,+, •,0,1) is a ring
 Commutativity of the multiplication
 Multiplicative inverse: for any nonzero element a in F there exists an
element a’ in F such that a•a’=a’•a=1
 a’ is usually denoted as a-1 and it is called the multiplicative inverse of a
 Example:
 The set of rational numbers (Q,+,•,0,1), the set of real numbers (R,+,•,0,1)
are fields
 The set of integers (Z,+, •,0,1) is not a field: only 1 and –1 have
multiplicative inverses
 (Z26, +, •,0,1) is not field
 (Z3,+, •,0,1) is a finite field: the inverse of 1 is 1 and the inverse of 2 is 2
 (Z5,+, •,0,1) is a finite field: 1•1=1 mod 5, 2•3=1 mod 5, 4•4=1 mod 5
 Inverse of 1 is 1, inverse of 2 is 3, inverse of 3 is 2, inverse of 4 is 4

January 24, 2012 13
Modular arithmetic
 Consider now the set of integers: fix a positive integer n
 For any integer a, there exists integers q and r such that a=qn+r and
r is from 0 to n-1
 q is the largest integers less than or equal to a/n
 r is called the residue of a modulo n
 Define the operator mod: a mod n=r
 Define the operator div: a div n=q
 Example:
 7 mod 5 = 2, 11 mod 7 =4,
 -11 mod 7 =3: -11=(-2).7+3
 Congruence modulo n: a≡b mod n if a mod n = b mod n
 Example: 73 ≡ 4 mod 23, 21 ≡ -9 ≡ 1mod 10

January 24, 2012 14
Modulo 7 Example
 The elements in each column are congruent to each other modulo 7
...
-21 -20 -19 -18 -17 -16 -15
-14 -13 -12 -11 -10 -9 -8
-7 -6 -5 -4 -3 -2 -1
0 1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31 32 33 34
...

January 24, 2012 15
Arithmetic modulo n
 We can perform ordinary arithmetic (addition, subtraction,
multiplication) modulo n (as we have done in Caesar)
 Useful properties (reduce the computation mod n at any step)
 (a+b) mod n = ( (a mod n) + (b mod n) ) mod n
 (a-b) mod n = ( (a mod n) - (b mod n) ) mod n
 (a•b) mod n = ( (a mod n) • (b mod n) ) mod n
 Example: to compute 117 mod 13 we do:
 112=121=4 mod 13
 114=42=3 mod 13
 117= 4•3•11 mod 13 =2 mod 13
 (Zn,+,•,0,1) is a commutative ring, where Zn= {0,1,2,…,n-1} and the
operations are performed modulo n

January 24, 2012 16
Arithmetic modulo n: divisions
 Careful when performing operations modulo n
 If (a+b) ≡ (a+c) mod n, then b ≡ c mod n
 Not true that if (a•b) ≡ (a•c) mod n, then b ≡ c mod n
 Example: (2•1) ≡ (2•5) mod 8 but 1 and 5 are not congruent modulo 8
 The implication is true if and only if a is relatively prime to n, i.e.,
gcd(a,n)=1
 Any such a has a multiplicative inverse a-1 modulo n

January 24, 2012 17
Modulo 8 example

January 24, 2012 18
Divisors
 A nonzero integer b divides a if a=mb, for some integer m. We
denote it as b | a and we say that b is a divisor of a
 Example: Positive divisors of 24 are 1,2,3,4,6,8,12,24
 Facts:
 If a | 1, then a=1 or a=-1
 If a | b and b | a, then a=b or a=-b
 If d | g and d | h, then d | (mg+nh), for any integers m and n
 If a ≡ b (mod n), then n | (a-b)
 If a ≡ b (mod n), then b ≡ a (mod n)
 If a ≡ b (mod n) and b ≡ c (mod n), then a ≡ c (mod n)

January 24, 2012 19
Greatest common divisor
 The positive integer d is the greatest common divisor of integers a and b,
denoted d=gcd(a,b) if
 It is a divisor of both a and b
 Any other divisor of a and b is a divisor of d
 Example: gcd(8,12)=4, gcd(24,60)=12
 Integers a and b are called relatively prime if gcd(a,b)=1
 Computing gcd(a,b): Euclid’s algorithm
 Based on the following fact: gcd(a,b)=gcd(b,a mod b)
 Euclid's Algorithm to compute gcd(a,b): Euclid(a,b)
 If b=0 then return a
 Else return Euclid(b,a mod b)
 Note: the algorithm always terminates

January 24, 2012 20
Example: d=gcd(1970,1066)
1970 = 1 x 1066 + 904 d= gcd(1066, 904)
1066 = 1 x 904 + 162 d= gcd(904, 162)
904 = 5 x 162 + 94 d= gcd(162, 94)
162 = 1 x 94 + 68 d= gcd(94, 68)
94 = 1 x 68 + 26 d= gcd(68, 26)
68 = 2 x 26 + 16 d= gcd(26, 16)
26 = 1 x 16 + 10 d= gcd(16, 10)
16 = 1 x 10 + 6 d= gcd(10, 6)
10 = 1 x 6 + 4 d= gcd(6, 4)
6 = 1 x 4 + 2 d= gcd(4, 2)
4 = 2 x 2 + 0 d= 2
Result: gcd(1970,1066)=2, i.e., the last nonzero residue in the above
computation

January 24, 2012 21
Finite fields
 Fields with a finite number of elements: what is their structure?
 It can be proved that if a field is finite then it has pn elements, for
some prime number p
 We also say that it has order pn
 We denote GF(pn) – GF stands for Galois field
 For n=1 we have GF(p) which is Zp
 If p is prime, then any element in Zp has a multiplicative inverse
 For n>1 the field has a different structure
 Start from Zp and build a field with pn elements

January 24, 2012 22
Example:
GF(7)=Z7

January 24, 2012 23
Finding the multiplicative inverse in Zp
 Given an element p, how do we calculate p-1?
 Euclid's Algorithm to compute gcd(a,b): Euclid(a,b)
 Result: if d=gcd(a,b), then there are integers x,y such that d=ax+by
 Consequence: if gcd(a,b)=1, then there are intergers x,y such that
ax+by=1
 so, ax=1 mod b, i.e., x=a-1 mod b
 Question: how do we calculate x for given a,b?
 Idea: run Euclid’s algorithm in such a way as to compute not only d, but also
x and y

Finding the multiplicative inverse in Zp
 Extended Euclid’s algorithm: ExtEuclid(a,b)
 Output: (d,x,y), where d=gcd(a,b) and d=ax+by
 If d=1, then x = a-1 (mod b)
 if b = 0 then return (a,1,0)
 else (t1,t2,t3)=ExtEuclid(b, a mod b)
 return (t1, t3, t2 – (a div b) * t3 )
 Proof of correctness
 Clearly, gcd is returned on the first component (runs like Euclid’s algorithm)
 Denote a mod b=r, a div b=z: a=bz+r
 The proof goes by induction
 The base case for b=0: trivial
 Induction step: if t1=gcd(b, r) and t1=t2*b+t3*r, then t1=t2*b+t3*(a-bz) and so,
t1=t3*a+(t2-t3*z)*b
January 24, 2012 http://users.abo.fi/ipetre/crypto/ 24

January 24, 2012 25
Example: the inverse of 550 in GF(1759)
 Extended Euclid’s algorithm: ExtEuclid(a,b)
 Output: (d,x,y), where d=gcd(a,b) and d=ax+by
 if b = 0 then return (a,1,0)
 else (t1,t2,t3)=ExtEuclid(b, a mod b)
 return (t1, t3, t2 - (a div b) * t3 )
 Z=ExtEuclid(550,1759): 550 =0•1759 + 550
 compute Z1=ExtEuclid(1759,550): 1759=3•550 + 109
 compute Z2=ExtEuclid(550,109): 550=5 •109 + 5
 compute Z3=ExtEuclid(109,5): 109=21•5+4
 compute Z6=ExtEuclid(1,0)=(1,1,0)
 Z5=(1,0,1), Z4=(1,1,-1), Z3=(1,-1,22), Z2=(1,22,-111), Z1=(1,-111,355)
 Z=(1,355,-111)
 Final answer: the inverse of 550 mod 1759 is 355

January 24, 2012 26
Polynomial Arithmetic
 To define GF(pn) we need to discuss about operations with
polynomials with coefficients in Zp: polynomial arithmetic
 Consider only polynomials in one indeterminate

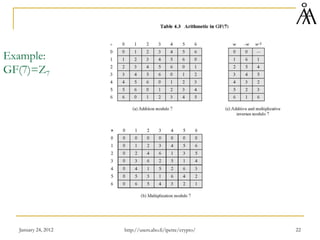
January 24, 2012 27
Ordinary Polynomial Arithmetic
 Consider polynomials with coefficients in a ring or a field – e.g, Z
 Adding/subtracting two polynomials is done by adding/subtracting the
corresponding coefficients
 Multiplying two polynomials is done in the usual way, by multiplying all terms
with each other
 Division (not necessarily exact) of two polynomials can also be defined if the
coefficients are in a field
 Example: f(x) = x3 + x2 + 2, g(x) = x2 – x + 1 with coefficients in Z
 f(x) + g(x) = x3 + 2x2 – x + 3
 f(x) – g(x) = x3 + x + 1
 f(x) x g(x) = x5 + 3x2 – 2x + 2
 For a ring or a field R, (R[X],+,•,0,1) is a ring – the ring of polynomials over R

January 24, 2012 28
Polynomial Arithmetic with Modulo Coefficients
 Consider polynomials with coefficients in Zp, for some prime p
 We are mostly interested in computations mod 2: all coefficients are
0 or 1
 Example: f(x) = x3 + x2 and g(x) = x2 + x + 1
f(x) + g(x) = x3 + x + 1
f(x) x g(x) = x5 + x2
 Division (not necessarily exact) of two polynomials can also be
defined if the coefficients are in a field
 The computations are done similarly as for integers: e.g., Euclid’s
algorithm holds also for polynomials

January 24, 2012 29
Division of polynomials with coefficients in Zp
 For any polynomials f(x), g(x), there exist two polynomials q(x), r(x) such that:
 f(x) = q(x) g(x) + r(x)
 deg(r) < deg(g)
 Thus, division (not necessarily exact) is possible:
 q(x)=f(x) div g(x)
 r(x)=f(x) mod g(x)
 If r(x)=0, then we say that g(x) divides f(x): g(x) | f(x)
 If f(x) has no divisors other than itself and constant polynomials, we say it is
irreducible (or prime) polynomial
 Equivalently, f(x) cannot be written as g(x)h(x) with deg(g) < deg(f), deg(h) < deg(f)
 Greatest common divisor gcd(f,g) is defined similarly as for integers:
 It is a divisor of both f and g
 Any other divisor of f and g is a divisor of gcd(f,g)
 Gcd(f,g) can be computed using Euclid’s algorithm

January 24, 2012 30
Computing the GCD of two polynomials over Zp
 Euclid(a,b)
 EUCLID[a(x), b(x)]: computes gcd(a(x), b(x))
 If b(x)=0 then return a(x)
 Else return EUCLID(b(x), a(x) mod b(x))

January 24, 2012 31
Modular Polynomial Arithmetic
(arithmetic modulo a polynomial)
 Consider an irreducible polynomial f(x) with degree n and coefficients in Zp
 Example: x8+x4+x3+x+1 is irreducible in Z2[x] (the polynomial used in AES)
 Polynomial arithmetic modulo f(x) can be done similarly as integer arithmetic
modulo a prime number p
 Take any two polynomials modulo f(x)
 Do addition/subtraction/multiplication modulo f(x)
 If f(x) is irreducible, then the set of all polynomials modulo f(x) forms a field
denoted GF(pn)
 We are mostly interested in GF(2n) : all polynomials with binary coefficients
and degree less than n
 Addition is the normal addition of two polynomials
 Multiplication is done modulo f(x)
 GF(2n) is indeed a field: any nonzero element has an inverse
 The extended Euclid algorithm can be used here just like for integers

January 24, 2012 32
Computing the inverse in GF(pn)
 Extended Euclid’s algorithm: ExtEuclid(a(x),b(x))
 Output: (d(x),e(x),f(x)), where d(x)=gcd(a(x),b(x)) and d=a(x)e(x)+b(x)f(x)
 if b(x) = 0 then return (a(x),1,0)
 else (t1(x),t2(x),t3(x))=ExtEuclid(b(x), a(x) mod b(x))
 return (t1(x), t3(x), t2(x) - (a(x) div b(x)) * t3(x) )
 If F(x) is an irreducible polynomial and (d(x),t(x),u(x))=ExtEuclid(a(x),F(x)), then
 d(x)=1
 t(x)=a-1(x) mod F(x)

January 24, 2012 33
Example: GF(23)

January 24, 2012 34
Computational considerations
 A polynomial in GF(2n)
can be represented by its n binary coefficients (an-1,an-2,…,a0), i.e., by a number on n
bits
 Addition of polynomials becomes bitwise XOR of their n-bit representations
 Multiplication is shift & XOR: example for GF(28) with m(x)=x8+x4+x3+x+1 (AES)
 x8 mod m(x) = (x8 - m(x)) = x4+x3+x+1
 Consider a polynomial in GF(28) f(x)=b7x7+b6x6+b5x5+b4x4+b3x3+b2x2+b1x+b0
 Multiplying by x we have xf(x)=b7x8+b6x7+b5x6+b4x5+b3x4+b2x3+b1x2+b0x
 If b7=0, then the result is in GF(28). If b7=1, then we need to reduce x8 mod m(x):
xf(x) = (b6x7+b5x6+b4x5+b3x4+b2x3+b1x2+b0x) + (x4+x3+x+1)
 Thus, multiplication by x is in fact a 1-bit left shift followed by a conditional XOR with
(00011011)
 Multiplication by higher powers of x implies an iteration of the above procedure

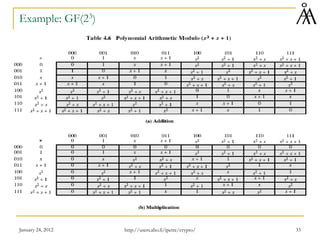
January 24, 2012 35
Summary
 Consider the integers Z
 Take a prime number and do operations modulo p: Zp is a field with p
elements (order p)
 Consider polynomials with coefficients in Zp: Zp[X]
 Take an irreducible polynomial m(x) of degree n and do operations
modulo m(x): GF(pn) is a field with pn elements (order pn)
 Any finite field has order pn, for some prime p and a positive integer n
 AES uses GF(28) with arithmetic modulo x8+x4+x3+x+1

sheet6.pdf

More Related Content

Similar to sheet6.pdf

More from aminasouyah

Recently uploaded

sheet6.pdf