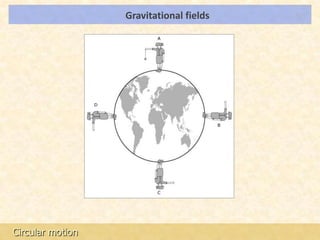
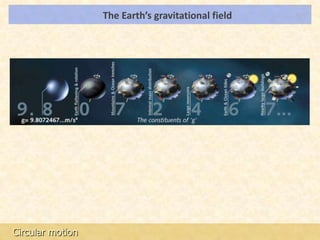
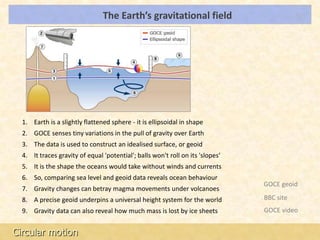
This document provides an introduction to gravitation and gravitational fields. It discusses how masses create gravitational fields, how field lines are used to represent these fields, and how gravitational field strength is measured as force per unit mass. It also addresses the gravitational field of the Earth specifically, how it varies slightly due to the Earth's shape, and how precise models of the geoid are constructed from gravitational data.

1. A-level Physics
A-level Physics
Unit G484:
The Newtonian
World
Gravitation -- introduction
Gravitation introduction
Circular motion

2. Gravitation LOs
Write down anything and everything you know
about ‘gravity’.
Circular motion

3. Lesson focus
• Gravitation - introduction
Learning objectives
At the end of the lesson you will be able to:
• describe how a mass creates a gravitational field in the
space around it;
• describe gravitational field strength as force per unit mass.
Circular motion

4. Learning outcomes
All of you should be able to
• explain the meaning of gravitational field;
• use field lines to show the gravitational field in a small region of the
Earth’s surface, and around the whole Earth;
• explain the meaning of gravitational field strength.
Most of you will be able to
• solve problems involving the shape and strength of a gravitational
field.
Circular motion

5. Fields of force LOs
Draw a diagram to show the magnetic field around a bar magnet.
Questions
1. Where is the field strongest?
3. How does your diagram show this?
4. How could you show that there is a ‘field’ around the magnet?
Circular motion

6. Fields of force LOs
Circular motion

7. Fields of force LOs
1/4 A field is a region where a specific test object experiences a force. A test
object interacts with the field but is small enough not to change the field.
Fields are represented with field lines. These show the direction of the
force on the object. The strength of the field is shown by the spacing of
the field lines (closer = stronger).
Circular motion

8. Gravitational fields LOs
1. What is the gravitational field like in this lab?
2. How can we test the field?
Circular motion

9. Gravitational fields LOs
2/4 A gravitational field is a region in which a mass experiences a force
of gravity. Gravitational field lines show the direction of force on a
test mass. Over small regions of the Earth’s surface they are
vertical, parallel and evenly spaced.
Circular motion

10. Gravitational fields LOs
Circular motion

11. Gravitational fields LOs
3/4 The gravitational field of the Earth as a whole is (broadly*) radial – field lines
come from infinity and converge at the centre of the Earth.
* Density variations within the Earth mean that it is not perfectly radial.
Circular motion

12. The Earth’s gravitational field LOs
Circular motion

13. The Earth’s gravitational field LOs
1. Earth is a slightly flattened sphere - it is ellipsoidal in shape
2. GOCE senses tiny variations in the pull of gravity over Earth
3. The data is used to construct an idealised surface, or geoid
4. It traces gravity of equal 'potential'; balls won't roll on its 'slopes‘
5. It is the shape the oceans would take without winds and currents
6. So, comparing sea level and geoid data reveals ocean behaviour
GOCE geoid
7. Gravity changes can betray magma movements under volcanoes
8. A precise geoid underpins a universal height system for the world BBC site
9. Gravity data can also reveal how much mass is lost by ice sheets GOCE video
Circular motion

14. Gravitational fields LOs
From this it can be seen that the force of gravity follows an
inverse-square law.
How do we write this? F  1/d2
Circular motion

15. What is the force of gravity? LOs
4/4 • The force of gravity is an attractive force between masses.
• It is the weakest of the four fundamental forces.
Gravitational field strength
The strength of a gravitational field is found by placing a test mass in the
field and is expressed as the force per unit mass, ‘g’
F units: N
g =
m kg
The Earth has a gravitational field strength of approximately 9.81 N kg-1 .
Circular motion

16. Introductory Qs LOs
1. In a solar eclipse the Sun, Moon and Earth lie in a
straight line. Show on a diagram the gravitation
forces which are exerted on the Moon at this point
and the direction in which they act. A scale diagram
is not required.
2. In travelling from the Earth to the Moon, American
astronauts experienced gravitation forces. On a
suitable graph, sketch the variation in gravitational
field strength that they experienced during the trip.
Circular motion

17. Introductory Qs LOs
Circular motion

18. Introductory Qs LOs
3. If it were possible to position a huge mass of small size (e.g. a
neutron ball) just above the Earth’s surface, what would be the
shape of the gravitational field around the mass?
4. A mass of 7 kg is placed on a spring balance 1 m above the
surface of the Earth and experiences a force of 68.67 N.
Calculate the gravitation field strength at that point.
5. The gravitational force on a mass m on the Moon is 1.7m. Use
this information to calculate the ratio of g on the Earth to that on
the Moon.
Circular motion