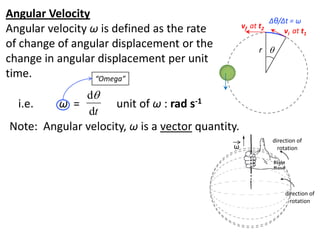
Angular displacement (θ) is defined as the arc length (s) divided by the radius (r) of the arc. One radian is equal to an arc length that is equal to the radius. Angular velocity (ω) is the rate of change of angular displacement with respect to time. It describes the change in angular displacement per unit time and has units of radians per second. For uniform circular motion, the angular velocity is constant. Centripetal acceleration is the acceleration experienced by an object moving in a circular path, directed toward the center. The centripetal force causing this acceleration is given by mv^2/r.

1. flipperworks.com

2. flipperworks.com
Angular Displacement
Angular displacement  is defined:
arc length s
θ= radius of arc
= and θ = 1 radian (rad) when s = r
r
For one complete revolution, s
cir. of circle θ
θ =
radius of arc
r
= 2 = 2π rad
r
r
o
To convert  in degrees to radians:  (rad) = o
 2
360
Note: rad is physically dimensionless as it is the ratio of
two lengths.

3. flipperworks.com
Angular Velocity Δθ/Δt = ω
Angular velocity ω is defined as the rate vf at t2
vi at t1
of change of angular displacement or the r 
change in angular displacement per unit
time. “Omega”
d
i.e. ω = unit of ω : rad s-1
dt
Note: Angular velocity, ω is a vector quantity.
direction of
ω rotation
direction of
rotation

4. flipperworks.com
Angular Velocity Δθ/Δt = ω
Angular velocity ω is defined as the rate vf at t2
vi at t1
of change of angular displacement or the r 
change in angular displacement per unit
time. “Omega”
d
i.e. ω = unit of ω : rad s-1
dt
Note: Angular velocity, ω is a vector quantity.
Consider an object moving with speed v in a circular path
of radius r:
d d  s  1 ds v
ω = =    v = rω
dt dt  r  r dt r

5. flipperworks.com
For uniform circular motion, since v has the same
magnitude throughout the motion, angular velocity is
a constant.
If T is the time taken to complete one revolution then
2
ω 
T
T is known as the period. Do you know how T and f is
related?
1
f  unit of f : Hertz (Hz)
T

6. flipperworks.com
Centripetal Acceleration
In a uniform circular motion, the velocity is always
changing, the motion is accelerated and by Newton’s
second law, a resultant force must be acting on it.
vi vf
A B
vf Δv
- vi
Δv = vf – vi
C = vf + (- vi)
where a is the
centripetal acceleration

7. flipperworks.com
The force causing the circular motion is known as the
centripetal force and is given by
mv 2
F = = mrω2
r
Points to note:
• centripetal force should not be drawn as an additional
force in force diagrams
• if there is no centripetal force an object in circular
motion would fly off in a direction tangent to the circular
path
• since the centripetal force acts at right angles to the
motion, the centripetal force does no work (centripetal
force does not change the speed of the object)

8. flipperworks.com

9. flipperworks.com