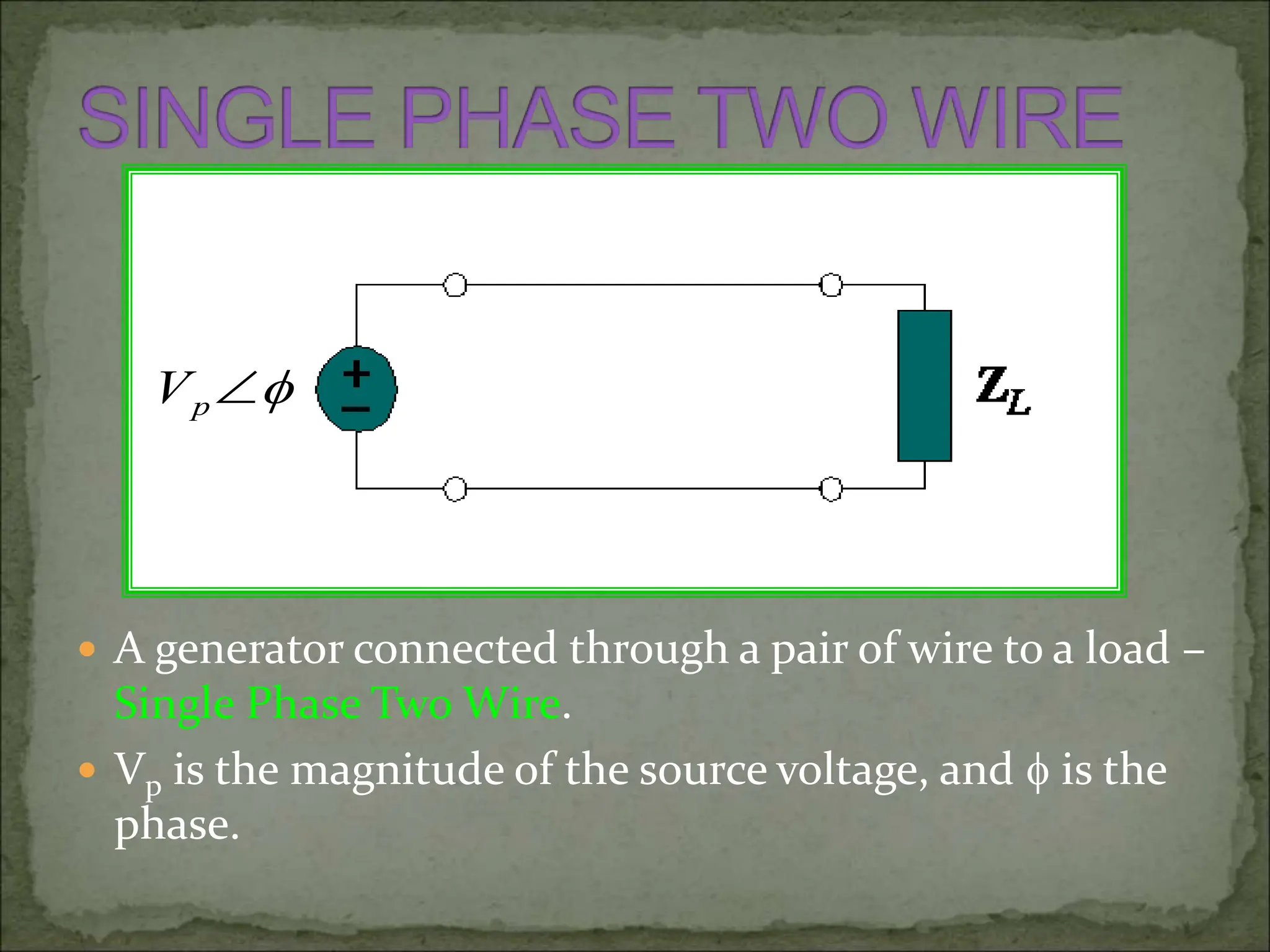
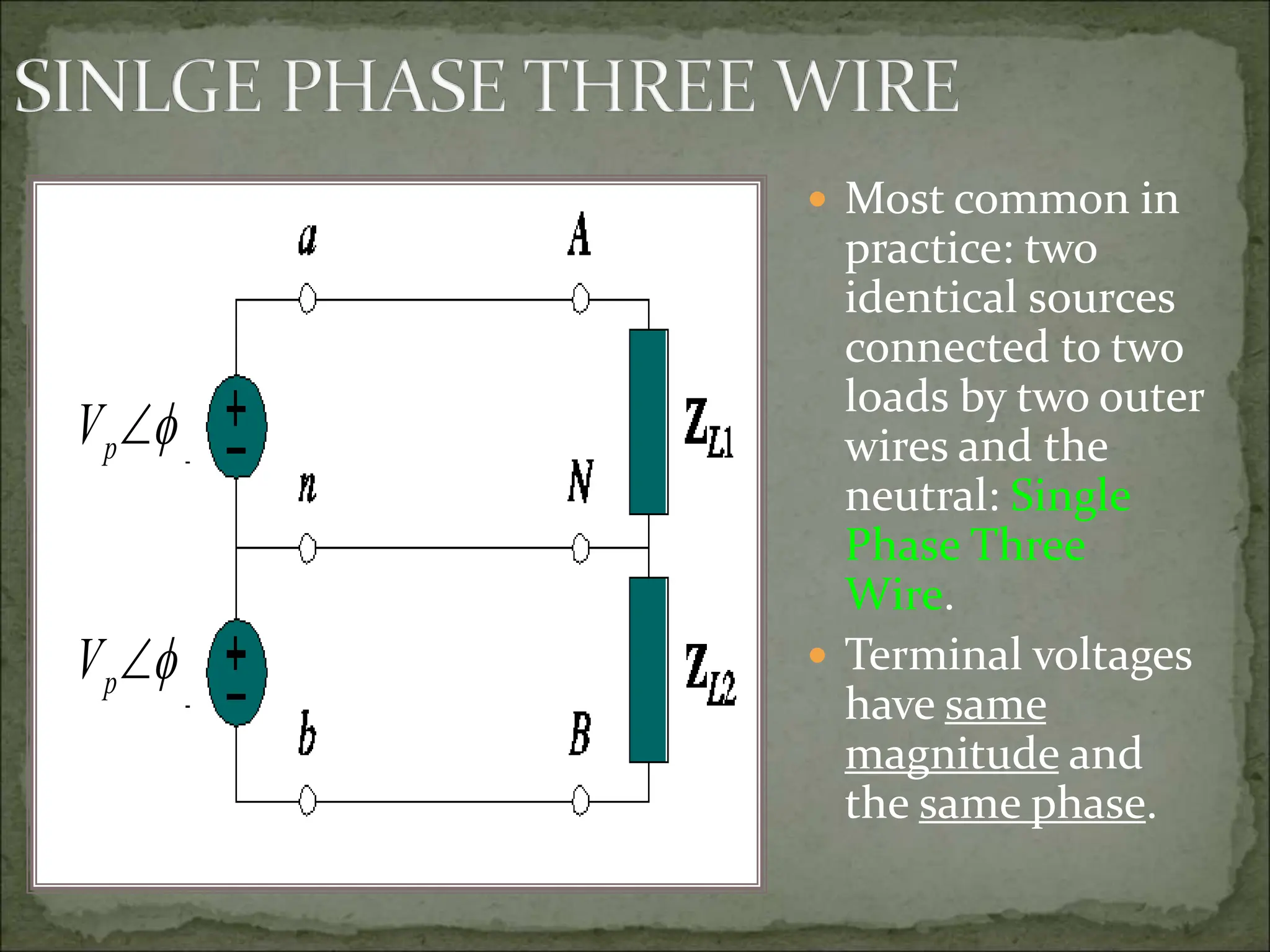
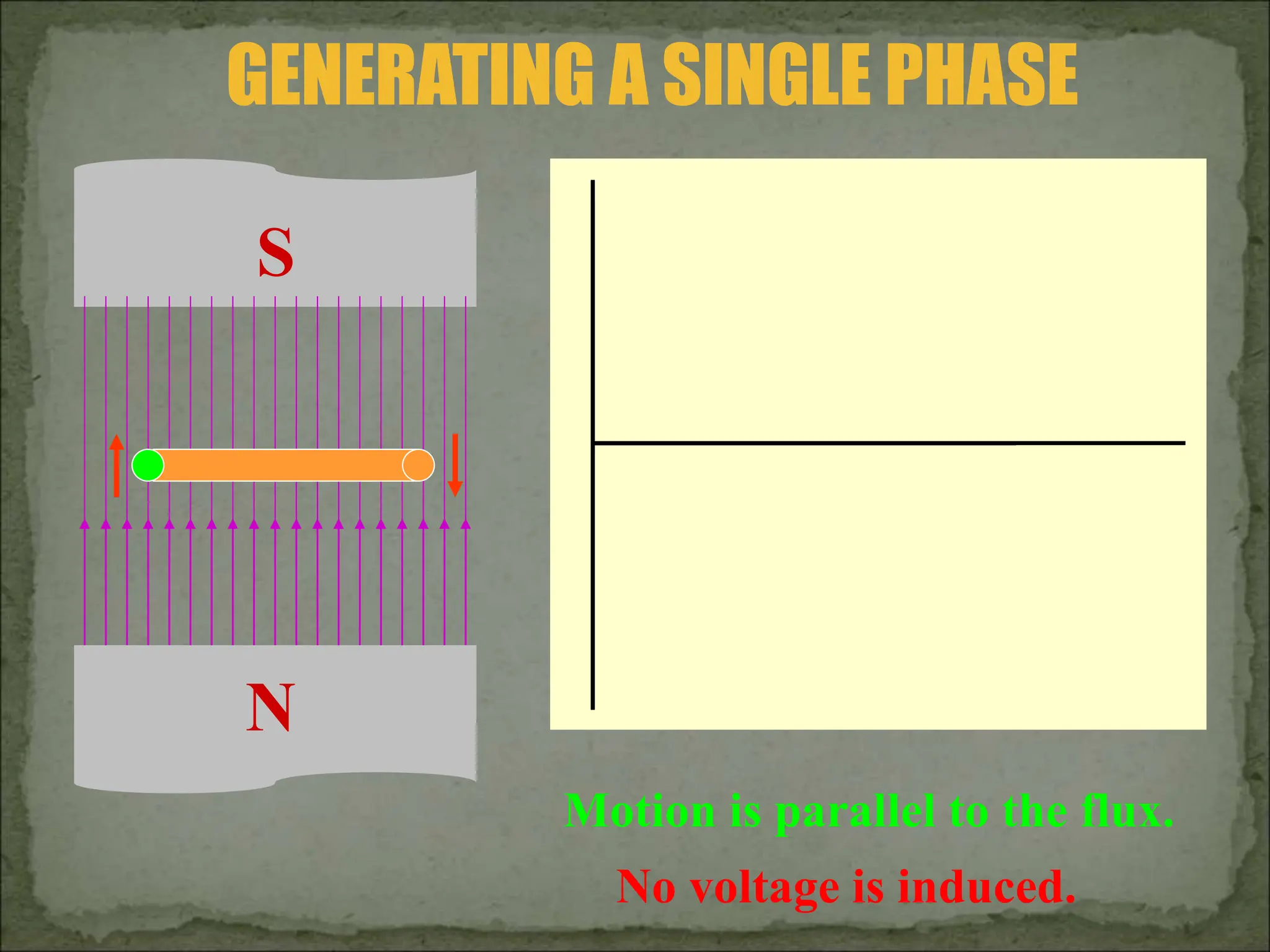
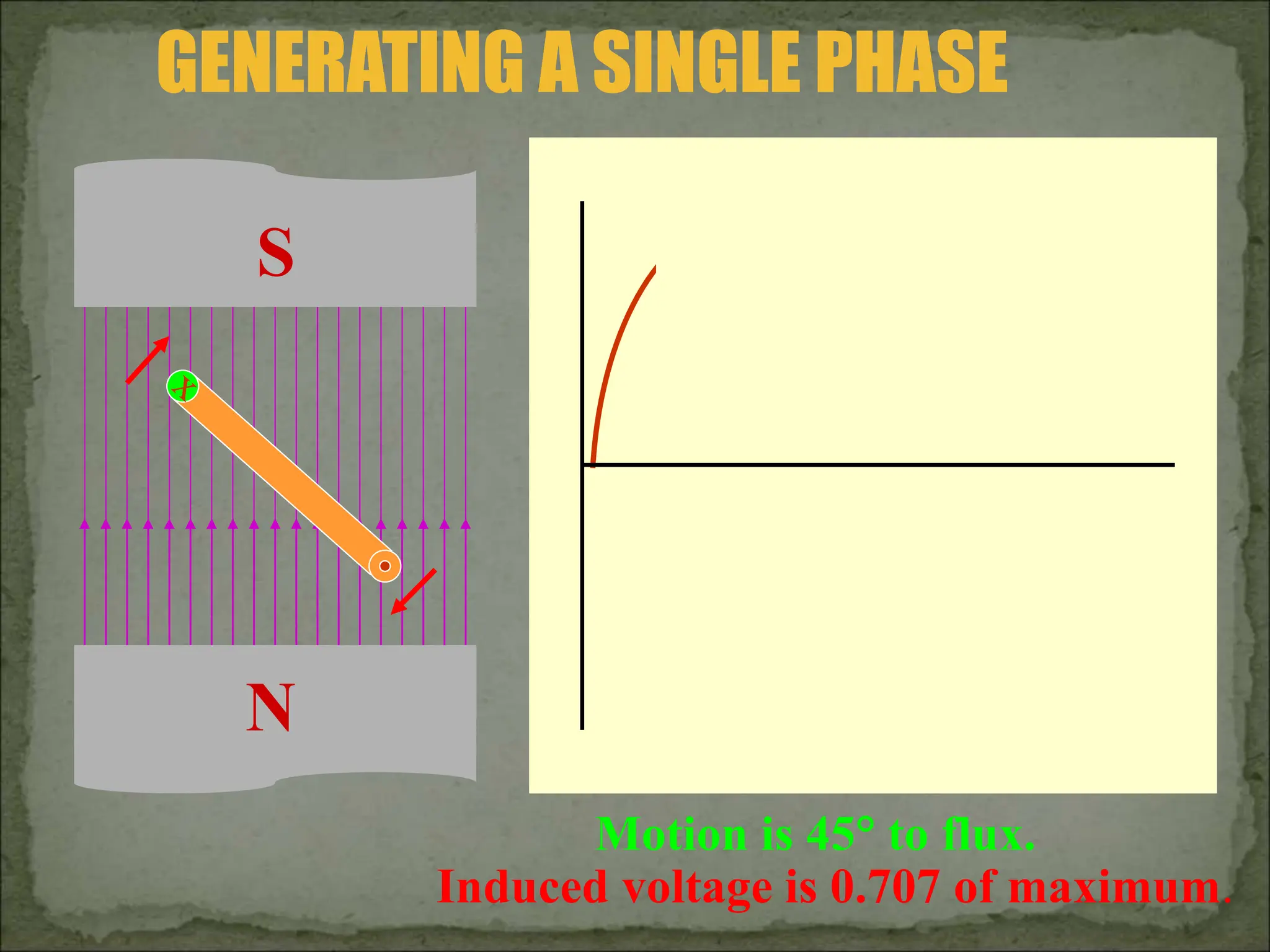
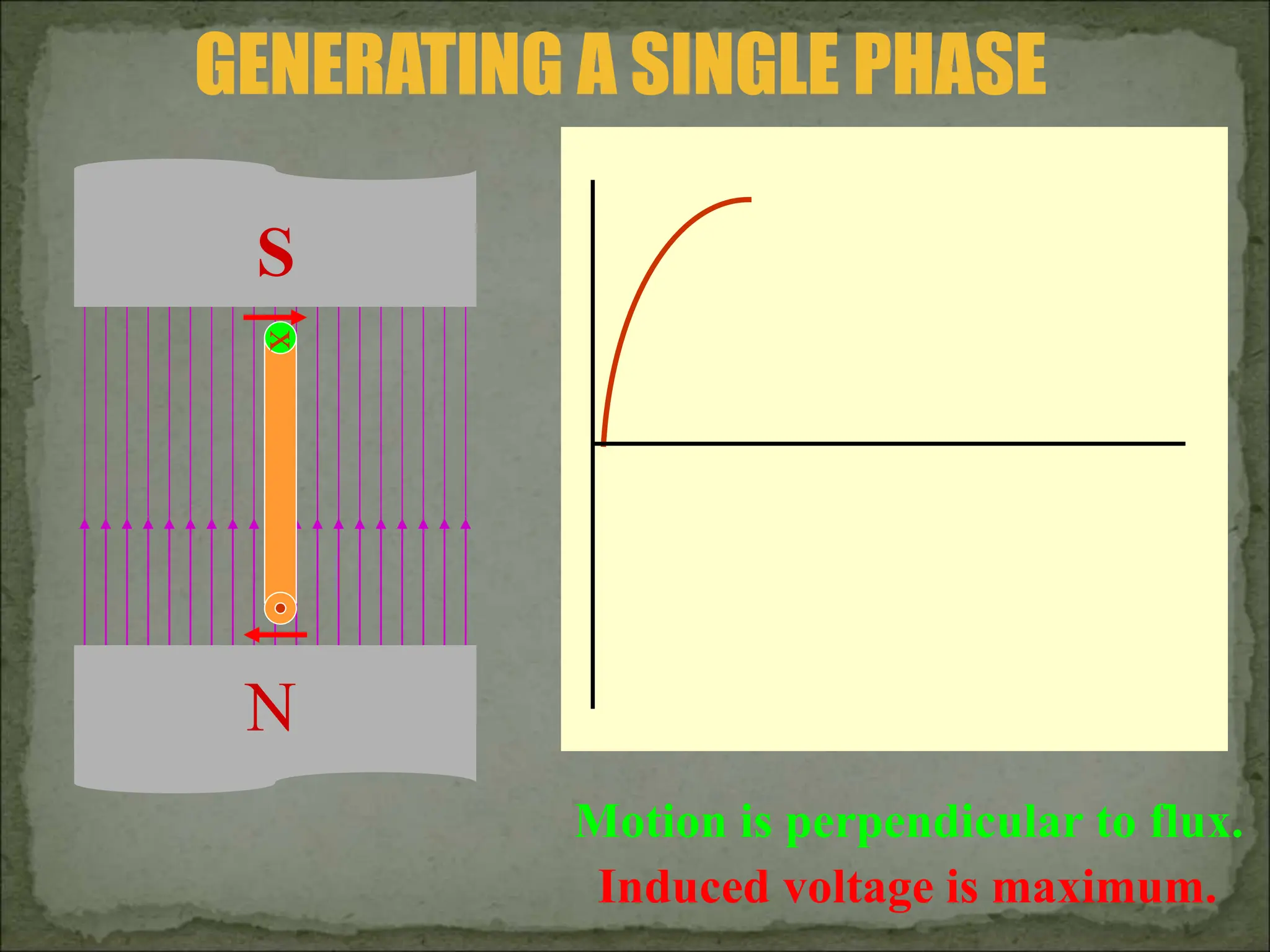
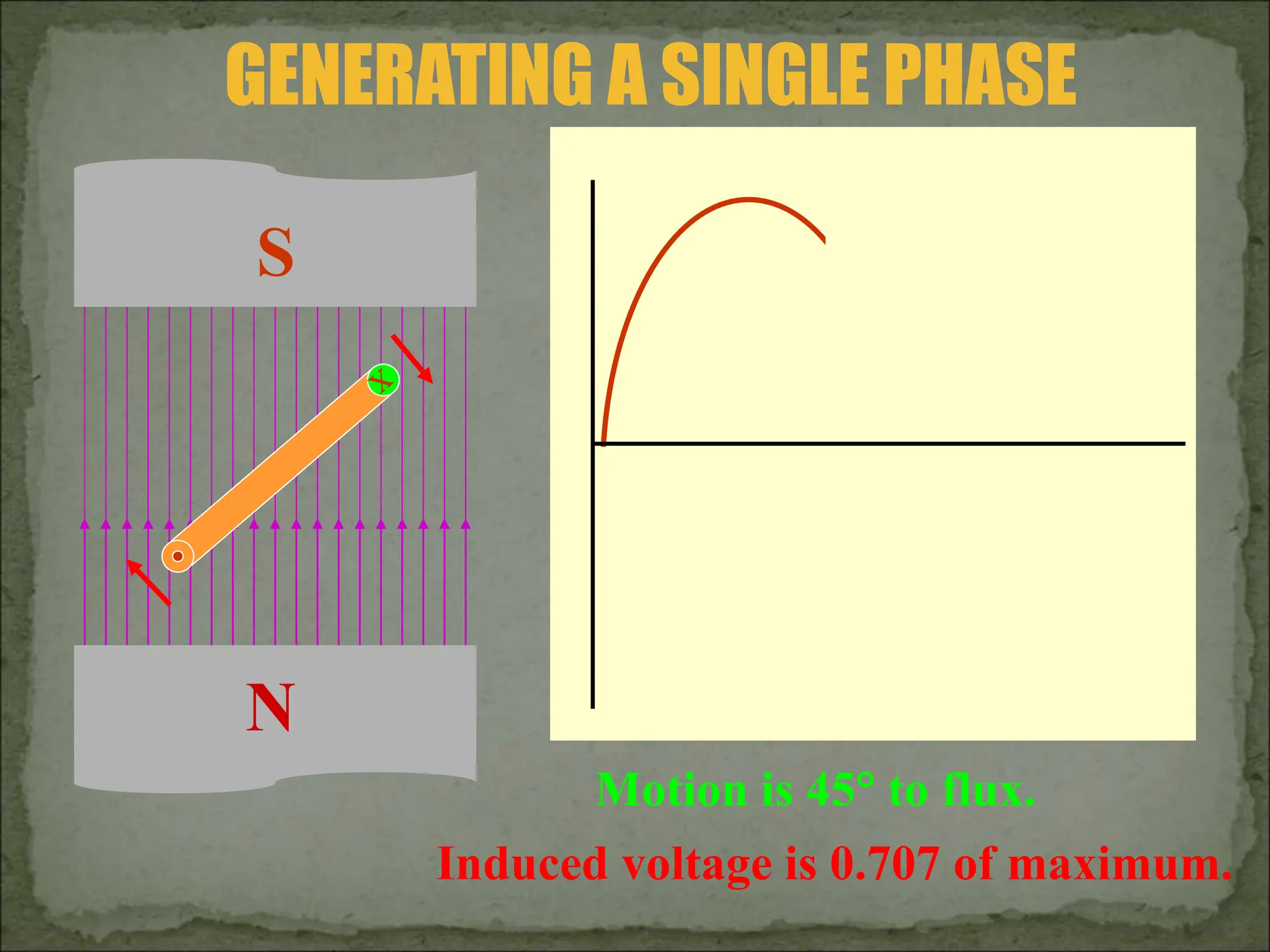
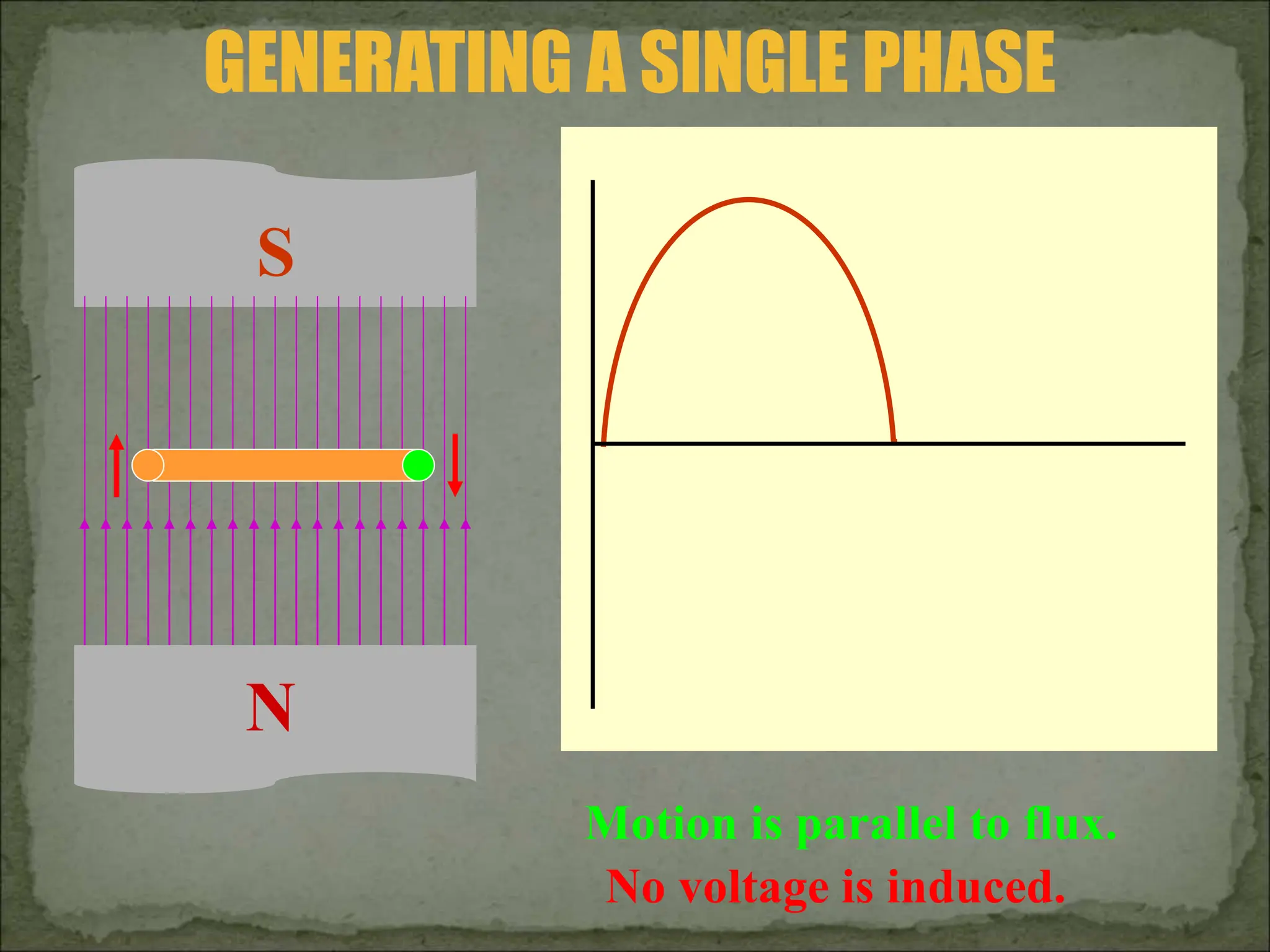
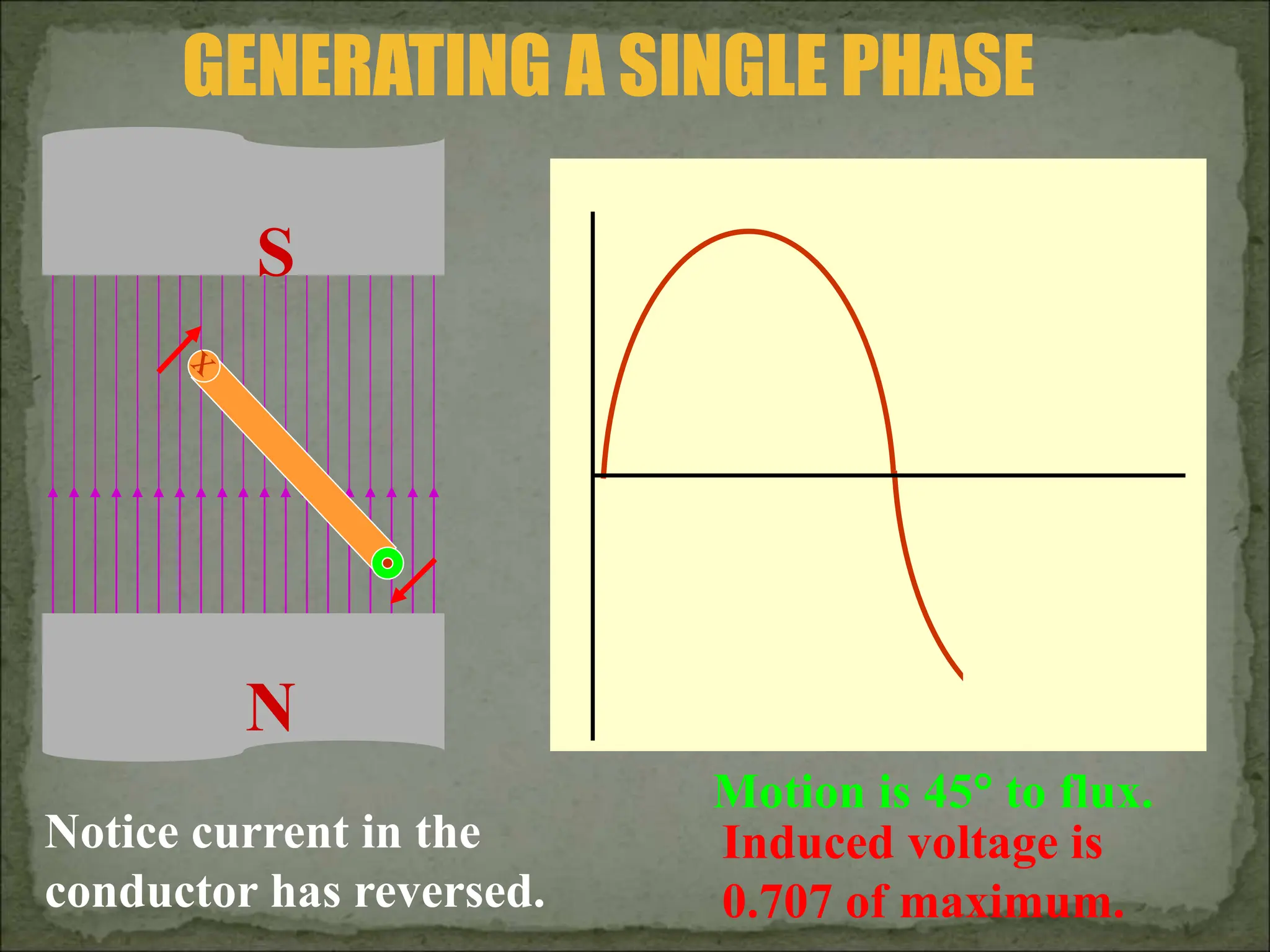
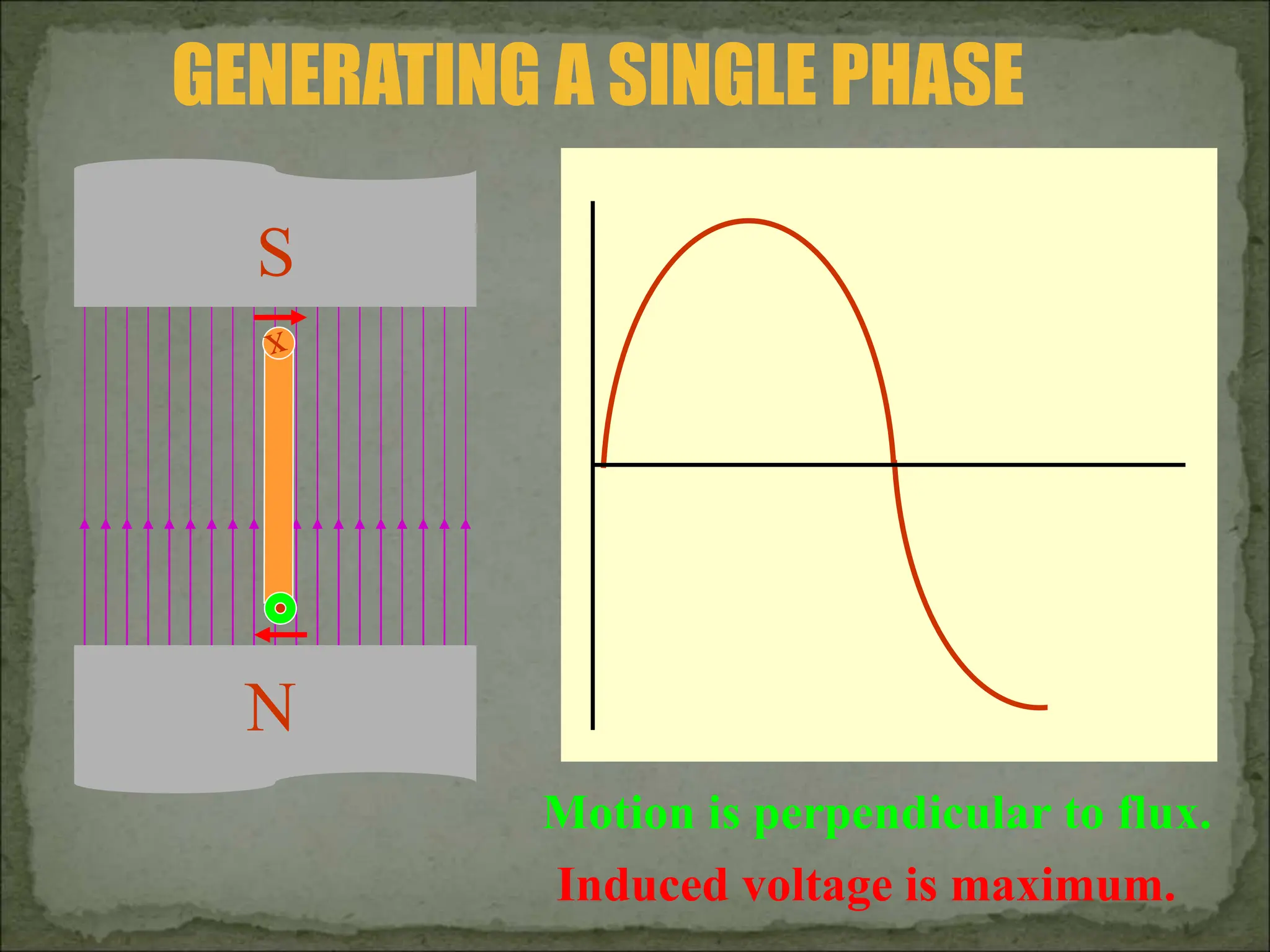
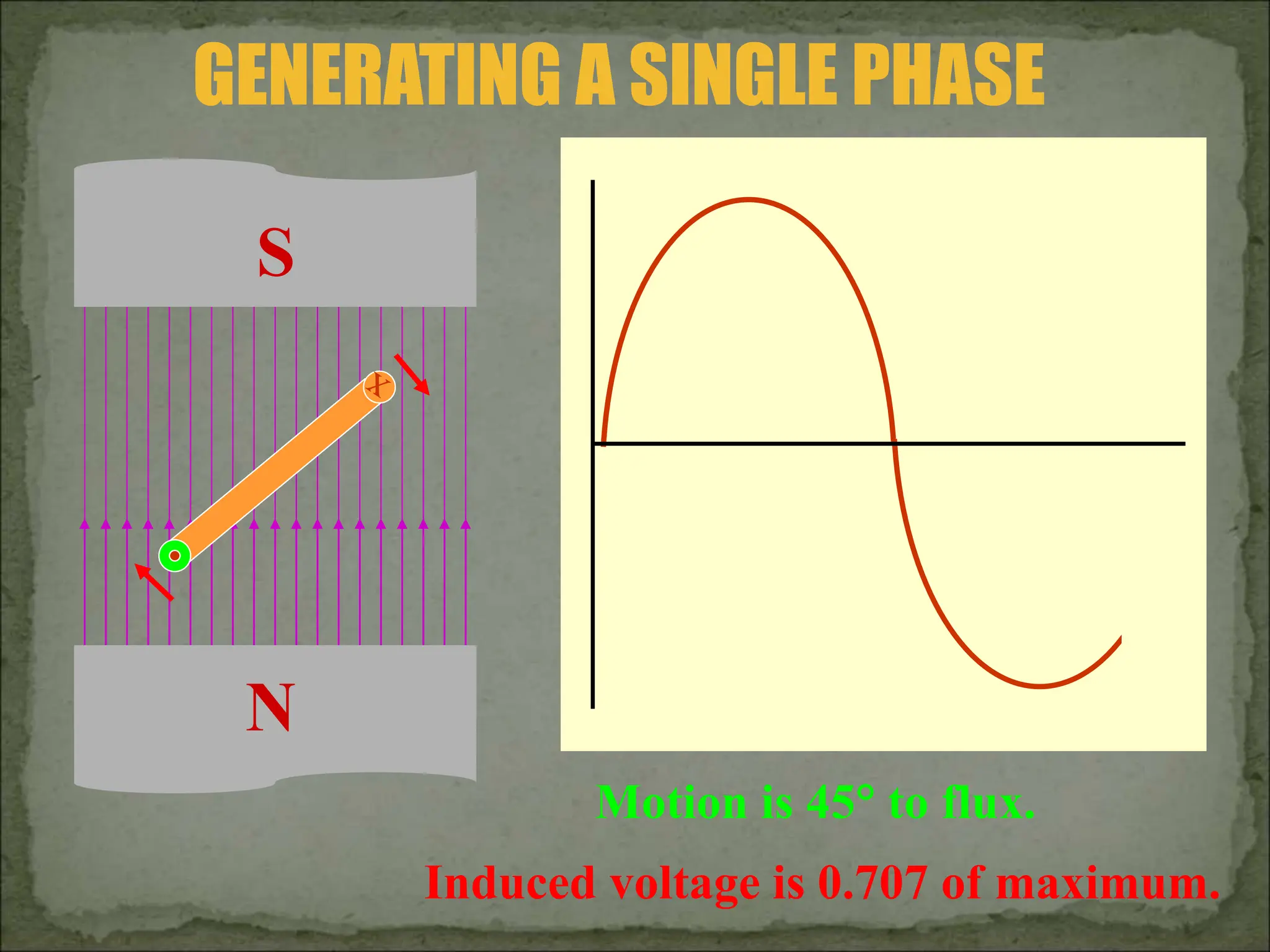
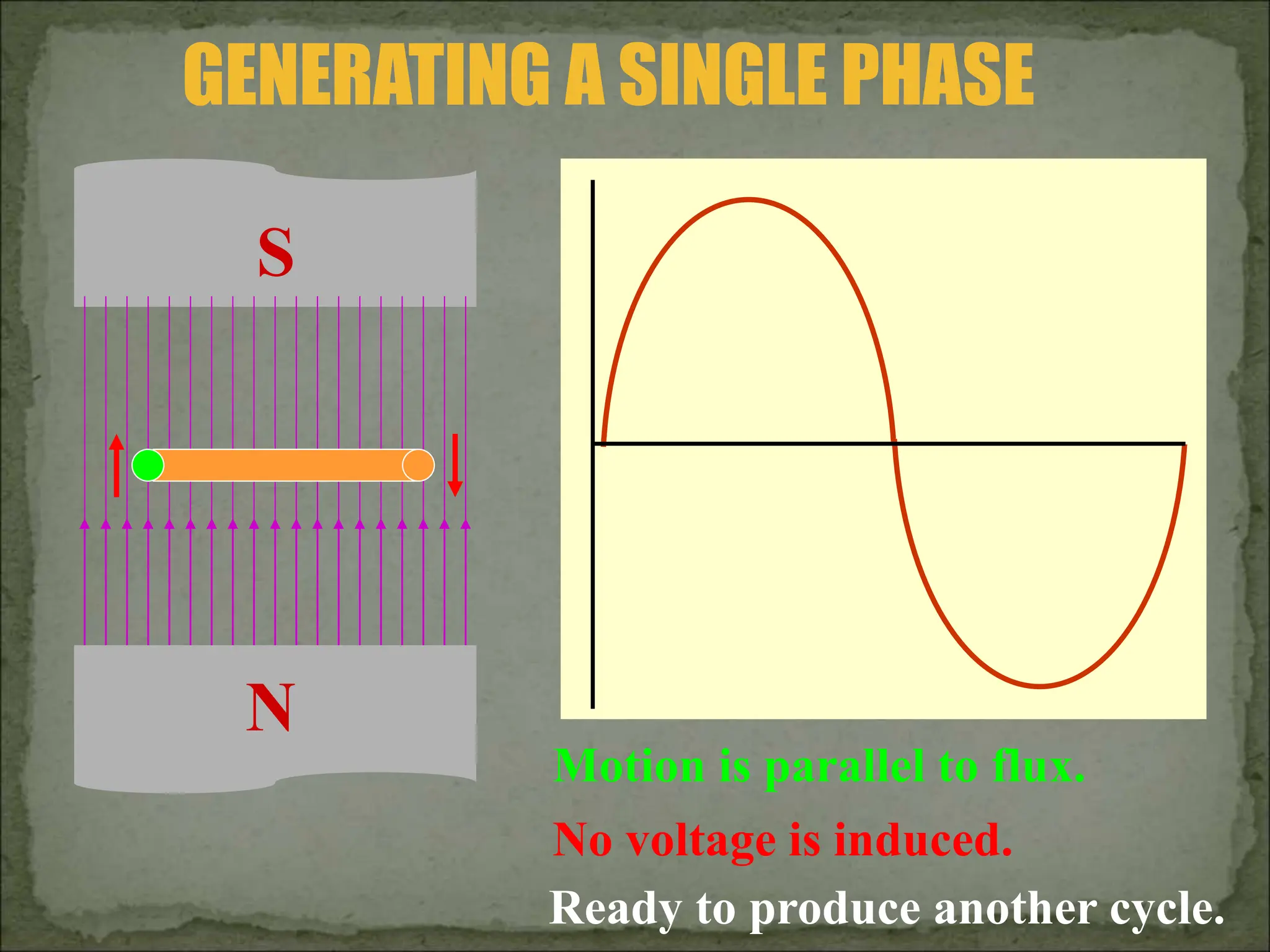
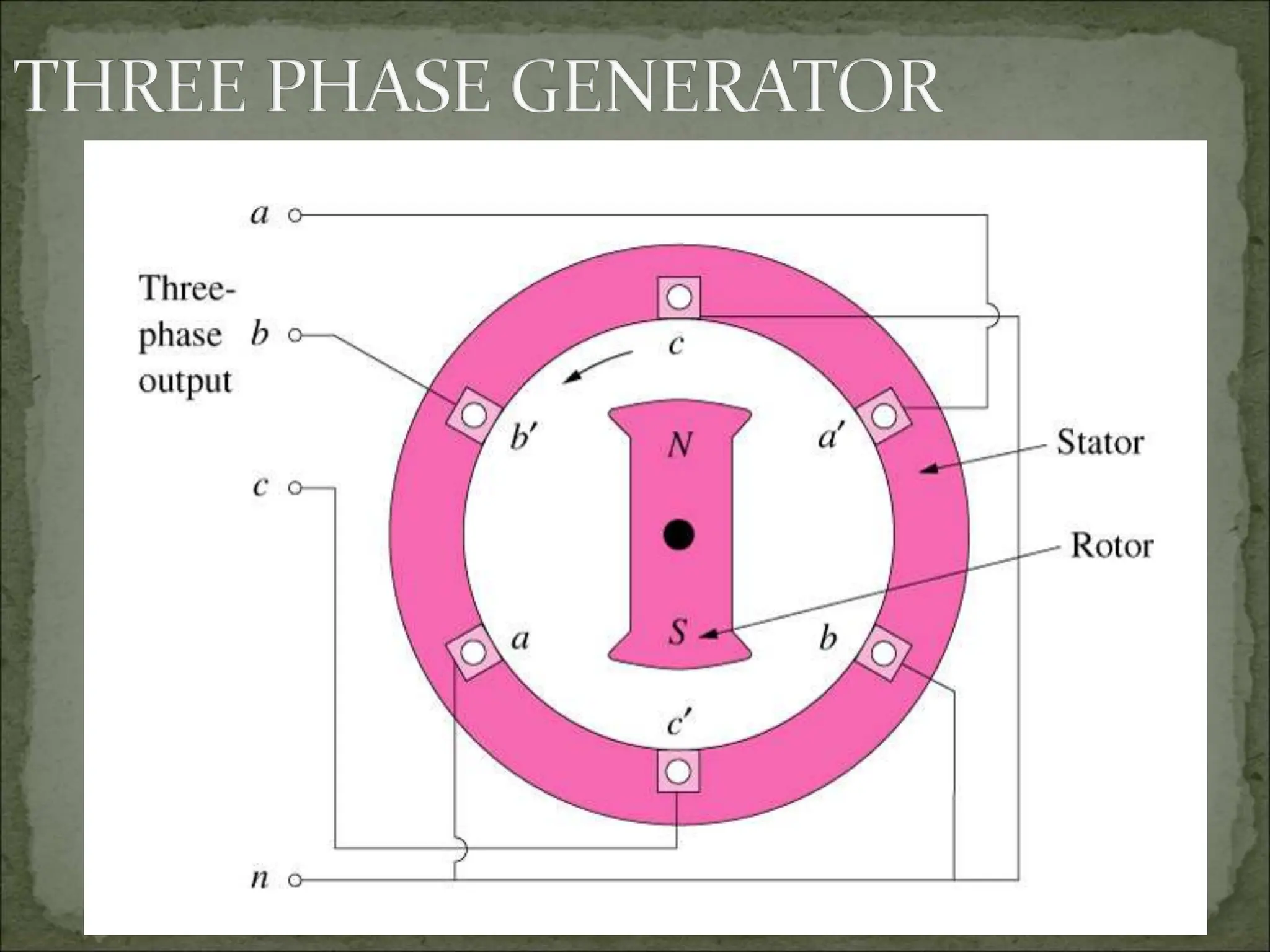
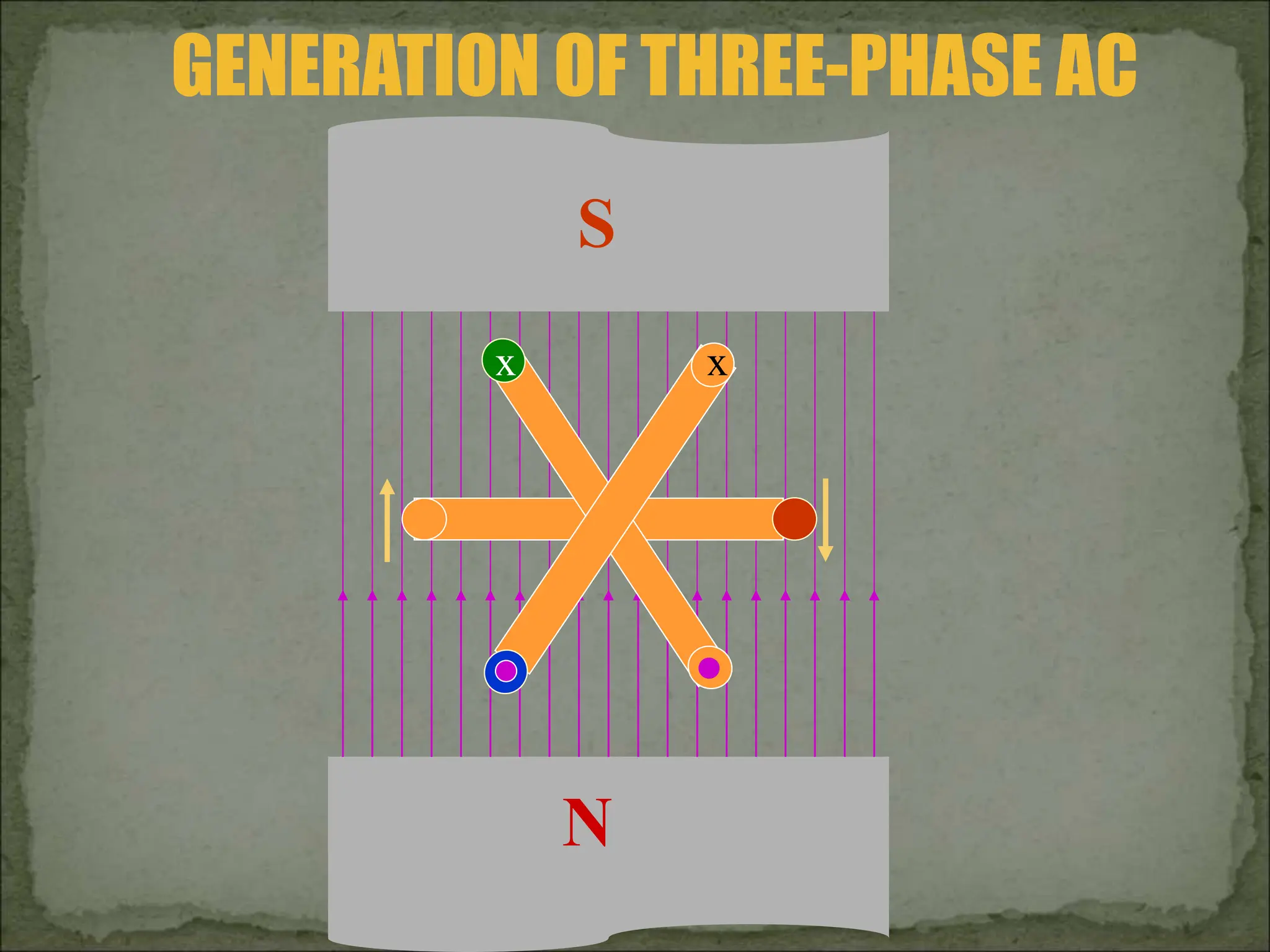
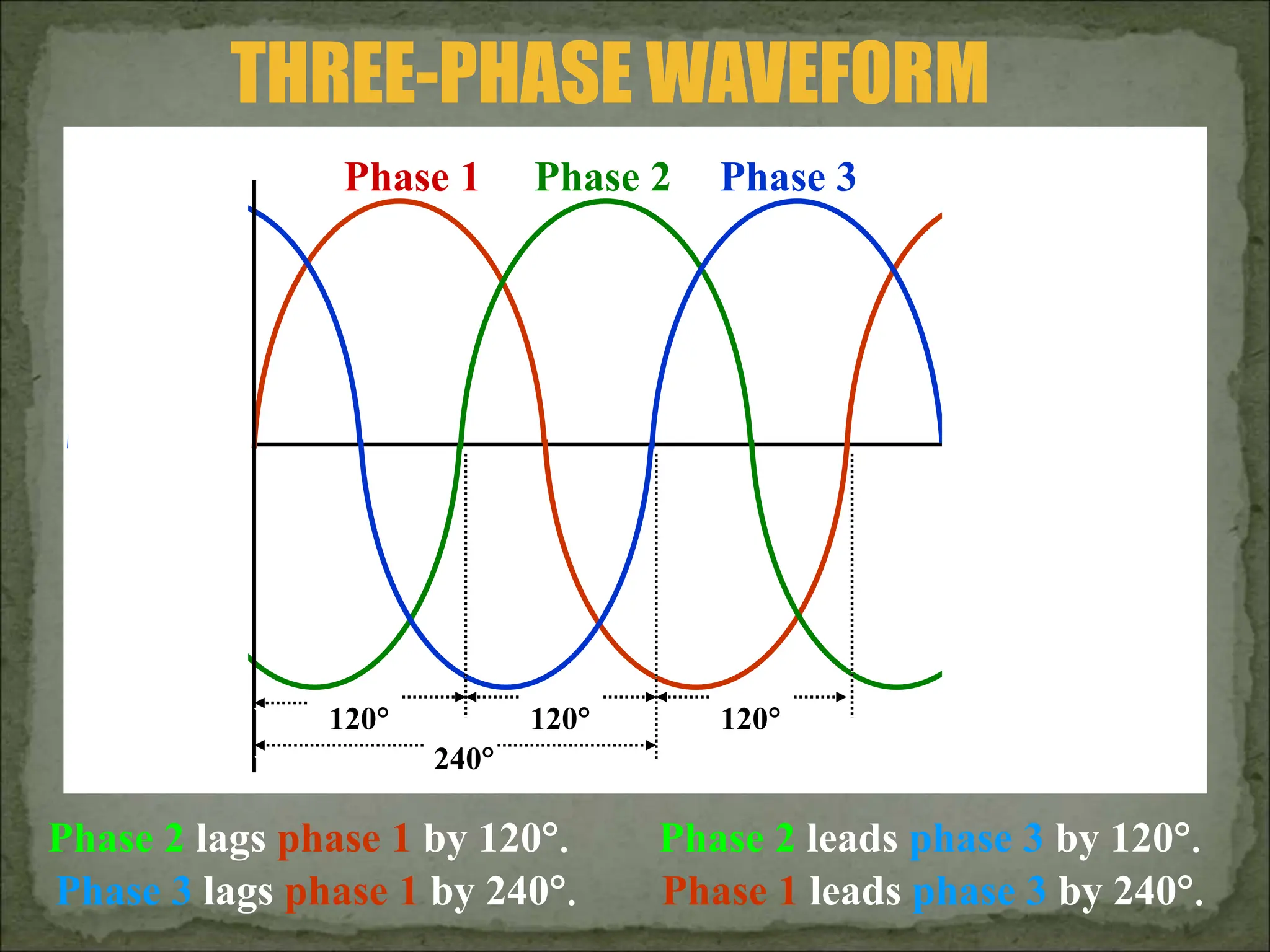
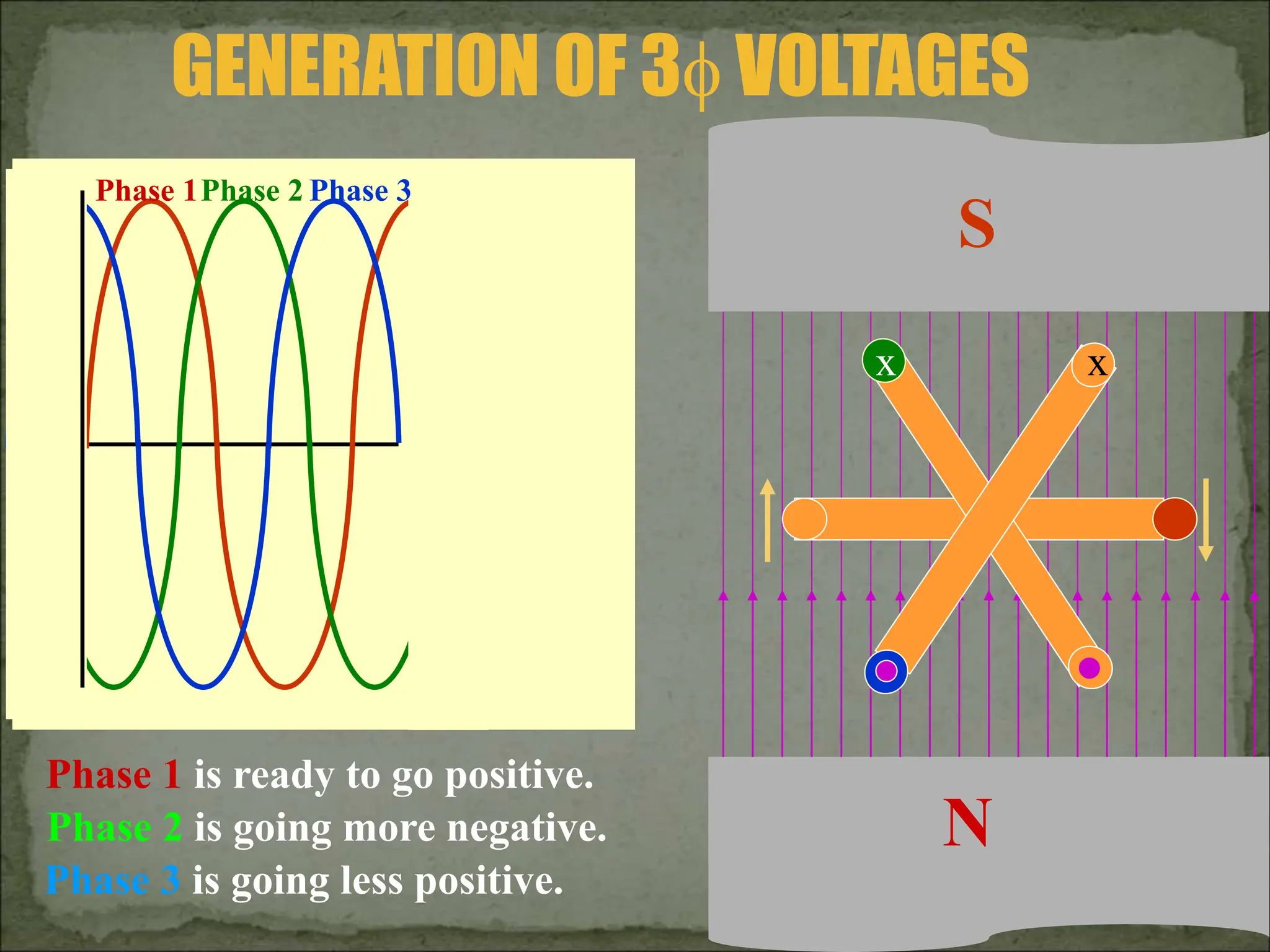
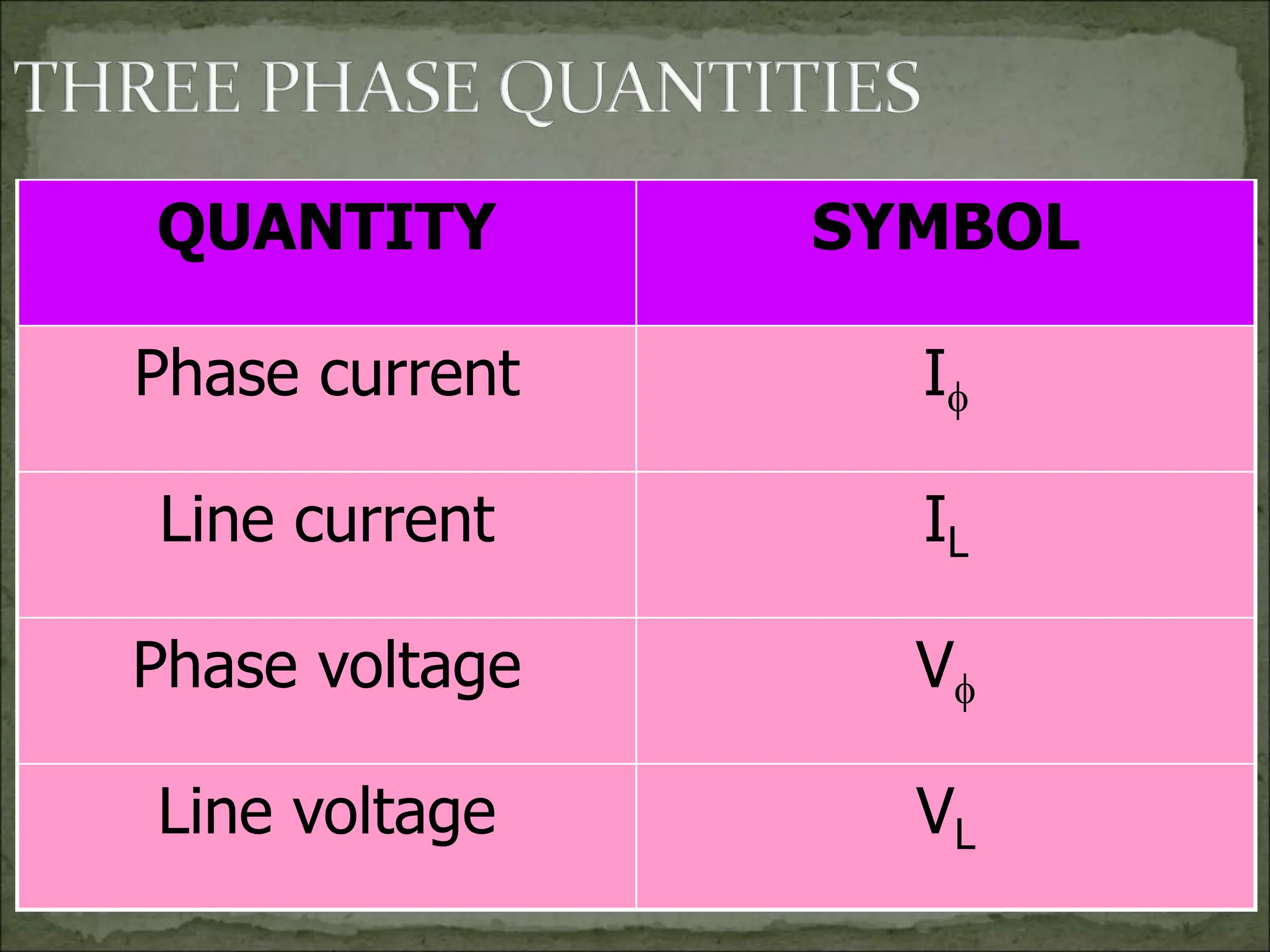
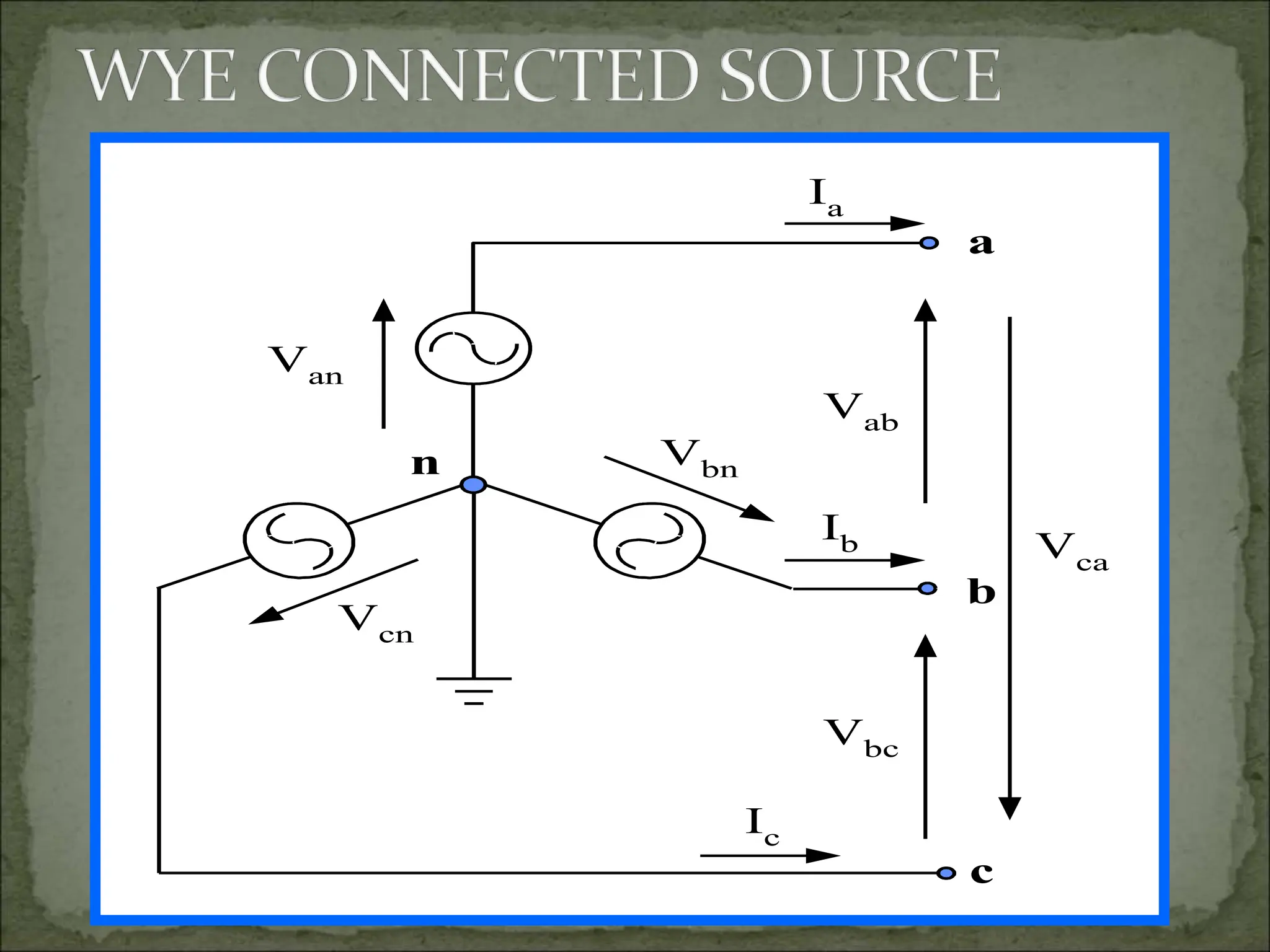
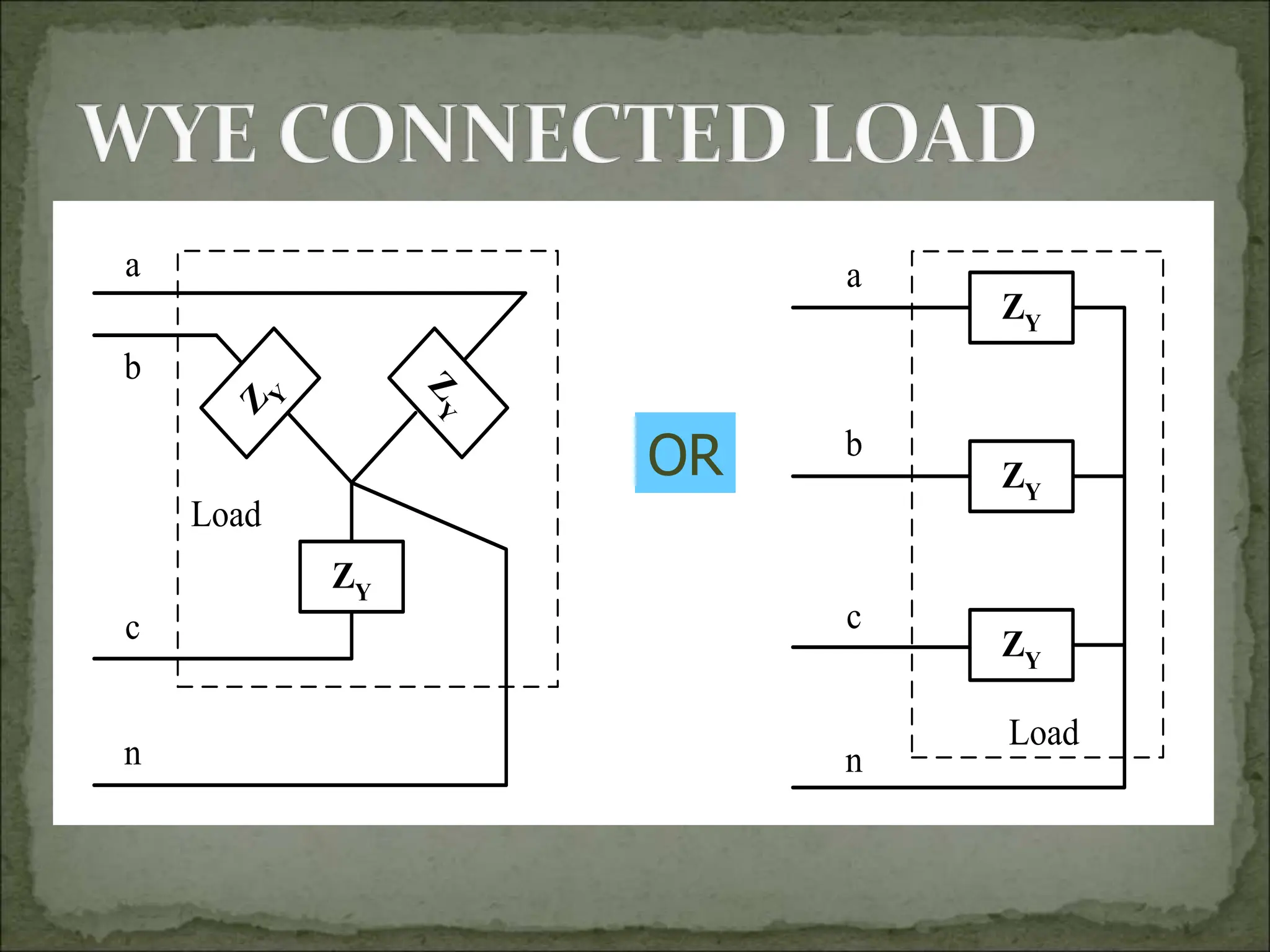
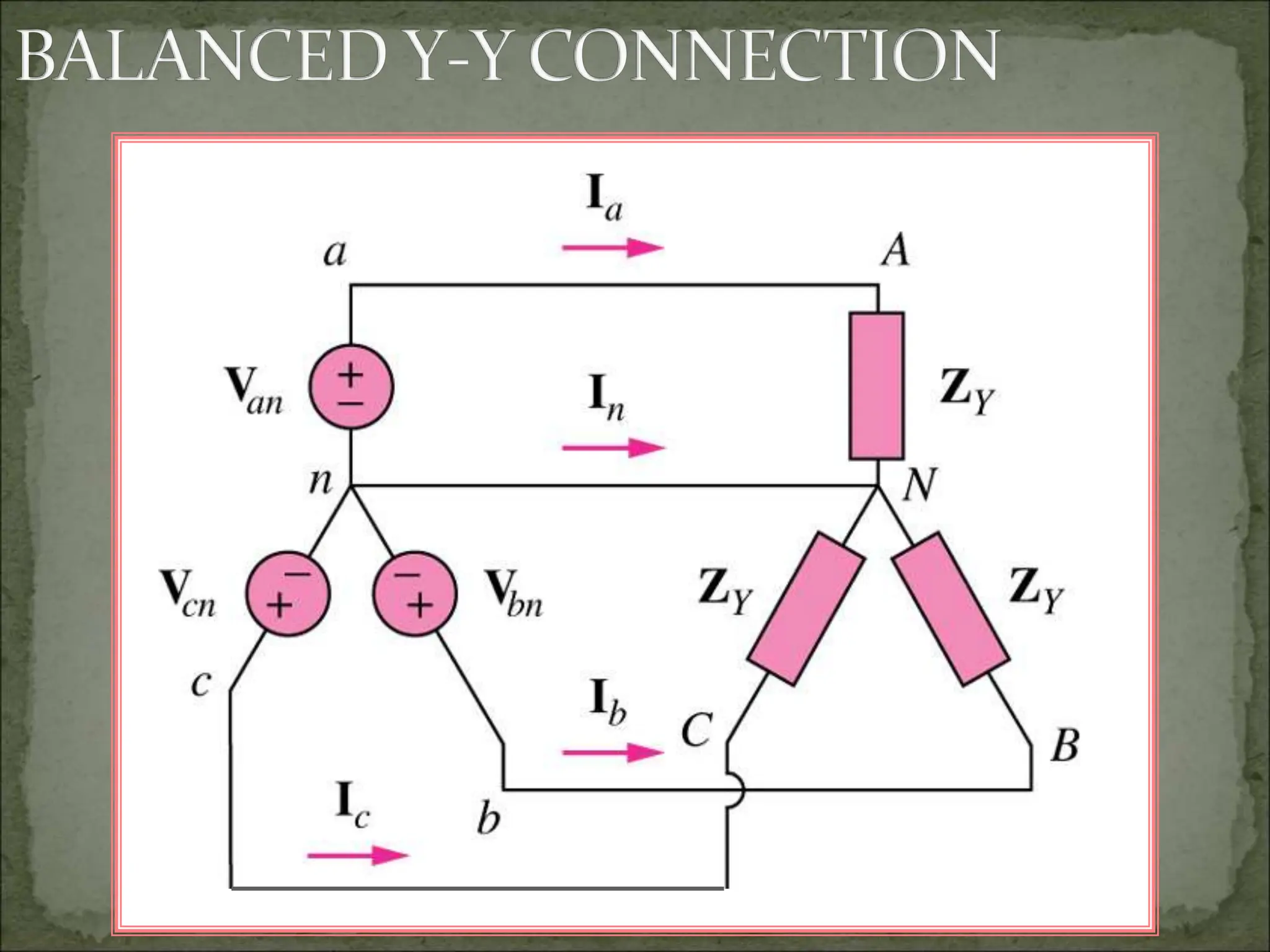
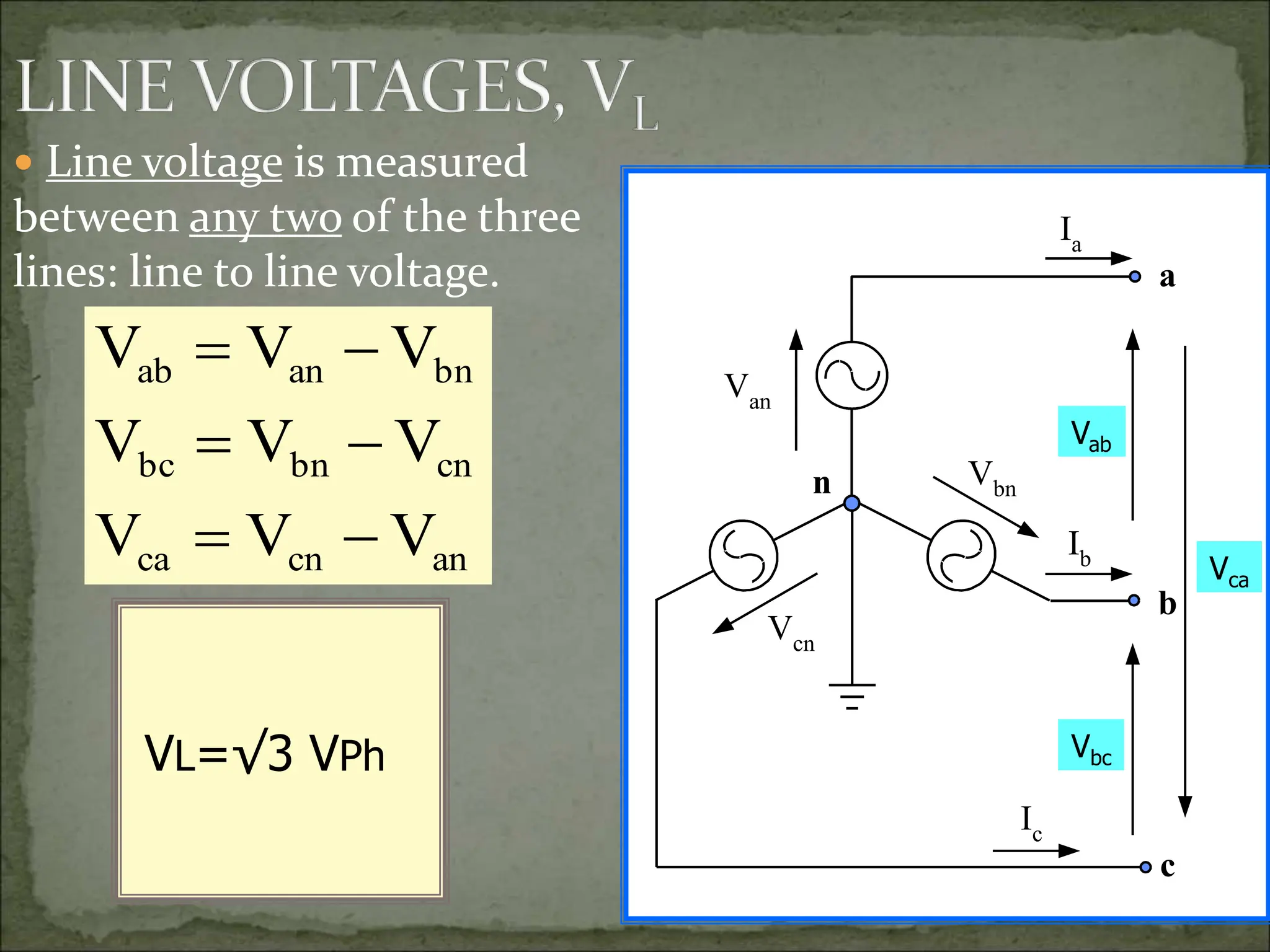
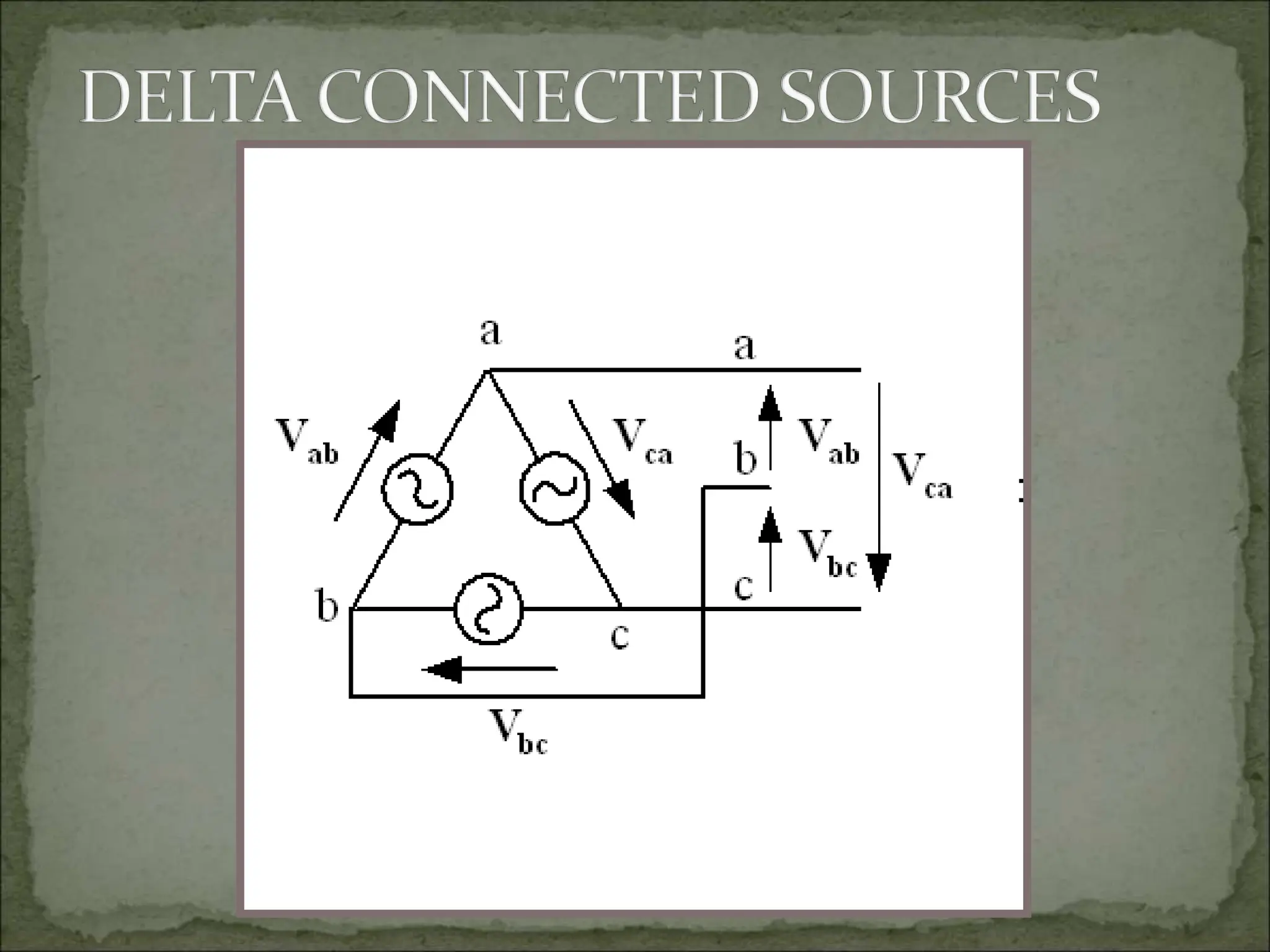
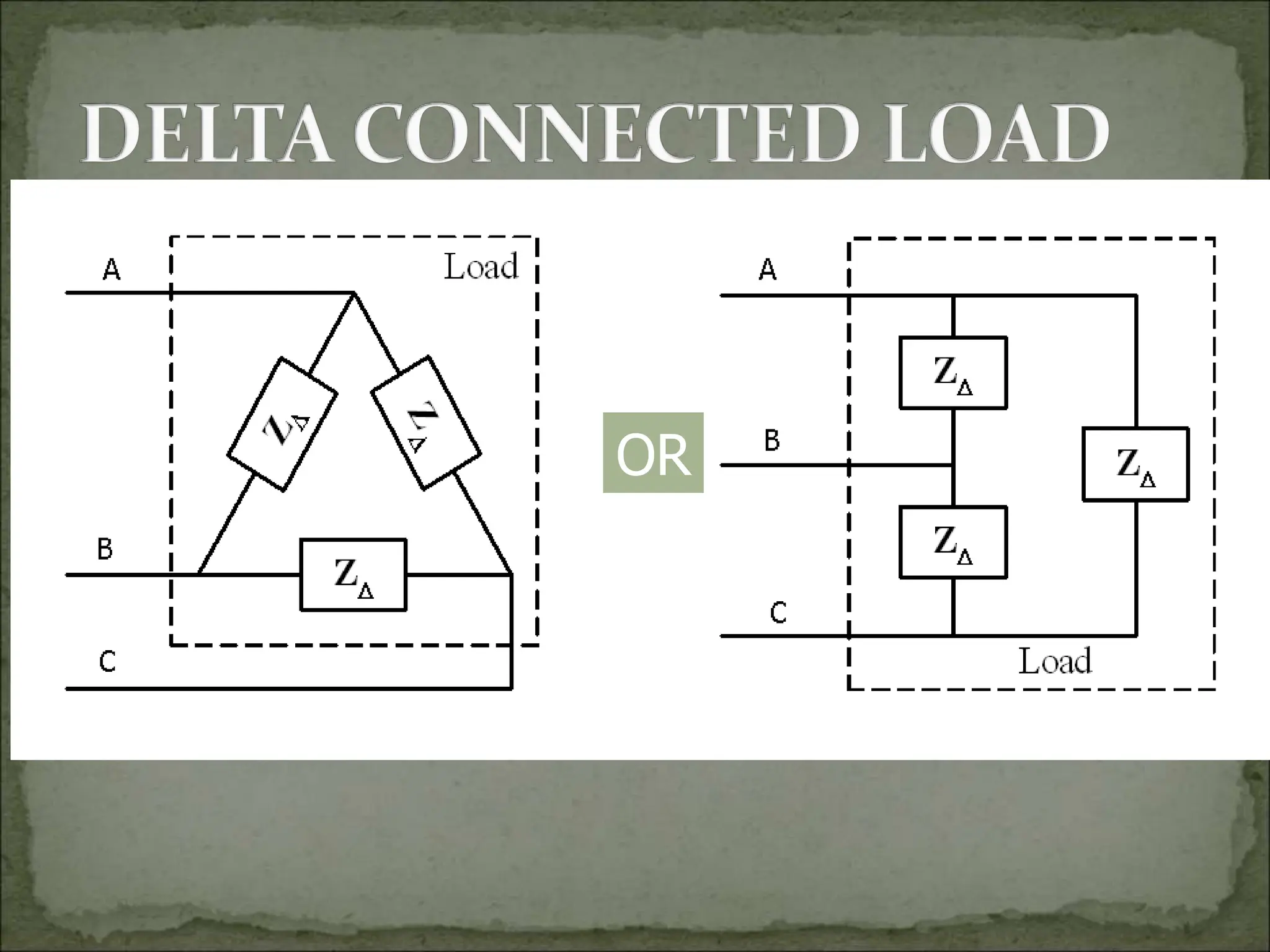
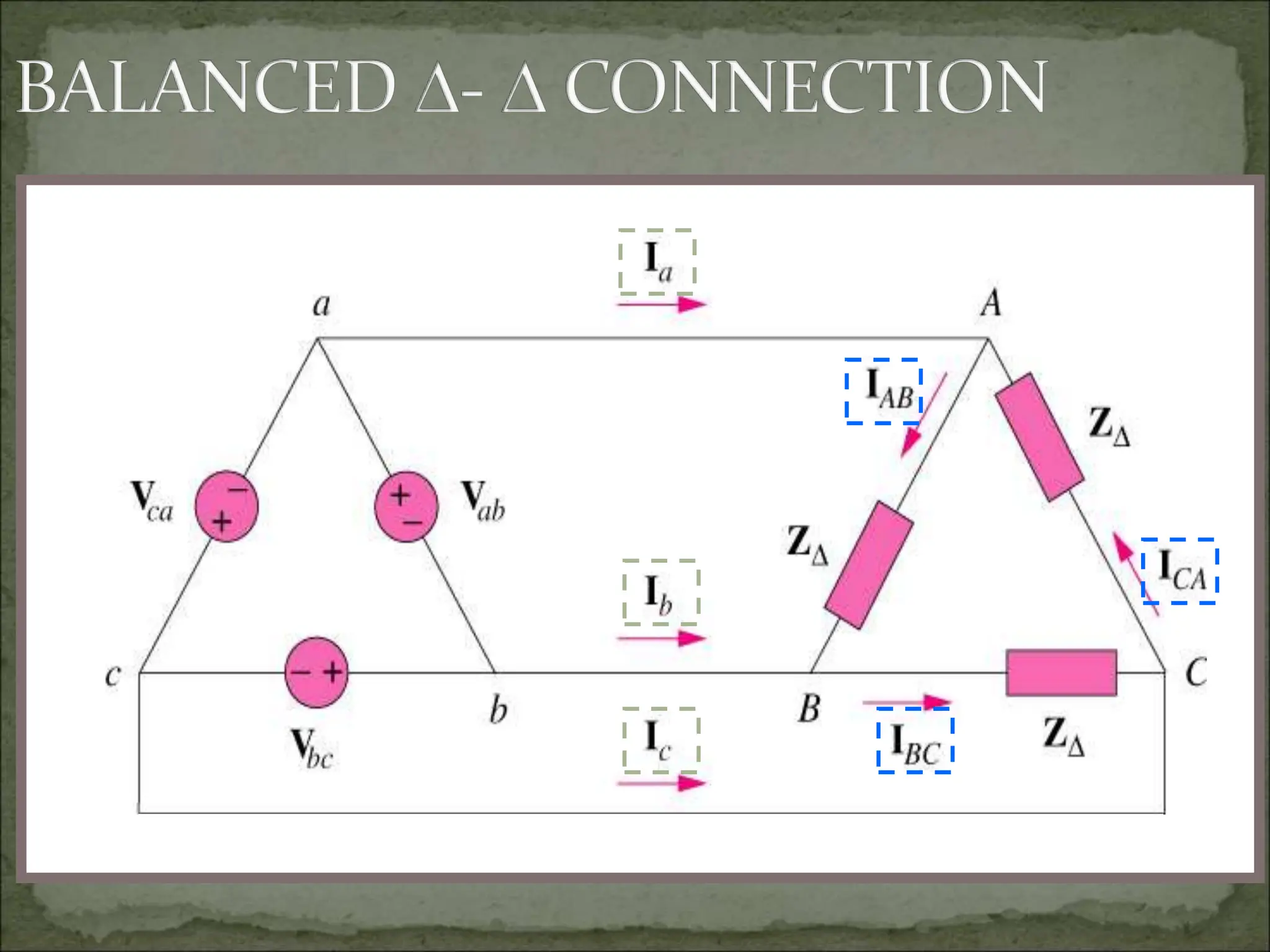
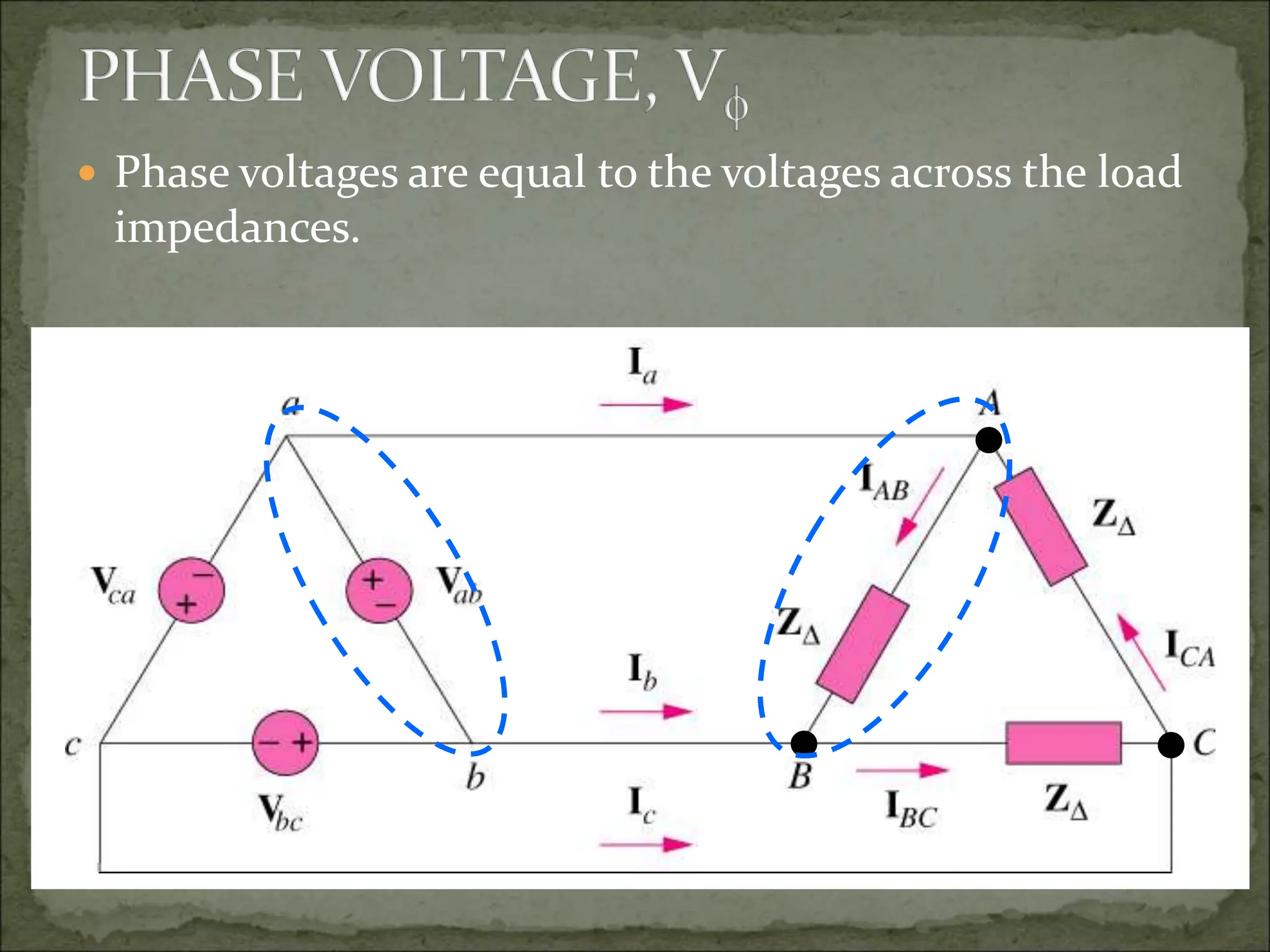
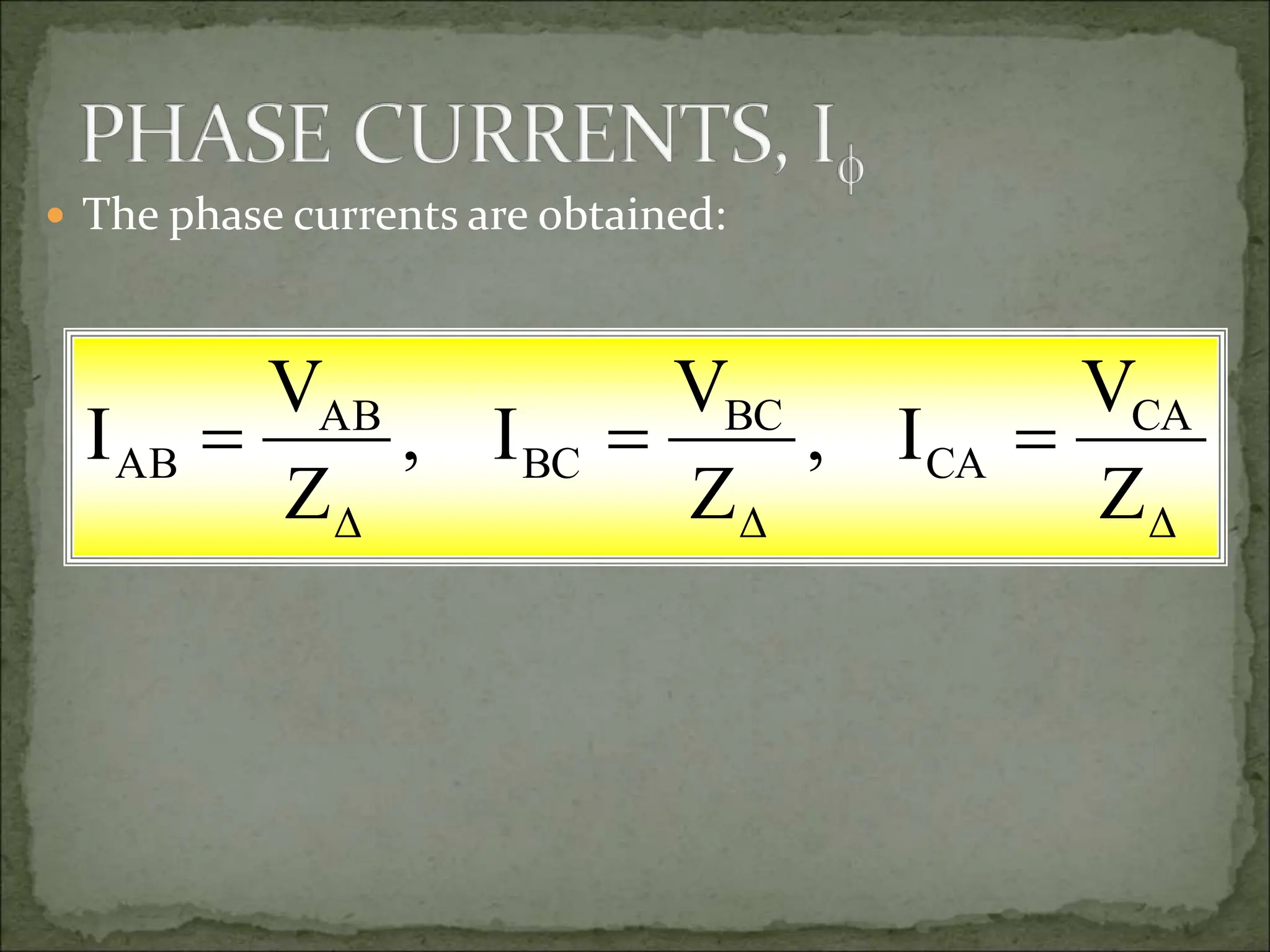
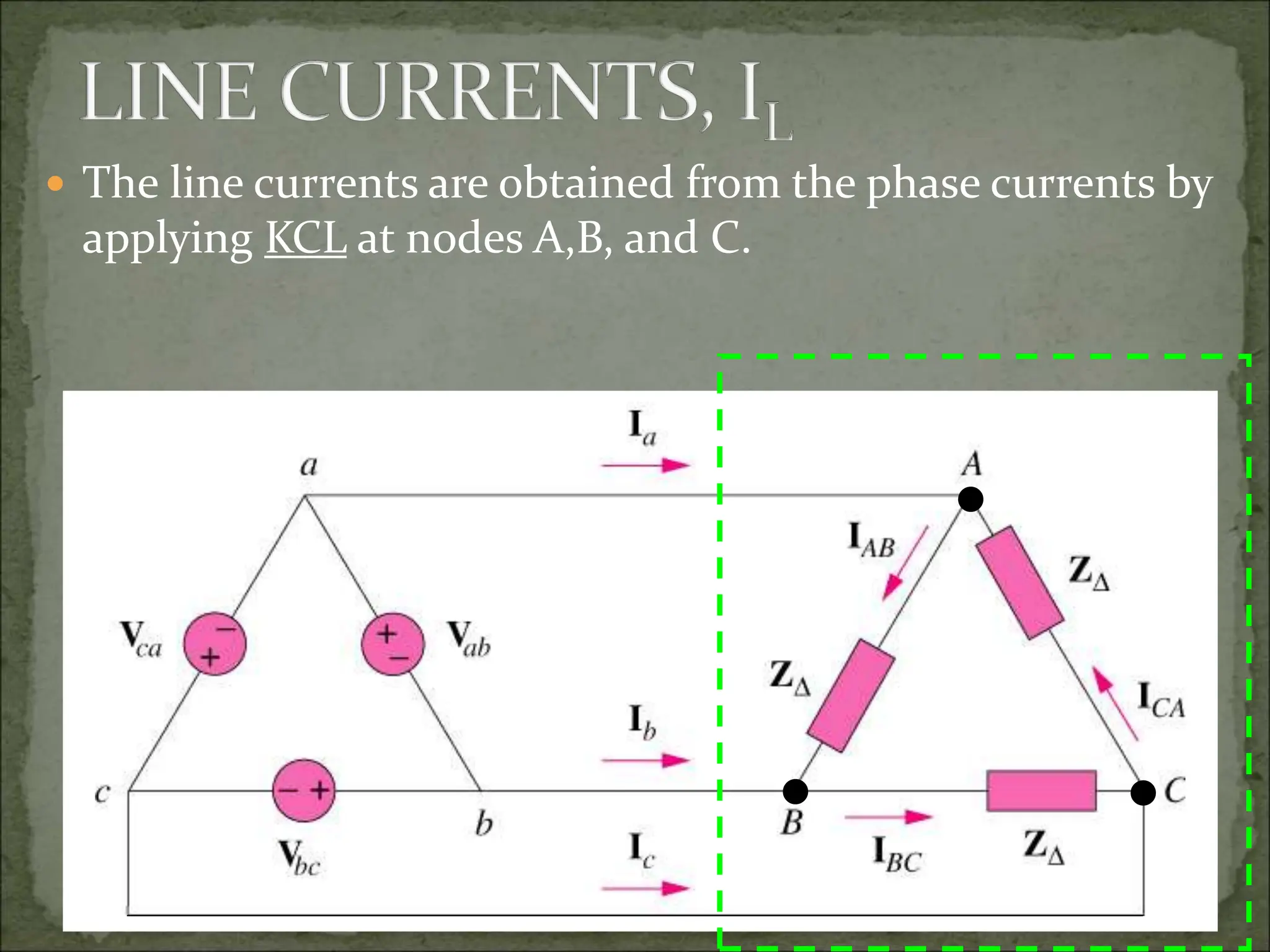
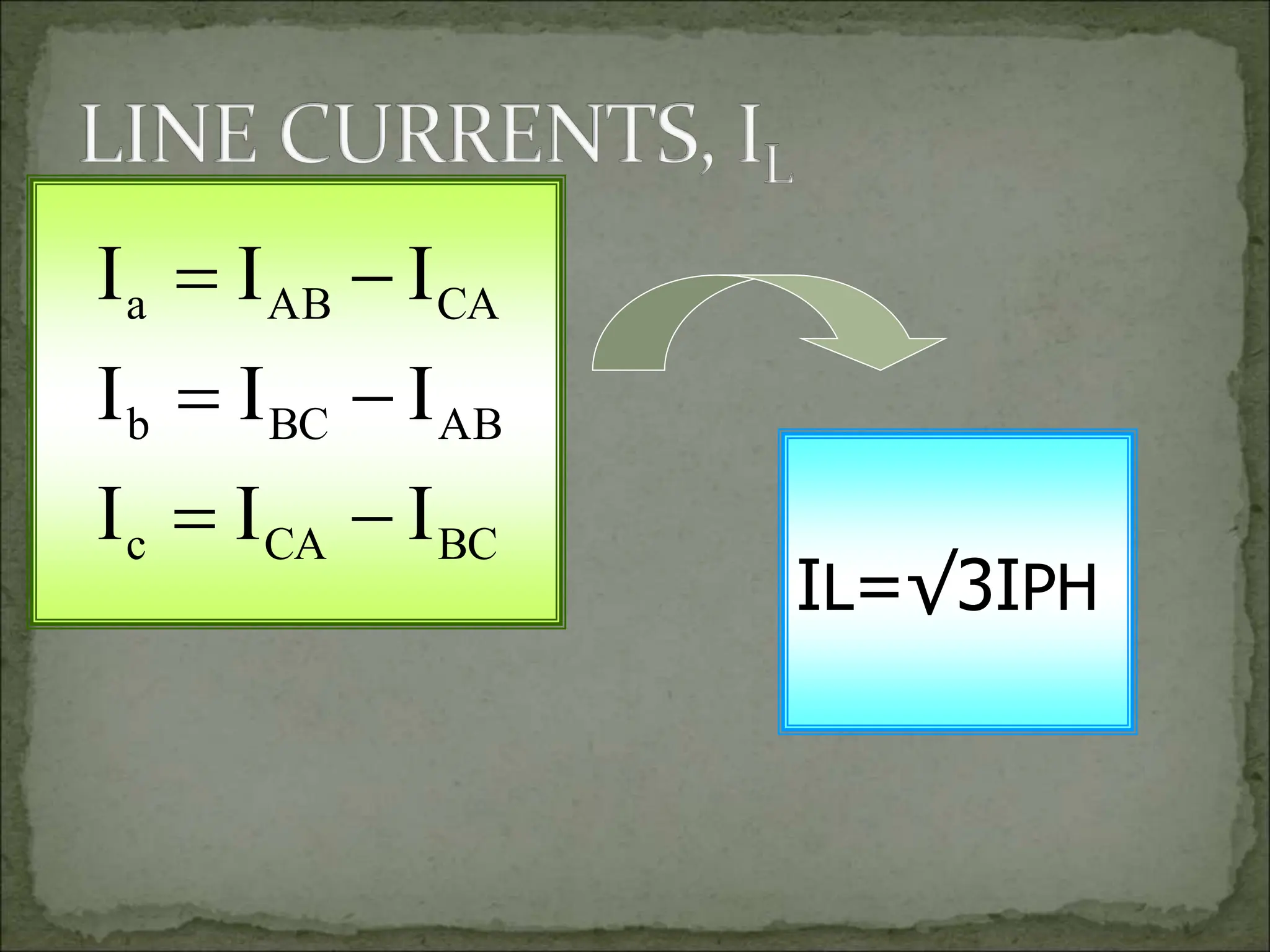
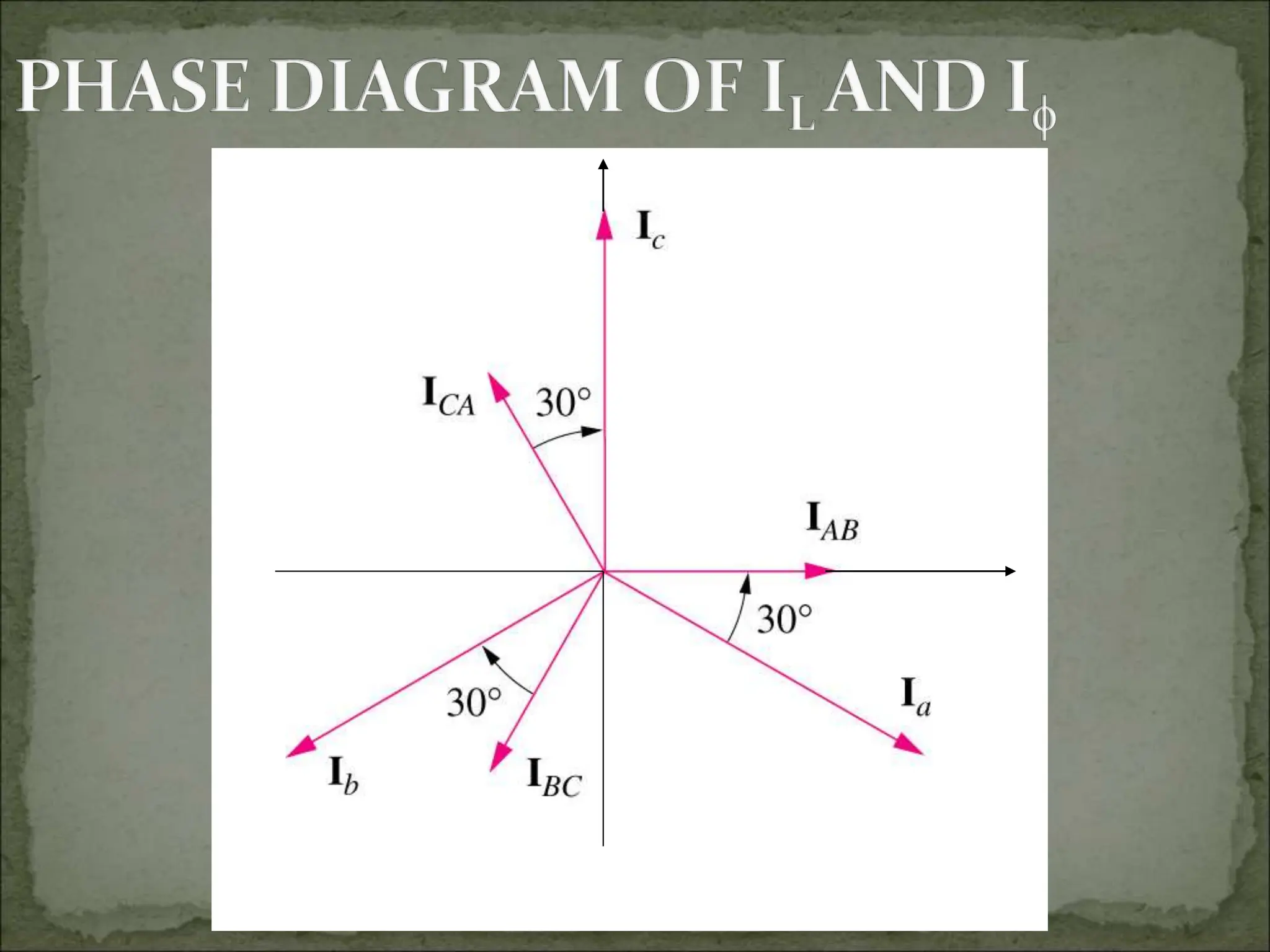
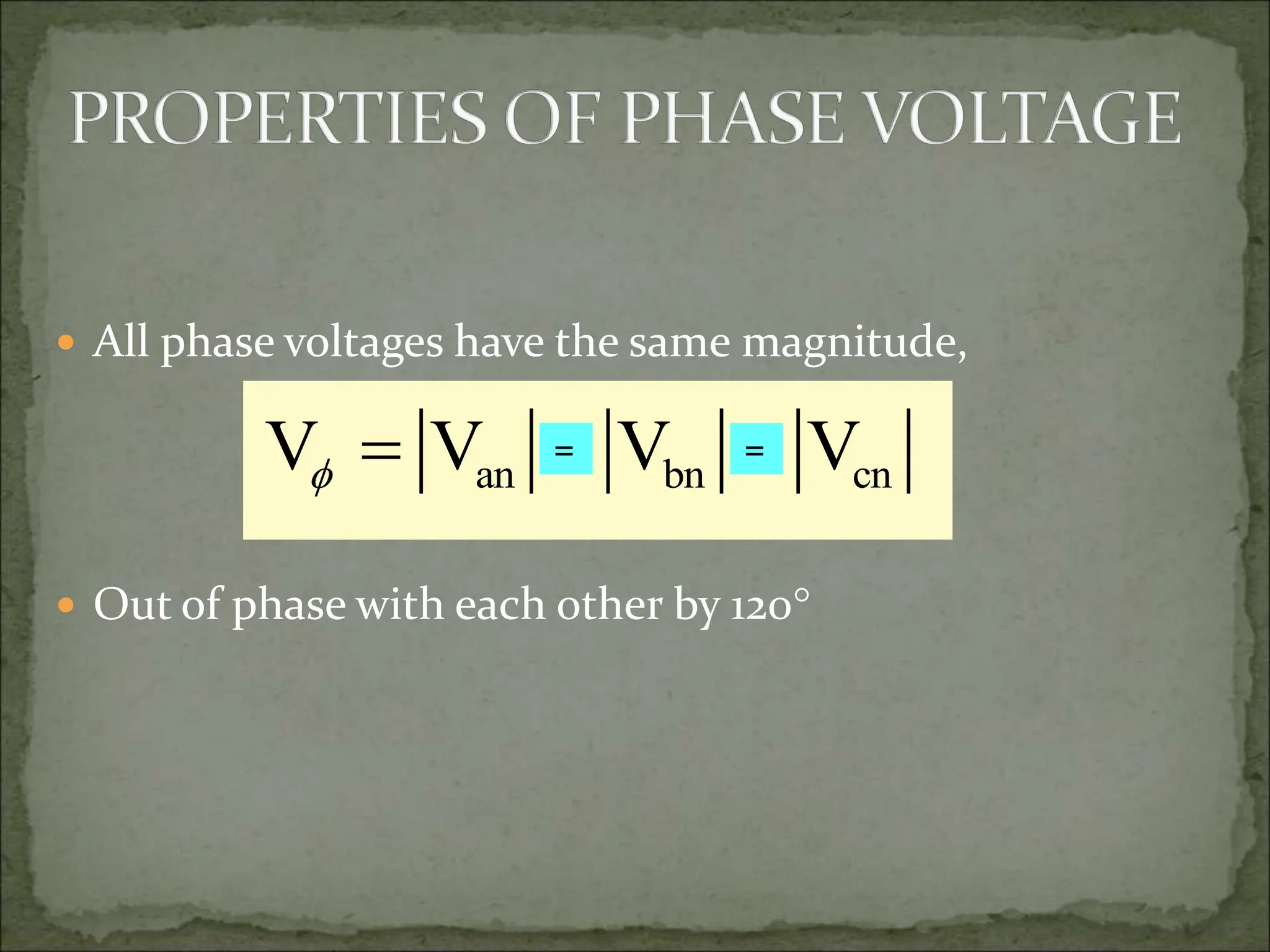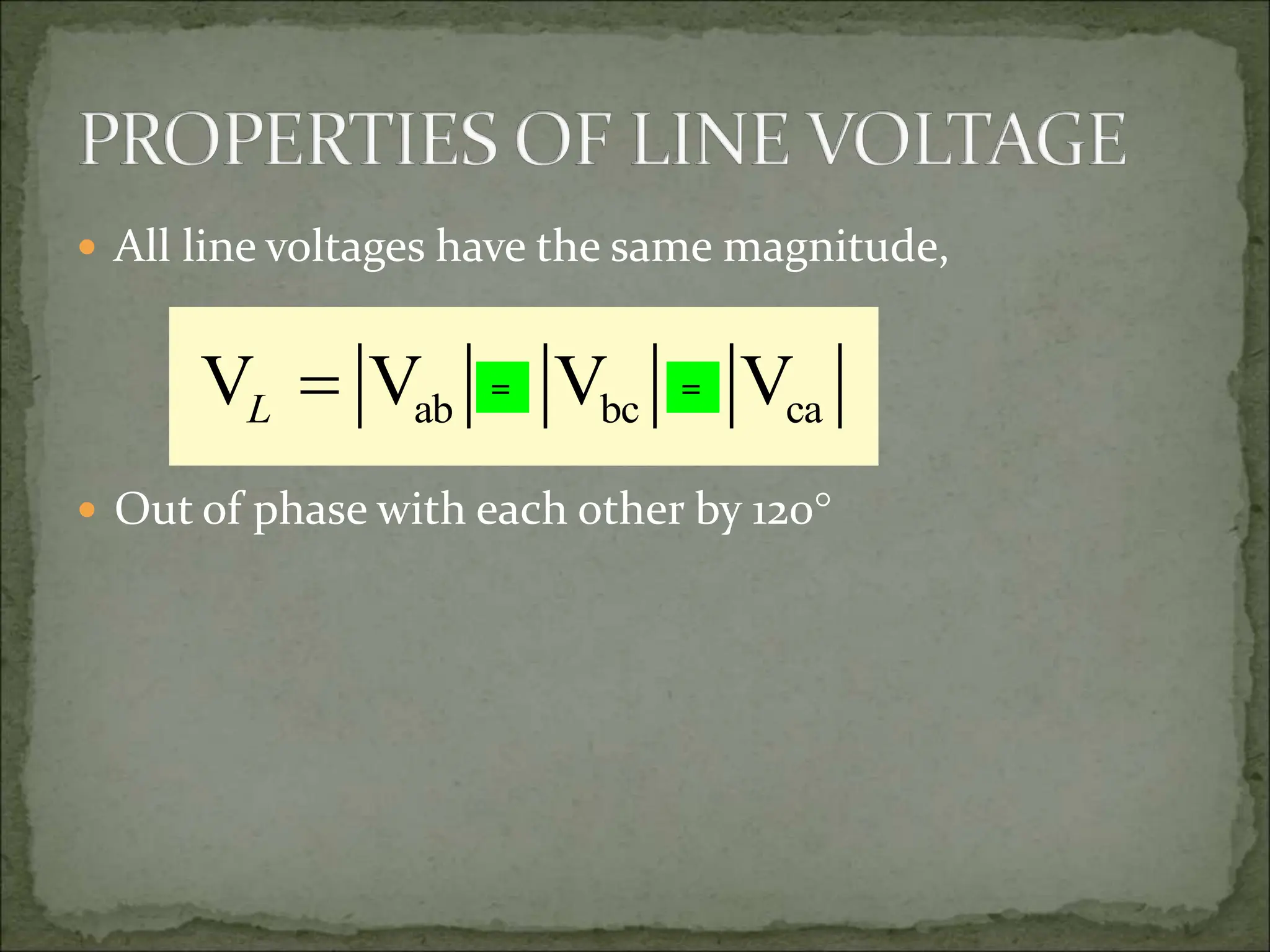This document discusses different types of polyphase systems for generating and supplying alternating current (AC). It describes single phase, two phase, and three phase systems. In a three phase system, a generator contains three coils placed 120 degrees apart that generate three voltages equal in magnitude but out of phase by 120 degrees. Common connections of three phase systems include wye-wye, wye-delta, delta-delta, and delta-wye. Phase and line quantities are also defined.

1.  A generator connected through a pair of wire to a load –
Single Phase Two Wire.
 Vp is the magnitude of the source voltage, and  is the
phase.


p
V

2. 

p
V


p
V
 Most common in
practice: two
identical sources
connected to two
loads by two outer
wires and the
neutral: Single
Phase Three
Wire.
 Terminal voltages
have same
magnitude and
the same phase.

3. Circuit or system in which AC
sources operate at the same
frequency but different phases are
known as polyphase.

4. 

p
V


 90
p
V
 Two Phase
System:
 A generator
consists of two
coils placed
perpendicular
to each other
 The voltage
generated by
one lags the
other by 90.

5.  Three Phase System:
 A generator consists of three coils placed 120 apart.
 The voltage generated are equal in magnitude but, out of
phase by 120.
 Three phase is the most economical polyphase system.

9.  Three things must be present in order to produce
electrical current:
a) Magnetic field
b) Conductor
c) Relative motion
 Conductor cuts lines of magnetic flux, a voltage is
induced in the conductor
 Direction and Speed are important

10. GENERATING A SINGLE PHASE
Motion is parallel to the flux.
No voltage is induced.
N
S

11. N
S
Motion is 45 to flux.
Induced voltage is 0.707 of maximum.
GENERATING A SINGLE PHASE

12. GENERATING A SINGLE PHASE
x
N
S
Motion is perpendicular to flux.
Induced voltage is maximum.

13. GENERATING A SINGLE PHASE
Motion is 45 to flux.
N
S
Induced voltage is 0.707 of maximum.

14. GENERATING A SINGLE PHASE
N
S
Motion is parallel to flux.
No voltage is induced.

15. GENERATING A SINGLE PHASE
N
S
Notice current in the
conductor has reversed.
Induced voltage is
0.707 of maximum.
Motion is 45 to flux.

16. GENERATING A SINGLE PHASE
N
S
Motion is perpendicular to flux.
Induced voltage is maximum.

17. GENERATING A SINGLE PHASE
N
S
Motion is 45 to flux.
Induced voltage is 0.707 of maximum.

18. GENERATING A SINGLE PHASE
Motion is parallel to flux.
N
S
No voltage is induced.
Ready to produce another cycle.

20.  The generator consists of a rotating magnet (rotor)
surrounded by a stationary winding (stator).
 Three separate windings or coils with terminals a-a’, b-
b’, and c-c’ are physically placed 120 apart around the
stator.
 As the rotor rotates, its magnetic field cuts the flux
from the three coils and induces voltages in the coils.
 The induced voltage have equal magnitude but out of
phase by 120.

21. GENERATION OF THREE-PHASE AC
N
x
x
S

22. THREE-PHASE WAVEFORM
Phase 2 lags phase 1 by 120. Phase 2 leads phase 3 by 120.
Phase 3 lags phase 1 by 240. Phase 1 leads phase 3 by 240.
Phase 1 Phase 2 Phase 3
120 120 120
240
120 120 120
240

23. Phase 1Phase 2 Phase 3
GENERATION OF 3 VOLTAGES
Phase 1 is ready to go positive.
Phase 2 is going more negative.
Phase 3 is going less positive.
N
x
x
S

25.  Balanced three phase voltages:
 same magnitude (VM )
 120 phase shift
 
 
   










120
cos
240
cos
)
(
120
cos
)
(
cos
)
(
t
V
t
V
t
v
t
V
t
v
t
V
t
v
M
M
cn
M
bn
M
an





26.  Balanced three phase currents:
 same magnitude (IM )
 120 phase shift
 
 
 










240
cos
)
(
120
cos
)
(
cos
)
(






t
I
t
i
t
I
t
i
t
I
t
i
M
c
M
b
M
a

27.  Balanced Phase Voltage: all phase voltages are equal in
magnitude and are out of phase with each other by
120.
 Balanced Load: the phase impedances are equal in
magnitude and in phase.

28. QUANTITY SYMBOL
Phase current I
Line current IL
Phase voltage V
Line voltage VL

29.  Phase voltage is measured between the neutral and any
line: line to neutral voltage
 Line voltage is measured between any two of the three
lines: line to line voltage.
 Line current (IL) is the current in each line of the source
or load.
 Phase current (I) is the current in each phase of the
source or load.

31. SOURCE LOAD CONNECTION
Wye Wye Y-Y
Wye Delta Y-
Delta Delta - 
Delta Wye -Y

32.  Common connection of source: WYE
 Delta connected sources: the circulating current may
result in the delta mesh if the three phase voltages are
slightly unbalanced.
 Common connection of load: DELTA
 Wye connected load: neutral line may not be
accessible, load can not be added or removed easily.

34. n
a
b
c
Vab
Vbc
Vca
Vbn
Vcn
Van
Ia
Ib
Ic

35. ZY
ZY
ZY
a
c
b
n
Load
ZY
Z
Y
Z
Y
a
b
c
Load
n
OR

37.  In Y-Y system:
φ
L I
I 

38.  Phase voltage is measured
between the neutral and any
line: line to neutral voltage
n
a
b
c
Vab
Vbc
Vca
Vbn
Vcn
Van
Ia
Ib
Ic
Van
Vbn
Vcn

39.  Line voltage is measured
between any two of the three
lines: line to line voltage.
n
a
b
c
Vab
Vbc
Vca
Vbn
Vcn
Van
Ia
Ib
Ic
Vab
Vbc
Vca
an
cn
ca
cn
bn
bc
bn
an
ab
V
V
V
V
V
V
V
V
V






VL=√3 VPh

40.  All phase voltages have the same magnitude,
 Out of phase with each other by 120
an bn cn
V V V V
   
= =

41.  All line voltages have the same magnitude,
 Out of phase with each other by 120
ab bc ca
V V V V
L   
= =

42. 



 30
V
VL 
1. Magnitude
2. Phase
- VL LEAD their corresponding V by 30
L
V 3 V


45. OR

47.  In - system, line voltages equal to phase voltages:
φ
L V
V 

48.  Phase voltages are equal to the voltages across the load
impedances.




49. Δ
CA
CA
Δ
BC
BC
Δ
AB
AB
Z
V
I
,
Z
V
I
,
Z
V
I 


 The phase currents are obtained:

50.  The line currents are obtained from the phase currents by
applying KCL at nodes A,B, and C.




51. BC
CA
c
AB
BC
b
CA
AB
a
I
I
I
I
I
I
I
I
I






IL=√3IPH

53.  All phase currents have the same magnitude,
 Out of phase with each other by 120
Δ
φ
CA
BC
AB
φ
Z
V
I
I
I
I 




54.  All line currents have the same magnitude,
 Out of phase with each other by 120
c
b
a
L I
I
I
I 



55. 1. Magnitude
Phase
- IL LAG their corresponding I by 30

I
IL 3





 30
I
IL 