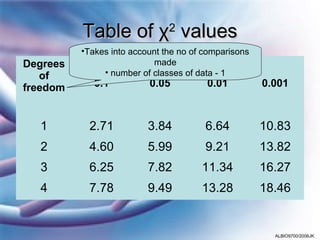
The chi-squared (χ2) test allows researchers to compare observed results to expected results and determine if any differences are statistically significant. The χ2 value is calculated by summing the squared differences between observed and expected values, divided by the expected value. Higher χ2 values indicate a lower probability that the differences are due to chance, as determined by comparing the χ2 value to a table of critical values. An example problem demonstrates using a χ2 test to analyze the results of a genetic cross.

1. The χ 2 (chi-squared) Test
χ 2 = ∑ (O – E) 2
E
where ∑ = the sum of
O = the observed value
E = the expected value
ALBIO9700/2006JK

2. Questions:
• Are the results we get (observed)
sufficiently close to the ones we expected
that the differences between them have
probably just arisen by chance?
• Are they so different that something
unexpected must be going on?
ALBIO9700/2006JK

3. Answers:
• The χ2 (chi-squared) test allows us to
compare our observed results with the
expected results
• Decide whether or not there is a significant
difference between them
ALBIO9700/2006JK

4. Calculations:
1. Work out expected results
2. Record in table with observed results
3. Calculate difference between each set
and square it
4. Divide each squared difference by the
expected value and add up
ALBIO9700/2006JK

5. What the value means?
• Relate χ2 (chi-squared) value to probabilities in
“Table of χ2 values”
• The probabilities are the probability that the
difference between our expected and observed
results are due to chance
ALBIO9700/2006JK

6. Table of χ values 2
•Takes into account the no of comparisons
Degrees made
Probability greater than
of • number of classes of data - 1
freedom 0.1 0.05 0.01 0.001
1 2.71 3.84 6.64 10.83
2 4.60 5.99 9.21 13.82
3 6.25 7.82 11.34 16.27
4 7.78 9.49 13.28 18.46
ALBIO9700/2006JK

7. Problem:
In an actual cross between heterozygous grey
parents with a long tail, the number of each
phenotype obtained in the offspring were:
grey, long 54
grey, short 4
white, long 4
white, short 18
Use a χ2 test to determine whether or not the
difference between these observed results and
the expected results is significant.
ALBIO9700/2006JK