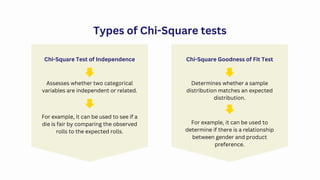
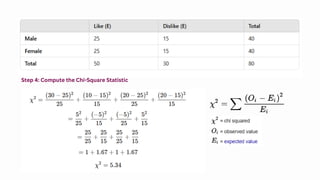
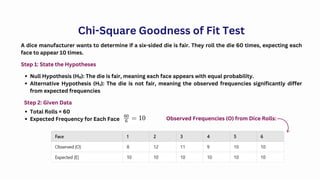
The Chi-Square test is a powerful statistical tool used to analyze categorical data by comparing observed and expected frequencies. It helps determine whether a dataset follows an expected distribution (Goodness-of-Fit Test) or whether two categorical variables are related (Test for Independence). Being a non-parametric test, it is widely applicable but requires large sample sizes and independent observations for reliable results. While it identifies associations between variables, it does not measure causation or the strength of relationships. Despite its limitations, the Chi-Square test remains a fundamental method in statistics for hypothesis testing in various fields.