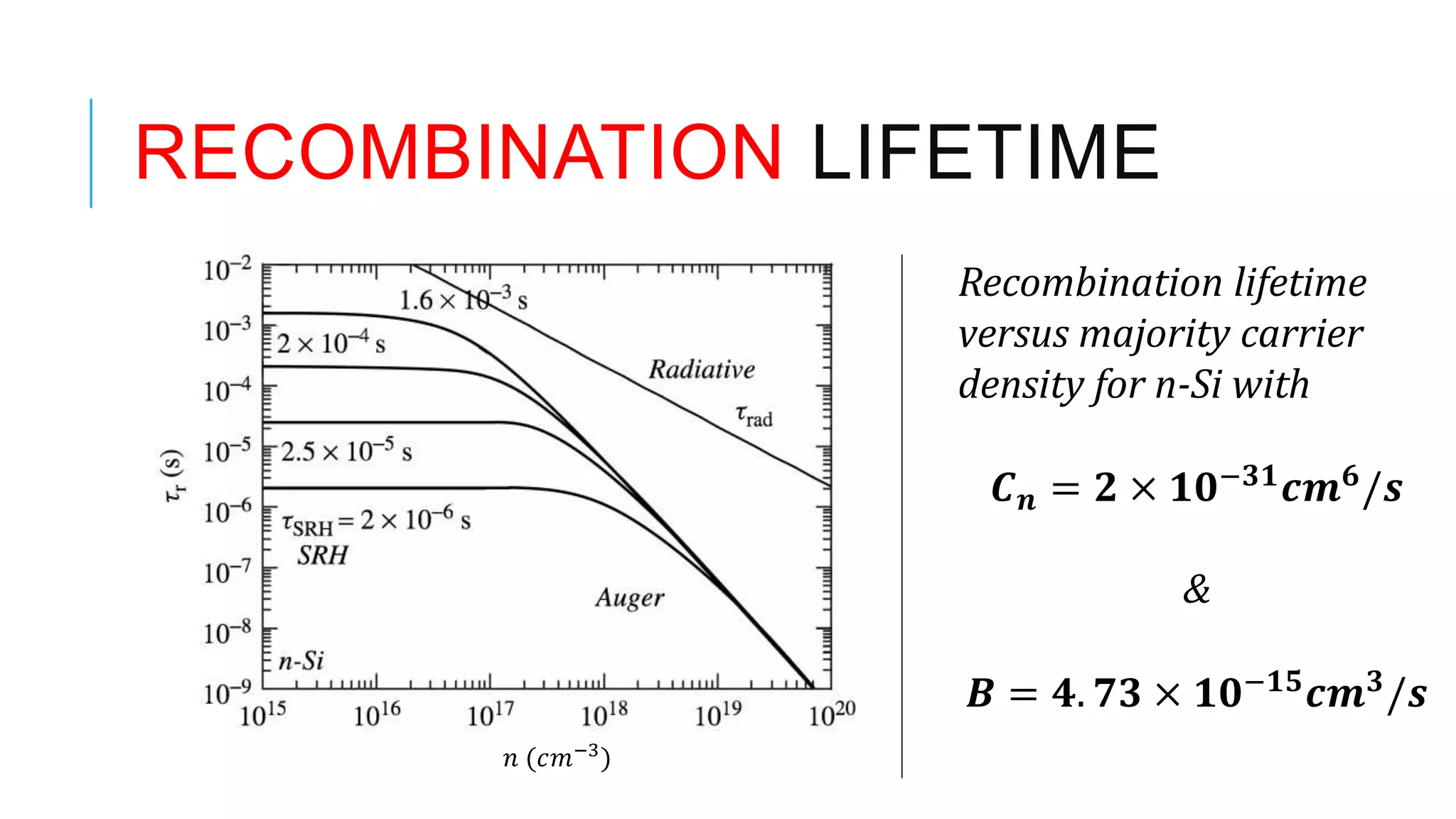
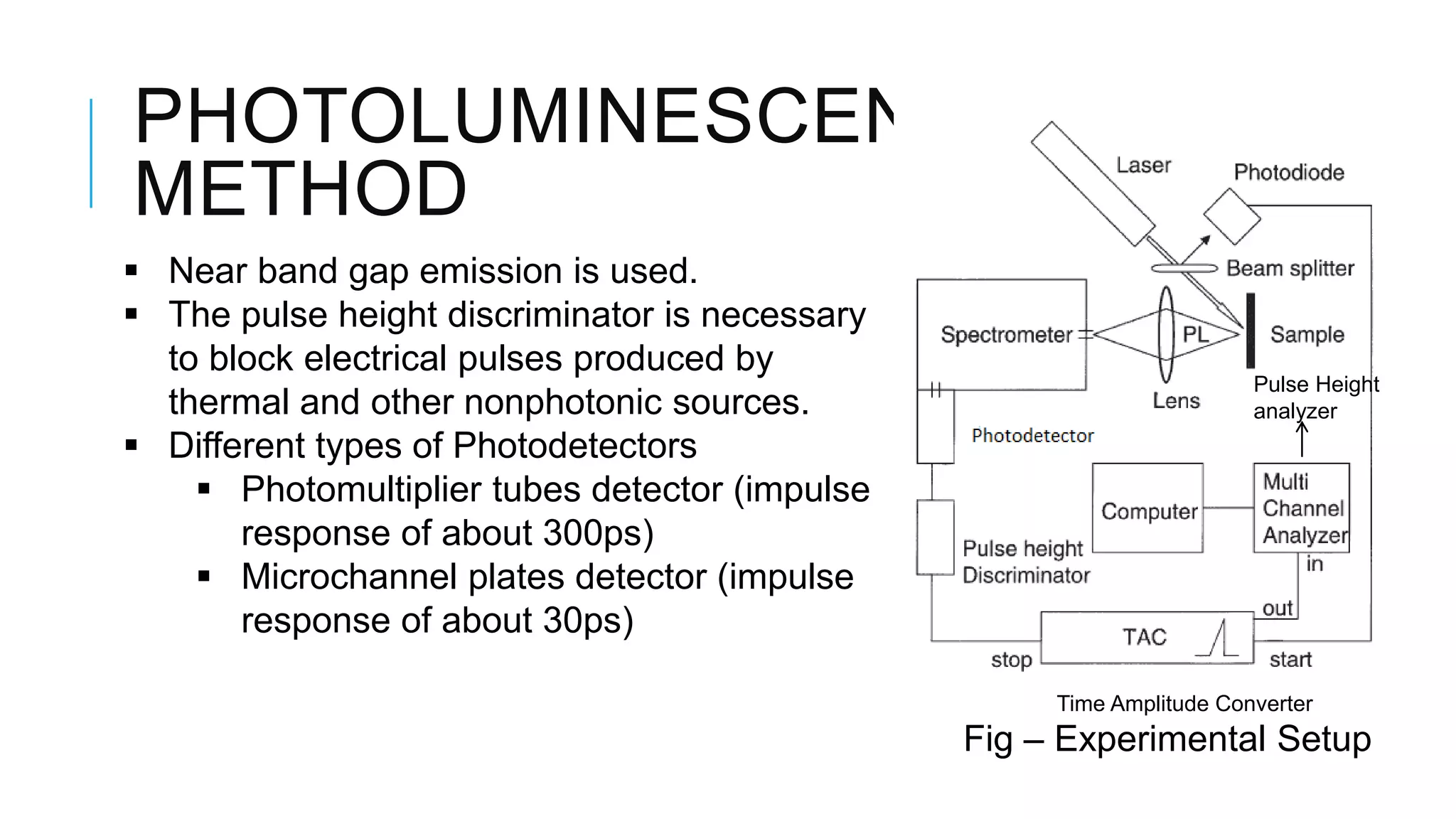
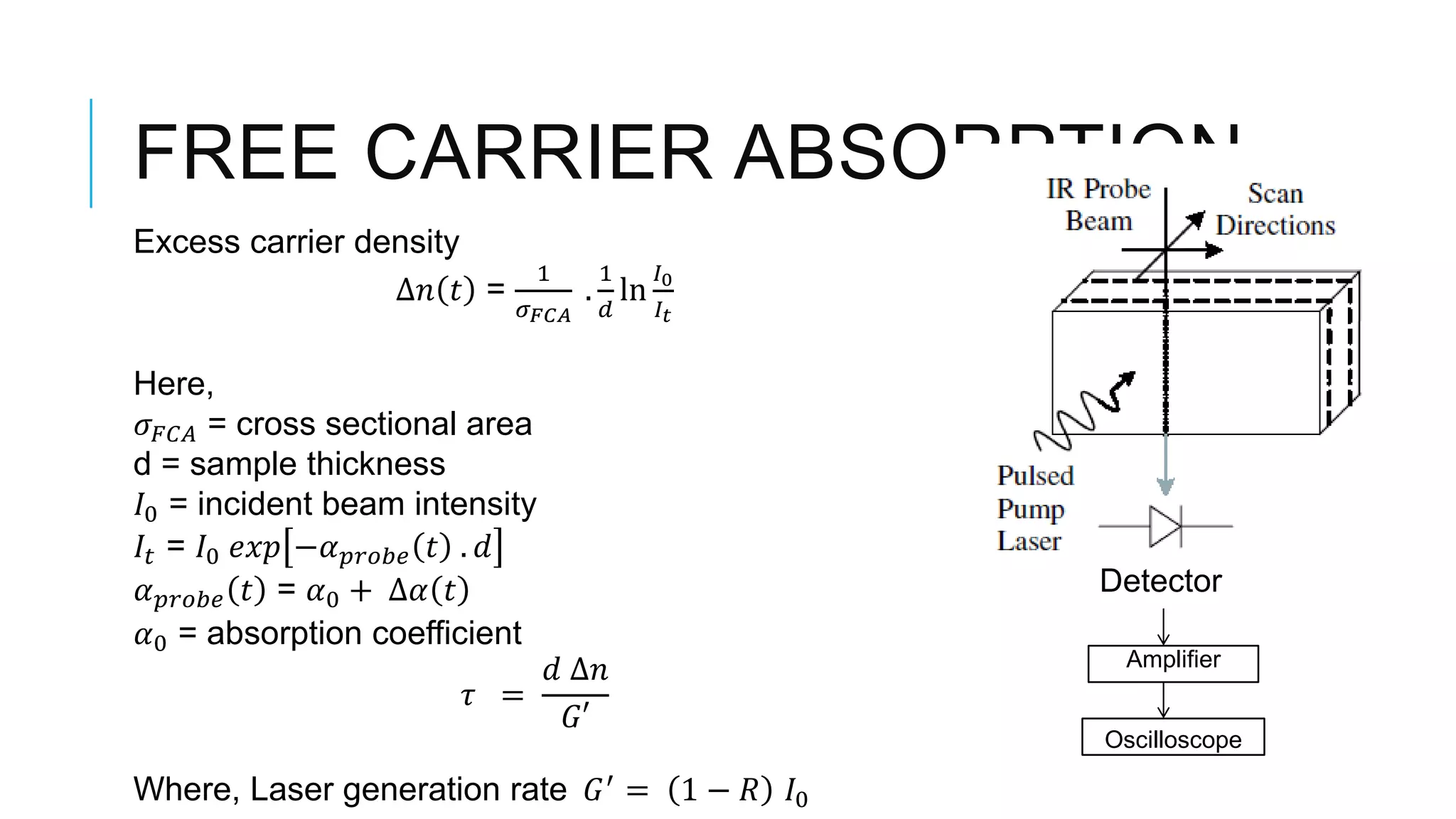
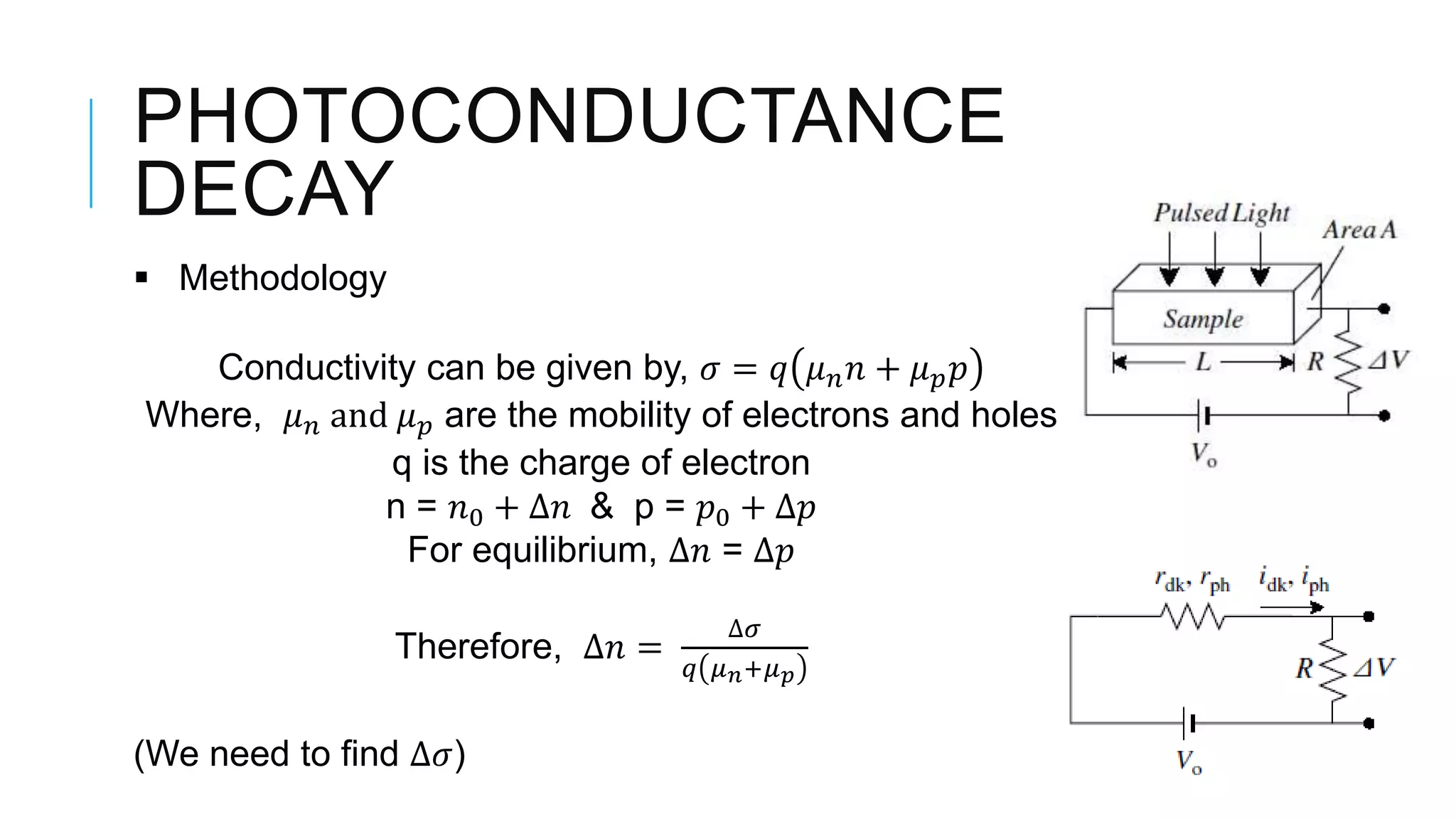
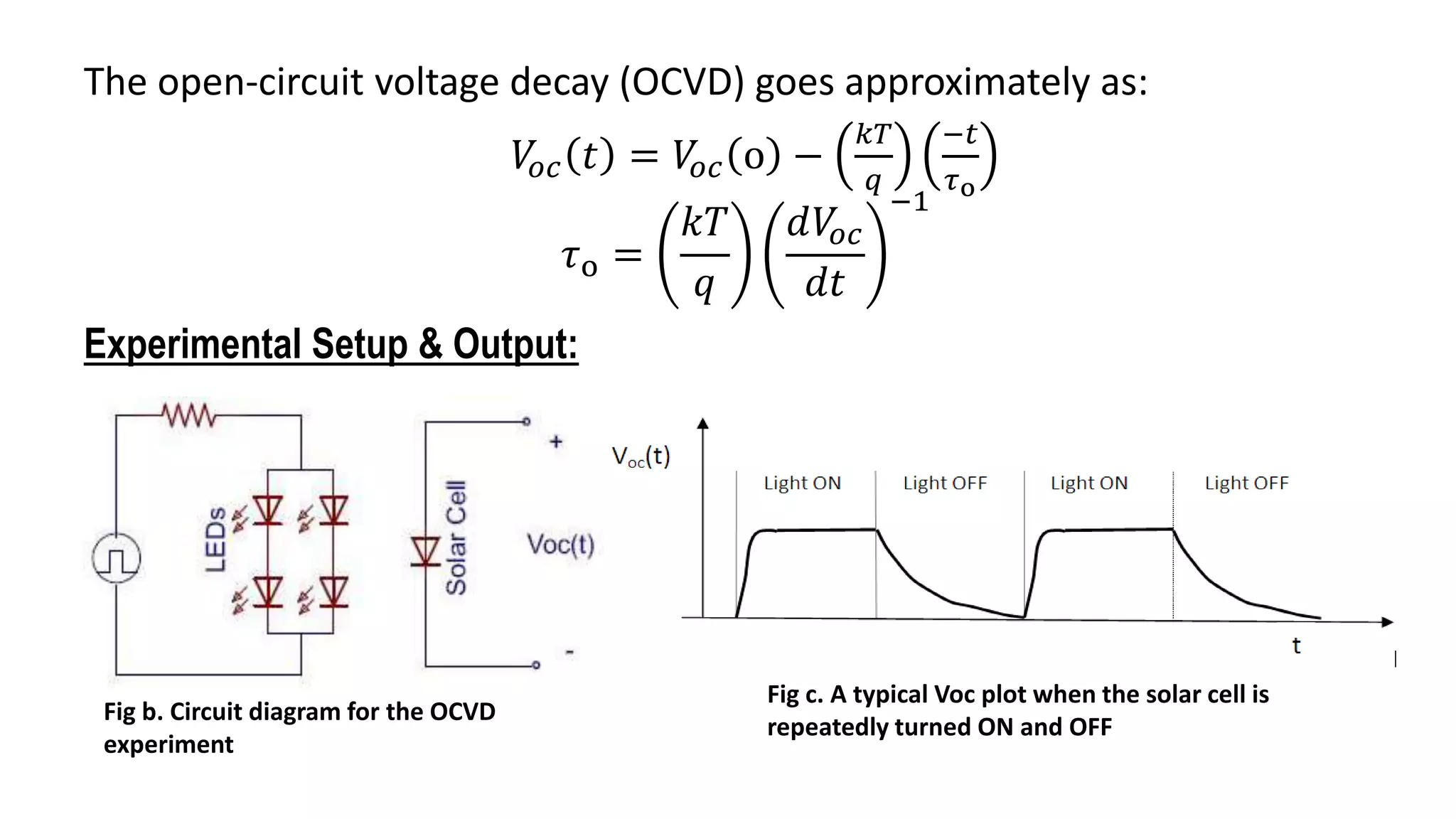
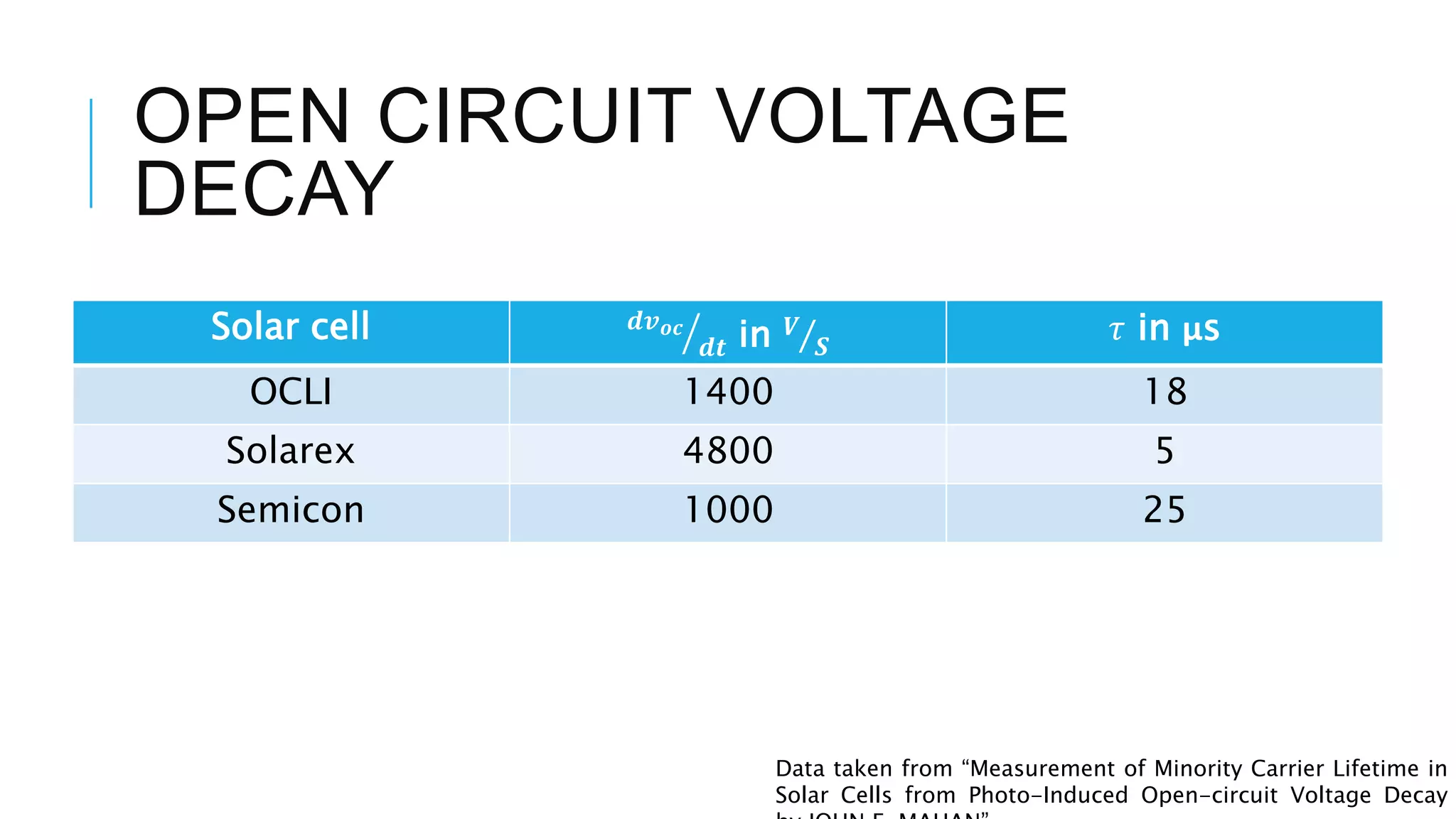
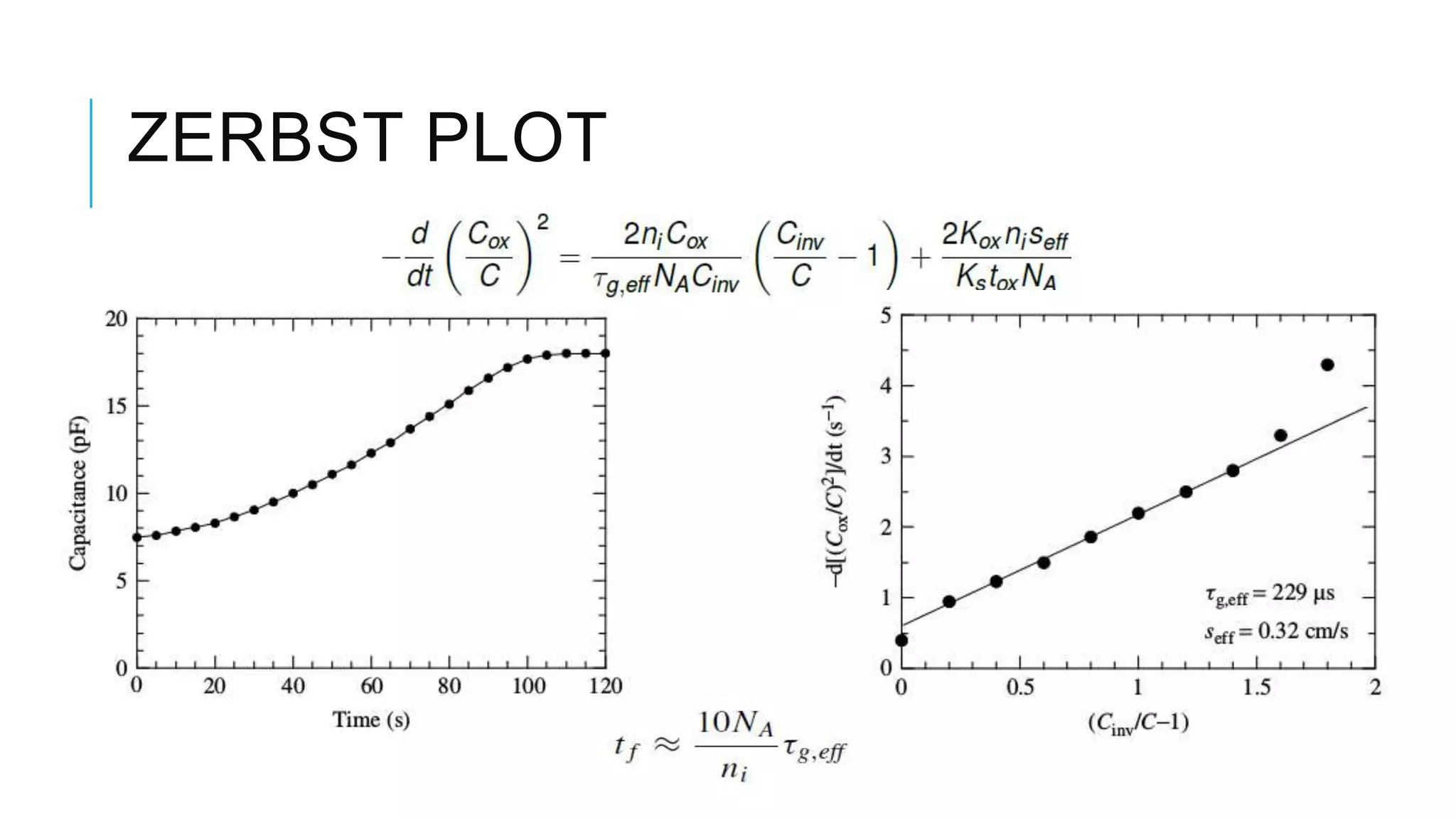
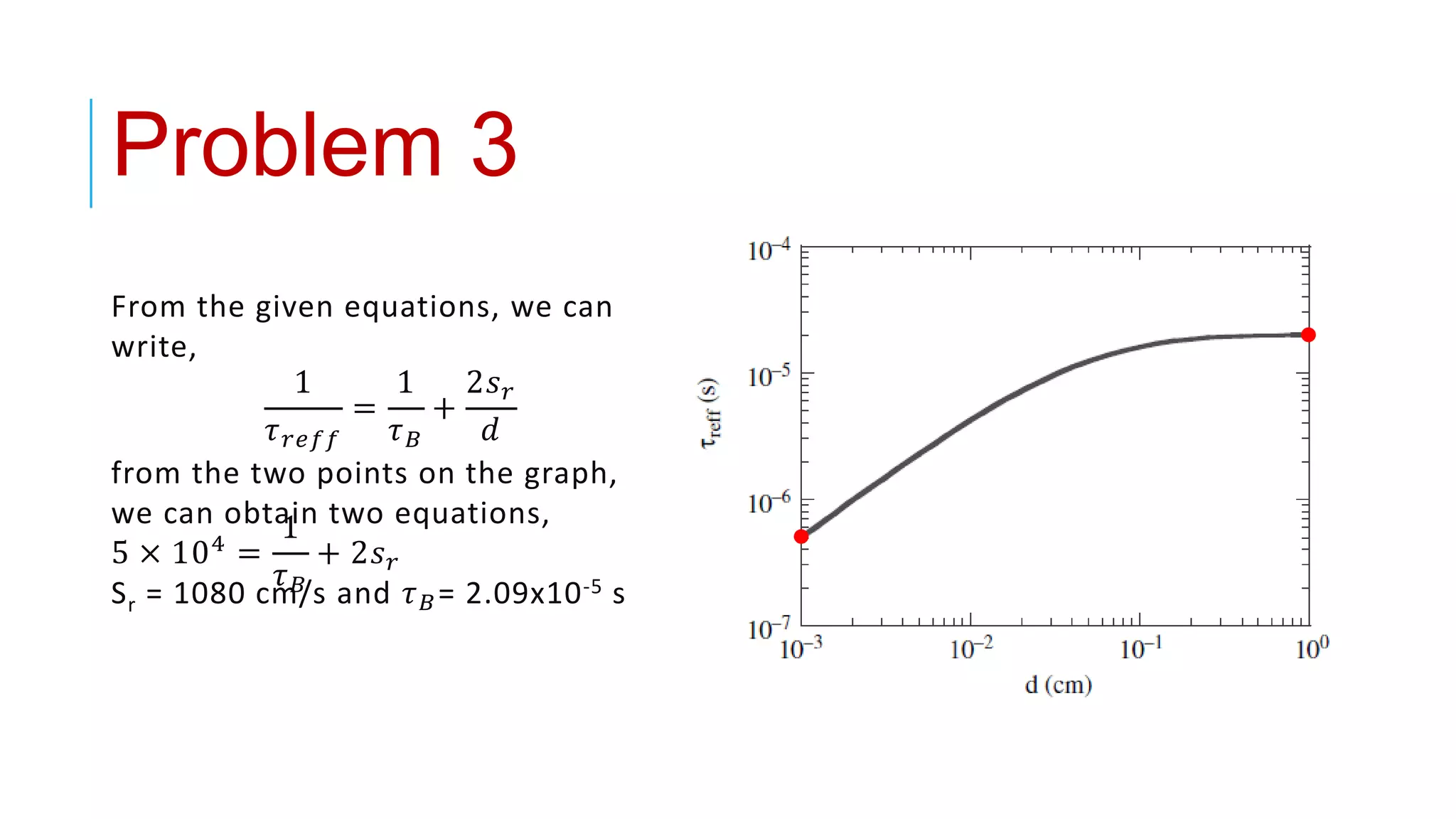
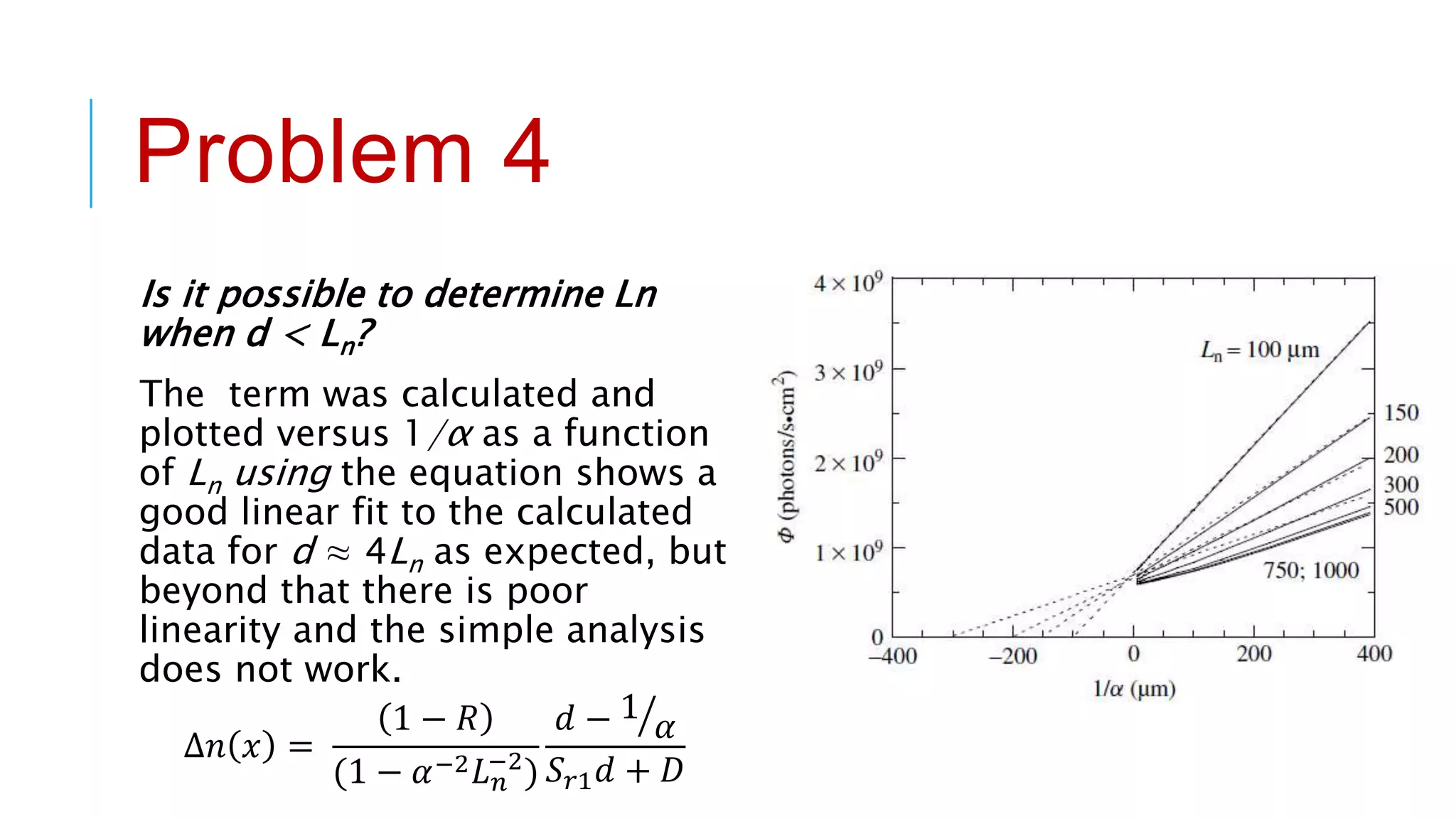
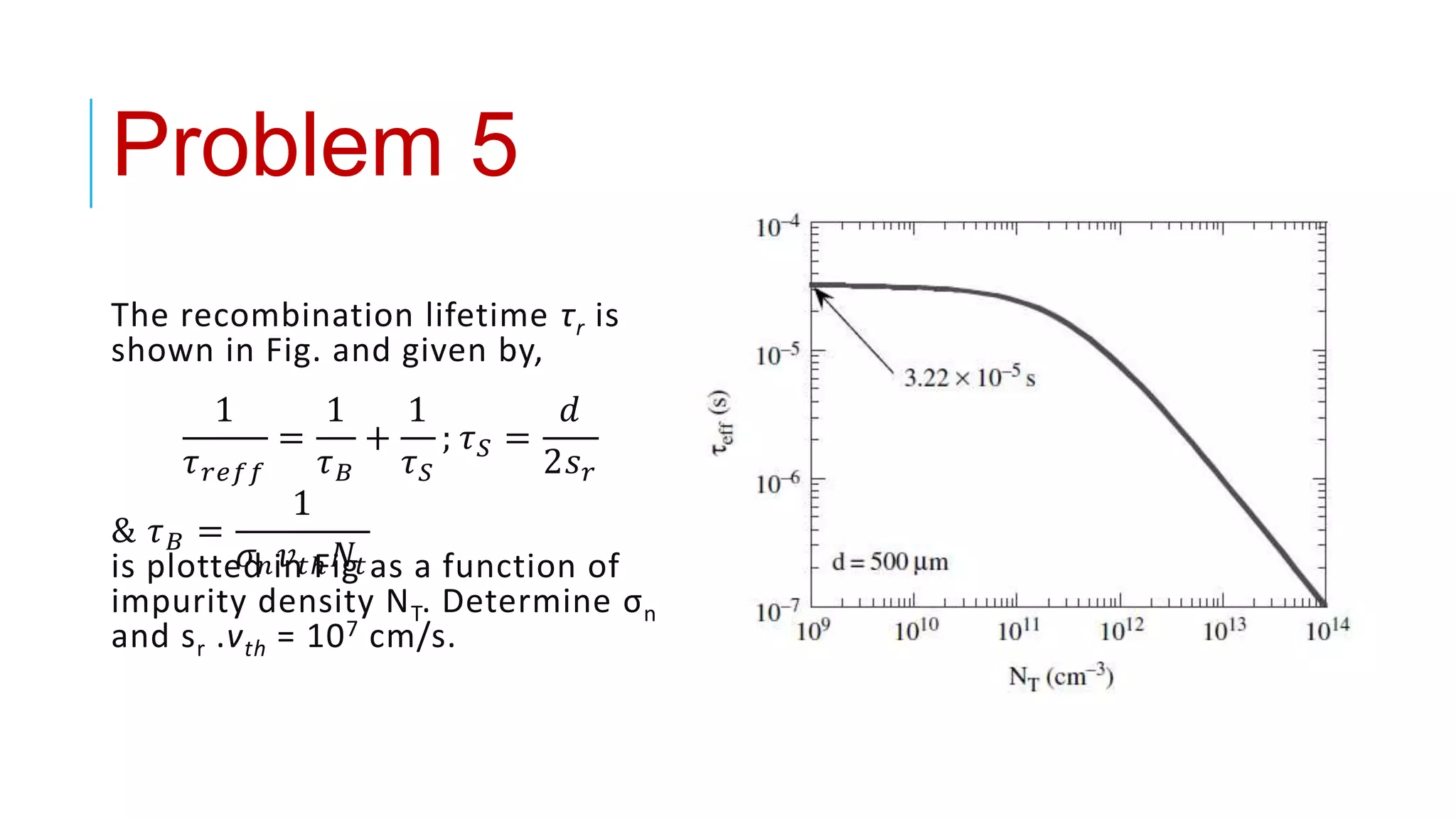
This document provides an overview of carrier lifetime characterization techniques. It discusses that carrier lifetime determines the performance of semiconductor devices and solar cells. It then defines recombination lifetime and generation lifetime. The document proceeds to describe various optical methods to measure carrier lifetime, including photoluminescence, free carrier absorption, photoconductance decay, and their advantages and disadvantages. It provides equations to calculate carrier lifetime from measurements of excess carrier density, conductivity change, and voltage change.

1. Characterization of Carrier
Lifetime
Presentation as part of internal assessment in course
Semiconductor Processing & Characterization
M.Tech Solar, PDPU.
Presented to
Prof. Manoj Kumar
Presented by
Aditya Soni
(17MSE001)
Jay Joshi
(17MSE005)
Mrunmayee Unawane
(17MSE016)

2. CARRIER LIFETIMES – WHY
MEASURE THEM
In IC Industries,
• Carrier lifetime determines
performance of devices.
• It is a sensitive measure of
material quality and
cleanliness.
• It gives information about
defect densities as low as
to 1o11 cm-3
8/18/2018
In Solar Cells,
•Carrier lifetime of minority
carriers determines
performance of the solar cell.
•Longer the minority carries
retain the energy
corresponding to the
conduction band, higher their
probability to cross the SCR
and contribute in conduction.
Band diagram of Solar
Cell under illumination.

3. ℎ𝜈
CARRIER LIFETIMES – WHAT
ARE THEY
Recombination lifetime
𝜏 𝑟:
Excess carriers decay by
recombining
 𝜏 𝑟 is the average time after
which the electron goes
back in the valence band
and recombines with it’s
hole.
8/18/2018
E
v
Ec
𝑛𝑜𝑛 𝑟𝑎𝑑𝑖𝑎𝑡𝑖𝑣𝑒 𝑒𝑚𝑚𝑖𝑠𝑖𝑜𝑛
𝑛𝑜𝑛 𝑟𝑎𝑑𝑖𝑎𝑡𝑖𝑣𝑒 𝑒𝑚𝑚𝑖𝑠𝑖𝑜𝑛
𝑅−𝐺 𝐶𝑒𝑛𝑡𝑒𝑟𝑠
E
v
Ec
• Band to Band recombination
• SRH Recombination
• Auger recombination
E
v
Ec

4. CARRIER LIFETIMES – WHAT
ARE THEY
Generation lifetime 𝜏 𝑔:
In case of lack of carriers,
electron-hole pairs are
generated.
 𝜏 𝑔 is the average time
which the electron hole
is generated.
 Misnomer - Generation
Time.
8/18/2018
• Thermal Generation
• Optical Generation
• Impact Ionization
generation
E
v
Ec
Ef
T = o K T > o K
E
v
Ec
ℎ𝜈 > 𝐸 𝑔
An carrier with enough
kinetic energy can knock
a bound electron out of
its bound state and
promote it to a state in
the conduction band,
creating an electron-hole
pair.

5. RECOMBINATION LIFETIME
8/18/2018
𝜏 𝑆𝑅𝐻 =
𝜏 𝑝 𝑛 𝑜 + 𝑛 + ∆𝑛 + 𝜏 𝑛(𝑝o+𝑝 + ∆𝑝)
𝑝o +𝑛o +∆𝑛
𝜏 𝑅𝑎𝑑 =
1
𝐵(𝑝o +𝑛o +∆𝑛)
𝜏 𝐴𝑢𝑔𝑒𝑟 =
1
𝐶 𝑝(𝑝o
2
+2𝑝o∆𝑛 + ∆𝑛2) + 𝐶 𝑛(𝑛o
2
+ 2𝑛o∆𝑛 + ∆𝑛2)
𝑁 𝑇= 𝐷𝑒𝑛𝑠𝑖𝑡𝑦
𝑣𝑡ℎ= 𝑇ℎ𝑒𝑟𝑚𝑎𝑙 𝑉𝑒𝑙𝑜𝑐𝑖𝑡𝑦
𝜎 𝑝 = 𝑐𝑎𝑝𝑡𝑢𝑟𝑒 𝑐𝑟𝑜𝑠𝑠-𝑠𝑒𝑐𝑡𝑖𝑜𝑛𝑠 𝑜𝑓 ℎ𝑜𝑙𝑒𝑠
𝜎n = 𝑐𝑎𝑝𝑡𝑢𝑟𝑒 𝑐𝑟𝑜𝑠𝑠-𝑠𝑒𝑐𝑡𝑖𝑜𝑛𝑠 𝑜𝑓 electrons
𝑛 = 𝑒𝑙𝑒𝑐𝑡𝑟𝑜𝑛 𝑐𝑜𝑛𝑐𝑒𝑛𝑡𝑟𝑎𝑡𝑖𝑜𝑛
𝑝 = ℎ𝑜𝑙𝑒 𝑐𝑜𝑛𝑐𝑒𝑛𝑡𝑟𝑎𝑡𝑖𝑜𝑛
𝑛o = 𝑒𝑞𝑢𝑖𝑙𝑙𝑖𝑏𝑟𝑖𝑢𝑚 𝑒− 𝑐𝑜𝑛𝑐𝑒𝑛𝑡𝑟𝑎𝑡𝑖𝑜𝑛
𝑝o = 𝑒𝑞𝑢𝑖𝑙𝑙𝑖𝑏𝑟𝑖𝑢𝑚 ℎ+ 𝑐𝑜𝑛𝑐𝑒𝑛𝑡𝑟𝑎𝑡𝑖𝑜𝑛
Δ𝑛= 𝑒𝑥𝑐𝑒𝑠𝑠 𝑒− 𝑐𝑜𝑛𝑐𝑒𝑛𝑡𝑟𝑎𝑡𝑖𝑜𝑛
𝛥𝑝= 𝑒𝑥𝑐𝑒𝑠𝑠 ℎ+ 𝑐𝑜𝑛𝑐𝑒𝑛𝑡𝑟𝑎𝑡𝑖𝑜𝑛
𝜏 𝑝 =
1
𝜎 𝑝 𝑣 𝑡ℎ 𝑁𝑡
𝜏 𝑛 =
1
𝜎 𝑛 𝑣 𝑡ℎ 𝑁𝑡
𝟏
𝝉 𝒓
=
𝟏
𝝉 𝑹𝒂𝒅
+
𝟏
𝝉 𝑺𝑹𝑯
+
𝟏
𝝉 𝑨𝒖𝒈𝒆𝒓

6. RECOMBINATION LIFETIME
8/18/2018
𝜏 𝐴𝑢𝑔𝑒𝑟 =
1
𝐶 𝑝(𝑝o
2
+2𝑝o∆𝑛 + ∆𝑛2) + 𝐶 𝑛(𝑛o
2
+ 2𝑛o∆𝑛 + ∆𝑛2)
𝜏 𝑅𝑎𝑑 =
1
𝐵(𝑝o +𝑛o +∆𝑛)

7. RECOMBINATION LIFETIME
𝑛 (𝑐𝑚−3)
Recombination lifetime
versus majority carrier
density for n-Si with
𝑪 𝒏 = 𝟐 × 𝟏𝟎−𝟑𝟏 𝒄𝒎 𝟔/𝒔
&
𝑩 = 𝟒. 𝟕𝟑 × 𝟏𝟎−𝟏𝟓 𝒄𝒎 𝟑/𝒔

8. GENERATION LIFETIME
8/18/2018
𝜏 𝑔 = 𝜏 𝑝 𝑒𝑥𝑝
𝐸 𝑇 − 𝐸𝑖
𝑘𝑇
+ 𝜏 𝑛 𝑒𝑥𝑝 −
𝐸 𝑇 − 𝐸𝑖
𝑘𝑇
E 𝑇 = Energy Level
Ei = Intrinsic Energy Level
𝜏 𝑝 =
1
𝜎 𝑝 𝑣 𝑡ℎ 𝑁𝑡
𝜏 𝑛 =
1
𝜎 𝑛 𝑣 𝑡ℎ 𝑁𝑡

9. OPTICAL METHODS
Different methods available
 Photoluminescence method (PL)
 Free carrier absorption (FCA)
 Photoconductance Decay (PCD)
 Short circuit current / open circuit voltage decay (SCCD /
 Surface Voltage
 Steady state short circuit current method (SSSCC)
 Electron beam induced current (EBIC)
 Quasi steady state photoconductance (QSSP)

10. PHOTOLUMINESCENCE
METHOD
 Near band gap emission is used.
 The pulse height discriminator is necessary
to block electrical pulses produced by
thermal and other nonphotonic sources.
 Different types of Photodetectors
 Photomultiplier tubes detector (impulse
response of about 300ps)
 Microchannel plates detector (impulse
response of about 30ps)
Fig – Experimental Setup
Time Amplitude Converter
Pulse Height
analyzer

11. PHOTOLUMINESCENCE
METHOD
• Advantages
• Non contact method
• Also can be used for
determining the composition of
compound Semiconductors,
such as 𝐴𝑙 𝑥 𝐺𝑎1−𝑥 𝐴𝑠 by using
shallow emission or deep level
emissions
Fig – Experimental Setup
Time Amplitude Converter
Pulse Height
analyzer

12. PHOTOLUMINESCENCE
METHOD
• Disadvantages
• Costly equipment required
• Not so accurate for the
characterization of indirect band
gap semiconductors
• Not a bulk characterization
technique
• Only a thin, near surface region
can be investigated.
• Error can occur if the photon
recycling happens
Fig – Experimental Setup
Time Amplitude Converter
Pulse Height
analyzer

13. PHOTON RECYCLING
 Basically, it is the recapturing of photon
 It may give you the carrier lifetime well above the theoretical value
 It could be corrected by adding the photon recycling factor in the final
equation
ℎ𝜈
E
v
Ec

14. FREE CARRIER ABSORPTION
Excess carrier density
∆𝑛 𝑡 =
1
𝜎 𝐹𝐶𝐴
.
1
𝑑
ln
𝐼0
𝐼𝑡
Here,
𝜎 𝐹𝐶𝐴 = cross sectional area
d = sample thickness
𝐼0 = incident beam intensity
𝐼𝑡 = 𝐼0 𝑒𝑥𝑝 −𝛼 𝑝𝑟𝑜𝑏𝑒 𝑡 . 𝑑
𝛼 𝑝𝑟𝑜𝑏𝑒 𝑡 = 𝛼0 + ∆𝛼 𝑡
𝛼0 = absorption coefficient
𝜏 =
𝑑 ∆𝑛
𝐺′
Where, Laser generation rate 𝐺′
= 1 − 𝑅 𝐼0
Detector
Amplifier
Oscilloscope

15. FREE CARRIER ABSORPTION
Detector
 Pump Laser Selection
 From experiments, it is observed that a
yttrium-aluminum-garnet (YAG) laser
operating at λ = 1.06 μm is ideally
suited for Si wafers (around 350 μm
thick) because of its low absorption
coefficient.
 Pulse duration must be kept below the
shortest expected lifetime in the
sample, minimum beam size should be
at least a few carrier diffusion lengths in
diameter.
Amplifier
Oscilloscope

16. FREE CARRIER ABSORPTION
 Probe Laser Selection
 long wavelengths toward the IR range
are preferable and the choice is often set
by laser availability.
 As probe lasers, HeNe lasers are
traditionally used at operating
wavelengths of 3.39, 1.3, or 0.632 μm,
depending on band gap.
 Also, relatively intense lasers (high
temperature) have become available
offering increased measurement speed,
although care must be taken not to affect
the carrier dynamics by heating.
Detector
Amplifier
Oscilloscope

17. FREE CARRIER ABSORPTION
 Detection Electronics
 Reduction of noise is the priority
here.
 To reduce noise, oscilloscopes with
minimum bandwidth is selected.
 Digital oscilloscope is preferred over
the analog because of the provision
of digital averaging.
Detector
Amplifier
Oscilloscope

18. FREE CARRIER ABSORPTION
 Advantages
 Non contact method
 Suitable for bulk lifetime measurements
 Able to measure through very different sample
structures and semiconductor materials
 Disadvantages
 Surface recombination decreases the
accuracy
 Thus, it is accurate in short carrier lifetimes
(for example, indirect-band-gap
semiconductors.
 At low carrier concentration, the optical
Detector
Amplifier
Oscilloscope

19. PHOTOCONDUCTANCE
DECAY
 Methodology
𝜕∆𝑛(𝑡)
𝜕𝑡
= G – R = G -
∆𝑛(𝑡)
𝜏 𝑒𝑓𝑓
(Continuity equation)
For PCD, G(t) <<
𝜕∆𝑛(𝑡)
𝜕𝑡
Therefore, 𝜏 𝑒𝑓𝑓(∆𝑛) = -
∆𝑛(𝑡)
𝜕∆𝑛(𝑡)
𝜕𝑡
(We need to find ∆𝑛)

20. PHOTOCONDUCTANCE
DECAY
 Methodology
Conductivity can be given by, 𝜎 = 𝑞 𝜇 𝑛 𝑛 + 𝜇 𝑝 𝑝
Where, 𝜇 𝑛 and 𝜇 𝑝 are the mobility of electrons and holes
q is the charge of electron
n = 𝑛0 + ∆𝑛 & p = 𝑝0 + ∆𝑝
For equilibrium, ∆𝑛 = ∆𝑝
Therefore, ∆𝑛 =
∆𝜎
𝑞 𝜇 𝑛+𝜇 𝑝
(We need to find ∆𝜎)

21. PHOTOCONDUCTANCE
DECAY
∆𝑉 = 𝑖 𝑝ℎ − 𝑖 𝑑𝑘 𝑅
Here, ∆𝑉 is the voltage change between the dark and the
illuminated sample.
𝑖 𝑝ℎ & 𝑖 𝑑𝑘 are photocurrent and dark current.
Conductivity ∆𝑔 = 𝑔 𝑝ℎ − 𝑔 𝑑𝑘 =
1
𝑟 𝑝ℎ
−
1
𝑟 𝑑𝑘
∆𝑔 = ∆𝜎𝐴
𝐿
(We need to find ∆𝑔 )

22. PHOTOCONDUCTANCE
DECAY
∆𝑉 =
𝑅 ∆𝑔 𝑣0 𝑟𝑑𝑘
2
𝑅 + 𝑟𝑑𝑘 (𝑅 + 𝑟𝑑𝑘 + 𝑅𝑟𝑑𝑘∆𝑔)
For constant voltage, the above equation can be written
as
∆𝑉 = 𝑅 ∆𝑔 𝑣0 1 −
∆𝑉
𝑉0
Form this equation, we get ∆𝑔.

23. VERDICT
Versatile techniques. Can be used for several different
conductors.
Non contact method, which means simple or no sample
preparation.
You may get an error in the calculation if carrier trapping
is dominant.
They require comparatively complex experimental setup.

24. ELECTRICAL MEASUREMENT
TECHNIQUES
Diode-based:
• Open-circuit voltage decay (𝜏 𝑟)
• Reverse-recovery (𝜏 𝑟)
Pulsed MOS capacitor method (𝜏 𝑟):
• Inversion method
8/18/2018

25. ELECTRICAL MEASUREMENT
TECHNIQUES
Pulsed MOS capacitor method (τg):
•Deep depletion method and Zerbst plot
•Current-capacitance
8/18/2018

26. OPEN-CIRCUIT VOLTAGE
DECAY (OCVD)
Fig a. Plot of the decay of Voc with time
The carriers decay
exponentially, due to
recombination given by
𝑛 = 𝐴𝑒𝑥𝑝(
−𝑡
𝜏o
)
The open‐circuit voltage
decay (OCVD) goes
approximately as:
𝑉𝑜𝑐 𝑡 = 𝑉𝑜𝑐 o −
𝑘𝑇
𝑞
−𝑡
𝜏o
𝑉𝑜𝑐(𝑡)
𝑉𝑜𝑐(o)

27. The open‐circuit voltage decay (OCVD) goes approximately as:
𝑉𝑜𝑐 𝑡 = 𝑉𝑜𝑐 o −
𝑘𝑇
𝑞
−𝑡
𝜏o
𝜏o =
𝑘𝑇
𝑞
𝑑𝑉𝑜𝑐
𝑑𝑡
−1
Experimental Setup & Output:
Fig b. Circuit diagram for the OCVD
experiment
Fig c. A typical Voc plot when the solar cell is
repeatedly turned ON and OFF

28. OPEN CIRCUIT VOLTAGE
DECAY
Solar cell 𝒅𝒗 𝒐𝒄
𝒅𝒕 in 𝑽
𝑺
𝜏 in μs
OCLI 1400 18
Solarex 4800 5
Semicon 1000 25
Data taken from “Measurement of Minority Carrier Lifetime in
Solar Cells from Photo-Induced Open-circuit Voltage Decay

29. REVERSE RECOVERY (RR)
Fig a. Circuit
Schematic
Fig b. Plot of reverse recovery of a solar cell under
transient condition
V(t)
V(f)
V t
t
i(t) I(f)
-Ir ts𝑡 𝑠 = 𝜏 𝑜ln 1 +
𝐼𝑓
𝐼𝑟

30. CONCEPT OF MOS
CAPACITOR
Fig a: Structure of MOS Capacitor
𝐶 =
𝐶 𝑜𝑥 × 𝐶 𝑑
𝐶 𝑜𝑥 + 𝐶 𝑑
Total Capacitance C is given by,

31. CARRIER DISTRIBUTION IN
MOS STRUCTURE
Accumulation Depletion
Inversion

32. C-V CHARACTERISTICS OF A
MOS STRUCTURE
Characteristic of structure at
a- Low Frequency
b- High Frequency
c- High Frequency with pulsed bias
Methods are based on return of pulsed
MOS to equilibrium from
Accumulation towards depletion
Inversion towards depletion

33. DEEP DEPLETION METHOD
The MOS receives voltage pulses, going from equilibrium to deep
depletion: the capacitance is observed as the MOS comes back to
equilibrium via thermal generation of carriers.
Fig a. The C–VG and C − t behavior of an MOS-C pulsed into
deep depletion.

34. ZERBST PLOT

35. CURRENT-CAPACITANCE
Advantages:
Does not require differentiation of
experimental data
Doping concentration need not be
known
Measurement time required is less
Fig a. Current Vs Inverse
Capacitance Plot

36. CONCLUSIONS
Electrical Measurements methods are technically
simple as they are based on current, voltage and
capacitance methods.
Recombination lifetimes are best measured by optical
methods, while generation lifetimes prefer the MOS
capacitor method, especially for thin layers like
epitaxial layers.

37. The recombination lifetime τr is
shown in Fig. and given by,
1
𝜏 𝑟
=
1
𝜏 𝑅𝑎𝑑
+
1
𝜏 𝑆𝑅𝐻
+
1
𝜏 𝐴𝑢𝑔𝑒𝑟
Determine σpNT and C for device
(i) and σpNT and B for device (ii).
vth = 107 cm/s.
Problem

38. Problem 1
For device (i),
𝜏 𝑆𝑅𝐻 =
1
𝜎 𝑝 𝑣 𝑡ℎ 𝑁𝑡
= 5 × 10−6
𝑠𝑒𝑐
𝜎 𝑝 𝑣 𝑡ℎ 𝑁𝑡 =
1
5 × 10−6
𝜎 𝑝 𝑁𝑡 =
1
5 × 10−6 × 107
𝜎 𝑝 𝑁𝑡 = 0.02
Also from 2 points we get the equations,
𝐵 × 1019
+ 𝐶 × 1038
= 998 × 105
𝑎𝑛𝑑 𝐵 × 1019 + 40𝐶 × 1036 = 245 × 105
Solving these we get 𝐶 = 125.5 ×
10−32
𝑐𝑚6
/𝑠

39. Problem 2
For device (ii),
𝜏 𝑆𝑅𝐻 =
1
𝜎 𝑝 𝑣 𝑡ℎ 𝑁𝑡
= 5 × 10−7
𝑠𝑒𝑐
𝜎 𝑝 𝑣 𝑡ℎ 𝑁𝑡 =
1
5 × 10−7
𝜎 𝑝 𝑁𝑡 =
1
5 × 10−7 × 107
𝜎 𝑝 𝑁𝑡 = 0.2
Also from 2 points we get the equations,
5𝐵 × 1018
+ 25𝐶 × 1036
= 488 × 106
𝑎𝑛𝑑 25𝐵 × 1019
+ 25𝐶 × 1036
= 244 × 108
Solving these we get 𝐵 = 97.6 × 10−12 𝑐𝑚6/
𝑠

40. The effective recombination
lifetime is shown in fig. As a
function of wafer thickness; all
samples have identical τB and sr.
1
𝜏 𝑟𝑒𝑓𝑓
=
1
𝜏 𝐵
+
1
𝜏 𝑆
; 𝜏 𝑆 =
𝑑
2𝑠 𝑟
Determine τB and sr .
Problem 3

41. From the given equations, we can
write,
1
𝜏 𝑟𝑒𝑓𝑓
=
1
𝜏 𝐵
+
2𝑠 𝑟
𝑑
from the two points on the graph,
we can obtain two equations,
5 × 104 =
1
𝜏 𝐵
+ 2𝑠 𝑟
Sr = 1080 cm/s and 𝜏 𝐵= 2.09x10-5 s
Problem 3

42. Problem 4
Is it possible to determine Ln
when d < Ln?
The term was calculated and
plotted versus 1/α as a function
of Ln using the equation shows a
good linear fit to the calculated
data for d ≈ 4Ln as expected, but
beyond that there is poor
linearity and the simple analysis
does not work.
∆𝑛 𝑥 =
1 − 𝑅
(1 − 𝛼−2 𝐿 𝑛
−2
)
𝑑 − 1
𝛼
𝑆𝑟1 𝑑 + 𝐷

43. Problem 4
Constant voltage SPV plots exact
equation, approximate equation.
sr1 = 104 cm/s, sr2 = 104 cm/s,
Dn = 30 cm2/s, VSPV = 10 mV, R =0.3,
npo = 105 cm−3, d = 500 μm.
where the approximation holds for
high sr2.
The equation has a 1/α intercept
that is neither the sample thickness
d nor Ln. It is obvious from these
figures that the diffusion length
cannot be reliably determined when
Ln exceeds the sample thickness.

44. The recombination lifetime τr is
shown in Fig. and given by,
1
𝜏 𝑟𝑒𝑓𝑓
=
1
𝜏 𝐵
+
1
𝜏 𝑆
; 𝜏 𝑆 =
𝑑
2𝑠 𝑟
& 𝜏 𝐵 =
1
𝜎 𝑛 𝑣 𝑡ℎ 𝑁𝑡is plotted in Fig as a function of
impurity density NT. Determine σn
and sr .vth = 107 cm/s.
Problem 5

45. From the given equations, we can
write,
1
𝜏 𝑟𝑒𝑓𝑓
=
1
𝜏 𝐵
+
2𝑠 𝑟
𝑑
from the two points on the graph,
we can obtain two equations,
31.06 × 103 = 1016 𝜎 𝑛 + 4 × 103 𝑠 𝑟
Sr = 7.76 cm/s and 𝜎 𝑛= 9.97x10-15 cm2
Problem 5

46. 8/18/2018
THANK YOU!
Measurement Of Minority-carrier Lifetime By Time-resolve Photoluminescence By R. K. Ahrenkiel
Measurement Of Minority Carrier Lifetime In Solar Cells From Photo-induced Open-circuit Voltage Decay
By JOHN E. Mahan, Thomas W.E Kstedt,, Robert I. Frank, Member, Ieeaen,d Roy Kapiow
Minority-carrier Lifetime Measurements On Silicon Solar Cells Using Isc And Voc Transient Decay B. H.
Rose
Carrier Lifetime Analysis By Photoconductance Decay And Free Carrier Absorption Measurement H.-J.
Schulze, A. Frohnmeyer, Niedernostheide, F. Hille, P. Tutto, T. Pavelka And G. Wachutkab
Measurement Of Carrier Lifetimes In Germanium And Silicon DONALD T. Stevenson And Robert J. Keyes
Electrical And Electronic Measurements By Kaufmann
Semiconductor Material And Device Characterization By Dieter K. Schroder