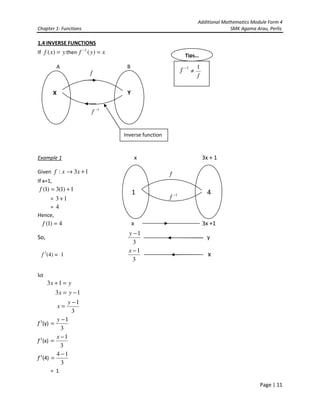
This document provides information about functions from Additional Mathematics Module Form 4. It defines relations and different ways to represent them using arrow diagrams, ordered pairs, and graphs. It explains the concepts of domain, codomain, range, objects and images. Functions are defined as a special type of relation where each object has only one image. Function notation and evaluation are demonstrated through examples. Composite functions are introduced as the combined effect of two functions gf(x). Examples are provided to show how to determine one function given information about the composite function.

1. Additional Mathematics Module Form 4
Chapter 1- Functions SMK Agama Arau, Perlis
Page | 1
CHAPTER 1- FUNCTIONS
1.1 RELATIONS
1.1.1 Representing Relations
1- By Arrow Diagram
One to one relation
x x + 2
Many to one relation
x x2
2- By Ordered Pair
(1, 3), (2, 4), (3, 5)
(1, 4), ( −2, 4), (3, 9), ( −3, 9)
3. By Graph
y (Image)
4 X
3 X
0 1 2 x (object)
One to many relation
x x
Many to many relation
360 min
3600 sec
60 sec
0.25 day
6 hours
1 min
2160 sec
1 hour
−2
2
3
−3
4
9
1
2
3
3
4
5
2
−2
3
−3
4
9

2. Additional Mathematics Module Form 4
Chapter 1- Functions SMK Agama Arau, Perlis
Page | 2
domain
codomain
A B
Set A is called domain of the relation and set B is the codomain.
Each of the elements in the domain (Set A) is an object. So 1, 2 and 3 are called object.
Each of the elements in the codomain (Set B) is an image. So 3, 4, 5 and 6 are called image.
The set that contains all the images that are matched is the range.
A B
Domain={ 1,2,3 } codomain= {3,4,5,6}
Object = 1, 2, 3 image = 3, 4, 5, 6
Range= {3, 4, 5}
Object image
1.2 FUNCTIONS
1. Function is a special relation where every object in a domain has only one image. A function is also
known as a mapping.
2. From the types of relation we have learned, only one to one relation and many to one relation are
function.
Function notation
Small letter: f, g, h or something else…
xxf 2: →
Read as function f map x onto 2x
Example:
f : x 2x
f(x) = 2x
x = 1,
f(1) = 2(1)
= 2
1
2
3
3
4
5
6
object
image
Concept:
xxf 2: →
xxf 2)( =
Look at the difference between
these two.

3. Additional Mathematics Module Form 4
Chapter 1- Functions SMK Agama Arau, Perlis
Page | 3
Example 1:
1. Given function 23: −→ xxf . Find
(a) the image of –1
f(x)= 3x – 2
f(-1) = 3(– 1) – 2
= – 3 – 2
= – 5
(b) object which has the image 4
f(x) = 3x – 2
Given that the image is 4,
So f(x) = 4
Compare and ,
Hence,
3x – 2 = 4
3x = 6
x = 2
2. Given that f(x) = px + 3 and f(4)= 5. Find the value of p.
f(x) = px + 3
If x=4,
f(4)= 4p + 3
f(4)= 5
Compare and ,
Hence,
534 =+p
24 =p
2
1
=p
If the given is object, so we are going to
find the value of image. -1 is the object
because we have to find the value of its
image.
If the given is image, so we are going to find
the value of object. 4 is the image because we
have to find the value of its object.
1
2
1 2
1
2
1 2
From the information given, we know
that 4 is the object and 5 is the image.
The both function is compared because
they are under the same function or in
other way there are having the same
object which is 4. So the value of p can be
calculated.
Remember the concept:
f : x 3x – 2 then
f(x)= 3x – 2 and when x= –1,
f(-1) = 3(– 1) – 2

4. Additional Mathematics Module Form 4
Chapter 1- Functions SMK Agama Arau, Perlis
Page | 4
Example 2:
The function g is defined by
mx
x
xg
+
=
2
)( If g(5) = 3g(2), find the value of m. Hence, find:
(a) image of 4.
(b) the value of x such that the function g is undefined.
Answer:
g(5) = 3g(2)
60 + 12m = 20 + 10m
2m = - 40
m = -20
(a)
204
)4(2
)4(
−
=g
=
2
1
−
(b) 020 =−x
20=x
EXERCISE 1.2
1. Given function f is defined by 45)( −= xxf . Find the value of x if 14)( −=xf .
2. Given that 32)( −= xxf . Find the image of 5.
3. Given that function f such that
4
32
)(
−
−
=
x
x
xf .
(i) The image of 5.
(ii ) the value of x such that the function f is undefined
4. Given the function h such that 132)( 2
++= kxxxh and 9)1( =h . Find the value of k.
5. Given the function 13: +→ xxf , find
(a) the image of 2,
(b) the value of x if f(x) = x.
6. Given the function 34: +→ xxw , find the value of p such that 23)( =pw .
7. Given the function 52: −→ xxn . Find the value of k at which kkn =)( .
mm ++
= 2
)2(2
5
)5(2
.3
m
g
+
=
5
)5(2
)5( and
m
g
+
=
5
)2(2
)2( . Replace
g(5) with
m+5
)5(2
and g(2) with
m+5
)2(2
.
Any number that is divided by zero will result
undefined or infinity. The value of denominator
cannot equal to zero because it would cause
the solution becomes undefined or infinity. To
find the value of x to make the function
undefined, the denominator must be equal to
zero.

5. Additional Mathematics Module Form 4
Chapter 1- Functions SMK Agama Arau, Perlis
Page | 5
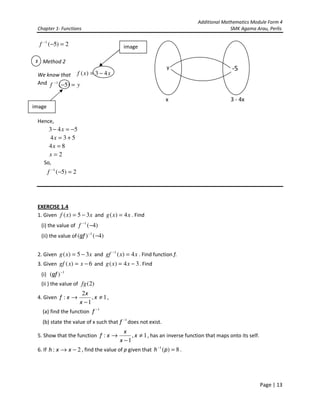
1.3 COMPOSITE FUNCTIONS
A f:x 3x B g:x x2
C
gf(x) = g[f(x)] gf
= g(3x)
= (3x)2
Example 1:
Given function 1: +→ xxf and xxg 3: → . Find the composite function gf.
f(x) = x + 1
g(x) = 3x
gf(x) = g[f(x)]
= g(x +1)
= 3(x +1)
Hence, gf: x 3(x +1)
Example 2:
The following information refers to the functions f and g.
Find
(a) the value of k,
(b) fg(x).
x
1
2
3x
3
6
(3x)2
9
36
The figure shows Set A, B and C.
The combined effect of two
functions can be represented by
the function gf(x) and not fg(x).
This is because the range of f has
become the domain of function g
or f(x) becomes the domain of
function g.
This is f(x) which has become the object of
function g
The concept is:
f(x) = 3x
f(k) = 3(k)
f(3) = 3(3)
f[g(x) ]= 3g(x)
(x +1) has become the object of function g which is
replacing x. [g(x)=3x and g(x+1)=3(x+1)]. When x in the
object is replaced by (x+1) so x in the image is also
replaced by (x+1) and become 3(x+1). We can also
expand the expression and becomes 3x + 3.
Replace f(x) with its image which is (x +1)
kx
x
xg
xxf
≠
−
→
−→
,
1
4
:
32:

6. Additional Mathematics Module Form 4
Chapter 1- Functions SMK Agama Arau, Perlis
Page | 6
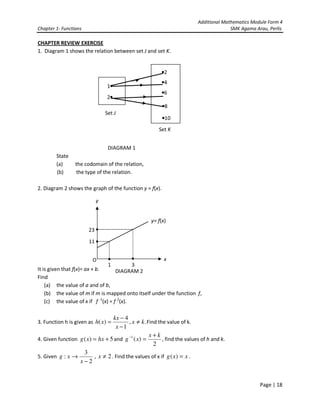
Solution:
In Form One we have learned that any number that divided by zero will result infinity or undefined.
For part (a), if there is given an expression which is a fraction there must be given an information that
the value of unknown in the denominator that it cannot be. For example, 2,
2
: ≠
−
→ x
x
h
xg . The
part of denominator is 2−x . If 2=x , the denominator would be 0 and the solution will be undefined
or infinity. So x cannot equal to 2. For the question above, we know that x cannot equal to 1 because if
1=x ,the denominator would be 0 and the solution will be undefined or infinity. It is given that kx ≠ .
We already know that 1≠x . So compare these two equations and it would result 1=k . So 1 is the
answer for part (a)
For part (b),
f(x)=2x – 3 and) 1,
1
4
)( ≠
−
= x
x
xg
fg(x) = f[g(x)]
= )
1
4
(
−x
f
= 2 )
1
4
(
−x
- 3
=
1
8
−x
- 3
=
1
)1(3
1
8
−
−
−
− x
x
x
=
1
)1(38
−
−−
x
x
=
1
338
−
+−
x
x
=
1
311
−
−
x
x
, 1≠x
Example 3:
The following information refers to the functions f and g.
2,
2
3
:
34:
≠
−
→
−→
x
x
xg
xxf
Replace g(x) with
1
4
−x
f(x)=2x – 3 ,
)
1
4
(
−x
f = 2 )
1
4
(
−x
- 3

7. Additional Mathematics Module Form 4
Chapter 1- Functions SMK Agama Arau, Perlis
Page | 7
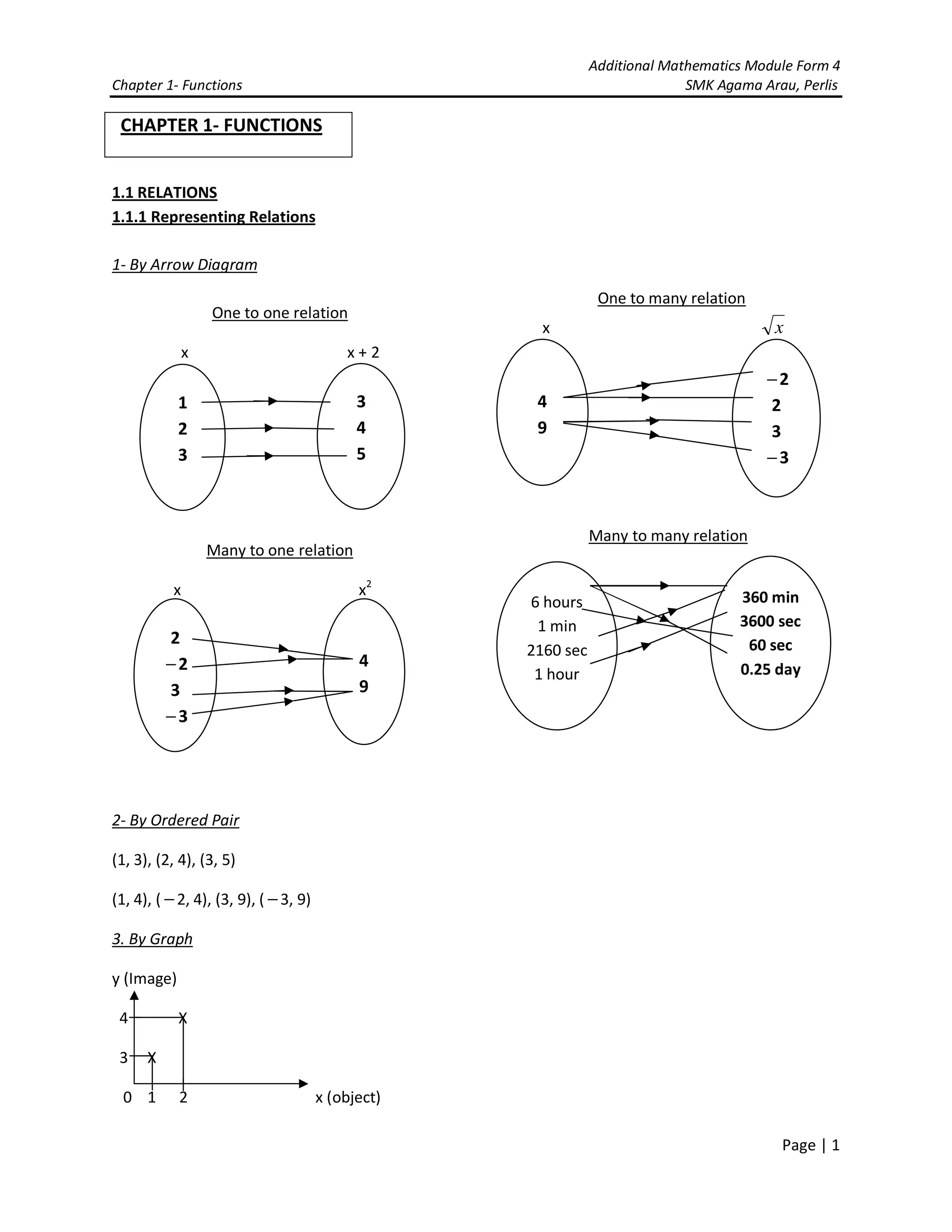
Find
(a) the value of gf(1)
(b) f2
Solution:
For part (a), at first we have to find gf(x).
Given xxf 34)( −= and 2,
2
3
)( ≠
−
= x
x
xg
gf(x)= g[f(x)]
= g(4 – 3x)
=
2)34(
3
−− x
=
x32
3
−
gf(x)=
3
2
,
32
3
≠
−
x
x
gf(1)=
)1(32
3
−
=
32
3
−
=
1
3
−
= 3−
For part (b), f2
means ff.
Given xxf 34)( −=
ff(x)= f[f(x)]
= f ]34[ x−
= )34(34 x−−
= x9124 +−
= 89 −x
89)(2
−= xxf
Replace f(x) with x34 −
2
3
)(
−
=
x
xg
2)34(
3
)34(
−−
=−
x
xg
Replace f(x) with x34 −
xxf 34)( −= ,
f ]34[ x− = )34(34 x−−

8. Additional Mathematics Module Form 4
Chapter 1- Functions SMK Agama Arau, Perlis
Page | 8
1.3.1 Determining one of the function in a given composite function
(1)The following information refers to the functions f and fg.
Find function g.
Solution:
Given 32)( −= xxf and 1,
1
311
)( ≠
−
−
= x
x
x
xfg
If 32)( −= xxf ,
If 32)( −= yyf
So 3)]([2)]([ −= xgxgf
3)]([2)( −= xgxfg
Given 1,
1
311
)( ≠
−
−
= x
x
x
xfg .
Compare the two equations.
Hence,
1
311
3)]([2
−
−
=−
x
x
xg
3
1
311
)]([2 +
−
−
=
x
x
xg
1
)1(3
1
311
)]([2
−
−
+
−
−
=
x
x
x
x
xg
1
)1(3311
)]([2
−
−+−
=
x
xx
xg
1
33311
)]([2
−
−+−
=
x
xx
xg
1
8
)]([2
−
=
x
xg
)1(2
8
)]([
−
=
x
xg
1,
1
311
:
32:
≠
−
−
→
−→
x
x
x
xfg
xxf
Remember the concept…
f(x) = 2x – 3
f(k) = 2k – 3
f(3) = 2(3) – 3
f[g(x)]= 2g(x) – 3
Simplify 8 and 2

9. Additional Mathematics Module Form 4
Chapter 1- Functions SMK Agama Arau, Perlis
Page | 9
1
4
)(
−
=
x
xg
Hence 1,
1
4
: ≠
−
→ x
x
xg
(2) The following information refers to the functions f and fg.
Find function f.
Solution:
1
311
1
4
1
311
)]([
−
−
=





−
−
−
=
x
x
x
f
x
x
xgf
Let
y
x
=
−1
4
yxy −=4
yxy += 4
y
y
x
+
=
4
Substitute and into ,
1
4
)
4
(311
)(
−
+
+
−
=
y
y
y
y
yf
=
y
y
y
y
y
y
−
+
+
−
4
)
312
(11
1,
1
311
:
1
4
:
≠
−
−
→
−
→
x
x
x
xfg
x
xg
1,
1
311
:
1
4
:
≠
−
−
→
−
→
x
x
x
xfg
x
xg
2
3
1
2 3 1
Convert 1 to a fraction

10. Additional Mathematics Module Form 4
Chapter 1- Functions SMK Agama Arau, Perlis
Page | 10
=
y
yy
y
y
y
y
−+
−
−
4
31211
=
y
y
yy
4
31211 −−
=
y
y
y
4
128 −
=
4
128 y
y
y
×
−
= 32 −y
32)( −= yyf
32)( −= xxf
EXERCISE 1.3
1. Function f and gf are given as
2
1
)(
+
=
x
xf and 23)( += xxgf respectively. Find function g.
2. Given xxf 35)( −= and xxg 4)( = . Find function fg.
3. Given 6)( −= xxgf and 34)( −= xxg . Find
(i) function f
(ii) function fg
4. Given the function xxw 23)( −= and 1)( 2
−= xxv , find the functions
(a) wv
(b) vw
5. Given the function 2: +→ xxw and kx
x
x
xv ≠
−
−
→ ,
1
12
)( ,
(a) state the value of k
(b) find
(i) wv(x)
(ii) vw(x)
Simplify
It means
y
y 128 −
divided by
y
4

11. Additional Mathematics Module Form 4
Chapter 1- Functions SMK Agama Arau, Perlis
Page | 11
1.4 INVERSE FUNCTIONS
If yxf =)( then xyf =−
)(1
A B
Example 1 x 3x + 1
Given 13: +→ xxf
If x=1,
1)1(3)1( +=f
= 13 +
= 4
Hence,
4)1( =f x 3x +1
So,
3
1−y
y
f-1
(4) = 1
3
1−x
x
let
yx =+13
13 −= yx
3
1−
=
y
x
f-1
(y)
3
1−
=
y
f-1
(x)
3
1−
=
x
f-1
(4)
3
14 −
=
= 1
41
X Y
Inverse function
1−
f
f
1
≠
Tips…
1−
f
f
1−
f
f

12. Additional Mathematics Module Form 4
Chapter 1- Functions SMK Agama Arau, Perlis
Page | 12
1.4.1 Determining the inverse function
Example 1:
Given 2,
2
5
: ≠
−
→ x
x
xg . Determine the inverse function 1−
g .
Solution:
let
y
x
=
− 2
5
52 =− yxy
yxy 25 +=
y
y
x
25 +
=
y
y
yg
25
)(1 +
=−
0,
25
)(1
≠
+
=−
x
x
x
xg
Example 2:
The function f is defined by xxf 43: −→ . Find f-1
(-5)
Method 1
Let
yx =− 43
yx −= 34
4
3 y
x
−
=
4
3
)(1 y
yf
−
=−
4
3
)(1 x
xf
−
=−
4
)5(3
)5(1 −−
=−−
f
4
8
=
1

13. Additional Mathematics Module Form 4
Chapter 1- Functions SMK Agama Arau, Perlis
Page | 13
2)5(1
=−−
f
Method 2
We know that
And
x 3 - 4x
Hence,
543 −=− x
534 +=x
84 =x
2=x
So,
2)5(1
=−−
f
EXERCISE 1.4
1. Given xxf 35)( −= and xxg 4)( = . Find
(i) the value of )4(1
−−
f
(ii) the value of )4()( 1
−−
gf
2. Given xxg 35)( −= and xxgf 4)(1
=−
. Find function f.
3. Given 6)( −= xxgf and 34)( −= xxg . Find
(i) 1
)( −
gf
(ii ) the value of )2(fg
4. Given 1,
1
2
: ≠
−
→ x
x
x
xf ,
(a) find the function 1−
f
(b) state the value of x such that 1−
f does not exist.
5. Show that the function 1,
1
: ≠
−
→ x
x
x
xf , has an inverse function that maps onto its self.
6. If 2: −→ xxh , find the value of p given that 8)(1
=−
ph .
2
image
xxf 43)( −=
yf =−−
)5(1
image
y -5

14. Additional Mathematics Module Form 4
Chapter 1- Functions SMK Agama Arau, Perlis
Page | 14
1.5 ABSOLUTE FUNCTION
Absolute function means the value of image is always positive because of the modulus sign.
Given xxg −→ 2: and y= ( )g x .Find the value of y if 3=x
y= ( )g x
= |)3(| g
= |32| −
= |1| −
= 1
1.5.1 Graph of absolute function
Example:
Given xxf −= 2)( and |)(| xfy = . Sketch the graph of |)(| xfy = for the domain 0≤ x ≤ 6. Hence
state the corresponding range of y.
|)(| xfy =
|2| x−=
Minimum value of y=0
When 2-x = 0 (2, 0)
X=2
i) x = 0
y |02| −=
|2|= (0, 2)
2=
ii) ) x = 6
y |62| −=
|4| −= (6 , 4)
4=
Then, sketch the graph using the points.
This is called modulus. Any value in the
modulus would be positive. If the number
is positive, it remains positive but it is
negative it would change to positive
when remove the modulus sign.
Minimum value of y must be zero
because of absolute value cannot be
negative so the minimum it could be is
zero.
Replace g(x) with is x−2
Replace f(x) with its image which is x−2

15. Additional Mathematics Module Form 4
Chapter 1- Functions SMK Agama Arau, Perlis
Page | 15
Y
5
4
3 |)(| xfy =
2
1
0 x
1 2 3 4 5 6
Hence, the corresponding range of y is 0≤ y ≤ 4
:: Some important information to be understood ::
1. Concept Of Solving Quadratic Equation by factorization
0432
=−− xx
0)4)(1( =−+ xx
01 =+x or 04 =−x
1−=x or 4=x
Example:
Given xxxf 52)( 2
−= . Find the possible values of k such that kf =−
)3(1
x 2x2
– 5x
Solution:
kf =−
)3(1
Hence,
352 2
=− xx
0352 2
=−− xx
0)3)(12( =−+ xx
Range of x
Range of y
3
To make a product equal to zero, one of
them or both must be equal to zero. We
do not know either x-1 is equal to zero or
x-4 equal to zero so that is why we use
the word ‘or’ not ‘and.’
The general form of quadratic equation is
02
=++ cbxax . To factorize and use the
concept, the equation must be equal to zero.
k
image
object

16. Additional Mathematics Module Form 4
Chapter 1- Functions SMK Agama Arau, Perlis
Page | 16
012 =+x or 03 =−x
2
1
−=x or 3=x
2
1
)3(1
−=−
f or 3)3(1
=−
f
Given that kf =−
)3(1
2
1
−=k or 3=k
2. Concept of Square root and any root which is multiple of 2
In lower secondary we have learned that if x2
= 4 then x = 2. Actually the right answer for it is not 2 but
2± ( 2± is +2 and -2). This is because if (2)2,
the answer is 4 and if (-2)2
, the answer is also 4. So the
square root of 4 is 2± . It is also the same for fourth root, sixth root and so on. But in certain situation,
the answer will be only one.
Example:
Solve the equation 644 2
=x .
Solution:
4
16
644
2
2
±=
=
=
x
x
x
3. Comparison method
Example:
Given the functions 2,
2
: ≠
−
→ x
x
h
xg and 0,
12
:1
≠
+
→−
x
x
kx
xg where h and k are constants,
find the value of h and of k.
Solution:
From the information given, we know that the method that we have to use to solve the question is
comparison method.
To make a product equal to zero, one of
them or both must be equal to zero. We
do not know either 2x+1 is equal to zero
or x-3 equal to zero so that is why we use
the word ‘or’ not ‘and.’

17. Additional Mathematics Module Form 4
Chapter 1- Functions SMK Agama Arau, Perlis
Page | 17
First, we have to find the inverse function of g.
Let
y
x
h
=
− 2
hyyx =− 2
yhyx 2+=
y
yh
x
2+
=
y
yh
yg
2
:1 +
→−
0,
2
:1
≠
+
→−
x
x
xh
xg
Given that
0,
12
:1
≠
+
→−
x
x
kx
xg
Both of them are inverse function of g.
So compare and ,
0,
)(
)2()(
:1
≠
+
→−
x
x
xh
xg
0,
)(
)()12(
:1
≠
+
→−
x
x
xk
xg
Hence ,
12=h and 2=k
1
2
1 2

18. Additional Mathematics Module Form 4
Chapter 1- Functions SMK Agama Arau, Perlis
Page | 18
CHAPTER REVIEW EXERCISE
1. Diagram 1 shows the relation between set J and set K.
DIAGRAM 1
State
(a) the codomain of the relation,
(b) the type of the relation.
2. Diagram 2 shows the graph of the function y = f(x).
It is given that f(x)= ax + b.
Find
(a) the value of a and of b,
(b) the value of m if m is mapped onto itself under the function f,
(c) the value of x if f -1
(x) = f 2
(x).
3. Function h is given as .,
1
4
)( kx
x
kx
xh ≠
−
−
= Find the value of k.
4. Given function 5)( += hxxg and ,
2
)(1 kx
xg
+
=−
find the values of h and k.
5. Given 2,
2
3
: ≠
−
→ x
x
xg . Find the values of x if xxg =)( .
1•
2•
•2
•4
•6
•8
•10
Set J
Set K
1 3
11
23
x
y
y= f(x)
O
DIAGRAM 2

19. Additional Mathematics Module Form 4
Chapter 1- Functions SMK Agama Arau, Perlis
Page | 19
6. Functions f and g are defined by hxxf −→ 3: and 0,: ≠→ x
x
k
xg , where h and k are
constants. It is given that f −1
(10) = 4 and fg(2) = 16. Find the value of h and of k.
7. Given that 23)( −= xxf and 1)( 2
−= xxfg , find
(i) the function g
(ii) the value of gf(3)
8 Given 22)( += xxf and |)(| xfy = . Sketch the graph of |)(| xfy = for the domain 0≤ x ≤ 4. Hence
state the corresponding range of y.
9. Given that function h is defined as 12: +→ pxxh . Given that the value of 3 maps onto itself under
the function h, find
(a) the value of p
(b) the value of )2(1
−−
hh
10. Given that the functions 12)( −= xxh and qpxxhh +=)( , where p and q are constants, calculate
(a) the value of p and q
(b) the value of m for which mh 2)1( =−
11. Function g and composite function fg are defined by 3: +→ xxg and 76: 2
++→ xxxfg .
(a) Sketch the graph of y = ( )g x for the domain −5≤ x ≤ 3.
(b) Find f(x).
12. Given quadratic function 2
( ) 2 3 2g x x x= − + . find
(a) g(3),
(b) the possible values of x if 22)( =xg
13. Functions f and g are given as 2
: xxf → and qpxxg +→: , where p and q are constants.
(a) Given that )1()1( gf = and )5()3( gf = , find the value of p and of q.
(b) By using the values of p and q obtained in (a), find the functions
(i) gg
(ii) 1−
g
14. If 63)( −= xxw and 16)( −= xxv , find
(a) )(xwv
(b) the value of x such that xxwv =− )2( .
15. Given 63)( −= xxf . Find the values of x if 3)( =xf .