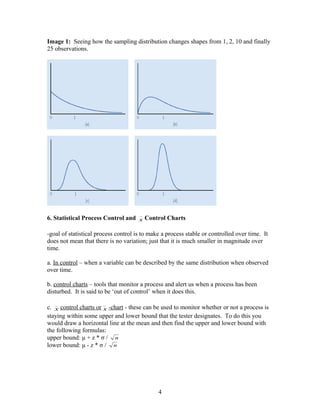
1) This document discusses sampling and sampling distributions, including key terms like population, sample, parameter, statistic, and point estimation. 2) It describes simple random sampling for both finite and infinite populations and introduces the concept of sampling distributions - the probability distributions of sample statistics. 3) The sampling distribution of the mean is discussed, including how it approaches a normal distribution as sample size increases due to the central limit theorem.

1. x
Chapter 7 _Sampling and Sampling Distributions
Recall from before that the population is the set of all elements in a study while a sample
is a subset of the population.
We also talked about statistical inference, which is when we develop estimates of the
population from sample data and infer what the population must look like. This is done
b/c:
-Population data is generally not something you can obtain
-if the sampling is good it is much quicker and easier to get the estimate and it should be
reliable
A. Terms & Types of Simple Random Samples
1. Parameter- the number and variable that describes the population. In general we
assume this to be unknown, but in some instances it is known.
2. Statistic – a value that is computed from the sample data. It comes exclusively from
sample data and is not composed of any unknown parameters.
3. Point Estimation – this is using the data from the sample to compute the value of a
sample statistic. This is what serves as an estimate for the population parameter.
a. point estimator – the estimate of the population parameter; an example is a point
x
_estimator for μ.
b. point estimate – the actual value that is computed for the point estimator
ex: = 4.7
c. sampling error – the absolute value of the difference between the point estimate and the
actual population statistic.
Formula: | point estimate – population parameter |
4. Simple Random Sample (Finite Population) – a SRS of size n from a finite
population so size in is selected from all possible samples of size n. In this case each has
an equally likely probability of being selected.
-Two ways to do this:
(a) Sampling with replacement – choose the sample and once a piece of data is chosen for
your sample you take it out of the population
(b) Sampling w/o replacement – in this instance after a piece of data is chosen for a
sample, it is put back into the population and may be chosen again at random.
5. Simple Random Sample (Infinite Population) – in this instance there are an infinite
number of population data points. To be considered an infinite population SRS it must
satisfy the following two conditions:
1

2. (a) Each element must come from the population specified  no misidentification of
population.
(b) Each element is selected independently
B. Introduction To Sampling Distributions
-if you continue to take samples of data and compute every possible combination of
samples (i.e. all permutations or combinations) of size n then the sample statistics/point
estimators can have their own distribution.
-so each sample statistic/point estimator will have its own distributions with its own
mean, variance, and standard deviation.
-we we know what type of distribution this is we can make probability statements from it
and assess how close the point estimates are to the population parameters (i.e. how close
_x
x
is to _μ)
1. Sampling Distribution – the probability distribution of any particular sampling
statistic.
2. Law of Large Numbers – if we draw observations from a population with a finite
mean μ at random, as we increase the number of observations we draw the value of the
sample mean ( ) gets closer and closer to the population mean.
x
-note _that this makes sense b/c as you increase the size of your sample it gets closer to the
size of the population. So it begins to look more and more like the population itself. For
this reason the mean should approach the population mean.
3. Sampling Distribution of - this is the probability distribution of all possible values
of a sample mean given a certain size sample n.
Ex:
-Suppose we have a distribution as follows:
If we want to create a sampling distribution we
would take samples of size n, let’s say 15
from the distribution to the right and from
each sample obtain a mean, variance,
and standard deviation.
2
x
15 20 25
Sample1-
has own
_x
, s2, &
s
Sample 2-
has own
_x
, s2, &
s

3. …..continue with process for all possible samples of size 15. If we do this we can take
the values from each sample and create its own distribution as shown below.
Graphically:
-notice now we have a distribution of sample means.
This distribution is created from the means of each
sample and it has its own variance and standard
deviation. Note that they should be much
smaller than the distribution sampled
from since we created it from the sample
means of the data.
4. Characteristics of the Sampling Distribution of a. E ( ) = μ  so the mean of all values of x
x
__x
_should be the population mean μ. This is
x
_called unbiasedness. Since the value of the sampling statistic converges to the population
parameter.
b. Standard Deviation of - called the standard error of the mean  it tells us how close
our estimates of the mean are to the actual mean.
i. finite population value – σ _x
= (N -n) /(N -1) * (σ / n )
ii. infinite population - σ _x
= σ / n
x
note: σ _= population variance, N = population size, n = sample size; must still use the
infinite population estimate if n/N < 5% of the population size.
5. Central Limit Theorem – when choosing n and it is a SRS we can assume that the
sampling distribution of ~N as N gets larger and larger. If it is greater than 30 we
assume it is Normal.
-if the population is normal, then the sampling distribution must be normal and this rule
does not apply. This is for any size of sample.
-as n increases the variance and standard deviation get tighter and there is a higher
probability that the sample means is within a certain distance of the actual population
mean.
3
_x
20

4. Image 1: Seeing how the sampling distribution changes shapes from 1, 2, 10 and finally
25 observations.
6. Statistical Process Control and _x
Control Charts
-goal of statistical process control is to make a process stable or controlled over time. It
does not mean that there is no variation; just that it is much smaller in magnitude over
time.
a. In control – when a variable can be described by the same distribution when observed
over time.
b. control charts – tools that monitor a process and alert us when a process has been
disturbed. It is said to be ‘out of control’ when it does this.
c. _x
control charts or _x-chart - these can be used to monitor whether or not a process is
staying within some upper and lower bound that the tester designates. To do this you
would draw a horizontal line at the mean and then find the upper and lower bound with
the following formulas:
upper bound: μ + z * σ / n
lower bound: μ - z * σ / n
4

5. Note: that the tester determines how far away is acceptable in this process. It could be 3
standard deviations (z’s) or it could be less. It depends on what is designated as a stable
process over time.
Graphically:
Upper bound
Lower bound
x
_Note: as long as the sample points stay within the red-lines the process is ‘in control.’ As
soon as you obtain a measurement that puts it outside of the upper and lower bounds the
process has been disturbed somehow and needs to be adjusted to put it back on a steady
path.
7. Unbiasedness and Minimum Variance Estimates
a. Unbiasedness – In general we say that a sampling statistic in unbiased if its sampling
distribution value converges to the population value.
i.  μ so it is an unbiased estimator.
ii. s2  σ2 so it is also an unbiased estimator.
b. Minimum variance estimate – since the sampling distribution of _x
produces the
smallest variances estimate of all possible other values that could estimate the mean (like
median, mode, or any estimator). So we way it is MVE or the minimum variance
estimator.
C. Inference about a Population Proportion
Now we are concerned with finding out and exploring proportions. Many of the
techniques and statistics that we have used in previous chapters will be used again. So it
should seem very familiar how we go about studying and analyzing this type of
procedure. Just make sure to note the definition of a proportion below.
1. Proportion – this is the percentage that our population takes on a certain
characteristic.
p = number of successes / total individuals
5
μ
sample
Distance = -z * σ / n

6. = this is the sample proportion and is designated at p-hat. It is an actual calculated
value.
Example: Number of students who passed a class out of 20. If we let passing be greater
than 70% and we find that 14 students had scores greater than 70% then our is:
= 14 / 20 = 0.70
2. Sampling Distribution of p:
Just as with the mean we had a sampling distribution that had certain characteristics, we
can also note that p also has the following characteristics.
a. The expected value or mean of the sampling distribution is p (i.e. the population
proportion)
so E( ) = p
b. The standard deviation of p or =
c. graphically: We can use this just as before with our z. So if we assume that we have a
normal distribution with a large enough sample size then our Z becomes:
Z = ) /
So if we were given that p = 0.60 and n = 36 and wanted to know the P ( . We
can calculate our Z = (0.53 – 0.60) / 0.0816 = -0.86 where = ≈0.0816.
So this is the same as asking P (Z < -0.86) = 0.1949
6
So from our Z-table we find this
value is 0.1949 or about 19.49%
Z
-0.857
Z

7. = this is the sample proportion and is designated at p-hat. It is an actual calculated
value.
Example: Number of students who passed a class out of 20. If we let passing be greater
than 70% and we find that 14 students had scores greater than 70% then our is:
= 14 / 20 = 0.70
2. Sampling Distribution of p:
Just as with the mean we had a sampling distribution that had certain characteristics, we
can also note that p also has the following characteristics.
a. The expected value or mean of the sampling distribution is p (i.e. the population
proportion)
so E( ) = p
b. The standard deviation of p or =
c. graphically: We can use this just as before with our z. So if we assume that we have a
normal distribution with a large enough sample size then our Z becomes:
Z = ) /
So if we were given that p = 0.60 and n = 36 and wanted to know the P ( . We
can calculate our Z = (0.53 – 0.60) / 0.0816 = -0.86 where = ≈0.0816.
So this is the same as asking P (Z < -0.86) = 0.1949
6
So from our Z-table we find this
value is 0.1949 or about 19.49%
Z
-0.857
Z