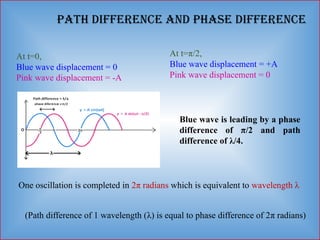
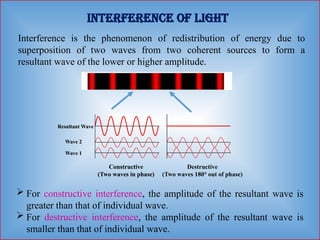
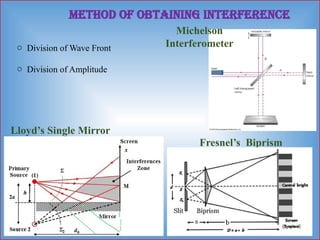
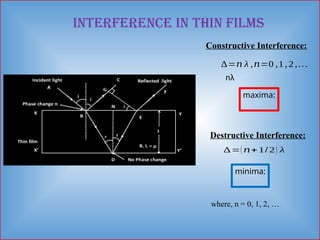
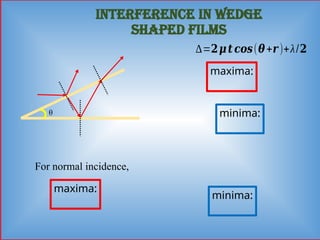
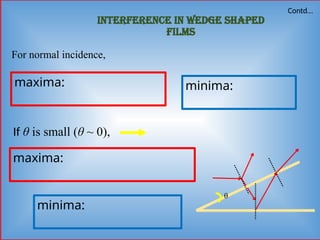
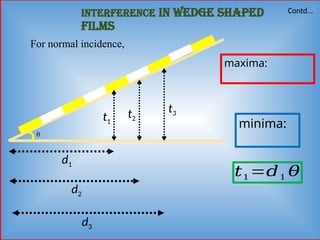
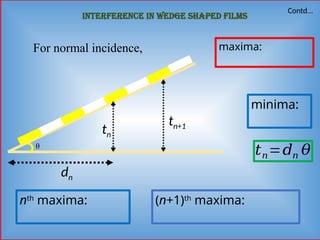
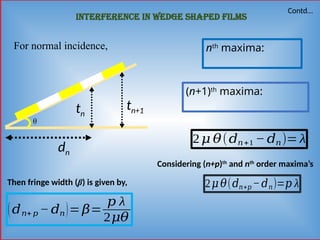
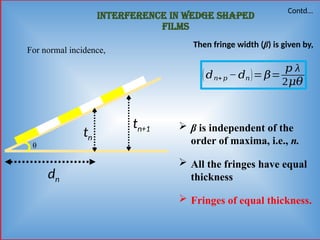
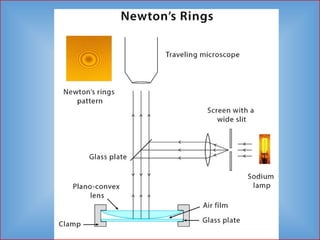
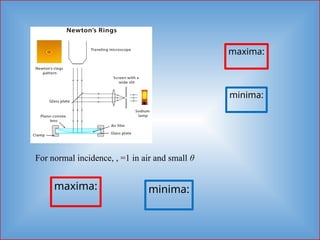
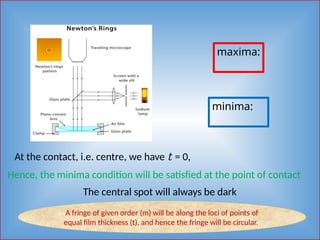
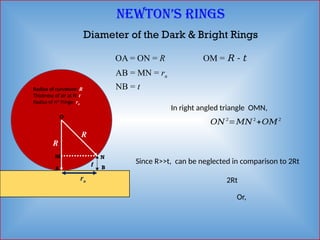
Detailed informative notes on "Interference" including Path difference, phase difference, coherent sources, methods to obtain coherent sources, sustained interference, interference due to thin films, interference due to wedge shaped films, Newton's rings, Applications

1. Fundamentals
Of
Interference
Dr. Priyanka Nayak
Assistant Professor
AIAS (Physics)

2. Index
 Path difference and Phase difference
 Coherent Sources
 Conditions for Coherent Sources
 Interference
 Types of Interference
 Sustained Interference
 Methods for Obtaining Interference
 Newton’s Rings Experiment

3. Path Difference and Phase Difference
At t=0,
Blue wave displacement = 0
Pink wave displacement = -A
At t=π/2,
Blue wave displacement = +A
Pink wave displacement = 0
Blue wave is leading by a phase
difference of π/2 and path
difference of λ/4.
One oscillation is completed in 2π radians which is equivalent to wavelength λ
(Path difference of 1 wavelength (λ) is equal to phase difference of 2π radians)

4. Coherence
Partial Coherence
Incoherence
Coherence

5. Coherent Sources
• Two wave sources are perfectly coherent if they have a constant phase
difference and the same frequency.
• Coherent sources are those which emit light waves of same wavelength or
frequency and have a constant phase difference.
• It is the ideal property of waves which enables interference.

6. Conditions for coherent Sources
o Coherent sources are obtained from single source.
o The source must emit monochromatic light.
o The path difference between light sources must be
very small.
Why can’t two sources behave as coherent
sources?

7. Interference of Light
Interference is the phenomenon of redistribution of energy due to
superposition of two waves from two coherent sources to form a
resultant wave of the lower or higher amplitude.
Wave 1
Wave 2
Resultant Wave
Constructive
(Two waves in phase)
Destructive
(Two waves 180° out of phase)
Wave 1
Wave 2
Resultant Wave
Constructive
(Two waves in phase)
 For constructive interference, the amplitude of the resultant wave is
greater than that of individual wave.
 For destructive interference, the amplitude of the resultant wave is
smaller than that of individual wave.

8. Sustained Interference
The interference pattern in which dark and bright fringes positions are
fixed on the screen is known as sustained interference.
Conditions:
 The sources must be monochromatic.
 The two sources must emit waves of same frequency.
 The two sources must be coherent.
 The two coherent sources must be very close to each other.
 Reasonable distance must be maintained between the source and
screen.
 The amplitudes of the two interfering waves must be equal.
 The coherent sources must be narrow.

9. o Division of Wave Front
o Division of Amplitude
Method of Obtaining Interference
Lloyd’s Single Mirror
Fresnel’s Biprism
Michelson
Interferometer

10. • Division of Wave Front
 This method uses multiple slits, lenses, prisms or mirrors for dividing a
single wavefront laterally to form two smaller segments that can
interfere with each other.
 In the division of a wavefront, the interfering beams of radiation that
left the source in different directions and some optical means is used to
bring the beams back together.
 This method is useful with small sources.
 Double slit experiment, Fresnel’s biprism are excellent example of
interference by division of wavefront.
Method of Obtaining Interference

11. • Division of Amplitude
 The method, which is used to produce two coherent sources from a
common source, is called division of amplitude that maintains the same
width but reduced amplitude.
 After following different paths the two waves of reduced amplitudes are
combined to produce an interference pattern. In this method, the
interfering beams consist of radiation that has left the source in the same
direction. This radiation is divided after leaving the source and later
combined to produce interference.
 This method can be used with extended sources.
 Michelson interferometer is an example of interference by division of
amplitude.
Method of Obtaining Interference

12. Interference in Thin Parallel Films
If a plane wave falls on a thin film, partial reflection and partial refraction
occur from the top surface of the film. The refracted beam travels in the
medium and again suffers partial reflection and refraction at the bottom
surface of the film. In this way several reflected and refracted rays are
produced by a single incident ray. These waves superimpose on each other
and produce interference patterns.
In short, the wave reflected from the upper surface interferes with the wave
reflected from the lower surface. Such studies have many practical applications
and also explain phenomena such as the formation of beautiful colors produced
by a soap film illuminated by white light.

13. Let us estimate the optical path difference (Δ) between
BC & EF
Optical path difference = (BD+DE)in film – BGin air
Δ = 𝝁(BD+DE) - BG
In ΔBDN, BD DE BD+DE
In ΔBEG, BG= (BN+NE) sin i
In ΔBDN, BN = NE
BG= 2
𝑠𝑖𝑛𝑖=𝜇sin 𝑟
BG= 2
∆=
2 𝜇𝑡
cos𝑟
−2 𝑡 𝜇
𝑠𝑖𝑛2
𝑟
cos𝑟
=
2 𝜇𝑡
cos𝑟
(1 − 𝑠𝑖𝑛
2
𝑟 )=2 𝜇𝑡 cos 𝑟
Since reflected waves suffers a phase shift of π, we must add λ/2 in the path difference

14. maxima:
minima:
Interference in thin films
Constructive Interference:
∆=𝑛 λ ,𝑛=0 ,1,2,…
nλ
Destructive Interference:
∆=(𝑛+ 1/2) λ
where, n = 0, 1, 2, …

15. Interference in wedge
shaped films
θ
maxima:
minima:
For normal incidence,
maxima:
minima:
∆=𝟐𝝁𝒕𝒄𝒐𝒔(𝜽+𝒓)+λ/𝟐

16. Interference in wedge shaped
films
For normal incidence,
maxima: minima:
If θ is small (θ ~ 0),
maxima:
Contd…
θ
minima:

17. Interference in wedge shaped
films
maxima:
minima:
For normal incidence,
𝑡1 =𝑑1 𝜃
θ
t1
t2
t3
d1
d2
d3
Contd…

18. Interference in wedge shaped films
θ
maxima:
minima:
tn
tn+1
For normal incidence,
nth
maxima:
dn
𝑡𝑛=𝑑𝑛 𝜃
(n+1)th
maxima:
Contd…

19. Interference in wedge shaped films
θ
tn
tn+1
For normal incidence, nth
maxima:
dn
(n+1)th
maxima:
2𝜇 𝜃(𝑑𝑛+1 − 𝑑𝑛)= λ
2𝜇 𝜃(𝑑𝑛+𝑝 −𝑑𝑛)=𝑝 λ
Considering (n+p)th
and nth
order maxima’s
(𝑑𝑛+ 𝑝 − 𝑑𝑛)= 𝛽=
𝑝 λ
2𝜇𝜃
Then fringe width (β) is given by,
Contd…

20. Interference in wedge shaped
films
θ
tn
tn+1
For normal incidence,
dn
(𝑑𝑛+ 𝑝 −𝑑𝑛)= 𝛽=
𝑝 λ
2𝜇𝜃
Then fringe width (β) is given by,
 β is independent of the
order of maxima, i.e., n.
 All the fringes have equal
thickness
 Fringes of equal thickness.
Contd…

21. Newton’s Rings

23. maxima:
minima:
For normal incidence, , =1 in air and small θ
maxima: minima:

24. maxima:
minima:
At the contact, i.e. centre, we have t = 0,
Hence, the minima condition will be satisfied at the point of contact
The central spot will always be dark
A fringe of given order (m) will be along the loci of points of
equal film thickness (t), and hence the fringe will be circular.

25. Newton’s Rings
Diameter of the Dark & Bright Rings
R
R
O
A
N
M
t
Radius of curvature: R
Thickness of air at N: t
Radius of nth
fringe: rn
B
rn
OA = ON = R
AB = MN = rn
NB = t
OM = R - t
𝑂𝑁2
=𝑀𝑁2
+𝑂𝑀2
Since R˃˃t, can be neglected in comparison to 2Rt
In right angled triangle OMN,
2Rt
Or,

26. 𝑟𝑛
2
=𝑅 × 2𝑡 ...(1)
For Bright Rings,
2𝑡=(𝑛−
1
2 )λ
Substituting value of 2t from equation 1,
𝑟𝑛
2
=𝑅×(𝑛−
1
2)λ
𝑟𝑛
2
=𝑅× (2𝑛−1) λ/2
(𝐷𝑛
2 )
2
=𝑅×(2𝑛−1) λ/2
𝐷𝑛
2
=2 λ 𝑅(2𝑛−1)
𝐷𝑛=√2 𝜆 𝑅(2𝑛−1)
For Dark Rings,
2𝑡=𝑛 λ
𝑟𝑛
2
=𝑛 λ 𝑅
(𝐷𝑛
2 )
2
=𝑛𝑅 λ
(𝐷𝑛)2
=4 𝑛𝑅 λ
𝐷𝑛=√4𝑛𝑅 𝜆
𝑫𝒏∝√(𝟐𝒏−𝟏)
𝑫𝒏∝√𝒏
Diameter of the Dark & Bright Rings

27. Applications of Newton’s Ring
I. Determination of Wavelength (λ) of a Monochromatic
Light
Diameter of nth
order dark fringe in Newton’s ring method is
Diameter of (n+p)th
order dark fringe in Newton’s ring method is
(1)
(2)
Subtracting equation (1) from (2), we have
λ=
𝐷(𝑛+ 𝑝)
2
− 𝐷𝑛
2
4 𝑝𝑅

28. II. Determination of Refractive Index () of a Liquid
Diameter of nth
order dark fringe in air film is
(3)
Diameter of nth
order dark fringe in liquid film is
(4)
Taking the ration of equation (3) and (4), we have
𝝁=
[ 𝐷𝑛
2
]𝑎𝑖𝑟
[𝐷𝑛
2
]𝑙𝑖𝑞𝑢𝑖𝑑