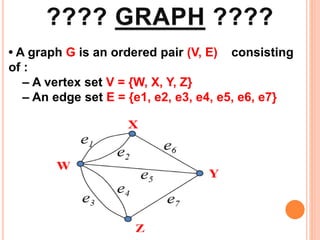
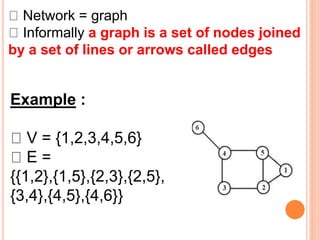
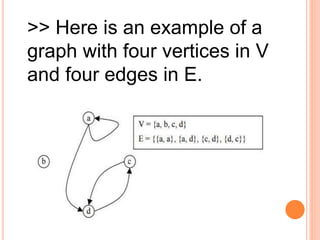
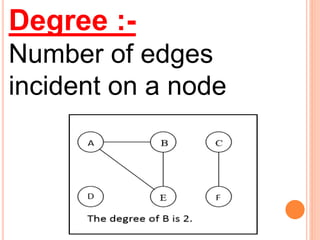
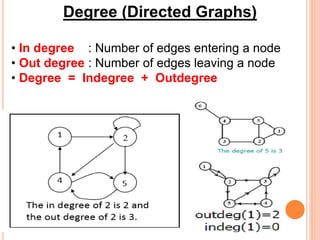
This document defines and provides examples of different types of graphs and digraphs. It defines a graph as an ordered pair of vertices and edges, and defines a digraph as a graph where edges have a direction from one vertex to another. It provides examples of simple, symmetric, asymmetric, complete, and balanced digraphs. It also defines in-degree, out-degree, and total degree of vertices in digraphs.

3. • A graph G is an ordered pair (V, E) consisting
of :
– A vertex set V = {W, X, Y, Z}
– An edge set E = {e1, e2, e3, e4, e5, e6, e7}

4. Network = graph
Informally a graph is a set of nodes joined
by a set of lines or arrows called edges
Example :
V = {1,2,3,4,5,6}
E =
{{1,2},{1,5},{2,3},{2,5},
{3,4},{4,5},{4,6}}

5. DIRECTED GRAPH :-
A directed graph (or digraph, or just graph) is a set
of vertices, V, together with a set of ordered pairs, E,
of edges. Thus we write that a graph,
G = (V,E)
Each edge consists of two vertices in V and is
represented diagrammatically by an arrow from
the first vertex to the second.
This definition permits self - loops, i.e., edges of
the form {v, v}, that begin and end at the same place
. Parallel edges, i.e., two identical edges in E, are
prohibited however.

6. >> Here is an example of a
graph with four vertices in V
and four edges in E.

7.  Simple Digraphs :-
A digraph that has no self-loop or
parallel edges is called a simple digraph.
Asymmetric Digraphs :-
Digraphs that have at most one
directed edge between a pair of
vertices , but are allowed to have self –
loops , are called asymmetric or
antisymmetric.

8. Symmetric Digraphs :-
Digraphs in which for every edge (a,b) (
i.e., from vertex a to b ) there is also an edge
(b,a).
 NOTE :- A digraph that is both simple and
symmetric is called a simple symmetric
digraph.
NOTE :- A digraph that is both simple and
asymmetric is called a simple asymmetric
digraph.

9. Complete Digraphs :-
1) Complete symmetric digraph..
2) Complete asymmetric digraph
1. Complete Symmetric Digraph :-
complete symmetric digraph is a simple digraph in
which there is exactly one edge directed from every vertex to
every other vertex.
2. Complete Asymmetric Digraph :-
complete asymmetric digraph is an asymmetric
digraph in which there is exactly one edge between every pair
of vertices.
 Balanced Digraphs :-
A digraph is said to be balanced if for every vertex
v , the in-degree equals to out-degree.

10. Degree :-
Number of edges
incident on a node

11. Degree (Directed Graphs)
• In degree : Number of edges entering a node
• Out degree : Number of edges leaving a node
• Degree = Indegree + Outdegree

12. Degree: Simple Facts
• If G is a graph with m edges, then
Σ deg(v) = 2m = 2 |E |
• If G is a digraph with m edges, then
Σ indeg(v) = Σ outdeg(v) = m = |E |
– Number of Odd degree Nodes is
even