This chapter discusses searching and sorting algorithms for arrays and strings. It covers sequential search, binary search, bubble sort, selection sort, and insertion sort. It also discusses using the Vector class to implement dynamic arrays and provides examples of searching voter data and converting strings to pig latin.

1. Java Programming: From Problem Analysis to Program Design, 3e Chapter 10 Applications of Arrays (Searching and Sorting) and Strings

2. Chapter Objectives Learn how to implement the sequential search algorithm Explore how to sort an array using bubble sort, selection sort, and insertion sort algorithms Learn how to implement the binary search algorithm Become aware of the class Vector Learn more about manipulating strings using the class String

3. List Processing List: a set of values of the same type Basic operations performed on a list Search list for given item Sort list Insert item in list Delete item from list

4. Search Necessary components to search a list Array containing the list Length of the list Item for which you are searching After search completed If item found, report “success,” return location in array If item not found, report “failure”

5. Search (continued) Suppose that you want to determine whether 27 is in the list First compare 27 with list[0] ; that is, compare 27 with 35 Because list[0] ≠ 27 , you then compare 27 with list[1] Because list[1] ≠ 27 , you compare 27 with the next element in the list Because list[2] = 27 , the search stops This search is successful

6. Search (continued) Let’s now search for 10 The search starts at the first element in the list; that is, at list[0] Proceeding as before, we see that this time the search item, which is 10 , is compared with every item in the list Eventually, no more data is left in the list to compare with the search item; this is an unsuccessful search

7. Search (continued)

8. Search (continued)

9. Search (continued) Using a while (or a for ) loop, the definition of the method seqSearch can also be written without the break statement as:

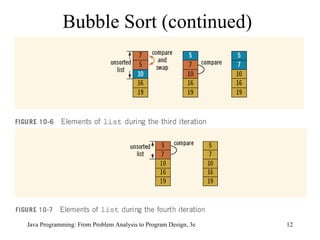
10. Sorting a List Bubble sort Suppose list[0...n - 1] is a list of n elements, indexed 0 to n - 1 We want to rearrange; that is, sort, the elements of list in increasing order The bubble sort algorithm works as follows: In a series of n - 1 iterations, the successive elements, list[index] and list[index + 1] of list are compared If list[index] is greater than list[index + 1] , then the elements list[index] and list[index + 1] are swapped, that is, interchanged

11. Bubble Sort

12. Bubble Sort (continued)

13. Bubble Sort (continued)

14. Bubble Sort (continued) It is known that for a list of length n , on average bubble sort makes n ( n – 1) / 2 key comparisons and about n ( n – 1) / 4 item assignments Therefore, if n = 1000, then to sort the list bubble sort makes about 500,000 key comparisons and about 250,000 item assignments

15. Selection Sort List is sorted by selecting list element and moving it to its proper position Algorithm finds position of smallest element and moves it to top of unsorted portion of list Repeats process above until entire list is sorted

16. Selection Sort (continued)

17. Selection Sort (continued)

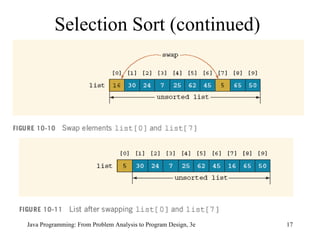
18. Selection Sort (continued) public static void selectionSort( int [] list, int listLength) { int index; int smallestIndex; int minIndex; int temp; for (index = 0; index < listLength – 1; index++) { smallestIndex = index; for (minIndex = index + 1; minIndex < listLength; minIndex++) if (list[minIndex] < list[smallestIndex]) smallestIndex = minIndex; temp = list[smallestIndex]; list[smallestIndex] = list[index]; list[index] = temp; } }

19. It is known that for a list of length n , on an average selection sort makes n ( n – 1) / 2 key comparisons and 3( n – 1) item assignments Therefore, if n = 1000, then to sort the list selection sort makes about 500,000 key comparisons and about 3000 item assignments Selection Sort (continued)

20. Insertion Sort The insertion sort algorithm sorts the list by moving each element to its proper place

21. Insertion Sort (continued)

22. Insertion Sort (continued)

23. Insertion Sort (continued)

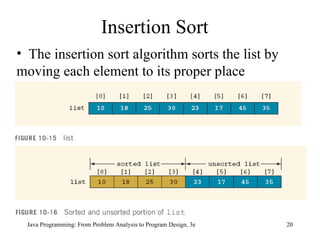
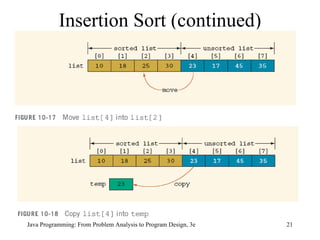
24. Insertion Sort (continued) public static void insertionSort( int [] list, int listLength) { int firstOutOfOrder, location; int temp; for (firstOutOfOrder = 1; firstOutOfOrder < listLength; firstOutOfOrder++) if (list[firstOutOfOrder] < list[firstOutOfOrder - 1]) { temp = list[firstOutOfOrder]; location = firstOutOfOrder; do { list[location] = list[location - 1]; location--; } while(location > 0 && list[location - 1] > temp); list[location] = temp; } } //end insertionSort

25. Insertion Sort (continued) It is known that for a list of length n , on average, the insertion sort makes ( n 2 + 3 n – 4) / 4 key comparisons and about n ( n – 1) / 4 item assignments Therefore, if n = 1000, then to sort the list, the insertion sort makes about 250,000 key comparisons and about 250,000 item assignments

26. Sequential Ordered Search public static int seqOrderedSearch( int [] list, int listLength, int searchItem) { int loc; //Line 1 boolean found = false ; //Line 2 for (loc = 0; loc < listLength; loc++) //Line 3 if (list[loc] >= searchItem) //Line 4 { found = true ; //Line 5 break ; //Line 6 } if (found) //Line 7 if (list[loc] == searchItem) //Line 8 return loc; //Line 9 else //Line 10 return -1; //Line 11 else //Line 12 return -1; //Line 13 }

27. Binary Search Can only be performed on a sorted list Uses divide and conquer technique to search list

28. Binary Search Algorithm Search item is compared with middle element of list If search item < middle element of list, search is restricted to first half of the list If search item > middle element of list, search second half of the list If search item = middle element, search is complete

29. Binary Search Algorithm (continued) Determine whether 75 is in the list

30. Binary Search Algorithm (continued)

31. Binary Search Algorithm (continued) public static int binarySearch( int [] list, int listLength, int searchItem) { int first = 0; int last = listLength - 1; int mid; boolean found = false ; while (first <= last && !found) { mid = (first + last) / 2; if (list[mid] == searchItem) found = true ; else if (list[mid] > searchItem) last = mid - 1; else first = mid + 1; } if (found) return mid; else return –1; } //end binarySearch

32. Binary Search Algorithm (continued)

33. Binary Search Algorithm (continued)

34. Performance of the Binary Search

35. Performance of the Binary Search (continued)

36. Performance of the Binary Search (continued) Suppose that L is a list of size 1000000 Since 1000000  1048576 = 220, it follows that the while loop in binary search will have at most 21 iterations to determine whether an element is in L Every iteration of the while loop makes two key (that is, item) comparisons

37. Performance of the Binary Search (continued) To determine whether an element is in L , binary search makes at most 42 item comparisons On the other hand, on average, a sequential search will make 500,000 key (item) comparisons to determine whether an element is in L In general, if L is a sorted list of size n , to determine whether an element is in L , the binary search makes at most 2log2 n + 2 key (item) comparisons

38. Vectors The class Vector can be used to implement a list Unlike an array, the size of a Vector object can grow/shrink during program execution You do not need to worry about the number of data elements in vector

39. Members of the class Vector

40. Members of the class Vector (continued)

41. Members of the class Vector (continued)

42. Members of the class Vector (continued)

43. Members of the class Vector (continued)

44. Vectors (continued) Every element of a Vector object is a reference variable of the type Object To add an element into a Vector object Create appropriate object Store data into object Store address of object holding data into Vector object element

45. Vector<String> stringList = new Vector<String>(); stringList.addElement(&quot;Spring&quot;); stringList.addElement(&quot;Summer&quot;); stringList.addElement(&quot;Fall&quot;); stringList.addElement(&quot;Winter&quot;); Vectors (continued)

46. Programming Example: Election Results Input: two files File 1: candidates’ names File 2: voting data Voting Data Format candidate_name region# number_of_votes_for_this_candidate

47. Programming Example: Election Results (continued) Output: election results in a tabular form Each candidate’s name Number of votes each candidate received in each region Total number of votes each candidate received

48. Programming Example: Election Results (Solution) The solution includes: Reading the candidates’ names into the array candidateName A two-dimensional array consisting of the votes by Region An array consisting of the total votes parallel to the candidateName array

49. Programming Example: Election Results (Solution) (continued) The solution includes (continued): Sorting the array candidatesName Processing the voting data Calculating the total votes received by each candidate Outputting the results in tabular form

50. Programming Example: Election Results

51. Programming Example: Election Results (continued)

52. Additional String Methods

53. Additional String Methods (continued)

54. Additional String Methods (continued)

55. Additional String Methods (continued)

56. Effects of Some String Methods

57. Programming Example: Pig Latin Strings If string begins with a vowel, ″ -way ″ is appended to it If first character is not a vowel: Add ″ - ″ to end Rotate characters until the first character is a vowel Append ″ ay ″ Input: string Output: string in pig Latin

58. Programming Example: Pig Latin Strings (Solution) Methods: isVowel , rotate , pigLatinString Use methods to: Get the str ing ( str ) Find the pig Latin form of str by using the method pigLatinString Output the pig Latin form of str

59. Programming Example: Pig Latin Strings (Sample Runs)

60. Chapter Summary Lists Searching lists Sequential searching Sequential searching on an order list Binary Search Sorting lists Bubble Sort Selection Sort Insertion Sort

61. Chapter Summary (continued) Programming examples The class Vector Members of the class Vector The class String Additional methods of the class String