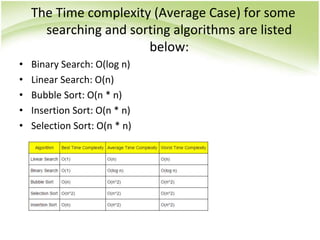
Linear search is a sequential search algorithm that checks each element of an array until the target element is found. It has a worst-case time complexity of O(n) where n is the number of elements. Binary search is a divide and conquer algorithm that compares the target to the middle element of a sorted array, eliminating half of the remaining elements with each comparison. It has a time complexity of O(log n). Common sorting algorithms like bubble sort, insertion sort, and selection sort have a time complexity of O(n^2) as they may require up to n^2 comparisons in the worst case.

1. Searching and Sorting

2.  Linear search Is the process to find whether a number is present in an array.
If it's present, then at what location it occurs.
 It is also known as a sequential search.
 It is straightforward and compare each element with the element to search
until we find it or the list ends.
 Best case: When element is found at first position in array
No. of comparisons=1
 Worst case; When element is found at last position in array
No. of comparisons=n(no. of elements )
 Average case: When element is found in middle of array
No. of comparisons=n/2(no. of elements/2 )
Linear Search

3. Linear Search
• Check every element in the list, until the
target is found
• For example, our target is 38:
i 0 1 2 3 4 5
a[i] 25 14 9 38 77 45
If item to search=38 ,then it tells found at
location 4
If item to search=55 ,then it tells Item Not found

4. Program to perform Linear Search
void linearsearch(int array[],item,n)
{
for (i = 0; i < n; i++)
{
if (array[i] == item) /* If required element is found */
{
printf(“Found at location %d”, i+1);
flag=1
break;
}
}
if (flag==0)
printf(“Item not found”);
}

5. Explanation
• Assume array of size n and item to search
• Assume initially flag=0
• First, we have to traverse the array elements using
a for loop.
• In each iteration of for loop, compare the search element
with the current array element,
– If array[i]==item, then it displays found at the position
of the corresponding array element and sets flag=1.
– If the element does not match, then move to the next
element.
• If flag==0 that means there is no match found in the given
array , then it displays not found

6. Binary Search
• Binary Search is a searching approach for finding an
element in a sorted array.
• Binary search follows the divide and conquer
approach in which the array is divided into two
halves, and the item is compared with the middle
element of an array.
• If the match is found then, the location of the middle
element is returned.
• Otherwise, we search into either of the halves
depending upon the result produced through the
match.

7. Binary Search
int BinarySearch(int key, int arr[], int n)
{
int low, high, mid;
low = 0;
high = n – 1;
while ( low <= high) {
mid = (low + high) / 2;
if ( key== arr[mid])
return mid; /*found match,return position where it is found*/
else if (key > arr[mid])
low = mid + 1; //search on right half by updating low
else
high = mid – 1; //search on left half by updating high
}
return –1; /*No match ,so return -1*/
}

8. Binary Search Explanation
• Assume key is element to search in array arr of size n
• Set two variables low=0 and high=n-1 pointing to start and
end of array
• Find the middle position of array ,mid=(low+high)/2
• Compare the middle element of the array with the key to
search.
– If the key ==arr[mid], then process is terminated and display found at
middle location.
– If the key is not found at middle element, choose which half will be
used as the next search space.
• If the key > arr[mid], then the right side is used for next search.
• If the key < arr[mid], then the left side is used for next search.
• This process is continued until the key is found or the complete
array is exhausted.

9. Example
Let us assume element to search ,key=4
Step1: Intialize two pointers of array,low=0 and
high=n-1
Step2: Find the location of middle element of
the array ie. mid=(low + high)/2 ,

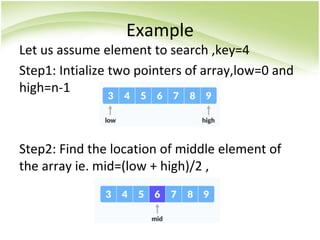
10. Example
Step3: As key <arr[mid] so it has to search on
left of array.So it update,low=0 and high=mid-1
Step4:Now new middle position=(low+high)/2=1
Step5: Then,it compares key with middle
element .As key==arr[mid],so it displays found
at middle location 1

11. Sorting – Example
11
• Original list:
– 10, 30, 20, 80, 70, 10, 60, 40, 70
• Sorted in non-decreasing order:
– 10, 10, 20, 30, 40, 60, 70, 70, 80
• Sorted in non-increasing order:
– 80, 70, 70, 60, 40, 30, 20, 10, 10

12. Sorting Problem
12
Unsorted list
• What do we want :
- Data to be sorted in order
x:
0 size-1
Sorted list

13. • Suppose we need to sort in ascending order...
• Repeatedly check adjacent pairs sequentially,
swap if not in correct order
• Example:
• The last number is always the largest
Bubble Sort
9 20 11
18 45
77
Incorrect order, swap!
Correct order, pass!

14. Bubble Sort
• Fix the last number, do the same procedures
for first N-1 numbers again...
• Fix the last 2 numbers, do the same
procedures for first N-2 numbers again...
• ...
• Fix the last N-2 numbers, do the same
procedures for first 2 numbers again...

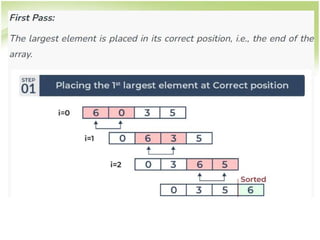
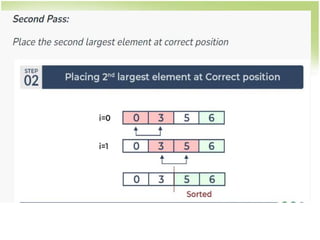
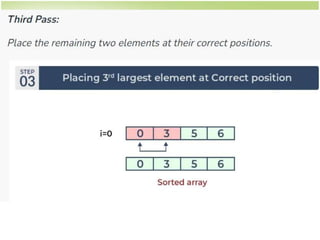
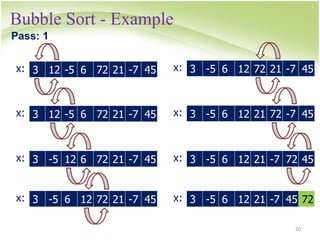
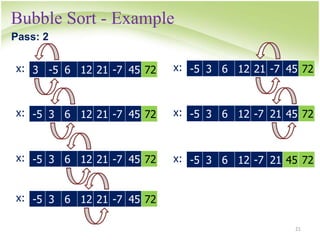
15. Bubble Sort
for i -> 1 to n-1
for j -> 1 to n-i
if a[j]>a[j+1], swap them
• How to swap?

19. Bubble Sort
19
How the passes proceed?
• In pass 1, we consider index 0 to n-1.
• In pass 2, we consider index 0 to n-2.
• In pass 3, we consider index 0 to n-3.
• ……
• ……
• In pass n-1, we consider index 0 to 1.

20. Bubble Sort - Example
20
3 12 -5 6 72 21 -7 45
x:
Pass: 1
3 12 -5 6 72 21 -7 45
x:
3 -5 12 6 72 21 -7 45
x:
3 -5 6 12 72 21 -7 45
x:
3 -5 6 12 72 21 -7 45
x:
3 -5 6 12 21 72 -7 45
x:
3 -5 6 12 21 -7 72 45
x:
3 -5 6 12 21 -7 45 72
x:

21. Bubble Sort - Example
21
3 -5 6 12 21 -7 45 72
x:
Pass: 2
-5 3 6 12 21 -7 45 72
x:
-5 3 6 12 21 -7 45 72
x:
-5 3 6 12 21 -7 45 72
x:
-5 3 6 12 21 -7 45 72
x:
-5 3 6 12 -7 21 45 72
x:
-5 3 6 12 -7 21 45 72
x:

22. Bubble Sort
void bubbleSort (int a[ ] , int size)
{
int i, j, temp;
for ( i = 0; i < size; i++ ) /* controls passes through the list */
{
for ( j = 0; j < size - 1; j++ ) /* performs adjacent comparisons */
{
if ( a[ j ] > a[ j+1 ] ) /* determines if a swap should occur */
{
temp = a[ j ]; /* swap is performed */
a[ j ] = a[ j + 1 ];
a[ j+1 ] = temp;
}
}
}
}

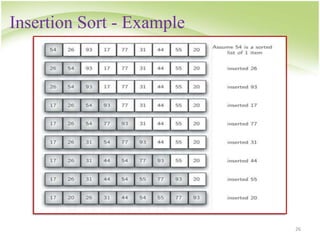
23. Insertion Sort
23
General situation :
0 size-1
i
remainder, unsorted
smallest elements, sorted
0 size-1
i
x:
i
j
Compare and
Shift till x[i] is
larger.

24. Arranging Your Hand
7
5 7

25. Insertion Sort
25
void insertionSort (int list[], int size)
{
int i,j,item;
for (i=1; i<size; i++)
{
item = list[i] ;
/* Move elements of list[0..i-1], that are greater than
item, to one position ahead of their current position */
for (j=i-1; (j>=0)&& (list[j] > item); j--)
list[j+1] = list[j];
list[j+1] = item ;
}
}

26. 26
Insertion Sort - Example

27. Insertion Sort
void insertionSort(int numbers[], int array_size)
{
int i, j, index;
for (i=1; i < array_size; i++) {
index = numbers[i];
j = i;
while ((j > 0) && (numbers[j-1] > index)) {
numbers[j] = numbers[j-1];
j = j - 1;
}
numbers[j] = index;
}
}

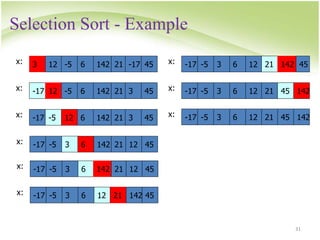
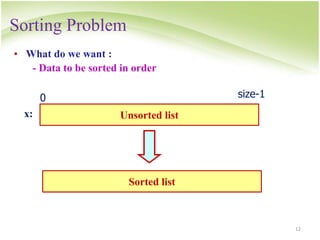
28. Selection Sort
28
General situation :
remainder, unsorted
smallest elements, sorted
0 size-1
k
x:
Steps :
• Find smallest element, mval, in x[k…size-1]
• Swap smallest element with x[k], then increase k.
0 k size-1
mval
swap
x:

29. Selection Sort
29
/* Yield location of smallest element in
x[k .. size-1];*/
int findMinLloc (int x[ ], int k, int size)
{
int j, pos; /* x[pos] is the smallest
element found so far */
pos = k;
for (j=k+1; j<size; j++)
if (x[j] < x[pos])
pos = j;
return pos;
}

30. Selection Sort
30
/* The main sorting function */
/* Sort x[0..size-1] in non-decreasing order */
int selectionSort (int x[], int size)
{ int k, m;
for (k=0; k<size-1; k++)
{
m = findMinLoc(x, k, size);
temp = a[k];
a[k] = a[m];
a[m] = temp;
}
}

31. Selection Sort - Example
31
-17 12 -5 6 142 21 3 45
x:
3 12 -5 6 142 21 -17 45
x:
-17 -5 12 6 142 21 3 45
x:
-17 -5 3 6 142 21 12 45
x:
-17 -5 3 6 142 21 12 45
x:
-17 -5 3 6 12 21 142 45
x:
-17 -5 3 6 12 21 45 142
x:
-17 -5 3 6 21 142 45
x: 12
-17 -5 3 6 12 21 45 142
x:

32. The Time complexity (Average Case) for some
searching and sorting algorithms are listed
below:
• Binary Search: O(log n)
• Linear Search: O(n)
• Bubble Sort: O(n * n)
• Insertion Sort: O(n * n)
• Selection Sort: O(n * n)