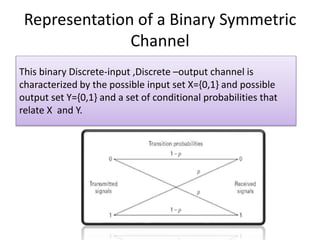
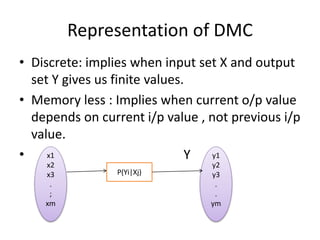
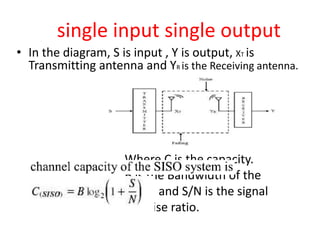
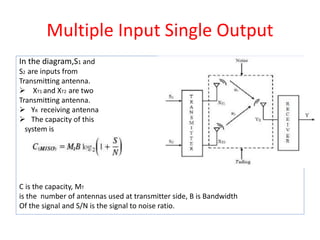
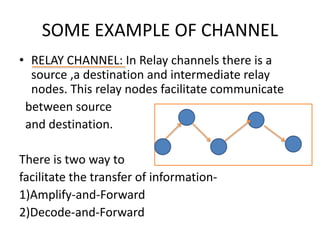
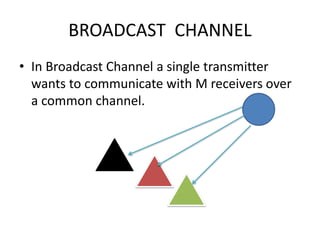
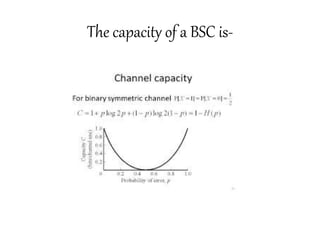
This document introduces channel models and channel capacity. It defines a binary symmetric channel (BSC) as a channel with input and output sets of {0,1} and a crossover probability p that an input bit is flipped. A discrete memoryless channel is characterized by a conditional probability matrix relating discrete inputs to outputs. Channel types include single-input single-output, single-input multiple-output, multiple-input single-output, and multiple-input multiple-output. Channel capacity is the maximum mutual information between input and output, achieved by optimizing the input distribution. Capacity examples include relay channels and multiple access channels. The BSC capacity is 1-H(p) where H(p) is the entropy function

1. INTRODUCTION TO CHANNEL MODEL
AND CHANNEL CAPACITY

2. PRESENTED BY-
SHILPA DE(35000116019)

3. CONTENTS:
•BINARY SYMMETRIC CHANNEL
•DISCRETE MEMORYLESS CHANNEL
•TYPES OF CHANNEL
•EXAMPLES OF CHANNEL
•CHANNEL CAPACITY
•CROSSOVER PROBABILITY

4. BINARY SYMMETRIC CHANNEL

5. Representation of a Binary Symmetric
Channel
This binary Discrete-input ,Discrete –output channel is
characterized by the possible input set X={0,1} and possible
output set Y={0,1} and a set of conditional probabilities that
relate X and Y.

6. • Let the noise in the channel cause independent
errors with average probability of error p.
P(Y=0|X=1) = P(Y=1|X=0) = p
P(Y=1|X=1) = P(Y=0|X=0) = 1-p
A BSC is a special case of Discrete Memoryless
Channel.

7. Representation of DMC
• Discrete: implies when input set X and output
set Y gives us finite values.
• Memory less : Implies when current o/p value
depends on current i/p value , not previous i/p
value.
• X Yx1
x2
x3
.
;
xm
y1
y2
y3
.
.
ym
P(Yi|Xj)

8. DEFINITION OF DMC
• When channel accept a input symbol X, and in
respond generate output symbol Y, this input
and output along with a conditional
probability called DMC.
The conditional probability-
P(Y=yi | X=xj) = P(yi | xj) that characterized a DMC is
arranged in the matrix form called the Probability
transition matrix.

9. TYPE OF CHANNELS:
1)Single Input Single Output (SISO)
2) Single Input Multiple Output (SIMO)
3) Multiple Input Single Output (MISO)
4) Multiple Input Multiple Output (MIMO)

10. single input single output
• In the diagram, S is input , Y is output, XT is
Transmitting antenna and YR is the Receiving antenna.
Where C is the capacity.
B is the Bandwidth of the
signal and S/N is the signal
to noise ratio.

11. • In the diagram, S is input,Y1 and Y2 are two output
from two receiving antenna , XT is transmitting antenna.
• YR1 and YR2 are two
receiving antenna.
• The channel capacity
of the SIMO system
is
Single Input Multiple Output

12. In the diagram,S1 and
S2 are inputs from
Transmitting antenna.
 XT1 and XT2 are two
Transmitting antenna.
 YR receiving antenna
 The capacity of this
system is
C is the capacity, MT
is the number of antennas used at transmitter side, B is Bandwidth
Of the signal and S/N is the signal to noise ratio.
Multiple Input Single Output

13. Multiple Input Multiple Output

14. SOME EXAMPLE OF CHANNEL
• RELAY CHANNEL: In Relay channels there is a
source ,a destination and intermediate relay
nodes. This relay nodes facilitate communicate
between source
and destination.
There is two way to
facilitate the transfer of information-
1)Amplify-and-Forward
2)Decode-and-Forward

15. RELAY CHANNEL
Amplify-and-Forward: Each relay node simply amplifies
the received signal and forward it to the next relay node
, maintaining a fixed average transmit power.
Decode-and-Forward: The relay node can first decode the
received signal and then re-encodes the signal before
forwarding it to the next relay node .

16. MULTIPLE ACCESS CHANNEL
• In Multiple Access Channel, Suppose M
transmitters wants to communicate with a
single receiver over a common channel.

17. BROADCAST CHANNEL
• In Broadcast Channel a single transmitter
wants to communicate with M receivers over
a common channel.

18. CHANNEL CAPACITY:
The channel capacity of a discrete
memoryless channel is defined as-
The maximum average mutual
information in any single use of the
channel,where the maximization is
over all possible input probabilities.

19. C=max I(x;y)
p(xj)
Where average mutual information provided by
the output y about input x is given by-
q-1 r-1
I(x;y)=∑ ∑ p(xj)p(yi|xj) log(yi|xj)/p(yi)
j=0 i=0
where,
P(xj)=input symbol probability
P(yi)=output symbol probability
P(yi|xj)=channel transition probability(determined by channel
characteristics)

20. So,
C=max I(x;y)
p(xj)
q-1 r-1
= max∑ ∑p(xj)p(yi|xj) logp(yi|xj)/p(yi)
j=0 i=0
The maximization of I(x;y) is performed under the constraints
P(xj)>=0 and
q-1
∑p(xj)=1
j=0

21. Units:
• The units of channel capacity is bits/channel
use(where base of logarithm is 2)
• If base of the logarithm is e,the units of
channel capacity will be nats/channel
use(coming from natural logarithm)

22. Crossover probability:
In case of BSC with channel transition
probability p(0|1)=p(1|0)=p
Thus,the transition probability matrix is given by
P= 1-p p
p 1-p
Here,P is reffered to as crossever probability.

23. Now by symmetry,the capacity-
C=max I(x;y)
P(xj)
Is achieved for input probabilities p(0)=p(1)=0.5
So,we obtain the capacity of a BSC as
C=max I(x;y)
=max H(yi)-H(yi|xj)
=1-(+plog(1/p)+(1-p)log(1/1-p))
=1+plogp+(1-p)log(1-p)

24. Let us define the entropy
function,
H(yi|xj)=H(p)=plog(1/p)+(1-p)log(1/1-p)
=-plogp-(1-p)log(1-p)
Hence,we can rewrite the capacity of a binary
symmetric channel as
C=1-H(p)

25. The capacity of a BSC is-

26. Now,from previous equation of
channel capacity-
•For p=0(noise free channel),the capacity is
1bit/channel use.Here we can successfully transmit 1 bit
of information.
For p=0.5,the channel capacity is 0.Output gives no
information about input.it occurs when the channel is
broken.
•For 0.5<p<1,the capacity increases with increasing p.
•For p=1,again channel capacity is 1 bit/channel use.

27. REFFERENCE:
1. INFORMATION THEORY,CODING
AND CRYPTOGRAPHY(RANJAN
BOSE)
2. www.geeksforgeeks.com
3. www.wikepedia.com

28. THANK YOU