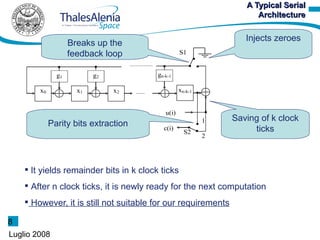
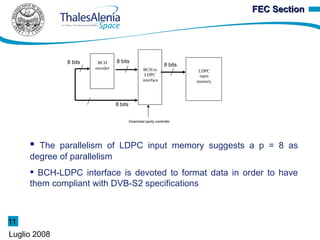
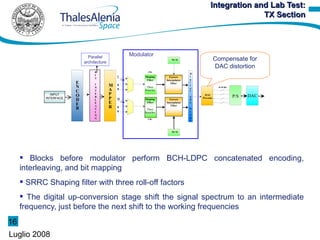
This document discusses the design of a parallel BCH encoder for satellite transmitters. Key points: 1) It proposes a new parallel algorithm for BCH encoding to increase throughput while meeting ASIC requirements for space systems. 2) The algorithm models BCH encoding as a linear system and exploits regularities in the state transition matrix to parallelize encoding. 3) A prototype parallel BCH encoder was designed and integrated with an LDPC encoder. Lab tests showed the modulator achieved low error vector magnitude at transmission rates up to 30 MBaud.

1. POLITECNICO DI TORINO
III ENGINEERING FACULTY
BCH-LDPC Concatenated Coding and High Order
Modulations for Satellite Transmitters
Advisor Co-Advisor
Prof. dr. Roberto Garello Eng. dr. Domenico Giancristofaro
a.a. 2007-2008
1
Luglio 2008

2. Overview
 Analysis of the state of art of modern satellite communication systems
 Study of DVB-S2 outer code (BCH)
 Theoretical, algorithmical, and architectural study of the BCH encoder
 Definition of a new algorithm on a parallel basis in order to increase data throughput
while being compliant with the specific ASIC technology (suitable for space
environment, radiation tolerant, etc.)
 Module integration with LDPC section and Interleaver
 Design and definition of SW modules (C/C++) to validate the parallel algorithm (test
bench for VHDL)
 Lab tests over the entire TX Section.
2
Luglio 2008

3. Principal Operating Scenario within
Satellite Communications
 Multimedia communications provided to wide geographical areas with low population
densisty
 Maritime communications (e.g., Inmarsat) and Radio Navigation Systems (e.g.,
GPS, Galileo)
 Digital TV Broadcasting (e.g, DVB-S, DVB-S2) and broadband internet access
(DVB-S2) for flexible ACM services
 Earth observation and monotoring (e.g., COSMO-SkyMed): high data rate and short
revisit time (LEO), very high data rate required (roughly 1Gbps)
3
Luglio 2008

4. DVB-S2 System and ACM
within Ka Band
Low Protection
32APSK rate 9/10
High Protection
QPSK rate 1/4 S/N
MOD S/N
Bit Mapping • 4 Modulation Format: DEM
QPSK, 8PSK, 16APSK e 32APSK
Interleaver • 11 Code Rates spanning Deinterleaver
ENC-LDPC between 1/4 and 9/10 DEC-LDPC
• Spectral Efficiency η ≈ r∙ log2M
ENC-BCH between 0,5 and 4,5 bit/s/Hz DEC-BCH
4 • S/N ratio from –2dB to +17dB
S D
Luglio 2008

5. Channel Coding for DVB-S2 (BCH-LDPC)
Outer BCH Code
 Primitive shortened
 Three level of protection (8, 10, 12)
 Gives an extra protection against the error floor at higher SNR
Inner LDPC Code
 Performance close to Shannon limit
 Reasonable level of complexity
5
Luglio 2008

6. BCH Encoding Algorithm
1. Multiplication (shift) and zero padding
r
m( x)⋅x Polynomial
2. Remainder computation Generator
r
d ( x)=m( x)⋅x mod g ( x)
3. Remainder bits get appended
d ( x)=m( x)⋅x r mod g ( x)
6
Luglio 2008

7. A Simple HW Architecture
The computation gets
interrupted for k clock ticks
g1 g2 gn-k-1
…un-1un x0 x1 x2 xn-k-1
 This LFSR yields remainder bits in n clock ticks
 This kind of architecture is not going to work seamlessy :
 Parity bits have to be extracted not serially
 Shift register needs to be reset after each computational cycle
7
Luglio 2008

8. A Typical Serial
Architecture
Injects zeroes
Breaks up the
feedback loop S1
g1 g2 gn-k-1
x0 x1 x2 xn-k-1
u(i)
1 Saving of k clock
Parity bits extraction c(i)
S2 ticks
2
 It yields remainder bits in k clock ticks
 After n clock ticks, it is newly ready for the next computation
 However, it is still not suitable for our requirements
8
Luglio 2008

9. Algorithm at Higher Throughput:
Linear System Modeling
[ ] []
State equation
g0 1
g1 0
x (i )=A x (i +1)+b u (i )
b= ⋮ b= 0
⋮ ⋮
g n−k −2 ⋮
[ ]
g n−k −1 0
0 0 … 0 g0
1 0 … 0 g1
Input-state transition
A= ⋮ 1 … 0 g2 vectors
0 ⋮ ⋱ … ⋮
0 0 … 1 g r−1  The state matrix is relevant to
the system itself and so is common
to both system
State transition matrix: It
models its evolution  I-S Vectors change as input
position changes
9
Luglio 2008

10. System Parallelization
By applying the following This matrix shows some sort
recursive substitution of regularity
x (i )=A x (i −1)+b u (i −1)
x (i −1)=A x (i −2)+b u (i together
Putting −2) p
Ap=
( 0 C1
I C2 )
column vectors
p: parallelismo )
(b Ab L A p −1 b It is common to both
system
p−1
x (i )=A x (i −p )+ ∑ A k b u (i −k −1)
p
k =0
Bp= I
0 () LFSR
x (ip)=A p x [(i −1) p ]+B p u (ip)
Bp Serial encoder
10
Luglio 2008

11. FEC Section
8 bits BCH 8 bits
8 bits
encoder BCH to LDPC
LDPC input
interface memory
8 bits
Download parity controller
 The parallelism of LDPC input memory suggests a p = 8 as
degree of parallelism
 BCH-LDPC interface is devoted to format data in order to have
them compliant with DVB-S2 specifications
11
Luglio 2008

12. Parallel BCH Encoder
COMB0 X0 COMB An
1st row
X1 COMB An
2nd row
( )
x 184
COMB1
1 X2 … C 1⋅ ⋮
… x 191
COMB2 … … …
… …
X7 COMB An
… 8th row
p bit
… X8
EXOR x9
COMB An
… 9th row
From COMB8
X9
( )
COMB7 COMB An
x 184
From x175
10th row From COMB
9 … C 2⋅ ⋮
COMB8 To EXOR x9
… x 191
X183 COMB An
… 184th row
… … From x181
… … COMB An
X190
… From x183 191th row From COMB190
X191 COMB An
12 COMB191
192th row
Luglio 2008

13. Combinatorial Networks
Makes the logic ai,183 or ci,1
more adaptable
ai,184 or ci,2
They are suitable …
for each protection …
level ai,191 or ci,8 …
 Each combinatorial network performs a row by column product
 The networks (192) ahead of the state registers performB 8⋅u
( )( )
x
 The ones behind (192) carry out products C 1 ⋅ 184
⋮
C2
x 191
13
Luglio 2008

14. BCH-LDPC Interface
x(184-8*i)
x0 LSB
i=0
x1 .
x2 .
x(184-8*i) . … controller
x3 i=23
T
x(185-8*i)
i=0 o
.
… 8 bits
…
From BCH encoder
. … L
. … D
… x(185-8*i)
i=23 … P
C
… … …
…
i
x(190-8*i)
… i=0
n
p
u
x184 x(190-8*i) t
i=23 8 bits
x185 m
x(191-8*i)
MSB e
… i=0 m
x190 o
r
x191 x(191-8*i) From k y
14 i=23 informative bits
0
Luglio 2008

15. Algorithm Validation
Pseudo random The position of each error is a r.v.
Noise source uniformly distributed between 1 and
n, the block length
Message
Generator
Error source Comp
Decoding section
Error Berlekamp Error
BCH Encoder
Detection Massey Correction
Syndrome
Computation
 Decoding blocks exploit useful precomputed Galois Tables
 Berlekamp-Massey algorithm figures out error polinomial locator coefficients
 Error correction block finds error positions by Chien search
15
Luglio 2008

16. Integration and Lab Test:
TX Section
Parallel Modulator
architecture
NC O Compensate for
DAC distortion
B 3 Rs
D
I
I Shaping Farrow i
T g
7 Bit Filter Interpolator
E Filter i
N
I
N
M 0
Three
t
8-10 B i t
a
C T A 0 Branches l
INPUT O E P DAC
DAC
INTERFACE R
P U P re co m . P/S
D L Q Shaping Farrow P
E E E 7 Bit Filter Interpolator C
Filter
R
A
V
R 0
Three S
I 0 Branches t
N a
G g
3 Rs e
NC O
 Blocks before modulator perform BCH-LDPC concatenated encoding,
interleaving, and bit mapping
 SRRC Shaping filter with three roll-off factors
 The digital up-conversion stage shift the signal spectrum to an intermediate
frequency, just before the next shift to the working frequencies
16
Luglio 2008

17. Setup
Measures EVM, the Error Vector
Module
Stratix II DSP Agilent Infinium MSO Agilent 89600 Vector
development board 6054A Signal Analyzer
 L’FPGA (EP2S180) on
Oscilloscope Software demodulation
board containing the TX
wired to the provides the phase and
Section synthesis
DAC output amplitude error with
 Stratix II development respect to constellation
board has two 14 bit points
(165 Msample/s) DACs
 Generates scatter plots
and measures the signal
17 spectrum
Luglio 2008

18. Modulator Performance
(2 MBaud – 16-APSK)
EVM
Amplitude
2%
Error: 0,9%
 Distance from ideal performance very small
 The DAC distortion, at low transmission rate, is very small
18
Luglio 2008

19. Performance
(30 MBaud – 8-PSK)
EVM
9%
EVM
4%
Without precompensation filter With compensation filter
Precompensation Filter Il DAC causes
flattens the spectrum distortion at high
frequencies since it
cuts them (low pass)
19
Luglio 2008